二阶扰动观测器实现永磁同步电机电流补偿控制

熊少华， 游龙华， 黄宴委

(1. 福州大学电气工程与自动化学院， 福建 福州　350116；2. 龙岩烟草工业有限责任公司， 福建 龙岩　364000)



二阶扰动观测器实现永磁同步电机电流补偿控制

熊少华1， 游龙华2， 黄宴委1

(1. 福州大学电气工程与自动化学院， 福建 福州350116；2. 龙岩烟草工业有限责任公司， 福建 龙岩364000)

摘要：永磁同步电机速度伺服系统的电流环存在外部干扰和系统参数摄动， 影响了PI控制的性能. 利用系统输出与内模输出误差， 设计一种新型的鲁棒内环扰动观测器， 来估计系统不确定量补偿量. 在保证系统鲁棒稳定性条件下， 设计扰动观测器的动态响应为二阶系统， 达到无稳态误差. 实验仿真表明， 增加了扰动观测器补偿的PI电流环控制系统， 能够很好地抑制电流环中的扰动， 减小电流波动， 提高电流的跟踪精度.

关键词：永磁同步电机； 扰动观测器； PI控制； 二阶动态性能

0引言

在速度伺服系统中， 电流环是控制系统的内环， 其性能的好坏， 制约着整个控制系统的性能. 但在实际中， 电流环往往容易受到外部干扰和系统参数摄动的影响， 常规的PI控制， 难以满足高精度的控制要求.

近年来， 系统抗扰动控制， 已成为速度控制中的研究热点， 大量的研究者从事于该领域的研究， 取得了大量的成果， 其中主要的控制策略有自适应控制[1-3]、 滑模变结构控制[4-6]、 神经网络控制[7]、 内模控制[8]以及智能控制等方法. 这些方法主要是针对速度外环的控制， 而对电流环的研究相对较少. 文献[5]设计了一种负载扰动观测器， 补偿负载变化引起的误差， 提高了系统的鲁棒性， 但没有考虑电流环中系统参数摄动和外部干扰， 当系统发生参数摄动和外部干扰时， 速度会出现不良的波动. 文献[8]提出了一种基于内模的滑模电流控制策略， 利用滑模控制鲁棒性强的优点， 采用积分滑模控制， 实现对系统参数摄动和外部干扰的抑制， 该方法提高了系统的鲁棒性， 但在滑模控制趋近段时， 系统鲁棒性无法得到保证.

文献[9-10]在电流环的控制中加入了扰动观测器， 通过观测器识别系统的干扰和参数摄动不确定量， 在线补偿系统的误差， 增强了系统的抗干扰能力， 提高了电流的控制精度， 但是所设计的观测器是误差的一阶系统， 限制了观测器的响应速度， 降低了观测器的性能. 文献[11]提出了一种基于Web的自适应模糊控制方法， 有效地提高了系统的性能， 但是控制策略复杂， 实现起来困难.

本研究在电流环中通过实际系统输出与额定参数模型输出之间的误差函数设计观测器控制律， 使得误差控制系统具有二阶动态特性. 进而用于克服系统参数摄动与外部干扰影响， 完成二阶内环扰动观测器设计， 并推导出了鲁棒内环扰动观测器控制器的结构形式， 分析和证明了系统的鲁棒稳定性. 仿真对比研究表明， 基于该扰动观测器的PI复合控制方法对外部干扰和系统参数摄动有明显的抑制效果.

1永磁同步电机的数学模型

忽略磁场饱和效应、 谐波反电动势、 磁滞及涡流损耗的影响， 磁场呈正弦分布， 则电机在d-q轴坐标系下的数学模型：

(1)

式中：vd，vq分别为d-q轴坐标系下的定子电压；id，iq分别为d-q轴坐标系下的定子电流；R为电机的每一项定子电阻；L为电机的每一项定子电感；φ为永磁磁链；w为电机角速度；np为电机的极对数.

对式(1)进行整理， 可得其状态方程为：

(2)

但在实际中， 永磁同步电机的参数R， L， φ会围绕其标定值Ro， Lo， φo发生变化， 其变化值分别为ΔR， ΔL， Δφ. 定义系统总的不确定量为：

(3)

则实际系统的状态空间方程为：

(4)

2速度伺服系统控制结构

在永磁同步电机速度伺服控制结构中， 采用矢量控制策略， 使直轴电流id=0， 这样控制系统可以等效为直流电机的控制模型， 其整体控制结构如图1所示. 其中电流环采用带有扰动补偿的PI控制方法， 针对在电流环中存在的参数摄动和外部干扰， 设计一种新型二阶扰动观测器， 补偿参数摄动和外部干扰引起的误差， 减小电流的波动， 提高电流的跟踪精度， 增强系统的鲁棒性.

图1中， 永磁同步电机在定向磁场控制策略下， 由速度和电流两环串级控制， 速度环和电流环均采用PI控制器. 由于在电机系统中存在着系统参数摄动和负载扰动等不确定因素， 本研究设计一种电流环观测器， 来补偿电流环PI控制量， 以提高电流跟踪精度.

3扰动观测器

3.1扰动观测器结构形式的推导

图2中虚框为扰动观测器的结构， 可以得到给定输入u和外部干扰d的输入输出关系为：

(5)

假设被控对象的实际模型与标定模型， 具有乘性不确定性， 即：

(6)

则由式(5)可得， 对于名义系统， 其等效扰动为：

(7)

为了实现系统对确定量的补偿和外部扰动的抑制， 则要满足：

(8)

式中，yΔ(s)为等效扰动的输出.

(9)

式中：L≥k且L+M≥N.

证明系统等效扰动输出的稳态值为：

(10)

其中： 当L+1≥k， 即L≥k时yΔ(∞)=0， 则可证明， 按照定理1设计的扰动观测器， 保证系统在稳态时， 能够实现等效扰动的无误差补偿， 系统近似满足式(8).

3.2电流环扰动观测器的设计

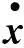
将xb做为扩展状态变量， 则系统的扩展状态方程为：

(11)

在式(11)的基础上， 由扰动观测器的结构， 构造扰动观测器为：

(12)

(13)

则由式(12)和式(13)构造的扰动观测器， 其误差动态方程为：

(14)

3.3永磁同步电机电流内环的鲁棒稳定性分析

由图2可知， 系统的特征方程为：

(15)

定理2带有乘性不确定性的系统如下式所示， 如果pm(s)稳定， 且k(s)和c(s)可以镇定pm(s)， 那么闭环系统鲁棒稳定的充分条件为Δ(s)满足：

(16)

式中：

证明闭环系统的特征方程如下：

(17)

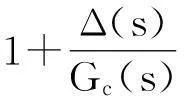
4仿真对比

为验证基于扰动观测器的PI复合控制对外部干扰和系统参数摄动抑制的有效性， 对永磁同步电机的速度伺服控制系统进行了仿真研究， 并与传统PI控制进行了分析比较. 系统的仿真图如图4～6所示.

所用永磁同步电机的参数为： 电枢电阻Ro=13 Ω， 电枢电感Lo=0.032 H， 极对数np=4， 永磁磁链φo=0.119 Wb， 转动惯量J=0.000 3 kg·m2， 转矩系数cm=0.712 N·m， 电机的最高转速为nmax=3 000 r·min-1， 最大限制电流为imax=1.6 A. 仿真时外环速度给定值w*=100 rad·s-1， 负载TL=0.3 N·m， 系统参数变化值ΔR=0.5Roδ1Ω， ΔL=0.2Loδ2H， ΔΦ=0.000 3Φoδ3Wb，εq=εd=0.05δ4V， 其中：δ1，δ2，δ3，δ4为幅值在[-1, 1]之间的随机数， 其频率为1 000 Hz， 电流环PI控制器的参数根据名义系统进行设置， 取无阻尼自然频率wn=1 000 rad·s-1， 考虑到PI控制器零点对阻尼比的影响， 取ε=1.45， 则电流环PI控制器的参数为kp=80，ki=32 000， 同样选取速度PI控制器的参数为kp=0.016，ki=0.004. 为了满足式(11)假设， 要求扰动观测器的响应速度快于参数摄动的响应速度， 则取扰动观测器的无阻尼自然频率wn是参数变化频率的3～4倍， 即取wn=20 000 rad·s-1， 阻尼比ε=0.75.

图4为常规PI控制方法， 图5为带有新型扰动观测器的PI控制方法. 图4(a)， 5(a)反映了在不同控制方法下q轴的电流响应， 在稳态时电流的波动幅值分别为0.05和0.02 A； 图4(b)， 5(b)反映了在不同控制方法下d轴的电流响应， 在稳态时电流的波动幅值分别为0.02和0.01 A. 由仿真对比研究可知， 本研究提出的控制方法， 其电流的波动幅值为常规PI控制方法的一半， 电流环中的扰动得到明显抑制， 提高了内环的跟踪性能. 在电流内环改善的情况下， 速度伺服系统的性能亦得到较好的提高， 如图4(c)， 5(c)所示， 其速度响应在稳态时波动明显较小.

图6反映的是d-q轴不确定量的估计值. 仿真实验表明， 将扰动观测器估计的不确定量， 补偿到系统中， 能够很好地抑制外部干扰和系统参数摄动， 增强系统的鲁棒性， 提高伺服系统的性能.

5结语

针对速度伺服系统的电流内环， 为克服外部干扰和系统参数摄动对系统的影响， 将扰动观测器加入到电流环， 补偿扰动引起的系统误差， 减小电流的波动， 提高电流内环的跟踪性能. 通过改善内环控制， 增强速度伺服系统的鲁棒性， 提高速度伺服系统的性能. 最后， 将所提出的基于新型扰动观测器的PI控制方法与传统的PI控制方法进行仿真比较. 结果表明， 所提出的复合控制方法， 对外部干扰和系统参数摄动， 有明显的抑制效果， 改善了系统的性能， 且相对于其他方法而言， 该复合控制方法简单可行， 容易实现.

参考文献：

[1]鲁文其， 胡育文， 梁骄雁， 等. 永磁同步电机伺服系统抗扰动自适应控制[J]. 中国电机工程学报， 2011， 31(3): 75-81.

[2]JUNG J W, LEU V Q, DO T D,etal. Adaptive PID speed control design for permanent magnet synchronous motor drives[J]. IEEE Transactions on Power Electronics， 2015， 30(2)： 900-908.

[3]蔡满军， 赵成圆. 永磁直线同步电机的自适应迭代学习控制[J]. 微特电机， 2014， 42(6): 48-54.

[4]李政， 胡广大， 崔家瑞， 等. 永磁同步电机调速系统的积分型滑模变结构控制[J]. 中国电机工程学报， 2014， 34(3): 431-437.

[5]刘颖， 周波， 方斯琛. 基于新型扰动观测器的永磁同步电机滑模控制[J]. 中国电机工程学报， 2010， 30(9): 80-85.

[6]张晓光， 孙力， 赵克. 基于负载转矩滑模观测的永磁同步电机滑模控制[J]. 中国电机工程学报， 2012， 32(3): 111-116.

[7]刘贤兴， 胡育文. 永磁同步电机的神经网络逆动态解耦控制[J]. 中国电机工程学报， 2007， 27(27): 72-76.

[8]周华伟， 温旭辉， 赵峰， 等. 基于内模的永磁同步电机滑模电流解耦控制[J]. 中国电机工程学报， 2012， 32(15): 91-99.

[9]KIM K H, MOON G W, YOUN M J,etal. A current control for a permanent magnet synchronous motor with a simple disturbance estimation scheme[J]. IEEE Transactions on Control Systems Technology， 1999， 7(5)： 630-633.

[10]YASSER A, EHAB F. A current control scheme with an adaptive internal model for torque ripple minimization and robust current regulation in PMSM drive systems[J]. IEEE Transactions on Energy Conversion， 2008， 23(1)： 92-100.

[11]ZHOU C, DUC Q, XIONG N,etal. An improved direct adaptive fuzzy controller of uncertain PMSM for web-based E-service systems[J]. IEEE Transactions on Fuzzy Systems， 2015， 23(1)： 58-71.

(责任编辑： 沈芸)

The second-order disturbance observer compensates the current loop of permanent magnet synchronous motor

XIONG Shaohua1， YOU Longhua2， HUANG Yanwei1

(1. College of Electrical Engineering and Automation， Fuzhou University， Fuzhou， Fujian 350116， China;2. Longyan Tobacco Industry Co Ltd， Longyan， Fujian 364000， China)

Abstract:The external disturbances and parameters variations exist in the current loop of the permanent magnet synchronous motor speed servo system, and they deteriorate the PI control performance. Here, robust disturbance observer is proposed by using the output error between the system and the internal model to estimate the system uncertainties. Under the condition of the system robust stability, the proposed observer has a second-order dynamics and no steady-state error. The experimental simulation shows that the PI current control system with the proposed observer compensation can effectively restrain disturbance, reduce current ripple, and improve the tracking precision of the current.

Keywords:permanent magnet synchronous motor; disturbance observer; PI control; second-order dynamics

中图分类号：F407.67

文献标识码：A

基金项目：国家自然科学基金资助项目(51377023)； 教育部博士点新教师科研基金资助项目(20113514120007)； 福建省自然科学基金资助项目(2015J01245)

通讯作者:黄宴委(1976-)， 博士， 副教授， 主要从事非线性电机控制研究， sjtu_huanghao@fzu.edu.cn

收稿日期:2015-04-16

文章编号：1000-2243(2016)02-0225-07

DOI:10.7631/issn.1000-2243.2016.02.0225