基于差分进化的量子密钥分发数据协调优化

王晓凯，阎　金，郭大波，刘绍婷，张　津，蔡　妍

(1. 山西大学 物理电子工程学院，山西 太原 030006； 2. 中北大学 计算机与控制工程学院，山西 太原 030051)



基于差分进化的量子密钥分发数据协调优化

王晓凯1，阎金1，郭大波1，刘绍婷1，张津2，蔡妍2

(1. 山西大学 物理电子工程学院，山西 太原 030006； 2. 中北大学 计算机与控制工程学院，山西 太原 030051)

摘要:针对量子密钥分发中的数据协调技术，引入差分进化算法优化非规则低密度奇偶校验码，并结合高斯近似得到在较大门限值下校验矩阵的度分布. 为了提高搜索效率，避免门限值在进行差分变异时陷入局部最优，引入模拟退火算法重新更新门限值. 通过将优化后的校验矩阵应用于多维密钥分发的数据协调中，能够有效降低收敛信噪比，并且提高数据协调效率. 计算机仿真结果表明： 分组码长为2×105，码率为0.5时，在收敛信噪比SNR=1.15 dB下8维数据协调效率可达90.55%.

关键词:量子密钥分发； 差分进化； 度分布； 模拟退火； 协调效率

随着信息安全技术不断发展，量子保密通信受到人们的普遍关注. 量子保密通信技术利用了传输系统中的量子不可克隆的特性，保证了通信双方在密钥分配过程中能够实现无条件的安全性. 目前，根据光源信号的特征,量子密钥分发技术(Quantum Key Distribution)分为单光子变量和连续变量[1]. 由于单光子光源的制备较为困难，实际实验系统中采用弱脉冲代替单光子，该方法使得通信系统中引入了不安全因素，而且弱脉冲的转化效率较低. 连续变量是利用相干态、 双模纠缠态等高斯量子态作为信号的载波[2]，采用零拍探测技术对光场的相位和振幅进行调制编码从而进行信息传输[3]，而且实际实验装置能够采用经典光信息传输系统，因而具有较高的密钥分发效率和传输距离，引起国内外专家的重视.

在连续变量量子密钥分发(Continuous-Variable-QKD)技术中，当量子高斯态信息由发送端Alice传到接收端Bob后，由于信道噪声的干扰以及第3方的窃听行为，导致通信过程中传递的密钥串存在不一致的序列，因而还需要后处理中数据协调技术纠正不一致的信息序列，才能完成最终的密钥提取[4]. 目前数据协调方案主要采用Assche等人提出的分层纠错协议[5]，并结合Bloch等提出的利用低密度奇偶校验码(LDPC)作为纠错码型[6]. 实际数据协调过程中，通过校验矩阵对光源信息进行压缩编码以及解码，因此LDPC码的性能是影响数据协调效率的重要因素.

通过设计优化LDPC码校验矩阵的度分布和译码门限值能够使其性能接近香农极限. Richardson等人提出一种基于无环图情况下的密度进化理论[7]，并采用密度进化理论计算出基于消息传递译码(BP)下的最佳译码门限值. 由于在计算消息概率密度时复杂度较高，随后Chung等人提出高斯近似分析方案[8]，将信息传递过程中的多维的消息密度计算简化为一维的均值计算，降低了计算复杂度. 差分近化(Differential Evolution)是一种基于群体差异的并行搜索技术[9]，该算法能够克服码参数优化过程中的错误收敛的现象，但是容易陷入局部最优解，导致过早收敛现象的发生.

数据协调效率是制约CVQKD技术发展的瓶颈，本文通过高斯近似分析LDPC码的门限值，同时为了解决差分进化过早收敛问题，推导出基于模拟退火的优化算法. 在改进的差分进化算法的基础上，对不同码率下的LDPC码校验矩阵度分布进行优化设计. 在多维连续变量量子密钥分发实验中，采用经过优化处理的校验矩阵，能够降低数据协调的收敛信噪比，并提高数据协调效率，实现安全可靠的密钥提取.

1数据协调技术

在量子密钥分发的过程中，接收信息的Bob一方要从发送信息的Alice一方收到可靠信息序列. 实际的通信过程中，由于传输介质的性质、 信道的噪声干扰，损失以及第3方的窃听，导致通信双方获得的信息序列仍存在一定的误码率. 数据协调技术通过接受方Bob在对发送端Alice的原始数据进行量子测量后得到经典信息，并利用公共的经典信道对接受的信息进行协调、 纠错.

图1　基于BB84协议的数据协调模型图Fig.1　The model of data reconciliation based on BB84 protocol

通信双方Alice和Bob基于BB84协议的规定进行信息的交换[10]. 相关的数据协调采用LDPC码为纠错码型，并结合校验子(Syndrome)的压缩编码方案对数据进行处理. 其数据协调模型如图1 所示.

具体的协调步骤如下：

Step 1发送端Alice将原始的密钥数据X经过相干调制后，通过量子信道发送给接受端Bob.

Step 2接受端Bob经过量化编码方法将连续信息Y转化成二进制序列Y′，并通过信道编码方法生成校验矩阵H, 根据H计算得到校验子S=Y′HT. 此时Bob将校验子S通过经典信道返回给Alice端.

Step3Alice端将原有的边信息结合上一步得到的校验子S，采用对数似然比LLR-BP算法进行迭代译码，最终恢复Bob端的二进制序列Y′.

2基于高斯近似优化门限值

2.1高斯近似

(1)

校验节点信息更新表示为

(2)

(3)

(4)

式中：mu0为初始变量消息的均值. 在第l次消息迭代校验节点消息均值表示为

(5)

式中：φ(x) 函数定义为

(6)

图2　非规则LDPC码高斯近似流程图Fig.2　The flow chart of Irregular LDPC codes Gaussian approximation

(7)

(8)

根据式(3)，在第l次消息迭代时，度数为i的变量节点的均值表示为

(9)

度数为j的校验点消息输出均值可以表示为

(10)

由于校验节点所接受的消息密度为

(11)

代入式(10)可得校验节点的消息均值更新

(12)

将式(12)代入式(9)就能得到非规则LDPC码在高斯近似下的概率消息迭代公式. 图2 为非规则LDPC码在AWGN信道下的高斯近似流程图.

2.2门限值计算

1) 初始化参数. 设定信道参数δ初始值，变化步长Δδ，最大迭代次数lmax，并设定目标错误概率Pe以及非规则LDPC的度数分布.

3) 停止迭代. 当达到最大迭代次数时停止迭代并输出门限值δ*=δ-Δδ.

3基于差分进化的码参数优化算法

非规则LDPC码在给定码率下，不同码的度分布在设定目标错误概率和迭代次数的情况下，所计算得到的信道门限值都不同. 因此需要对码的度分布进行设计，使所求得信道门限值达到最大，此时得到的码型为最优码型. 而差分进化算法能够通过随机初始化一个样本序列，并借助进化算子对最优度数分布进行搜索[14]. 传统的差分进化算法通过群体样本的差分矢量来修正个体值，然而在后期收敛时容易陷入局部最优，使得算法过早收敛. 本文在传统差分进化算法中加入模拟退火算法，使得优化后算法能够跳出局部最优. 设序列L表示度分布中自由参数，因此最大门限的度分布优化转化为优化的一个L维向量p=(λi,…,λdv,ρj,…,ρdc). 具体算法步骤描述如下：

1) 初始化

2) 差分进化

经过G+1迭代后，在样本序列[0,NP-1]中随机选取4个样本值r1,r2,r3,r4, 组成新的向量

(13)

3) 模拟退火

Step1： 设定初始温度T0，迭代次数以及退火速率α(0<α<1)，将上述得到的最佳门限pbest,G+1设为初始值.

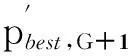
(14)

式中： f(x)为适应函数； ηGuass服从N(0,δ′)的高斯分布.

4) 停止准则

当计算得到的门限值满足δ*>δ，则输出度数分布矢量p=(λi,…,λdv,ρj,…,ρdc)，则返回第2步继续迭代搜索. 经过上述的有限次的迭代，门限值的解空间差异性缩小. 对于每次搜索到接近最优门限值时，继续迭代计算得到门限值变化不大，因此通过门限值比较可以及时跳出循环，减小计算量.

经过上述计算筛选出的值为高斯信道下的最佳门限值的度分布(λ,ρ). 在模拟退火更新最佳门限值时，需要保证在其领域中产生新值，因此需要引入高斯变异的波动方差值δ′来控制，从而避免新产生的门限值过度偏离原值. 根据相应的约束条件，本文取δ′=0.2.

4数值仿真结果及分析

4.1校验矩阵度分布优化

选择码率分别为0.5，0.6和0.7在最大变量节点度数dv分别为4, 6, 8, 10, 20时采用改进的差分进化方法所得到的度分布值，并利用高斯近似计算其门限值. 在AWGN信道下,最大迭代次数为100，通过比较门限值的大小得出度数分布及相应门限值如表1～表3.

表1　码率为0.5的码参数

表2　码率为0.6的码参数

表3　码率为0.7的码参数

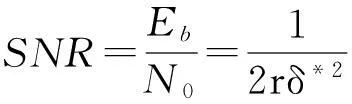
4.2量子密钥分发数据协调优化

本文采用连续变量量子密钥多维数据数据协调算法[15]，通过差分进化的优化方法，结合高斯近似门限值的分析，对LDPC码的校验矩阵H的度数分布进一步优化. 本文采用的仿真硬件实验平台基于CPU为InterXeonE5620 2.4GHz和32G内存的双核服务器，LDPC码度分布分别采用表1～表3 中的第5组实验数据. 码长选用2×105，最大迭代次数为100，共100个分组进行统计实验.

为了便于比较，选用文献[13]中对应码率下的相应数据. 表4 给出了与文献[13]数据协调方案一致情况下，LDPC码的性能与协调效率的比较. 数据协调效率定义的公式[16]为

(15)

表4　数据协调方案的实验结果比较

在码率为0.5的情况下，本文所采用的方案在4维、 8维数据协调时的收敛信噪比RSN为1.32和1.15，比文献[13]中相同实验条件下的收敛信噪比降低了12.0%和4.1%，而且协调效率分别提高了8.9% 和3.0%. 在码率为0.6的情况下，本文实验采用的方案中收敛信噪比比文献中降低了11.8%和7.6%，而协调效率分别提高了7.9%和5.2%. 当码率增加到0.7的时，本文采用的实验方案比文献中实验的收敛信噪比SSN分别降低了1.9%和1.7%，而协调效率分别增加了1.1%和1.0%. 随着码率的增加，3种方案下的收敛信噪比以及协调效率的差距逐渐缩小，根据置信息传递规律码率越高校验节点数越少，而此时校验矩阵可优化的空间也就越小. 较低的收敛信噪比，能够保证密钥在一定误码率的情况下安全传输，因此优化后的协调方案抵御噪声能力增强，延长了光纤通信的距离.

5结论

本文针对量子密钥分发中的数据协调，提出一种改进的差分进化算法,用于优化校验矩阵并结合高斯近似得到了较大门限值下的度数分布. 通过实验仿真表明，优化后的校验矩阵H在4维数据协调和8维数据协调中能够有效降低收敛信噪比，提高协调效率，而且在8维数据协调中，本文采用实验方案信噪比能够降至1.15dB，最大协调效率可达90.55%，对实际量子密钥分发实验具有指导意义.

进一步的研究工作是如何保证低信噪比下的数据吞吐量，以及设计校验矩阵结构更为复杂的多边类型LDPC码的数据协调技术.

参考文献：

[1]王怀胜，杨杰. 连续变量量子保密通信技术[J]. 信息安全与通信保密，2015(7)： 86-91.

Wang Huaisheng，Yang Jie. Continuous variable quantum private communication technology[J]. Information Security and Communications Privacy，2015. (7)： 86-91. (in Chinese)

[2]陈进建，韩正甫，赵义博，等. 平衡零拍测量对连续变量量子密钥分配的影响[J]. 物理学报，2007，56 (1)： 5-9.

Chen Jinjian，Han Zhengfu，Zhao Yibo, et al. The effect of balanced homodyne detection on continuous variable quantum key distribution[J]. Acta Physica Sinica，2007，56 (1)： 5-9. (in Chinese)

[3]Bennett C H，Brassard G. Quantum cryptography： Public key distribution and coin tossing[J]. Theoretical Computer Science，2014，560： 7-11.

[4]孙艺，王晓凯，郭大波，等. 基于粒子群的数据协调优化算法[J]. 测试技术学报，2015，29 (2)： 149-157.

Sun Yi，Wang Xiaokai，Guo Dabo ，et al. The optimized algorithm for data reconciliation based on particle swarm optimzation.[J]. Journal of Test and Measurement Technology，2015，29 (2)： 149-157. (in Chinese)

[5]Van G A，Cardinal J ，Cerf N J. Reconciliation of a quantum-distributed Gaussian key[J]. Information Theory，IEEE Transactions on，2004，50 (2)： 394-400.

[6]Bloch M，Thangaraj A，McLaughlin W S，et.al. LDPC-based secret key agreement over the gaussian wiretap channel[C] .Information Theory，2006 IEEE International Symposium on. IEEE，2006: 1179-1183.

[7]Richardson T J，Urbanke R L. The capacity of low-density parity-check codes under message-passing decoding[J]. Information Theory，IEEE Transactions on，2001，47 (2)： 599-618.

[8]Chung S Y，Richardson T J，Urbanke R L. Analysis of sum-product decoding of low-density parity-check codes using a Gaussian approximation[J]. Information Theory，IEEE Transactions on，2001，47 (2)： 657-670.

[9]杨启文，蔡亮，薛云灿. 差分进化算法综述[J]. 模式识别与人工智能，2008，21 (4)： 506-513.

Yang Qiwen，Cai Liang，Xue Yuncan. A survey of differential evolution algorithms[J]. Pattern Recognition and Artificial Intelligence，2008，21 (4)： 506-513. (in Chinese)

[10]Shor P W，Preskill J. Simple proof of security of the BB84 quantum key distribution protocol[J]. Physical review letters，2000，85 (2)： 441-449.

[11]Chen Jinghu，Fossorier M P. Density evolution for two improved BP-based decoding algorithms of LDPC codes[J]. Communications Letters，IEEE，2002，6 (5)： 208-210.

[12]Lehmann F，Maggio G M. Analysis of the iterative decoding of LDPC and product codes using the Gaussian approximation[J]. Information Theory，IEEE Transactions on，2003，49 (11)： 2993-3000.

[13]袁东风，张海刚. LDPC码理论与应用[M]. 北京： 人民邮电出版社，2008.

[14]刘庆华，刘晓琳，陈紫强. 基于差分进化的非规则 LDPC 码优化设计[J]. 计算机工程，2012，38 (2)： 267-269.

Liu Qinghua，Liu Xiaolin，Chen Ziqiang. Optimal design of irregular LDPC code based on differential evolution[J]. Computer Engineering，2012，38 (2)： 267-269. (in Chinese)

[15]王云艳，郭大波，张彦煌，等. 连续变量量子密钥分发多维数据协调算法[J]. 光学学报，2014(8)： 289-295.

Wang Yunyan，Guo Dabo，Zhang Yanhuang, et.al. Algorithm of multidimensional reconciliation for continuous-variable quantum key distribution[J].Acta Optica Sinica，2014(8)： 289-295. (in Chinese)

[16]Leverrier A，Grangier P. Continuous-variable quantum-key-distribution protocols with a non-Gaussian modulation[J]. Physical Review A，2011，83 (4)： 042312-042319.

The Optimized Algorithm of Data Reconciliation for Quantum Key Distribution Based on Differential Evolution

WANG Xiaokai1, YAN Jin1, GUO Dabo1, LIU Shaoting1, ZHANG Jin2, CAI Yan2

(1. College of Physics and Electronic Engineering, Shanxi University, Taiyuan 030006, China；2. School of Computer Science and Control Engineering, North University of China, Taiyuan 030051, China)

Abstract:In allusion to the data reconciliation technology of quantum key distribution, differential evolution algorithm is proposed to optimize the irregular low-density parity check code ，and under larger threshold with Gaussian approximation the degree distribution is calculated. In order to improve the search efficiency and avoid the threshold falling into local optimum with differential mutating, simulated annealing algorithm is proposed to optimize the threshold. The optimized parity check matrix applies to multidimensional reconciliation which reduces convergence of signal to noise ratio and improve reconciliation efficiency.Simulation results indicate that the eight-dimensional data reconciliation efficiency is up to 90.55% under the convergence SNR=1.15 dB which the length of code is 2×105 and code rate is 0.5 .

Key words:quantum key distribution; differential evolution; degree distribution; simulated annealing; reconciliation efficiency

中图分类号:TN309

文献标识码:A

doi:10.3969/j.issn.1671-7449.2016.02.009

作者简介：王晓凯(1963-)，男，教授，博士，主要从事通信网络管理、 控制与优化等研究.

基金项目：山西省国际科技合作计划资助项目(2014081027-1)； 山西省基础研究资助项目(2014011007-2)； 山西省回国留学人员科研资助项目(2014-012)

收稿日期:2015-09-12

文章编号:1671-7449(2016)02-0142-07