基于爆炸振动波的黄土中空腔坑定位研究

陶　钢，徐利娜，陈化良，任保祥，庞春桥

(1. 南京理工大学 能源与动力工程学院，江苏 南京 210094； 2. 中国兵器工业试验测试研究院，714200)



基于爆炸振动波的黄土中空腔坑定位研究

陶钢1，徐利娜2，陈化良2，任保祥1，庞春桥1

(1. 南京理工大学 能源与动力工程学院，江苏 南京 210094； 2. 中国兵器工业试验测试研究院，714200)

摘要:靶场地下常会有弹坑或弹道坑等，有时需要对它们的位置进行判断，但实际中并没有很好的办法来解决这个问题. 由于土壤介质的复杂性和多样性，很难有统一的方法来预测其位置，特别是土壤的静态和动态力学参数，只能针对具体的土壤去分析. 本文针对我国渭河滩黄土土壤，通过试验研究爆炸波引起的黄土土壤爆炸坑洞的形成和振动传播规律测量，结合土中爆炸力学的理论分析结果，给出黄土土壤中一些爆炸作用的特征参数的估算方法和爆炸或弹道坑空腔的定位方法.

关键词:土中空腔； 爆炸； 土中振动波； 弹道坑空腔定位

0引言

炸药装药在土中爆炸会产生空腔，一些侵彻弹钻入土壤中，也会形成弹坑或弹道空腔坑. 这些空腔中会有未爆弹丸，给靶场带来安全隐患. 有时需要对它们的位置进行判断，因此，如何准确确定这些空腔位置就成为一个需要解决的问题. 由于土中弹道和土壤介质的复杂性和多样性，故很难有统一的方法来预测其位置，特别是所需的土壤静态和动态力学参数，只能针对特定的土壤去研究[1,2]，并给出分析方法. 本文针对我国渭河滩黄土土壤，研究爆炸引起的土壤振动波传播规律，给出一种弹道坑定位方法，以便为其他相关工作提供参考依据.

1试验方案

1.1试验场地状况

本试验在渭河河漫滩阶地进行，该土壤属于黄土壤[3]. 渭河一级阶地土壤(Q4)由亚砂、 亚粘土、 砂砾石层等冲积物组成. 试验场地土壤均匀，射弹穿入土壤后，都会形成一个坑道和空腔. 图1 为本试验TNT药柱，图2 为爆炸后形成的炸坑，直径约D=1.3 m.

图1　试验TNT炸药柱Fig.1　TNT explosive column

图2　爆炸坑，其直径尺寸约1.3 mFig.2　Diameter of explosion crater is 1.3 m

1.2试验布设及测试设备

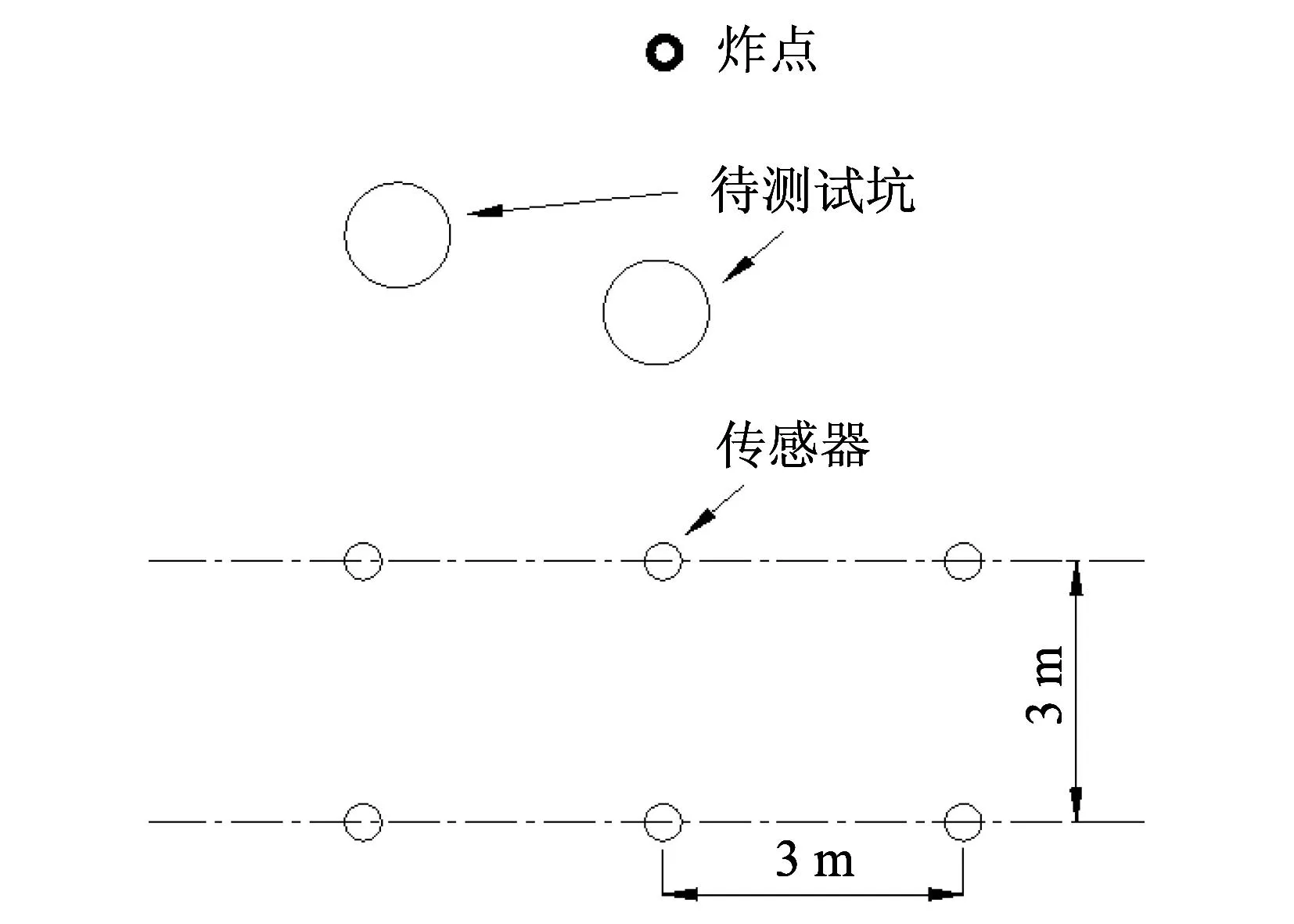
爆炸测试场地布置见图3. 表1 为三向速度传感器编号及布置的距离参数. 图4 为三向速度传感器，上面分别标有X,Y,Z方向，传感器量程： 0.001～ 35.5 cm/s，频率范围5～500 Hz，精度±5%，采样率最大50 kSps.

图3　爆炸点和三轴速度传感器布设图Fig.3　The explosion point and three-axis velocity sensor layout

图4　三向速度传感器Fig.4　The three-axis velocity sensor

序号传感器编号及距离/m1#2#3#炸点12.86425.85248.8764炸点25.37948.364711.3879炸点32.56425.22008.1323炸点45.25028.033210.9719

2试验结果分析

2.1三轴传感器X方向振动波分析

3个三轴传感器的X方向正对炸点1源点，即沿炸点1的爆炸波径向传播方向，见图3. 该方向波为纵波. 下面按照布置的炸点顺序分析X方向的振动波传播规律.

爆炸点1：3个三向传感器测试的速度振动波曲线见图5，传感器布置见图3. 由曲线特征可看到，3个传感器离震源距离由近到远，振幅信号由高到低衰减.

由振动波曲线读取第一波峰值参数，结果见表2. 3个不同位置的峰值衰减特征符合指数衰减规律，如式(1)

(1)

式中：u为振动速度(m/s);kc为系数；r为传感器到震源的距离(m)；m为炸药TNT当量(kg)；α为衰减指数，不同的土壤及状况具有不一样的指数. 拟合曲线见图6，拟合参数为kc=1.9，α=3.3.

表2　 3个记录曲线的第一峰值数据

图5　X方向纵波(P)振幅随距离的变化曲线Fig.5　Curve of X axial p-wave amplitude corresponding to distance

图6　X方向振动波第一峰值的拟合曲线Fig.6　Fitting curves of the first peak of X axial vibration wave

爆炸点2：同样，3个三向传感器测试得到的X方向速度振动波数据曲线见图7，传感器布置见图3.

图7　炸点 2 的X方向纵波振幅随距离的变化曲线Fig.7　Curve of the second burst point’s X axial p-wave amplitude corresponding to distance

图8　炸点2的X方向振动波第一峰值的拟合曲线Fig.8　Fitting curves of the first peak of the fourth burst point’s X axial vibration wave

表3为3个数据信号的第一峰值数据. 这里，1#传感器的第一峰值比炸点1的对应数值小很多，其绝对值小近1个数量级. 这说明炸点1产生的爆炸空腔坑对爆炸点2的X方向振动波传播产生了很大的影响，造成了第一峰值的大幅下降. 同样，对读取的表3数据进行拟合，曲线见图8，拟合参数kc=1.5，α=3.3. 由该拟合曲线可发现，炸点1产生的空腔炸坑主要对1#传感器测点的数据产生影响，而对离土壤中空腔距离稍远的后面两个测点(2#和3#)的第一峰值数据影响并不大，甚至可以忽略. 可知，该坑尺寸对X方向纵波传播的影响距离范围是有限的.

表3　X方向振动曲线的第一峰值数据

爆炸点4：传感器测试的X方向速度振动波结果见图9. 由图3可知，该炸点在爆炸点1的侧面，因此对爆炸点径向传播信号不会产生影响.

表4 为图9 中3个传感器信号的第一峰值数据. 由这些数据可知，炸点1产生的坑对第一峰值没有造成影响，拟合曲线见图10，拟合参数基本符合kc=1.5，α=3.3. 拟合曲线的部分微小偏差是由于传感器测点的X方向偏离炸点径向方向造成的.

表4　3个传感器的第一峰值数据

图9　炸点4的X方向纵波振幅随距离的变化曲线Fig.9　Curve of the fourth burst point’s X axial p-wave amplitude corresponding to distance

图10　炸点4的X方向振动波第一峰值的拟合曲线Fig.10　Fitting curves of the first peak of the fourth burst point’s X axial vibration wave

对上面3个炸点的振动数据分析可知，X方向振动波的第一峰值随距离的衰减规律是一样的，均符合力学指数衰减规律，指数α=3.3. 但当在爆炸点的径向方向存在炸坑时，在离爆炸坑空腔一定距离范围内，会对传感器测量的第一峰值产生很大影响，甚至达到1个数量级，所以需要对这个问题进行分析，找出降低的原因.

2.2弹坑对三轴传感器X方向振动波衍射的效果分析

由上面的分析已知，炸点X方向振动波主要为纵波. 它沿径向向外传播，当遇到前面的坑时，会产生绕射，并在空腔后汇聚，形成交汇作用波. 对于土壤中的交汇波问题，几乎没有可借鉴的研究成果. 由于土壤介质的力学复杂性，很难得到统一的计算方法，只能借鉴一些在介质中传播的相关力学理论进行验证. 为此，我们利用波的非正规反射规律对该图像进行建模分析[4].

图11假设纵波从爆炸源点开始传播，到达坑边缘后，在坑后面发生衍射，并重新汇合并形成新的波. 根据物理知识，当这个汇聚波传播距离r远大于弹坑直径2H时，弹坑的影响将会逐渐消失，因此存在临界距离，所以关键是要求出这个临界距离.本研究所针对的爆炸波传播问题，属于较近距离的爆炸强振动波传播问题，即近场问题，属于强振动波的衍射传播问题. 为此，可以假设，该问题为在坑后面沿对称轴对称运动的两个波的作用问题，并且在对称轴上会产生非正规波作用效应. 于是，可根据相关理论，研究这种作用过程并建立相应的分析模型.

图11　爆炸波经弹坑形成衍射Fig.11　The explosion wave forms diffraction by the crater

图11为假设的波传播模型，图11中爆炸波经弹坑形成衍射，球坑的半径为H，根据强波在对称轴上作用产生的非正规马赫反射公式[4]，有

(2)

式中：H为坑半径(m)；z为马赫三波点离对称轴的距离;r为从坑中心到三波点在对称轴上投影的距离;α*为临界入射角，此处α*=2/9π. 在两个干扰波作用下，z值达到H时，就可认为坑的影响达到终止，也就是说，此时可认为马赫波追上入射冲击波，合并为一个冲击波，其波参数接近无坑的状况，见图11，因此就可以求解出临界值rk. 由式(2)求出

(3)

即： 所求出的临界距离rk离坑中心的距离为3.6H. 作为验证实例，根据已知试验数据，爆炸弹坑直径D=1.3 m，即H=D/2=0.65 m，2#测点离坑中心的距离R=8.364 7 m-5.852 4 m=2.51 m，也就是说，X波传播到坑中心后2.51 m时，其波强度几乎不再受该尺寸坑的影响，于是将该值R=2.51 m，代入式(3)，则得到坑的临界距离rk=3.6H=2.34 m

2.3爆炸炸点传播的X方向波的方位判断

在实际试验测试问题中，判断未知炸点方位是非常必要的. 它可通过三轴传感器的Y方向波来判断爆炸振动波的方位.

取爆炸点2和爆炸点4的Y方向振动波，来分析是否可给出爆炸点的方位.

2#传感器Y方向振动波如图12 所示. 4#传感器Y方向振动波如图13 所示.

图12　爆炸点2的Y方向2#和3#传感器记录的爆炸波曲线Fig.12　The second burst point’s explosion wave curve of 2# and 3# sensors on Y axis

图13　爆炸点4的Y方向2#和3#传感器记录的爆炸波曲线Fig.13　The fourth burst point’s explosion wave curve of 2# and 3# sensors on Y axis

图14　三轴传感器的一种定位布设测试方式Fig.14　A positioning test layout of three-axis sensors

显然，两个传感器记录的爆炸点2和爆炸点4的振动曲线中，第一峰正好符号相反，2#为正，4#为负. 根据实验布设图3，可知正好两个爆炸点处于传感器X方向的两侧. 这个区别在Y方向记录数据上非常明显. 由此可知，根据Y方向记录数据第一峰值的正负号，很容易判断爆炸点的方位.

2.4一种三轴传感器的布置和定位测试方法

本研究的目的是为了给出靶场爆炸点和地下炸坑空腔的位置信息. 根据上面的试验和研究结果，可知只需布置2排相互间隔3 m的三轴传感器，通过小型爆炸(<2 kg TNT) 就可确定土壤中空腔的大小和位置，甚至可以判断弹丸入射产生弹道空腔的位置，见图14.

3结论

本文通过试验和理论分析，得到黄土河漫滩上的爆炸振动波传播的相关知识，得到以下结论：

1) 土壤中的空腔坑对纵波X方向靠近坑背面振动波的影响比较大，该震动波可以作为坑道定位的有效信息；

2) 利用强绕射波的干扰原理，建立纵波绕射坑空腔模型，并求出坑影响的临界距离rk=3.6H. 通过本试验3个传感器振动试验数据，估算出爆炸坑大小尺寸范围，该计算结果与实际坑尺寸非常接近，误差仅为7%. 因此，该方法可以作为类似问题分析和计算的参考；

3) 通过三轴传感器的Y方向信号，可判断爆炸点传播的方位；

4) 给出了一种测试爆炸坑尺寸和定位爆炸点方位的方法.

参考文献：

[1]奥尔连科. 爆炸物理学[M]. 孙承纬, 译. 原书第三版. 北京: 科学出版社, 2011.

[2]Замышляев Б В, Евтерев Л С. Модели динамического деформирования и разрушения грунтовых сред., - М. Наука, 1990. - 215 с.

[3]谢定义. 黄土力学特性与应用研究的过去、 现在与未来[J]. 地下空间，1999, 19(4): 273-284.

Xie Dingyi. The past, present and future of the research on mechanical characteristics and application of loess [J]. Underground Space, 1999, 19(4): 273-284.(in Chinese)

[4]Балаганский И А, Мержневский Л А. Действие средств поражения и боеприпасов-. Учебник. -Новосибирск: Изд-во НГТУ.-2004.-408 с. - (Серия Учебники НГТУ).

[5]赵丽娅，鞠兴华，刘保键，等. 不同含水率下非饱和黄土K0固结特性试验[J]. 南水被调与水利科技, 2012, 10(2): 120-123.

Zhao Liya, Ju Xinghua, Liu Baojian, et al. Analysis on theK0consolidation tests of unsaturated loess under different moisture contents[J]. South-to-North Water Diversion and Water Science & Technology, 2012, 10(2): 120-123. (in Chinese)

[6] 冯志焱，邱本胜，谢定义. 黄土的三轴试验研究[J]. 西安建筑科技大学学报，2010, 42(6): 803-808.

Feng Zhiyan, Qiu Bensheng, Xie Dingyi. Experimental study of triaxial test of loess[J]. Journal of Xi′an University of Architecture & Technology (Natural Science Edition), 2010, 42(6): 803-808. (in Chinese)

Study on Explosion Vibration Wave on the Positioning Cavity in Yellow Soil

TAO Gang1, XU Lina2, CHEN Hualiang2, REN Baoxiang1, PANG Chunqiao1

(1. College of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, China;2. China Weapon Industrial Test Research Institute, 714200, China)

Abstract:The underground of the proving ground often has craters or ballistic holes, sometimes it is need to judge their positions. But in reality there is not a very good way to solve this problem. Because of the complexity and diversity of the soil medium, it is difficult to have a unified method to predict the position, especially the soil static and dynamic mechanical parameters in using, and only the specific soil can be analysed. A method to positioning the explosion or ballistic pit cavity location through experimental study on the propagation law of explosion vibration wave in view of our country Weihe beach yellow soil in this paper.

Key words:cavity in soil; explosion; the vibration wave in soil; positioning localization of ballistic pit cavity

中图分类号:TJ011+.1

文献标识码:A

doi:10.3969/j.issn.1671-7449.2016.02.001

作者简介：陶钢(1962-)，研究员，博士生导师，主要从事终点弹道与毁伤的研究.

基金项目：国防基础基金资助项目(A0920133008)

收稿日期:2015-09-23

文章编号:1671-7449(2016)02-0093-06