岩石单裂纹扩展及损伤演化规律的数值模拟研究
2016-05-25刘丰铭田加深
赵 程,刘丰铭,杨 磊,田加深
(1. 同济大学 地下建筑与工程系,上海 200092;2. 同济大学 岩土与地下工程教育部重点实验室,上海 200092;3. 山东大学 土建与水利学院,山东 济南 250061)
岩石单裂纹扩展及损伤演化规律的数值模拟研究
赵 程1,2,刘丰铭1,2,杨 磊3,田加深1
(1. 同济大学 地下建筑与工程系,上海 200092;2. 同济大学 岩土与地下工程教育部重点实验室,上海 200092;3. 山东大学 土建与水利学院,山东 济南 250061)
采用扩展离散元(EDEM)计算方法,模拟了单轴压缩下含不同预置倾角的单裂纹岩石试样的裂纹起裂、扩展和贯通过程,探讨了裂纹不同扩展阶段的应力变化,分析了不同预置倾角下单裂纹的扩展机制。研究表明:随着预置裂纹倾角α的增大,新裂纹的起裂应力和试样的抗压强度总体上呈增大趋势,但当α=30°时出现突变;α=30°时试样裂纹扩展最为迅速,α=15°,45°,60°,75°时的试样扩展速度依次减弱;当α=15°,30°时,新裂纹从预置裂纹尖端的两翼开始扩展,当α从45°增大到75°时,新裂纹的扩展逐渐向着预置裂纹两侧纵深发展,α=45°时为两种不同裂纹扩展模式的过渡倾角。
隧道工程;岩土工程;扩展离散元(EDEM);数值模拟;岩石材料;单裂纹
0 引 言
一方面,岩石内部存在着大量随机分布的微裂纹,其裂纹的起裂、扩展和贯通的损伤演化过程,是岩石宏观破坏的主要原因之一。另一方面,作为一种常用的土木工程材料,岩石是隧道、矿山和地下空间等大型工程开发利用的主要原材料和研究对象。因此,研究岩石内部裂纹的起裂、扩展和贯通机制,对于揭示岩石的破坏机理和指导工程实践都具有重要的实际应用价值。
对岩石等脆性材料裂纹的扩展及损伤演化规律的研究,主要有实验、理论和数值模拟等方法。就数值模拟研究方面,目前主要有有限元法、无网格法和离散元法等。有限元法在解决复杂力学问题上具有较大地灵活性,如岩石材料的非均匀性、非线性变形和复杂应力条件等问题。T. BELYTSCHKO等[1],N. SUKUMAR等[2],H. PATHAK等[3],P. BROUMAND等[4]和Y. L. ZHANG等[5]均利用有限元对岩石的裂纹扩展做了相应的研究,并取得了丰硕的成果。但有限元法是建立在连续介质假设的基础上的,对于解决非连续介质的问题存在着一定的局限性。无网格法由T. BELYTSCHKO等[6]提出,该方法只需节点信息而无需单元,这就突破了有限元中的网格限制。P. KRYSl等[7],B. N. RAO等[8]人均运用无网格法对岩石裂纹的动态断裂过程进行了模拟,效果较为理想。但无网格法在确定形函数系数中存在繁重不堪的求逆矩阵,造成计算量很大的问题,边界处理也存在较大困难。离散单元法是目前应用于岩石结构分析中最广泛且有效的非连续介质力学数值方法,最早是由P. A. CUNDALL[9]提出应用于不连续岩体的数值求解方法。离散单元法可以计算岩石块体内部的应力和变形,同时又可以分析岩石不同块体接触面的分离、滑移与倾覆旋转,使其能够更真实地模拟节理岩体的几何变形特征。该法实用于解决大变形及开裂的特点,使得其可以更好地模拟节理岩体在荷载作用下的变形情况。离散单元法将节理、裂隙、断层等构造面与不同材料分区的界面作为块体的边界,不同块体用法向与切向弹簧连接,应用牛顿运动定律根据动态松弛法求解系统的运动。相比较而言,离散元还不需要较为复杂的本构关系,且可以从微观到宏观对破坏过程进行分析。所以,国内外许多学者采用离散单元法来模拟岩石裂纹的扩展过程,分析岩石的破裂机理。由块体离散元理论引申出的扩展离散元(EDEM)[10-11]和颗粒体离散元方法(PFC)[12-13]被广泛使用,并通过与室内试验资料相对比验证了该方法模拟岩石的可行性。
基于对岩石裂纹的扩展和贯通机制的一系列相关研究基础[14-16],通过合理设置岩石的预置单裂纹的位置、方向(倾角)和尺寸,笔者采用基于扩展离散元(EDEM)的数值模拟研究手段,对在单轴压缩作用下的含单裂纹的岩石试样的裂纹起裂、扩展和贯通的演化规律进行研究,分析不同应力状态下试样的应力应变特征,以期研究结果能作为理论研究和试验研究的有益补充。
1 扩展离散元方法(EDEM)
离散单元法(distinct element method,DEM)是由P. A. CUNDALL[9]首次采用变形接触和显式、时间域的初始运动方程提出的特殊离散单元法程序,至今已有数十年的发展历史。通用离散元程序(universal distinct element code,UDEC)是一个处理不连续介质的二维离散元程序。UDEC用于模拟非连续介质承受静载或动载作用下的响应,如含节理、裂隙的岩体等。笔者采用的扩展离散元计算方法(expanded distinct element method,EDEM),是由长崎大学蒋宇静教授与中川教授基于UDEC计算程序框架进行二次开发,并由山东大学杨磊博士等人进一步完善,主要用以研究大规模岩石结构在拉-剪破坏时的裂纹扩展机制。关于基于UDEC计算程序的二次开发的具体介绍,以及笔者所采用的数值模拟方法在UDEC中的具体实现,可参考文献[10-11]和文献[17-18]相应介绍。
在EDEM计算程序中,岩体被认为是大量离散块体与块体间裂隙的集合体,其能较为真实地模拟岩体由于裂纹起裂、扩展、贯通而发生破坏过程中发生的一系列力学行为(包括压缩、滑移、分离等)和几何参数变化(包括方向、间距等)。数值模型中裂纹的发育过程主要通过4步来完成:①模型中潜在裂纹的定义;②块体接触面的应力计算;③接触面破裂与否的判断准则;④将潜在裂纹转化为真实裂纹。
从理论上来讲,裂纹在受外界压力作用时可能在模型中的任何位置、向任意方向扩展,所以潜在裂纹的合理性分布(位置及方向)是影响岩石破坏模拟结果准确性的关键因素。在EDEM模型中,嵌入六边形节理,其将无损岩体离散成大量六边形块体的集合体,如图1。

图1 EDEM模型的基本单元结构示意Fig.1 Schematic of basic unit structure diagram of EDEM model
块体间接触面表示潜在裂纹,具有较高的黏结强度,保证能在岩石破坏前表现出与真实岩体相似的力学性能。因此,当六边形块体的尺寸足够小时,新生裂纹就可以在任何区域内产生,并可沿任意方向扩展。六边形单元块体之间通过位于潜在裂纹处的“点接触”进行彼此联结,并向彼此施加作用力。为得到块体内部的应力、应变状态,将模型中每个单元块体划分并生成大量的三角形网格区。与此同时,潜在裂纹也被划分成若干段,它们均通过点接触相互联结。接触点主应力大小是通过选取形心至接触点距离最近的4个周边三角形网格区的平均应力进行估算得到,如图1。块体A中三角形网格区ZA1,ZA2和块体B中三角形网格区ZB1,ZB2这4个网格区域被用来计算位于潜在裂纹中心点处接触点的应力张量。
为评估EDEM模型中接触点是否达到临界破裂状态,文中模型计算分析过程中采用格里菲斯失效准则。在模型运算的每一步都将计算位于潜在裂纹上所有接触点的主应力,并将其替换到失效准则公式中去。当应力水平较低而岩石材料不发生破裂时,模型计算将自动进行下一步加载。随着应力逐渐增加,当某个接触点的应力状态满足失效准则时,与该接触点联结的潜在裂纹将转化成具有适当力学参数的真实裂纹,以此代表新生裂纹的起裂与扩展过程。通过以上程序,可以模拟不同边界条件下岩石材料的破坏过程。
2 数值模型
本次数值模拟所采用的模型长、高尺寸为W×HS=40 mm×100 mm,预置单裂纹长度为18 mm,如图2。模型底部竖向位移固定,轴向应力均匀施加在具有较高强度和刚度的加载板的上界面。考虑到数值计算中的计算量问题,在满足计算精度的要求下,最终确定模型中六边形单元块体的边长设置为1 mm,这样既能保证对裂纹扩展的合理模拟,又不会造成计算量过大的问题。单元块体间接触界面被预先定义为潜在裂纹,其代表了真实裂纹潜在的发育路径。岩体和裂纹的弹塑性变形行为分别采用摩尔-库伦准则和库伦滑移模型控制。

图2 数值模型示意Fig.2 Sketch of numerical model
参数设置方面,为了与笔者一系列的相关试验研究[14-16]具有对比性,数值模拟中的试件物理力学参数与试验保持一致:弹性模量E=28 700 MPa,泊松比ν=0.23,单轴抗压强度σc=47.4 MPa,抗拉强度σt=2.5 MPa。同时,经过大量的预备模拟试验,对所采用的数值模型参数体系不断进行调整、优化,使之与试验中表现出的力学现象相符合,最终确定各类裂纹的力学参数如表1。基于上述对数值模型的定义,充分论证裂纹分布的合理性,本次数值模拟方案共分5种情况,即考虑预置单裂纹的倾角α分别为15°,30°,45°,60°,75°的情况进行分析。

表1 模型参数
3 裂纹发展各阶段的定义和分析
预置单裂纹试样在轴向荷载作用下的损伤演化过程大体相似,均经历了前期应力集中、新生裂纹起裂、裂纹扩展及贯通破坏等阶段。本节以α=45°时的试样数值模拟全过程为例,从试样在加载不同阶段的应力分布变化、裂纹扩展过程及试样破坏模式等研究角度将裂纹的发展分为6个典型阶段。图3中,从左往右依次为裂纹起裂阶段、裂纹扩展Ⅰ~Ⅳ阶段和裂纹贯通阶段,对应的应力分为4.68,8.78,12.62,21.94,28.52,30.17 MPa)进行具体分析,以方便后文对含不同倾角预置裂纹试样在破坏过程中的差异性进行对比和进行相关规律性分析。
图3为α=45°时试样裂纹扩展不同阶段的拉、压应力分布。图3裂纹尖端深色区域以拉应力为主,其它区域以压应力为主,应力分布密度越大,说明该区域的应力集中程度越高。

图3 裂纹扩展不同应力阶段的拉、压应力分布(MPa)Fig.3 Stress distribution diagram of different stages of crack development
从图3中可知:①当应力达到4.68 MPa(约为峰值应力的15.5%)时,在预置裂纹的两尖端处开始产生新生裂纹,说明此时试样的单元块体接触面上所形成的应力值将要或已经达到破坏临界值,将此刻所受应力值记为试样的起裂应力。②随着荷载的增加,新生裂纹逐渐从预置裂纹尖端处起裂、扩展开来。从此刻裂纹扩展过程的方向变化可以看出,在裂纹扩展之初,其扩展方向基本与预置裂纹方向垂直,而随后逐渐变化成竖直方向,即与加载方向平行。③随着竖向荷载的进一步增加,新生裂纹最终沿着加载方向逐渐向试样的上下边界扩展。当应力达到30.17 MPa时,新生裂纹与试样上下边界贯通,试样发生整体损伤破坏,定义此时的应力为峰值应力。④在裂纹起裂阶段,拉应力主要集中于预置裂纹尖端区域,具体又可以分为两大区域,即与预置裂纹方向平行区域和与预置裂纹垂直区域。从图中可以看出,两大拉应力集中区均呈扇状分布,且在两者相重叠区域的拉应力集中程度最高,该位置正好紧紧围绕在预置裂纹的尖端处,意味着当应力集中程度达到试样单元块体接触面的破坏临界值时,新生裂纹将首先在预置裂纹尖端产生。之后,随着新生裂纹的不断扩展,拉应力分布范围和应力集中区域逐渐随着新生裂纹的尖端位置的变化而变化。在裂纹扩展后期,拉应力在裂纹尖端区域的集中程度减弱,说明裂纹正处于后期不稳定扩展阶段,该阶段的新生裂纹的扩展不再需要显著的应力集中来驱使。⑤注意到在试样加载全程,预置裂纹尖端区域始终存在一定范围的拉应力分布区,说明预置裂纹(或者说原始缺陷)对岩石内部的应力分布及破坏形态始终存在一定程度的影响。
4 数值模拟结果对比分析
含不同倾角的预置裂纹试样在加载全程的裂纹扩展及损伤演化机制等方面存在一定共性,但与此同时也存在着诸多方面的差异性。总体而言,新生裂纹的起裂位置均位于预置裂纹的尖端部位,并在扩展前期阶段裂纹扩展方向基本与预置裂纹方向垂直,此后裂纹扩展方向基本与加载方向平行。值得注意的是,预置裂纹倾角为60°和75°试样时,在加载中后期,沿预置裂纹周边出现若干新生裂纹,可能是试样出现劈裂破坏,但其对试样最终破坏形态影响不大。在数值模拟中,提取了裂纹发展6个典型阶段的应力值作对比分析。图4给出了预置裂纹倾角α分别 15°,30°,45°,60°,75°时的试样在不同加载阶段所对应的应力值。
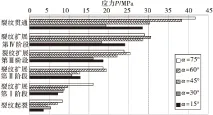
图4 裂纹发展各阶段应力值比较Fig.4 Stress comparison chart of different stages of crack development
从图4中可知:①随着施加的应力值的增大,试样经历了新裂纹的起裂、扩展和贯通等阶段。②随着预置裂纹倾角α的增加,各不同阶段均在总体上表现出应力值不断增大的趋势,但也会出现个别奇异点。下文将具体针对不同试样间的“起裂应力”、“裂纹扩展速率”、“试样破坏模式”及“试样的抗压强度”等方面进行的相应结果进行具体的对比和分析。
4.1 不同试样的“起裂应力”对比分析
图5为数值模拟结果在试样起裂应力方面的对比统计,即图4中不同α下的裂纹起裂应力对比。从图5中可以看出:①随着预置裂纹倾角α的增加,起裂应力总体呈上升趋势。当预置裂纹倾角α=15°,30°时,新裂纹的起裂应力较小。当α=60°,75°时,起裂应力有相对较大的提高。结合相关试验分析可知[15],前者新裂纹的扩展主要受张拉应力控制,后者主要受剪切应力控制,受剪切应力控制的裂纹更不易扩展。②当倾角α=45°时,裂纹的起裂应力产生突降,推测此时裂纹起裂模式可能发生转变,α=45°是新裂纹扩展模式转变的临界角,至于具体转变模式详见后文分析。

图5 起裂应力对比Fig.5 Crack initiation stress comparison diagram
4.2 不同试样间“裂纹扩展速度”对比分析
为了解新生裂纹在加载全程的不同阶段的发育、扩展速率,图6给出了不同试样对应不同加载阶段的裂纹扩展长度量化曲线(图中a为初始裂纹长度)。即测量出试样加载不同阶段的新生裂纹扩展长度,然后将此长度与预置裂纹初始长度的比值作为裂纹扩展的量化长度,绘出此量化长度随试样加载应力的变化曲线,以此分析新裂纹的扩展速度。
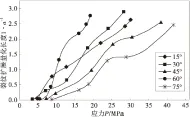
图6 不同加载阶段的裂纹扩展长度量化曲线Fig.6 Length quantization curve of crack growth under different loading levels
从图6可知:①在裂纹起裂扩展的前期,预置裂纹倾角α=30°,45°时试样的裂纹扩展速率相对其他试样较大,说明此倾角下的新生裂纹起裂后能够在较小的应力增量作用下完成裂纹的持续扩展;而α=15°,60°,75°时试样在裂纹起裂后则需要施加相对较大的应力才足以促使裂纹继续发育,即α=30°,45°时有利于新裂纹的初期扩展。②在裂纹扩展中期;除α=45°的试样外,其他试样裂纹扩展速率均有所提升;α=45°时试样裂纹扩展速率反而降低成匀速扩展状态,与其他试样相比其裂纹扩展速率变为最低。③在裂纹扩展后期,各试样的裂纹发育速率基本都有所减缓,直至最后贯通。④从裂纹平均扩展速率来看,预置裂纹倾角α=30°时的试样裂纹扩展最为迅速;α=15°,45°,60°,75°时的试样扩展速率依次减弱。从整体曲线发展趋势来看,除α=75°时的试样在应力为25~30 MPa间出现平缓发展阶段,其他试样的裂纹扩展长度量化曲线无显著转折阶段,较难类比区分出稳定扩展阶段与非稳定扩展阶段。
4.3 不同试样“破坏模式”对比分析
图7为数值模拟得出的试样断裂破坏形态,图中线条表示新裂纹的扩展、贯通路径。

图7 试样破坏模式示意Fig.7 Failure patterns of specimens
由图7可知:①试样新生裂纹均从预置裂纹的尖端开始发育,并逐渐沿加载方向扩展至试样的上下边界,且在扩展路径上具有很高的相似性。其差异主要体现在裂纹起裂模式不同,当α=15°,30°时,新裂纹从预置裂纹尖端的两翼开始扩展;当α=60°,75°时,新裂纹的扩展逐渐向着预置裂纹两侧纵深发展;当α=45°时,新裂纹的起裂处于上述两种模式的过渡阶段。②预置裂纹倾角α分别与45°,60°,75°试样裂纹扩展模式上有所不同。由于数值模拟中将格里菲斯拉裂准则定义为模型破坏准则,故数值模拟结果中主要是张拉破坏,基本没有次生裂纹产生。预置裂纹倾角α为60°,75°时,试样预置裂纹周边的短小的新生裂纹基本属于劈裂张拉裂纹。结合相关试验研究可知[15],数值模拟中对模型破坏准则的定义具有局限性,格里菲斯拉裂准则预先假定了裂纹的起裂是由张拉应力控制的,无法反映实际情况中试样存在剪切破坏的情况。
4.4 不同试样“抗压强度”对比分析
图8为数值模拟中不同试样的抗压强度对比曲线,即图4中不同α下裂纹贯通时的应力对比。

图8 试样抗压强度对比Fig.8 Peak strength comparison diagram
从图8中可知:①随着预置裂纹倾角α的增加,试样的抗压强度总体呈上升趋势,表现出和不同试样的起裂应力一致的规律,说明试样的单轴抗压强度和裂纹的起裂应力是一致的。②和图5相似的是,当α=30°时出现奇异点,所不同的是α=30°的试样的起裂应力比α=15°,45°时的偏大,而抗压应力却偏小,说明当α=30°时,新生裂纹较难起裂但却较易贯通。分析其原因,从图5中可知,α=30°时试样的起裂应力较大,说明此时试样新裂纹的起裂需要积蓄较高的能量,但从图6中可知,α=30°时试样裂纹的平均扩展速率最大,远快于α=15°,45°时的情况,说明新裂纹起裂后能量释放得较多,因此,在裂纹最后贯通时所剩余的能量反而较小,从而降低了试样的单轴抗压强度。
5 结 论
通过数值模拟方法研究了含不同倾角的预置单裂纹的岩石试件在单轴压缩下的裂纹起裂、扩展和破坏的演化规律。得出结论如下:
1)随着预置裂纹倾角α的增大,新裂纹的起裂应力和试样的抗压强度总体上呈增大趋势,但当α=30°时会出现突变,与α=15°,45°时的情况相比,α=30°时试样的新生裂纹较难起裂,但起裂后试样裂纹扩展最为迅速,试样的抗压强度也最低。
2)α=30°,45°时有利于新裂纹的初期扩展;在裂纹扩展中期,α=45°时试样裂纹扩展速率开始降低为匀速状态,且与其他试样相比其裂纹扩展速率变为最低;在裂纹扩展后期,各试样的裂纹扩展速度开始变缓,直至最后贯通。从裂纹扩展平均速率来看,α=30°时的试样裂纹扩展速率最大,α=15°,45°,60°,75°时的试样扩展速度依次减弱。
3)当α=15°,30°时,新裂纹从预置裂纹尖端的两翼开始扩展;当α从45°增大到75°时,新裂纹的扩展逐渐向着预置裂纹两侧纵深发展,α=45°时为两种不同裂纹扩展模式的过渡倾角。
[1] BELYTSCHKO T, BLACK T. Elastic crack growth in finite elements with minimal remeshing[J].InternationalJournalforNumericalMethodsinEngineering, 1999, 45(5): 601-620.
[2] SUKUMAR N, PREVOST J H. Modeling quasi-static crack growth with the extended finite element method. part I: computer implementation[J].InternationalJournalofSolidsandStructures,2003, 40(26): 7513-7537.
[3] PATHAK H, SINGH A, SINGH I V. Fatigue crack growth simulations of 3-D problems using XFEM[J].InternationalJournalofMechanicalSciences, 2013, 76(11): 112-131.
[4] BROUMAND P, KHOEI A R. The extended finite element method for large deformation ductile fracture problems with a non-local damage-plasticity model[J].EngineeringFractureMechanics, 2013, 112(11): 97-125.
[5] ZHANG Y L, FENG X T. Extended finite element simulation of crack propagation in fractured rock masses[J].MaterialsResearchInnovations, 2011, 15(Sup1): 594-596.
[6] BELYTSCHKO T, GU L, LU Y Y. Fracture and crack growth by element free Galerkin methods[J].ModellingandSimulationinMaterialsScienceandEngineering, 1994, 2(3A): 519-534.
[7] KRYSL P, BELYTSCHKO T. The element free Galerkin method for dynamic propagation of arbitrary 3-D cracks[J].InternationalJournalforNumericalMethodsinEngineering, 1999, 44(6): 767-800.
[8] RAO B N, RAHMAN S. Probabilistic fracture mechanics by Galerkin meshless methods-part I: rates of stress intensity factors[J].ComputationalMechanics, 2002, 28(5): 351-364.
[9] CUNDALL P A. A computer model for simulating progressive large scale movements in block system[C]//ProceedingoftheSymposiumoftheInternationalSocietyforRockMechanics. Nancy, France:[s.n.], 1971.
[10] YANG L, JIANG Y J, LI S C. Experimental and numerical research on 3D crack growth in rocklike material subjected to uniaxial tension[J].JournalofGeotechnicalandGeoenvironmentalEngineering, 2013, 139(10): 1781-1788.
[11] JIANG Y J, LI B, YAMASHITA Y J. Simulation of cracking near a large underground cavern in a discontinuous rock mass using the expended distinct element method[J].InternationalJournalofRockMechanics&MiningSciences, 2009, 46(1): 97-106.
[12] 蒋明镜, 陈贺, 刘芳. 岩石微观胶结模型及离散元数值仿真方法初探[J]. 岩石力学与工程学报, 2013, 32(1): 16-23. JIANG Mingjing, CHEN He, LIU Fang. A microscopic bond model for rock and preliminary study of numerical simulation method by distinct element method[J].ChineseJournalofRockMechanicsandEngineering, 2013, 32(1): 15-23.
[13] 周喻, 吴顺川, 许学良, 等. 岩石破裂过程中声发射特性的颗粒流分析[J]. 岩石力学与工程学报, 2013, 32(5): 951-959. ZHOU Yu, WU Shunchuan, XU Xueliang, et al. Particle flow analysis of acoustic emission characteristics during rock failure process[J].ChineseJournalofRockMechanicsandEngineering, 2013, 32(5): 951-959.
[14] ZHAO C, MATSUDA H, MORITA C, et al. Study on failure characteristic of rock-like materials with an open-hole under uniaxial compression[J].Strain, 2011, 47(5): 405-413.
[15] 赵程, 田加深, 松田浩, 等. 单轴压缩下基于全局应变场分析的岩石裂纹扩展及其损伤演化特性研究[J]. 岩石力学与工程学报, 2015, 34(4): 763-769. ZHAO Cheng, TIAN Jiashen, MATSUDA Hiroshi, et al. Study on the crack propagation and damage evolution characteristics of rock based on the global strain field under uniaxial compression[J].ChineseJournalofRockMechanicsandEngineering, 2015, 34(4): 763-769.
[16] 赵程, 鲍冲, 松田浩, 等. 数字图像技术在节理岩体裂纹扩展试验中的应用研究[J].岩土工程学报,2015,37(5): 944-951. ZHAO Cheng, BAO Chong, MATSUDA Hiroshi, et al. Application of digital image correlation method in experimental research on crack propagation of brittle rock[J].ChineseJournalofGeotechnicalEngineering, 2015, 37(5): 944-951.
[17] YANG L, JIANG Y J, LI B, et al. Estimation of dynamic behaviors of bedrock foundation subjected to seismic loads based on FEM and DEM simulations[J].KSCEJournalofCivilEngineering, 2013, 17(2): 342-350.
[18] YANG L, JIANG Y J, LI S C, et al. Experimental and numerical research on 3D crack growth in rocklike material subjected to uniaxial tension[J].JournalofGeotechnicalandGeoenvironmentalEngineering, 2013, 139(10): 1781-1788.
Numerical Simulation of Single Crack Propagation and Damage Evolution Mechanism of Rock Specimens
ZHAO Cheng1,2, LIU Fengming1,2, YANG Lei3, TIAN Jiashen1
(1. Department of Geotechnical Engineering, Tongji University, Shanghai 200092,P.R.China; 2. Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education, Tongji University, Shanghai 200092, P.R.China; 3. School of Civil and Hydraulic Engineering, Shandong University, Ji’nan 250061, Shandong, P.R.China)
The whole process of crack initiating, propagation and through of rock specimen with single crack at various preset inclination angles under single axial compression was simulated by use of extended distinct element method (EDEM) and the stress variation in crack spreading stages was investigated and explored and the mechanism of single crack spreading with various preset inclination angles was analyzed. The results show that with the increase of inclined angle α of preset crack, the crack—starting stress of new cracks and compressive strength of the specimen are in overall tendency of increasing and sharp change occurred when α=30°. The crack developed most rapidly when α=30° . When α=15°, 45°, 60°, 75°, the crack expanding speed reduced progressively in order. When α=15° and α=30° , the new crack started expanding from the two wings of tip end of the pre-existing crack. When α increased from 45° to 75° , the new crack expanded gradually toward vertical depth along bilateral sides of the pre-existing crack. α=45° is the inclined angle at the transition of the two different crack expanding patterns.
tunnel engineering; geotechnical engineering;extend distinct element method (EDEM); numerical simulation; rock material; single crack
10.3969/j.issn.1674-0696.2016.05.06
2015-07-01;
2016-01-12
国家自然科学基金项目(41202193;41572262)
赵 程(1982—),男,内蒙古呼和浩特人,副教授,博士,主要从事岩土工程方面的研究。E-mail:zhaocheng@tongji.edu.cn。
U452.1+2;TU458
A
1674-0696(2016)05-022-06
