重载作用对混凝土路面板的弯沉及应力分析

辛 勤，孙吉书，任晓军，张小冉

(1. 河北工业大学 土木工程学院，天津 300401；2.天津铁道职业技术学校，天津 300240)

重载作用对混凝土路面板的弯沉及应力分析

辛 勤1，孙吉书1，任晓军2，张小冉1

(1. 河北工业大学 土木工程学院，天津 300401；2.天津铁道职业技术学校，天津 300240)

运用ANSYS有限元软件建立路面结构三维实体模型，用正弦荷载模拟车辆随机荷载运动，分别就路面结构竖向位移及应力变化进行重载作用模拟分析；并分析超载率与脱空尺寸的影响。研究表明：动荷载作用下面板产生的弯沉值及板底最大拉应力值随着水泥混凝土路面板板底脱空区的面积增大而增大；超载率越大且脱空面积越大，板的竖向位移和拉应力增幅越大。

道路工程；动荷载；力学响应；有限元分析

目前交通运输呈现重载化趋势[1-2]，实际情况中路面承受的荷载远大于我国高等级路面规定的车辆极限轴载(10 t)[3-4]。重型车辆荷载的频繁通过导致路面板角和接缝处产生更大挠度[5]，进而增大脱空面积并加速面板破坏，如此周而复始，形成恶性循环[6]。因此有必要了解路面结构受力特性，针对性地对重载现象造成影响提出预警，这对于预防和维修意义重大。鉴于此，笔者建立有限元三维实体模型，重点分析在重载作用下，车辆荷载对有脱空路面板的力学影响，并讨论脱空尺寸及超载率的影响。

1 水泥混凝土路面计算模型

1.1 计算参数

采用大型有限元分析软件ANSYS，选择4层弹性层状体系进行路面结构计算。计算单元选取SOLID45单元和SURF154单元，计算参数见表1。采用映射网格划分模式，对板底脱空区及荷载作用区域进行网格加密提高计算精度[7]。水泥混凝土路面的计算模型与网格划分如图1。

表1 模型计算参数

图1 路面计算模型Fig.1 Calculation model of the pavement

1.2 车辆荷载简化

采用近似正弦的简谐振动模型对车辆随机荷载进行简化[8]。其表达式为

p(t)=p0+psin(ωt)

(1)

式中：p0为车辆静载，取车辆单边轮载p0=50 kN；p为振动荷载幅值，p=M0uw/r(y)ω2〔M0为车辆模型簧下质量，M0=1 200 N·s2/m，ω为振动圆频率，uw/r(y)为路面不平度函数，uw/r(y)=2 mm(国际不平度标准指标)〕。

2 重载作用下面板应力与弯沉分析

为了模拟车辆的运动荷载作用，在模型上施加荷载类型为阶跃载荷。轮载加载于一组单元上的持续时间设置为0.004 5 s，然后轮载向前移动一个单元再持续0.004 5 s，即在每个单元上的加载均持续0.009 s，相当于车速为22.22 m/s(80 km/h)。当只要改变载荷的持续时间，就可以建立不同的车速下的路面模型，从而对不同工况进行分析。为节约篇幅，笔者只列举80 km/h工况分析，在本节最后给出各车速影响线。

2.1 弯沉分析

选取车辆荷载模型BZZ-100，以80 km/h速度行驶，板角脱空面积为0.4 m×0.4 m。绘制3个时间点作用下的面板弯沉云图〔图2(a)～图2(c) 〕，以脱空区板面中心节点为观测点绘制弯沉时程曲线，如图2(d)。

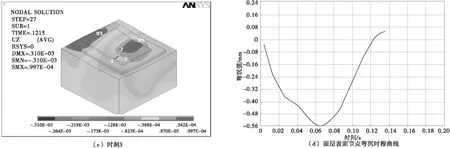
图2 弯沉云图和弯沉时程曲线Fig.2 Deflection nephogram and deflection time-history curve

通过图2可以看到，深色区域代表汽车轮胎荷载区域，也是弯沉值最大区域。随着荷载的移动及作用时间的增长，弯沉值最大区域逐渐扩大，基层垫层地基等变形也在逐渐增大。荷载作用于脱空的板面时，面板的弯沉值增长较大，远离脱空区后，弯沉值变化较小。由时程曲线可以看出，荷载作用弯沉值最大时刻为0.067 5 s，此时最大弯沉值为0.658 mm，为车辆荷载经过板角脱空区域的时刻，且最大弯沉发生在板角脱空区。

2.2 应力分析

以脱空区中点以下对应的各结构层节点为观察点，绘制最大应力时程曲线如图3。当荷载作用在脱空区中点时，面板表层和底层节点产生最大拉应力或压应力；基层处也受到一定拉应力作用；随着车辆荷载逐渐驶离脱空区，各节点应力恢复至中轴附近。t=0.022 s时板底处产生最大拉应力0.656 MPa。

图3 路面结构各节点的应力时程曲线Fig.3 Stress-time curves of various nodes of the pavement structure

各车速对板面弯沉值和板底拉应力影响如图4。由图4可知，板底拉应力以及板面的竖向位移随车辆运动速度的增加而减小，但随着车速的增加影响逐渐变小。

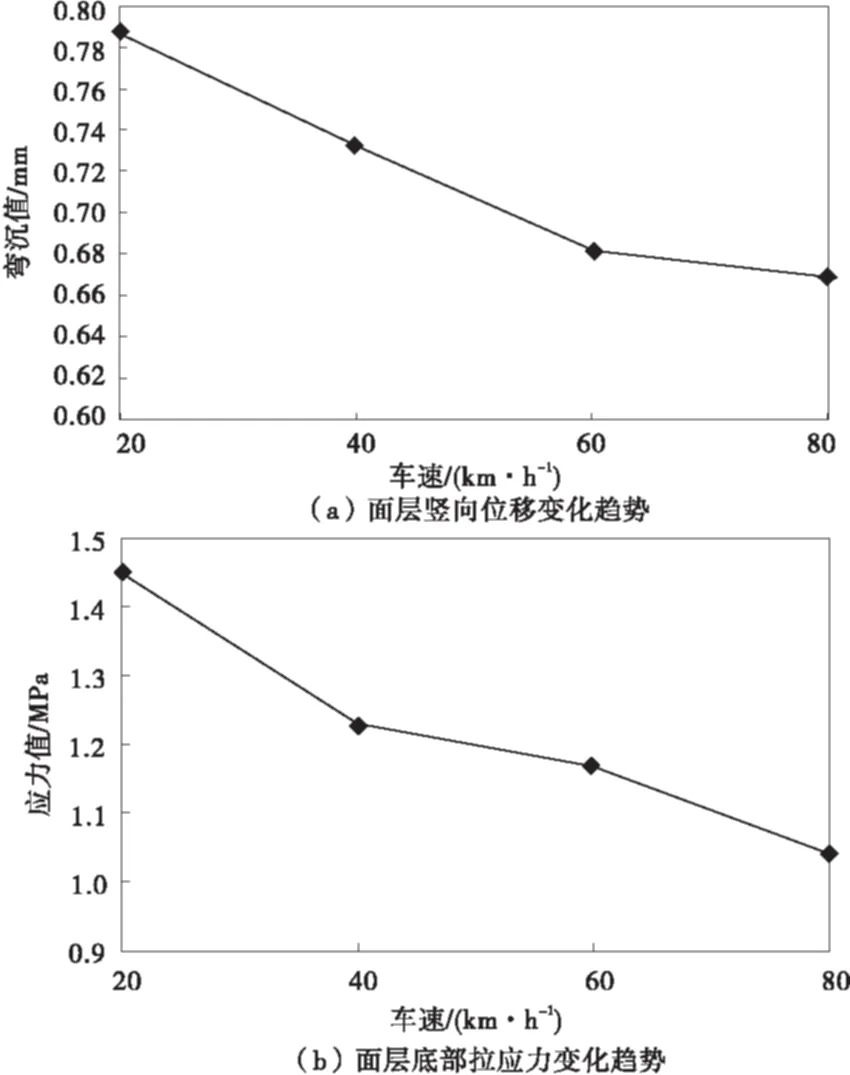
图4 不同车速下竖向位移和拉应力的变化趋势Fig.4 Change trend of the vertical displacement and the tensile stress with different speed of vehicle

3 脱空尺寸的影响

对不同脱空尺寸的水泥混凝土面板进行有限元模拟加载计算，计算结果汇总见表2。由表2可以看出，随着脱空面积的增大，水泥混凝土路面的最大竖向位移值和板底拉应力值都在逐渐增大。当尺寸为40 cm时所产生的最大应力值比无脱空时增大了68.9%，面层最大位移比无脱空时增大了79.8%；当脱空面积由40 cm增大到120 cm时，最大应力值增大了34.3%，竖向位移值增大了39.2%。这说明水泥混凝土面板在脱空刚开始形成时，板底最大应力以及竖向位移会发生较大的改变，随着脱空尺寸的增大，受力与变形也会随之增大，但是增加的幅度将会逐渐变小。

表2 重载作用下不同脱空尺寸的面板弯沉与应力

4 超载率的影响

设置试验车辆的中心轮距为34 cm，轴距设为180 cm，以标准轴载100 kN为额定轴载，采用经验关系式[9]计算出不同超载率下荷载。荷载工况计算结果见表3。

p=0.004 2P+0.29pi+0.144 8

(2)

式中：p为轮胎接地压力；P为双轮轮胎荷重；pi为轮胎充气压力。

表3 超载分析荷载工况

在水泥混凝土路面结构模型上，设置从40～160 cm不同尺寸大小的脱空区，在模型上施加4种工况，计算后得到弯沉值和应力值见表4。

表4 不同超载率轴载作用下的路面结构弯沉值和最大应力

为更直观地观察到不同脱空面积和超载率的耦合作用对结构弯沉及应力值的影响，采用折线图将变化趋势表示出来,见图5。

图5 不同超载率对路面板竖向位移和板底拉应力的影响曲线Fig.5 The effect curve of different overload rate on the vertical displacement of pavement and the tensile stress of slab bottom

当脱空面积为40 cm×40 cm，车辆轴载的超载率从0%增加到100%时，路面弯沉值增加了62.5%，板底产生的最大拉应力值增长了40.2%；当脱空面积为160 cm×160 cm，车辆轴载的超载率从0%增加到100%时，路面的竖向位移增加了128.3%，最大拉应力增长了109.5%。由此可知，脱空面积越大，超载率越大，对于面板的损坏就越大。

5 结 论

1)用简谐正弦荷载模拟重型车辆随机荷载作用，作用在三维实体模型上，得到最大弯沉发生在板角脱空区附近。脱空尺寸40 cm×40 cm，额定轴载以80 km/h作用下产生最大弯沉值为0.658 mm；脱空中点可产生的最大拉应力为1.02 MPa；随着速度的增大影响减小。

2)超载率一定时，随着脱空尺寸增大，弯沉值及拉应力值均在增大；脱空尺寸一定时，随着超载率的增大，弯沉值及应力值均增大；并且脱空尺寸越大，超载率越大，弯沉值与应力值增长幅度越大，对面板的损坏也就越大。

3)重载作用破坏机制：混凝土路面板受到重型荷载的反复作用，面板的板边及板角受到应力最大，变形也最大，导致出现不可恢复塑性变形，从而导致脱空区的出现。脱空区一旦出现，荷载对面板的破坏就越大，形成恶性循环，直至路面板发生破坏。

[1] 王选仓,于伟,冯治安,等.重载水泥混凝土路面极限轴载计算方法[J].中国公路学报,2013,26(5):21-27. WANG Xuancang, YU Wei, FENG Zhi’an, et al. Calculation methods for ultimate axle load on cement concrete pavement under heavy load[J].ChinaJournalofHighwayandTransport,2013,26(5):21-27.

[2] 张艳聪,赵队家,刘少文,等.考虑层间接触时基层参数对水泥路面力学特性的影响[J].重庆交通大学学报(自然科学版),2014,33(2):49-52. ZHANG Yancong, ZHAO Duijia, LIU Shaowen, et al. Impacts of base parameters on mechanical properties of cement pavement considering interlayer contact[J].JournalofChongqingJiaotongUniversity(NaturalScience),2014,33(2):49-52.

[3] 林仕雄.水泥混凝土路面损坏原因分析及处理方案比选[J].公路,2006(8):201-205. LIN Shixiong. Cement concrete pavement damage causes and treatment alternatives[J].Highway,2006(8):201-205.

[4] 赵艳玲.重载对水泥混凝土路面损坏机理与对策研究[D].哈尔滨:哈尔滨工业大学,2006. ZHAO Yanling.StudyonMechanismofCementConcretePavementDamageofHeavy-DutyTrafficRoadandCountermeasures[D]. Harbin: Harbin Institute of Technology,2006.

[5] 杨春风,解帅,孙吉书. 基于路面不平整度的车辆动荷载系数分析[J].重庆交通大学学报(自然科学版),2015,34(4):77-81. YANG Chunfeng, XIE Shuai, SUN Jishu. Vehicle dynamic load coefficient analysis based on pavement roughness[J].JournalofChongqingJiaotongUniversity(NaturalScience),2015,34(4):77-81.

[6] JEONG Jin-Hoon, PARK Joo-Young, LIM Jin-Sun, et al. Testing and modelling of friction characteristics between concrete slab and subbase layers[J].RoadMaterialsandPavementDesign,2014,15(1):114-130.

[7] 古芸琳,何相呈,杨倩荣. 路基干湿状态对沥青路面力学响应的影响[J].重庆交通大学学报(自然科学版),2013,32(1):32-36. GU Yunlin, HE Xiangcheng, YANG Qianrong. Influence of subgrade dry-wet state on mechanical response of asphalt pavement[J].JournalofChongqingJiaotongUniversity(NaturalScience),2013,32(1):32-36.

[8] 曹源文,梁乃兴,于清,等.路面不平整引起的车辆动载计算方法[J].交通运输工程学报,2008,8(2):69-73. CAO Yuanwen, LIANG Naixing, YU Qing, et al. Calculating method of vehicle dynamic load caused by uneven pavement[J].JournalofTrafficandTransportationEngineering,2008,8(2):69-73.

[9] 王秉纲,郑木莲.水泥混凝土路面设计与施工[M].北京:人民交通出版社,2004. WANG Binggang, ZHENG Mulian.DesignandConstructionofCementConcretePavement[M]. Beijing: China Communications Press,2004.

Overloading Effect on Concrete Pavement Deflection and Stress Analysis

XIN Qin1, SUN Jishu1, REN Xiaojun2, ZHANG Xiaoran1

(1. School of Civil Engineering, Hebei University of Technology, Tianjin 300401, P. R. China; 2. Tianjin Railway Technical and Vocational College, Tianjin 300240, P. R. China)

ANSYS software was used to establish 3D entity model of the pavement structure, and sine load was used to simulate the random load movement of the vehicle. The vertical displacement and stress change of the pavement structure under overloading were simulated and analyzed respectively. And then the effect of overloading rate and cavity size were also analyzed. The conclusion shows that: in the case of dynamic load, the panel deflection value and the bottom maximum tensile stress increase with the increment of the cavity size of the bottom plate board of concrete pavement; moreover, with the higher of overload rate and the larger of void area, the increase of the vertical deflection and tensile stress is greater.

highway engineering; dynamic load; mechanical response; finite element analysis

2015-06-25；

2015-09-25

河北省高等学校科学研究青年基金项目(Q2012156)

辛 勤(1987—)，女，河北保定人，博士研究生，主要从事道路及结构工程方面的研究。E-mail：xinxin19870521@126.com。

10.3969/j.issn.1674-0696.2016.06.07

U426.216

A

1674-0696(2016)06-030-04