缆索承重桥近距离并列索气动力的雷诺数效应

杜晓庆，张利平，刘庆宽

(1. 上海大学 土木工程系，上海 200072；2. 石家庄铁道大学 风工程研究中心，河北 石家庄 050043；3.河北省大型结构健康诊断与控制重点实验室，河北 石家庄 050043)

缆索承重桥近距离并列索气动力的雷诺数效应

杜晓庆1，张利平1，刘庆宽2,3

(1. 上海大学 土木工程系，上海 200072；2. 石家庄铁道大学 风工程研究中心，河北 石家庄 050043；3.河北省大型结构健康诊断与控制重点实验室，河北 石家庄 050043)

近距离并列索在工程实际中有着广泛的应用，但针对并列索的气动性能及其雷诺数效应的研究并不多，特别是在临界雷诺数区域。通过风洞试验，在雷诺数Re=0.9×105～3.2×105之间(涉及亚临界雷诺数和临界雷诺数)研究了近距离双圆柱的气动性能及其雷诺数效应。研究结果表明：近距离双圆柱的气动性能有强烈的雷诺数效应，在不同的风攻向角下，临界雷诺数的圆柱平均气动力系数与亚临界区有很大差异；在临界雷诺数区域，下游圆柱的平均升力系数可达到1.35以上，平均升力系数与阻力系数会随雷诺数的变化发生不连续突变，这应该是流态发生了变化；上游圆柱的平均升力系数可达1.0以上，平均升力系数会随雷诺数的变化发生不连续突变，这种气动力的突变与双圆柱绕流场的流态结构的变化有关。

桥梁工程；缆索承重桥；风洞试验；圆柱绕流；雷诺数效应

0 引 言

伴随着经济社会的飞速发展，对交通工程构造物提出了愈来愈高的要求，各种大跨径桥梁应运而生。在众多的桥梁体系中，缆索承重桥因其受力性能优越、节省材料和外形美观等诸多优点，成为了大跨度桥梁的最主要桥型。其中，近距离并列索在工程实际中得到了广泛的应用，如连接丹麦和瑞典的厄勒海峡大桥的并列斜拉索间距为2.68D。

前人对于错列双圆柱已经开展了大量研究，结果表明错列双圆柱周围流场存在着相当的复杂性，并且流场会随着两柱圆心间距P与风攻向角α的变化而变化。流场的复杂性主要体现在分离的自由剪切层相互干扰、卡门涡脱的形成与消失、卡门涡街的相互作用等。对于这种复杂流场的划分，前人也有多种不同的划分方法，如M.M.ZDRAVKOVICH[1]根据双柱位置将双柱流场划分为两种：①尾流干扰区。此时双柱中某一柱部分或完全处于另一柱的尾流中；②邻近干扰区。此时双柱互相靠近，均不处在对方的尾流中。顾志福等[2]将这种划分扩展为3种，即尾流干扰、剪切层干扰和邻近干扰，分别出现在α=0～9.65°，9.7～15°和16～90°。D.SUMNER等[3]通过流态可视化与粒子成像技术(PIV)，观测了双柱在P/D=1.0～5.0，Re=850～1 900时的流态变化，并根据P-α变化将流场划分为3种：①单柱态。P/D=1.0～1.125，α=0～90°，此时双柱等效于单柱，并且只有单一的涡脱频率；②小风攻向角态。P>1.125，α=0～20°，此时将会发生剪切层再附或是涡脱撞击在下游柱表面；③大风攻向角态。P>1.125，α=20～90°，此时会出现旋涡的摞合、分离、同步等现象。

S.J. PRICE等[4]，M.M.ZDRAVKOVICH等[5]探究了错列双圆柱的时均气动力，但是主要偏重于下游柱；M.M.ALAM等[6]则对错列双圆柱的时均气动力作了系统性研究。Y.ZHOU等[7]研究了P/D= 1.2～4.0，α=0～90°，Re=1.5×103～2.0×104时St的雷诺数效应，发现St与Re之间存在着定性的关系，并把St-Re的关系划分为4大类。D.SUMNER[8]对错列双圆柱做了综述性工作。

以上所述错列双圆柱的研究中，其雷诺数要么是给定的，要么只是很小的一段范围。但是，对于错列双圆柱的雷诺数效应研究非常少，尤其是在高雷诺数下(Re>1×105)。本研究的目的在于探明错列双圆柱的气动力系数在临界区的雷诺数效应，并结合流态分类对试验结果进行分析。其中P/D=2，α=0～90°，Re=8.9×104～3.2×105。

1 风洞试验

1.1 试验模型和试验工况

试验采用两根直径相同的刚性圆柱节段模型，圆柱模型由有机玻璃圆管制成，表面光滑。圆柱固定安装在试验支架上。图1为两根圆柱模型的相对位置和来流的关系。图中，圆柱A为测力圆柱，圆柱B为干扰圆柱，L为顺风向圆心间距、T为横风向圆心间距、D为圆柱直径，两圆柱的圆心间距可调。圆柱模型的直径均为0.14 m，圆柱的两个端部均安装了导流板，以模拟二维流场。圆柱A长1.4 m(10D)，圆柱B长1.68 m(12D)。

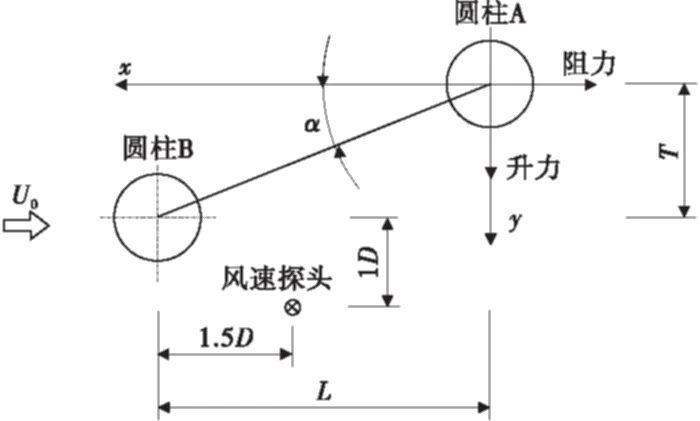
图1 圆柱的相对位置和气动力方向定义Fig.1 Relative position of circular cylinder and the definition of aerodynamics directions

试验雷诺数在0.9×105～3.2×105之间，涉及亚临界区和临界区。顺风向圆柱间距L的试验范围为2D～12D，横风向间距T的试验范围为0～3D。试验过程中圆柱A的位置固定，干扰圆柱B的位置可变，总共进行了110个圆柱相对位置的试验，试验工况总数860余个。限于篇幅，笔者仅给出了双柱圆心间距为P/D=2的研究结果，两圆柱的相对位置见图2。

图2 圆柱B的位置布置Fig.2 Location of the cylinder B

1.2 试验风洞和测试设备

本试验是在石家庄铁道大学风工程研究中心的风洞实验室完成。该风洞为串联双试验段回/直流边界层风洞，其中，低速试验段转盘中心处长为24.0 m，宽为4.38 m，高为3.0 m，最大风速在30.0 m/s以上；高速试验段长为5.0 m，宽为2.2m，高为2.0 m，最大风速可达80.0 m/s以上。本试验在高速试验段进行。

圆柱A端部安装了高频测力天平，测试其受到的气动力时程。测力使用美国ATI公司生产的Delta系列六分量高频测力天平，两个量程分别为165和330 N，测量频率为1 500 Hz。试验还测量了圆柱B的尾流风速，风速测试使用的是Series 100眼镜蛇探头，最大风速量程对应压力3 000 Pa，测量频率为2 000 Hz，风速测试的探头位置见图1。气动力和风速的采样时间均为30 s。

1.3 气动力定义

圆柱的气动力方向如图1。阻力以顺风向为正(x轴负方向为正)；升力以向下为正(y轴正方向为正)。顺风向平均阻力系数CD和横风向平均升力系数CL的定义如下：

(1)

(2)

式中：ρ为空气密度；D为圆柱直径；U0为来流风速；Fx和Fy为作用在单位长圆柱模型上的阻力和升力。

2 试验结果与分析

对于双圆柱的气动性能和绕流场流态结构，雷诺数、圆柱间距和风攻角是最重要的3个控制参数。在本研究中，采用圆柱的顺风向间距(L)和横风向间距(T)来反映圆柱间距和风攻角这两个参数，如表1。

表1 工况参数

下文对小间距(P/D=2)双圆柱的试验研究结果进行分析和讨论。

2.1 下游柱

错列双圆柱下游柱气动力系数随雷诺数变化结果见图3。

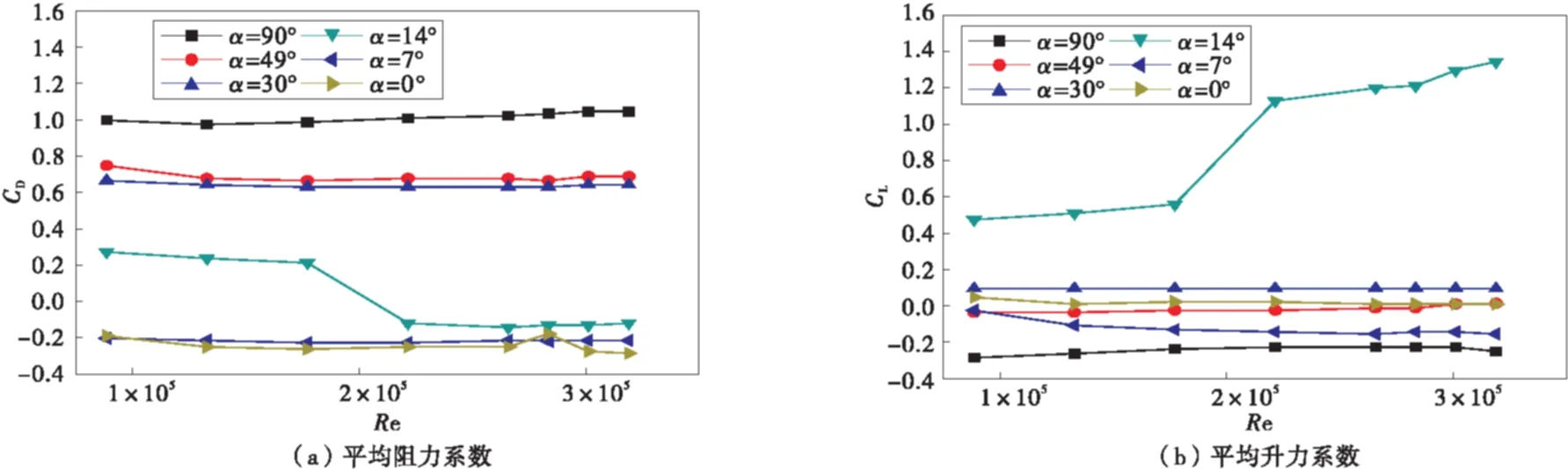
图3 错列双圆柱下游柱气动力系数随雷诺数变化Fig.3 Downstream aerodynamic coefficients of staggered double circular cylinders changing with Reynolds number

从图3(a)可以看出，在α=0°时，此时双圆柱处于串列布置，平均阻力系数CD<0，即下游柱受到方向指向上游圆柱的吸力，约为-0.2，小于单柱时的气动阻力系数，并且不随着Re的变化而变化。α=7°时，CD≈-0.2，与α=0°时类似。

当α=14°时，可以看到气动阻力系数变化剧烈，雷诺数效应颇为明显。在Re=1.77×105～2.2×105时，气动阻力系数急剧减小，由0.21减至-0.12，即双柱之间由原来的斥力转变为吸力，在Re=2.2×105～3.19×105之间时又趋于稳定，约为-0.1。当α≥30°时，气动阻力系数随着雷诺数的增大变化不大，并没有很强烈的雷诺数效应。

从图3(b)可以看出，在α=0°时，气动升力系数几乎为0。α=7°时，CL≈0～-0.15，方向向上，且随着Re的增大而绝对值逐渐增大。α=14°时，气动升力变化剧烈。在Re=0.89×105～1.77×105时，气动升力系数由0.49升至0.56，在Re=1.77×105～2.2×105时，气动升力急剧增大，由0.56增至1.13，并且在Re持续增大时，气动升力随之进一步增大，在试验Re=3.19×105时，气动升力系数达到了1.38。当α≥30°时，气动升力随着Re的变化不太明显，其中α=30°时气动升力为0.1，α=49°时约为0，α=90°时，气动升力在Re=0.89×105～2.2×105时由-0.3转为-0.2，此后趋于稳定。

为了进一步分析上述气动力随着雷诺数和风向角位置发生突变的原因，现进一步分析圆柱尾流风速的功率谱。

图4为平均气动力发生突变前后，当L/D=±1.94，T/D=0.5，即α=14°与166°时，圆柱B尾流区测点处风速功率谱。风速测点位置见图1，圆柱B的位置布置见图2。从图4可见，当雷诺数Re=177 248时，无论风速测点是位于下游圆柱的尾流区〔图4(a)〕还是位于上游圆柱的尾流区〔图4(c)〕，风速功率谱均没有明显峰值，即双圆柱绕流场中没有明显的漩涡脱落现象存在。而当雷诺数Re=265 872时，下游圆柱尾流风速功率谱〔图4(b)〕在St=0.12附近有一不大明显的峰值，而上游圆柱的尾流风速功率谱〔图4(d)〕则在St=0.43附近有一处非常明显的峰值，即在绕流场中存在明显的漩涡脱落。圆柱尾流风速功率谱的这种变化说明了当雷诺数从177 248增大至265 872时，双圆柱绕流场的流态结构发生了转变，从而导致了测力圆柱A上的气动力发生了不连续的跳跃现象(见图3)。

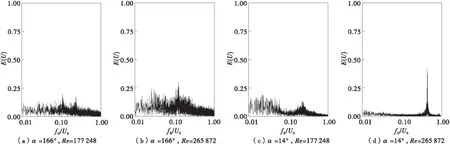
图4 双圆柱尾流风速功率谱Fig.4 Power spectra of wake flow velocity for twin cylinders

当α=14°时，可以看到气动阻力、升力变化剧烈。在Re=1.77×105～2.2×105时，气动升力急剧增大，由0.56增至1.13，与此同时，气动阻力急剧减小，由0.21减至-0.12。这一数值结果与文献[2]里Re=2.2×105时的数据也比较接近。这说明此时边界层处发生了“转捩”，延迟了尾流的分离，导致尾流区的宽度变窄，使得两剪切层的相互作用变强。此时，下游柱不再处于上游柱的尾流中，上游柱的尾流在两柱之间的间隙内流动，并且上游柱的剪切层高速侧再附于下游柱表面，导致升力急剧增大。这对应于顾志福等[2]IIB流态。图5分别为Re=177 248，265 872时下游柱的尾流风速时程曲线，由图5可见，在Re=177 248时，时程曲线的变化比较有规律，但是在Re=265 872时，时程曲线的变化不再有规律。这也说明当雷诺数Re从177 248增大至265 872时，流态发生了转变，从而正好对应于气动力在此时发生了不连续变化。

图5 Re=177 248，265 872时双圆柱尾流风速时程曲线Fig.5 Time-history curve of wake flow velocity for twin cylinders when Re=177 248 and 265 872

2.2 上游柱

相较于下游柱，上游柱的平均气动力变化并没有那么剧烈，图6为错列双圆柱上游柱气动力系数随雷诺数变化。

图6 错列双圆柱上游柱气动力系数随雷诺数变化Fig.6 Upstream aerodynamic coefficients of staggered double circular cylinders changing with Reynolds number

从图6(a)可以看出，在α=180°时，气动阻力约为0.9，比较稳定，同时雷诺数的变化不大。α=173°时，气动阻力随着雷诺数的升高有逐步下降的趋势，在Re=0.89×105～3.19×105气动阻力由1.05降为0.87。在α=166°时，气动阻力随着雷诺数的呈现先降后升的趋势，在Re=0.89×105～1.32×105时，阻力系数由0.86降为0.72。在Re=1.32×105～1.77×105时，阻力系数几乎不变，此时阻力系数达到最小值。在Re=1.77×105～3.19×105时，阻力系数随着雷诺数的升高而小幅上升，由0.72上升到0.79。在α=150°和131°时，阻力系数随着雷诺数的变化均几乎保持不变，α=150°时约为0.8，α=131°时约为0.87。

从图6(b)可以看出，在α=180°时，气动升力几乎为0。在小风攻角时，即90°<α≤150°时，上游柱的平均气动升力系数均≤0，约为0～-0.1，即双柱之间存在很小的斥力。在α=131°，Re=0.89×105～2.66×105时，升力系数随着雷诺数几乎没有变化，约为-0.1。在Re=2.66×105～3.19×105时，升力系数随着雷诺数的变化而急剧增大，由-0.07突升至0.97。当雷诺数进一步增大至3.28×105时，升力系数随之进一步增大至1.04，且有继续增大的趋势。但是，当风攻角降至90°时，升力系数又大致稳定在-0.3～-0.2，并无随着雷诺数增大而出现突变的现象。

为了进一步分析上述气动力随着雷诺数和风向角位置发生突变的原因，现进一步分析圆柱尾流风速的功率谱。图7为平均气动力发生突变前后，当L/D=±1.32，T/D=1.5，即α=49°与131°时，圆柱B尾流区测点处的风速功率谱。风速测点位置见图1，圆柱B的位置布置图见图2。

图7 双圆柱尾流风速功率谱Fig.7 Power spectra of wake flow velocity for twin cylinders

从图7可见，雷诺数Re=265 872时，下游圆柱的风速功率谱〔图7(a)〕在St=0.3附近有一不甚明显的峰值，而上游圆柱的风速功率谱〔图7(c)〕在St=0.31附近有非常明显的峰值，即在绕流场中存在明显的漩涡脱落。当雷诺数Re=319 046时，下游圆柱的风速功率谱〔图7(b)〕没有出现峰值，但是上游柱的风速功率谱〔图7(d)〕在St=0.41附近有非常明显的峰值。通过对比上游柱的风速功率谱发现，当雷诺数从265 872增大至319 046时，对应的St从0.31增大至0.41，这应该是双圆柱绕流场的流态结构发生了转变，从而导致了测力圆柱A上的气动力发生了不连续的跳跃现象(图5)。图8为雷诺数Re=265 872，319 046时上游柱的尾流风速时程曲线。

图8 Re=265 872，319 046时双圆柱尾流风速时程曲线Fig.8 Time-history curve of wake flow velocity for twin cylinders when Re=265 872 and 319 046

由图8(a)可见，在雷诺数Re=265 872时，尾流风速时程曲线变化颇有规律，但是当雷诺数Re=319 046时，尾流风速时程曲线变得不再规律，从而也可印证雷诺数从265 872增大至319 046时流态结构发生了变化。

3 结 论

笔者在雷诺数Re=0.9×105～3.2×105之间(涉及亚临界雷诺数和临界雷诺数)，利用风洞试验探究了近距离错列双圆柱的平均气动力系数及其随着雷诺数的变化规律，并探讨了其绕流场的流态结构和干扰机理。研究结论如下：

1)错列双圆柱的气动性能有强烈的雷诺数效应，在不同的风攻角下，临界雷诺数的圆柱平均气动力系数与亚临界区有很大差异。

2)对于下游圆柱，在临界雷诺数区域，当两圆柱处在某些相对位置时，平均气动升力与平均气动阻力均会同步随着雷诺数的增大而发生不连续的突变，这应该是发生了流态的转变。

3)对于上游圆柱，在临界雷诺数区域，当两圆柱处在某些相对位置时，上游圆柱会受到平均气动升力的作用，并且平均升力系数会随着雷诺数的变化发生不连续的突变。平均气动升力指向下游圆柱，即两柱之间产生了很大的吸力。这种气动力的突变很可能是双圆柱绕流场的流态结构的变化造成的。

[1] ZDRAVKOVICH M M. The effects of interference between circular cylinders in cross flow[J].JournalofFluidsandStructure,1987,1(2):239-261.

[2] GU Z F, SUN T F. On interference between two circular cylinders in staggered arrangement at high subcritical Reynolds numbers[J].JournalofWindEngineeringandIndustrialAerodynamic,1999,80(3):287-309.

[3] SUMNER D, PRICE S J, PAIDOUSSIS M P. Flow-pattern identification for two staggered circular cylinders in cross-flow[J].JournalofFluidMechanics,2000,411(1):263-303.

[4] PRICE S J, PAIDOUSSIS M P. The aerodynamic forces acting on groups of two and three circular cylinders when subject to a cross-flow[J].JournalofWindEngineeringandIndustrialAerodynamic,1984,17(3):329-347.

[5] ZDRAVKOVICH M M, PRIDDEN D L. Interference between two circular cylinders; series of unexpected discontinuities[J].JournalofIndustrialAerodynamics,1977(2):255-270.

[6] ALAM M M, MEYER J P. Global aerodynamic instability of twin cylinders in cross flow[J].JournalofFluidsandStructures,2013,41(8):135-145.

[7] ZHOU Y, FENG S X, ALAM M M, et al. Reynolds number effect on the wake of two staggered cylinders[J].PhysicsofFluids,2009,21(12):429-439.

[8] SUMNER D. Two circular cylinders in cross-flow: a review[J].JournalofFluidsandStructure,2010,26(1):849-899.

Reynolds Number Effect of Aerodynamic Forces of Close Range Parallel Cables of Cable-Supported Bridges

DU Xiaoqing1, ZHANG Liping1, LIU Qingkuan2, 3

(1. Department of Civil Engineering, Shanghai University, Shanghai 200072, P. R. China; 2. Wind Engineering Research Center, Shijiazhuang Tiedao University, Shijiazhuang 050043, Hebei, P. R. China; 3. Hebei Provincial Key Lab of Structural Health Monitoring and Control, Shijiazhuang 050043, Hebei, P. R. China)

Parallel cables with close range were used extensively in practical engineering. However, there were limited studies on the aerodynamics of parallel cables as well as their Reynolds number effects, especially at critical Reynolds regime. When Reynolds numbers were between 0.9×105～3.2×105, located in subcritical Reynolds regime and critical Reynolds regime, the aerodynamic characteristics of twin circular cylinders with close range along with their Reynolds numbers effect were investigated through a series of wind tunnel tests. Results show that the aerodynamic forces of two circular cylinders with close range have strong Reynolds number effect; with different wind attack angles, the average aerodynamic coefficients of circular cylinders in the critical regime are very different from those in subcritical regime. In the critical Reynolds number region, the mean lift coefficient of the downstream cylinder can reach more than 1.35, and the mean lift coefficient and drag coefficient suffer a discontinuous change with the change of Reynolds number, which may relate to the shift of the flow state. The mean lift coefficient of the upstream cylinder can reach more than 1.0, and the mean lift coefficient suffers a discontinuous change with the change of the Reynolds number, which may relate to the shift of the flow state of flow around twin circular cylinders.

bridge engineering; cable-supported bridge; wind tunnel test; flow around circular cylinder; Reynolds number effect

2015-09-04；

2016-03-06

上海市自然科学基金项目(14ZR1416000)；上海市教委科研创新项目(14YZ004)；国家自然科学基金项目(51578330)

杜晓庆(1973—)，男，江苏无锡人，副教授，主要从事桥梁和结构抗风方面的研究。E-mail：dxq@shu.edu.cn。

张利平(1990—)，男，湖北黄冈人，硕士，主要从事结构抗风方面的研究。E-mail：zhangliping_2014@126.com。

10.3969/j.issn.1674-0696.2016.06.01

U442.5

A

1674-0696(2016)06-001-05