两种模型在内陆无水港选址中的综合应用

梁承姬，嘉熲煚，徐德洪，鲁 渤

(1. 上海海事大学 物流研究中心，上海 201306；2. 西安外事学院 物流学院，陕西 西安 710000；3. 中国科学院大学 管理学院，北京 100049)

两种模型在内陆无水港选址中的综合应用

梁承姬1，嘉熲煚1，徐德洪2，鲁 渤3

(1. 上海海事大学 物流研究中心，上海 201306；2. 西安外事学院 物流学院，陕西 西安 710000；3. 中国科学院大学 管理学院，北京 100049)

从地理位置因素和经济因素两个不同的角度出发进行无水港选址研究，建立了集合覆盖模型和模糊聚类分析模型，并进行了实例分析，最后通过对两种选址模型的结果进行比较，确定了最佳的内陆无水港建设地，从而减少盲目建设，避免资源浪费，达到以最小的支出获得最大的利益的效果。

管理工程；无水港选址；集合覆盖模型；模糊聚类模型

0 引 言

无水港(Dry Port)，是相对于“有水港口”而言的，源自20世纪的欧美大陆。实际是指在内陆地区建立的具有报关、报验、签发提单等具有港口服务功能的物流中心。在无水港内设置有海关、检验检疫等监督机构为客户通关提供服务。同时，货代、船代和船公司也在无水港内设立分支机构，以便收货、还箱、签发以当地为起运港或终点港的多式联运提单，内陆的进出口商则可以在当地完成订舱、报关、报检等手续，将货物交给货代或船公司[1-3]。

无水港一般是通过公路和铁路集装箱运输与沿海港口相连接的，实现内陆集装箱货物的一次报关、一次放行，具备港口延伸功能、电子口岸功能、海关监管堆场功能、金融保险服务功能和保税功能等多项功能[1-3]。对于沿海港口来说，无水港的建设是一种增加货源、增强竞争力的有效手段，对于无水港所在城市而言，它有利于提高物流运作效率、促进经济增长、提升城市综合竞争力以及加快对外贸易，对于无水港附近的客户来说，可以在当地完成订舱、装箱、报关、放行、退税和保险等业务，提高了办事效率，也减少了物流成本。因此，内陆城市的无水港建设是港口未来的发展趋势，内陆城市则是港口竞相争夺的焦点。

内陆无水港建设是未来内陆城市发展的趋势，而对沿海港口来说如何在众多优势各异城市中选择最适合的城市作为建立内陆无水港的城市是其进行无水港业务拓展的首要问题。为了客观的分析候选城市，从而确定内陆无水港最佳的建设地点，这就必须对内陆无水港选址问题进行深入的研究。

1 内陆无水港选址研究国内外现状

世界各国的无水港实践情况、研究水平各不相同。欧美国家的内陆无水港发展比较早，相关研究较为丰富和系统，亚洲国家近年来内陆无水港也得到了快速发展，对内陆无水港的建设和研究日益重视。内陆无水港的选址研究与内陆集装箱集运站的选址研究具有一定的理论相似性，国外学者的理论基础是集装箱转运站的选址，我国学者的理论基础起步于铁路集装箱货运站的选址。

1.1 国外研究现状

学者B．J．C．M．RUTTEN[4]在内陆多式联运中转节点的范畴下展开多式联运网络研究，对内陆多式联运网络的发展、运输网络的布局、内陆节点选址等问题进行介绍。XU Yuanquan[5]提出了离散数学为基础的以营运赢利为目标函数的内陆集装箱的选址模型；G．BEMARD等[6]提出了建立双层顾客流的一个空箱站的选址模型；YANG Hua[7]应用多属性决策方法对美国德克萨斯州的内陆无水港选址问题进行了研究，给出了埃尔帕索地区的计算机模拟算例，并用多目标决策方法进行了内陆无水港投资决策研究，通过对内陆无水港的发展动力机制，内陆无水港选择的影响因素分析，以及各种不同选址方法的介绍比较，做了定量化的深入研究，并通过实例予以验证，为内陆无水港的建设布局等提供了理论基础。

J．WOXENIUS等[3]扩展了内陆无水港的概念，划分了内陆无水港的层次，定义了无水港的3种类型：远距离、中距离和近距离内陆无水港，建立内陆无水港可以减少港口城市的堵塞和调高内陆腹地的物流设施水平。

1.2 国内研究现状

朱晓宁[8]利用模糊聚类模型探讨全国集装箱货运站建设的等级、数量和地址。谢辉等[9]对铁路集装箱中心站的站址选择，提出基于变权法的多因素Fuzzy决策。

王红卫[10]首先分析了内陆无水港和集装箱货运站、堆场的区别，从货主的成本分析入手，利用离散选址理论推导和建立了内陆无水港选址模型；张兆民[11]讨论了无水港选址的原则(满足运输需求、整体、区域规划和追求经济效益)，从地区生成集装箱量和中转集装箱量两个方面入手提出了无水港选址布局影响因素，并以大连港口所依靠34个内陆腹地或潜在腹地为背景，根据模糊聚类方法进行无水港选址进行分析，然后和现有的无水港发展和规划进行对比。

杨睿[12]对内陆“干港”的选址进行了较为深入的研究，并提出基于DEA方法的选址模型以及利用模糊数学方法进行选址评测；邹伟宏[13]基于东北经济区域建立了内陆无水港遗传模糊聚类选址模型，从地区经济发展水平、地区交通运输环境、港口企业偏好3个角度设法对东北地区的内陆港进行选址研究；刘瀛寰[14]对内陆港选址可能带来的风险进行详细的分析，并将内陆港选址风险因素分为:运输需求风险、运输供给风险、政策环境风险、技术风险、经济风险5大类，并建立了内陆港选址风险因素的指标体系，并采用灰色模糊综合评价法进行内陆港选址风险进行综合评价；冯社苗[15]借鉴自然地理学的水系理论分析经济问题，通过对内陆无水港进出口物流成本影响分析，提出物流海拔和物流梯度的概念，并构建了物流海拔和梯度的计量模型。并且以中国大陆300多个城市的相关数据为依据，测算了中国大陆主要区域的物流海拔和梯度。

笔者在参考了上述文献的基础上，考虑了沿海港口经济腹地的货源城市以及潜在的货源城市的经济状况以及地理交通状况，建立了集合覆盖模型以及模糊聚类分析模型，综合应用到内陆无水港选址问题中，运用lingo进行求解，分析得出最佳选址结果。

2 模型的构建

2.1 选址的影响因素

选址问题的影响因素通常可以分为：地理因素、经济因素、政治因素、交通因素、社会因素和自然因素等。经济因素是指在候选点设置设施后，与从该设施提供服务或商品所需成本相关的因素，通常包括交通运输成本、人力资源、土地价格等。交通因素指内陆无水港候选址通常在交通运输能力较强、具备发达的集疏运网络的地方。社会因素指的是社会环境、社会治安、居民生活水平、生活习惯等。自然因素指的是气候条件、水资源状况、地理条件等[16]。

一般来说，物流中心应该建立在能产生大量适箱货物的地区，特别是在一些交通的交汇点或依托铁路或公路而建的枢纽点，这些地区的商贸交易活跃，并且经济条件良好，对货物运输的需求量大。针对无水港自身的特性，还要考虑无水港与依托港之间的交通的便利性。笔者以内陆城市的经纬度数据以及是否处于高速铁路节点等的地理位置因素作为集合覆盖模型的指标依据来确定候选城市。内陆无水港选址属于经济设施选址，通常以经济效益作为选址目标，所以笔者以经济因素指标作为模糊聚类模型的指标依据来选择建设无水港的城市。其他影响因素由于评价指标体系数据不全或存在不确定性，暂不考虑。

2.2 集合覆盖模型

覆盖模型是一种求解对于需求已知的一些节点，确定一套服务设施以服务这些需求节点的数学方法[17]。根据求解方法的不同，可以分为两种模型：第1种是集合覆盖模型，这种方法用最少的服务设施去服务所有的需求节点；第2种是最大覆盖模型，这种方法事先已知设施的数量，即用固定设施数量去服务尽可能多的需求节点。

2.2.1 模型的构建

由于本选题所研究的无水港的数量是未知的，因此采用集合覆盖模型更适合本选题的分析[10]。集合覆盖模型如下：

(1)

(2)

(3)

yij≥0, i∈N,j∈M

(4)

(5)

式中：N为n个需求点的集合，N={1,2,3,…,n}；M为m个候选设施节点集合，M={1,2,3,…,m}；di为第i个需求节点的需求量；Cj为设施节点j的容量；A(j)为设施节点j所服务的需求点集合；B(j)为服务需求节点i的设施节点j的集合，B(j)={j|i∈A(j)}；yij为节点i的需求中由设施节点j提供服务的部分，yij≤1；xj为节点j是否被选中成为服务设施，如果被选中xj=1，否则xj=0。

式(1)是目标函数，表示模型的目标是被选为设施节点的数量最小；式(2)是约束条件，确保所有需求节点的需求都得到完全满足；式(3)是约束条件，是对每个设施的服务能力的限制；式(4)是约束条件，允许一个设施为某个需求提供部分需求。

2.2.2 实例分析

笔者选取兰州到上海海铁联运支干线上的主要货源城市或潜在的货源城市为研究对象，进行无水港选址研究。

1)用经纬度数据计算样本城市之间的距离

以内陆城市的经纬度数据以及是否处于高速铁路节点来确定无水港的候选城市，理想的候选城市有：宝鸡、西安、洛阳、郑州、武汉、合肥、南京、襄樊、成都、重庆、徐州、蚌埠、贵阳、南昌。

以候选城市的经度和纬度数据作为原始数据(表1)，为降低复杂度，我们假设候选城市处于同一水平面上，即忽略地球的球形特征以及各城市之间的海拔差异，应用欧氏距离法计算候选城市两两间的距离，计算公式为：

式中：x和y分别表示城市的经度和纬度，计算结果见表2。

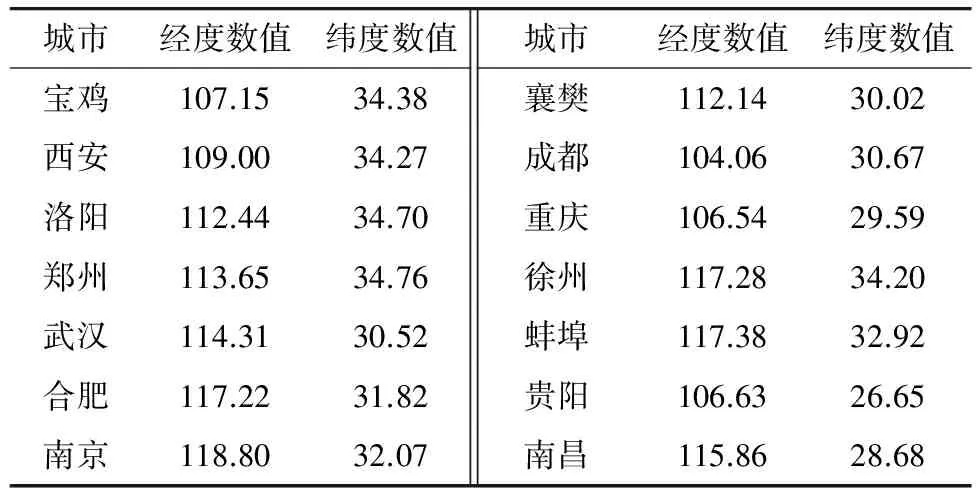
表1 候选城市的经纬度数据

表2 候选城市的距离矩阵

2)确定无水港候选城市的辐射范围

根据距离矩阵确定样本城市的辐射范围，从地理位置上看，以武汉为中心向东可以辐射到合肥和南京地区，北面可以辐射到郑州、洛阳等地，向南可以辐射到株洲、南昌等地。其中，南京是这几个城市中距离武汉相对较远的，直线距离约为546 km，因此本选题以南京到武汉的距离为本模型的辐射距离，根据表2中的距离矩阵，可以计算出每个候选城市的辐射城市，见表3。

表3 候选城市的辐射范围

Table 3 Radiation range of candidate cities

候选城市辐射范围宝鸡x1宝鸡，西安西安x2宝鸡，西安，洛阳，郑州，成都洛阳x3西安，洛阳，郑州，武汉，成都郑州x4西安，洛阳，郑州，武汉，合肥，襄樊，成都，徐州埠武汉x5洛阳，郑州，武汉，合肥，南京，襄樊，成都，重庆，徐州，蚌埠，贵阳，南昌合肥x6郑州，武汉，合肥，南京，襄樊，徐州，蚌埠，南昌南京x7武汉，合肥，南京，徐州，蚌埠，南昌襄樊x8郑州，武汉，合肥，襄樊，成都，重庆，贵阳，南昌成都x9西安，洛阳，郑州，武汉，襄樊，成都，重庆重庆x10武汉，襄樊，成都，重庆，贵阳徐州x11郑州，武汉，合肥，南京，徐州，蚌埠蚌埠x12郑州，武汉，合肥，南京，徐州，蚌埠，南昌贵阳x13武汉，襄樊，重庆，贵阳，南昌南昌x14武汉，合肥，南京，襄樊，蚌埠，贵阳，南昌

3)集合覆盖模型求解

根据表3，令：

i=1,2,3,…,14。

根据以上集合覆盖模型求解，结果如表4。

表4 选址结果

根据模型的求解结果可知，最优解X={0,1,0,0,0,1,0,0,0,1,0,0,0,0}，最优目标函数值为3。根据最优解可知，按照地理位置作为选址依据，只要在候选城市中建立3个无水港就能覆盖所有的候选城市，这3个无水港分别为西安、合肥和重庆。

2.3 模糊聚类模型分析

聚类是指按照事物间的相似性进行无监督的分类，而聚类分析则是运用数学方法设定一定的规则，是研究对象自动归类。传统的聚类分析采用硬划分的方法，把每个待识别的研究对象严格地归到某个类中，是一种非此即彼、界限分明的分析方法。而实际生活中，大多数研究对象并没有严格的分界点，而是有一定的过度区间，因此出现了软划分方法，即模糊聚类分析[8,11,18]。

2.3.1 模型的构建

模糊聚类分析的目的是把n个样本划分到c个类别中，使各样本与其所在类均值的误差平方和最小，即使准则函数式(6)最小：

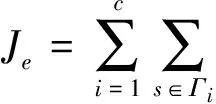
(6)

式中：mi为第i类的样本均值；s∈Гi为分类到i类的所有样本。

式(6)最小化的基本方法是C均值法，模糊C均值聚类模型构造过程如下：

设样本集为X={x1,x2,…,xk, …,xN}，第i个类别为Si(1,2,…,c)，对于元素xk，记ωik=ωSi(xk)为元素xk属于类别Si的隶属度。

假设对于给定的一个整数c(2≤c≤n)，满足：

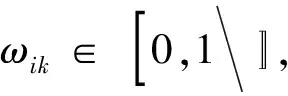
(7)

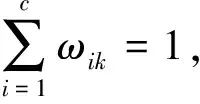
(8)

(9)

那么，模糊矩阵W=[ωik]c×n是一个模糊C划分，记为：Mfc={所有X上的模糊C划分}

则模糊C均值聚类分析模型为：

(10)

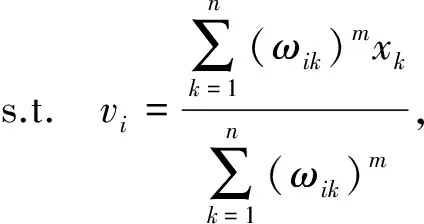
(11)

W∈Mfc

(12)

笔者采用模糊等价矩阵的方法对模糊C均值聚类模型进行求解，具体步骤如下：

1)先通过标准差法对原始数据进行标准化，公式为：

(13)

2)标准化后根据欧氏距离法建立模糊相似矩阵，公式为：

R=[rij]n×m

(14)

(15)

式中：m为样本指标个数；c为可使0≤rij≤1的一个常数，i,j=1,2,…,n是样本的个数。

构造了模糊相似关系矩阵后，可以求解模糊等价矩阵，将模糊相似关系矩阵进行先取小后取大的合成运算，停止准则为Rk=R2k，满足停止准则时的模糊矩阵就是模糊等价矩阵。在模糊等价矩阵中设定分类临界值θ，即可对样本实现聚类。

2.3.2 实例分析

模糊聚类模型分析选取反映城市当前发展状况的指标，主要是影响无水港选址的因素，包括国内生产总值、固定资产投资额、工业总产值、社会消费品零售总额、具有一定规模的企业数、批发零售贸易业总额，实际利用外资额、货物运输总量和外贸进出口总额9项指标[19-21]，分别用X1～X9表示，见表5。

整理数据，对表5中的原始数据进行标准化处理，使其具有相同的数量级。根据求解模糊C均值聚类模型的求解步骤，首先分别计算各项指标的均值和标准差，然后根据标准化式(13)计算出标准化后的数据矩阵，得到该矩阵后，按式(14)和式(15)求解模型的模糊相似矩阵，将模糊相似矩阵自乘，此处略去自乘过程中得到的自乘矩阵，经过16次自乘后，第一次出现Rk=R2k，即R8=R16。根据停止准则，此时自乘停止，得到的模糊矩阵即为模糊等价矩阵，则模糊等价矩阵是R8，见表6。

表6 模糊等价矩阵

根据模型计算结果中的模型等价矩阵(表6)可知，按照临界值θ取值的不同，样本城市的聚类结果如下：

当θ=0.58时，可以将候选城市分为2类，重庆自成一类，其余城市组成一类：{(宝鸡,西安,洛阳,郑州，武汉,合肥,南京,襄樊,成都,徐州,蚌埠,贵阳,南昌),重庆}；

当θ=0.76时，可将候选城市分为3类，重庆和南京分别自成一类，其余城市组成一类：{(宝鸡,西安,洛阳,郑州,武汉,合肥,襄樊,成都,徐州,蚌埠,贵阳,南昌),重庆,南京}；

当θ=0. 81时，可将候选城市分为4类，重庆、南京和成都分别自成一类，其余城市组成一类：{(宝鸡，西安,洛阳,郑州,武汉,合肥,襄樊,徐州,蚌埠,贵阳,南昌),重庆,南京,成都}；

当θ=0.84时，可将候选城市分为5类，重庆、南京和西安分别自成一类，武汉和成都组成一类，其余城市组成一类：{(宝鸡,洛阳,郑州,合肥,襄樊,徐州,蚌埠,贵阳,南昌),(武汉,成都),重庆,南京,西安}；

当θ=0.95时，候选城市分为10类：{(宝鸡，蚌埠),西安,(洛阳,郑州,合肥),(成都,武汉),南京,(襄樊，贵阳),重庆,徐州,南昌}。

根据模糊聚类的结果，最先从候选城市中独立出来的城市是重庆，然后依次是南京、成都、西安和武汉。

2.4 两种模型的结果分析

如表7从地理位置角度考虑，通过集合覆盖模型求得的选址结果是西安、合肥和重庆，从社会综合效益角度出发，通过模糊聚类分析求得的选址结果是重庆、南京、成都、西安和武汉。两种选址模型分析的角度不同，但分析得出的结果有共同的偏好，即西安和重庆。如果确定内陆无水港建设城市为两个时，应首选西安与重庆，此结论与实际建设相符合，证明了其方法的可行性。

表7 两种模型结果分析

3 结 语

笔者选取兰州到上海海铁联运支干线上的主要货源地或潜在的货源地所在的14个城市作为实际算例，运用两种选址模型从不同角度对其进行分析。集合覆盖模型不考虑候选城市的经济社会条件，只根据地理位置的分布进行选址，而模糊聚类模型则不考虑候选城市所处的地理位置，根据实际需要构建评价指标进行选址。两种无水港选址模型的分析结果不完全一致，但有共同偏好，因此，结合两种选址模型的分析结果，综合运用到无水港选址中，能充分避免无水港重复建设的问题，有效提高无水港选址的准确性，减少资源浪费，能大大地增强内陆无水港设施的利用率，为社会带来更多的经济效益。也证明了两种模型综合选址的优越性，确保选址结果更加客观准确，保证在既定付出的基础上得到充分的利用。

[1] RODRIGUE J P,DEBRIE J,FREMONT A,et al.Functions and actors of inland ports:European and north American dynamics [J].JournalofTransportGeography,2010,18(4):519-529.

[2] Andrius Jaržemskis,VASILIAUSKAS A V.Research on dry port concept as intermodal node [J].Transport,2007,22 (3):207-213.

[3] ROSO V,WOXENIUS J,LUMSDEN K.The dry port concept:connecting seaports with their hinterland [J].JournalofTransportGeography,2009,17(5):338-345.

[4] RUTTEN B J C M.The design of a terminal network for inter modal transport [J].TransportLogistics,1998,1(4):279-298.

[5] XU Yuanquan.ADiscreteChoiceBasedFacilityLocationModalforInlandContainerDepot.[D].Morgantown,West Virginia,USA:West Virginia University,1999.

[6] BERNARD G,JEAN-YVES Potvin.A tuba search with slope scaling for the multi-commodity capacitated location problem with balancing requirements [J].AnnalsofOperationsResearch,2003,122(1/4):193-217.

[7] YANG Hua.InlandPortLocationModelUnderTransTexasCorridorConcept[D].Texas,USA:The University of Texas,2005.

[8] 朱晓宁.集装箱货运站选址的模糊聚类模型与算法[J].运筹与管理,2004,13(5):91-94. ZHU Xiaoning.Fuzzy clustering model and algorithm for built place of container freight station [J].OperationsResearchandManagementScience,2004,13(5):91-94.

[9] 谢辉,盖宇仙.多因素模糊决策在集装箱中心站选址中的应用[J] .铁道运输与经济,2006,28(1):73-75. XIE Hui,GAI Yuxian.Fuzzy decision-making among multi-factors for location-choosing of container center station [J].RailwayTransportandEconomy,2006,28(1):73-75.

[10] 王红卫.“无水港”建设及离散选择理论在选址中的应用[D].上海:上海海事大学,2004. WANG Hongwei.DryPortConstructionandDiscreteChoiceTheoryintheApplicationoftheLocation[D].Shanghai:Shanghai Maritime University,2004.

[11] 张兆民.模糊C-均值聚类在内陆无水港选址中的应用[J] .上海海事大学学报,2008,29(4):34-38. ZHANG Zhaomin.Applying fuzzy C-clustering to location planning of dry port [J].JournalofShanghaiMaritimeUniversity,2008,29(4):34- 38.

[12] 杨睿.内陆干港及其选址研究[D].上海:上海海事大学,2006. YANG Rui.InlandDryPortanditsLocationStudy[D].Shanghai:Shanghai Maritime University,2006.

[13] 邹伟宏.东北地区内陆港选址规划研究[D].大连:大连海事大学，2009. ZOU Weihong.StudyonInlandPortLocationPlanningofNorthwestChina[D].Dalian:Dalian Maritime University,2009.

[14] 刘瀛寰.内陆港选址风险评价模型研究[D].大连:大连海事大学,2010. LIU Yinghuan.TheStudyonEvaluationModelofRiskofInlandPortLocation[D].Dalian:Dalian Maritime University,2010.

[15] 冯社苗.基于物流海拔理论的枢纽陆港布局研究[J].北京交通大学学报,2011,10(1):23-28. FENG Shemiao.Study on location of hub inland port based on logistics elevation theory [J].JournalofBeijingJiaotongUniversity,2011,10(1):23-28.

[16] ROBINSON A E.Inland ports and supply chain management [C]//Mexico:International Business Association’s 8thAnnual Conference,1999.

[17] 姜阳光,庞大钧.基于集合覆盖模型的城市ULS物流节点选址分析[J].物流科技,2009(10):54-55. JIANG Yangguang,PANG Dajun.Analysis on locations for urban ULS logistics links based on set covering model [J].LogisticsSci-tech,2009(10):54-55.

[18] 高新波.模糊聚类分析及其应用[M].西安:西安电子科技大学出版社,2004:31-40. GAO Xinbo.FuzzyClusteringAnalysisandItsApplication[M].Xi’an:Xidian University Press,2004:31-40.

[19] 宋吉成.基于模糊C-均值聚类分析的青岛无水港选址研究[D].青岛:中国海洋大学,2011. SONG Jicheng.ResearchontheLocationofQingdaoPort’sDryPortBasedonFuzzyC-MeansClustering[D].Qingdao:Ocean University of China,2011.

[20] 李芳,史小宁,胡昊.基于二项logit的无水港选址影响因素分析及预测[J].重庆交通大学学报(自然科学版),2012,31(5):1046- 1049. LI Fang,SHI Xiaoning,HU Hao.Analysis of influencing factors and location prediction of dry port based on logit model [J].JournalofChongqingJiaotongUniversity(NaturalScience),2012,31(5):1046-1049.

[21] 邵静静.内陆无水港的选址与集疏运系统的优化研究[D].重庆:重庆交通大学,2014. SHAO Jingjing.StudyoftheLocationoftheInlandDryPortandOptimizationofConsolidationandDistributionSystem[D].Chongqing:Chongqing Jiaotong University,2014.

Comprehensive Application of Two Kinds Models in Inland Dry Port Location

LIANG Chengji1, JIA Jiongjiong1, XU Dehong2, LU Bo3

(1. Logistics Research Center, Shanghai Maritime University, Shanghai 201306,P.R.China; 2. Logistics Institute, Xi’an International University, Xi’an 710000, Shaanxi,P.R.China; 3. School of Management, University of Chinese Academy of Sciences, Beijing 100049,P.R.China)

The dry port location problem was studied from two different perspectives, such as the geographical factors and economic factors, and a set covering model and a fuzzy clustering model were established. And the case study was also carried out. Finally, through comprising the results of the two kinds of location models, the optimum location of the inland dry port was determined, which reduced the blind construction, avoided the waste of resources, and achieved the maximum benefit with the minimum expenditure.

management engineering; dry port location; set covering model; fuzzy clustering model

2014-10-21；

2014-12-08

国家自然科学基金项目(71471110,71301101)；中国博士后科学基金项目(2014M550084)

梁承姬(1971—)，女(朝鲜族)，吉林龙井人，教授，博士，主要从事物流系统运作计划与优化、口岸物流流程模拟与重组、港口布局优化与模拟、港口安全工程等方面的研究。E-mail:xionglong210@126.com。

10.3969/j.issn.1674-0696.2016.01.34

U169.6;U651+.5;F252; F272

A

1674-0696(2016)01-177-07