基于相对熵模型的交通安全设施比选方法研究

赵晓华，李佳辉，万钰涵，荣 建

(1. 北京工业大学 城市交通学院，北京 100124；2. 重庆市勘测院，重庆 400021)

基于相对熵模型的交通安全设施比选方法研究

赵晓华1，李佳辉1，万钰涵2，荣 建1

(1. 北京工业大学 城市交通学院，北京 100124；2. 重庆市勘测院，重庆 400021)

合理设置交通安全设施是保障交通安全的重要措施之一，但存在较多设施评估比选问题。不同的决策者在选择设施方案时，往往依据个人偏好对方案评价指标的重要性进行判断。由此得到的指标权重向量具有方案倾向性，导致方案之间的竞争是不公平的。为解决此问题，选取北京市学校地区作为案例，综合考虑学校地区的安全性、驾驶员的舒适性、设施的成本等因素，利用驾驶模拟实验获取85th速度差、加速度标准差等作为方案的评价指标。并利用相对熵模型对不同专家给出的评价指标权重进行集结，求得对所有方案而言公平民主的权重向量。利用该权重向量和加权平均模型得到方案的综合评价值，最终得到方案的优劣排序，为决策者选择方案提供理论依据。

交通运输工程；交通安全设施；学校地区；方案比选；相对熵模型

0 引 言

学校地区作为交通安全重点保护区域近年来引起了社会各界的广泛关注。有研究表明交通安全设施不健全是导致学校地区交通安全问题的重要原因之一[1]，因此，合理设置交通安全设施是保障学校地区交通安全的重要措施。无论是我国GB5768—2009《道路交通标志和标线》还是美国的《交通控制设施一致性手册》(MUTCD)都对学校地区标志标线的使用进行了详尽的说明和规定。目前，我国北京等各大城市也将各种标志标线投入了实际应用，取得了一定的效果。但目前对于学校地区各种标志标线的有效性，以及各种标志标线组合设置方案的有效性并不是十分明确。特别是哪种方案更有利于提高学校地区的交通安全值得深入讨论，以支持实际应用。为了比选评估各种设施组合方案的有效性，在方案比选过程中引入了效能权重系数这一指标。权重系数是指在一个领域中，对目标值起权衡作用的数值。权重系数可分为客观权重系数和主观权重系数。客观权重系数是指经过对实际发生的资料进行整理、计算和分析，从而得出的权重系数，例如标准离差法和CRITIC法，这类方法研究较晚，且很不完善，尤其是计算方法大多比较繁琐，不利于推广应用。主观权重系数(又称经验权数)是指人们对分析对象的各个因素，按其重要程度，依照经验，主观确定的系数，例如专家评分法、Delphi法、AHP法。这种方法人们研究的较早，也较为成熟，但个人主观倾向性较大[2-3]。

综合对比主、客观权重系数的特点，鉴于主观权重系数确定方法的简便性及可实施性，笔者以主观权重系数为出发点，为了消除方案评价指标权重确定过程中出现的专家意见的个人倾向性，构建了方案评价指标权重计算的相对熵模型求解方案评价指标的权重。由此得到的权重向量满足广泛性、一致性、无关方案独立性、民主性以及非独裁性等性质，即对所有方案而言，是一种公平民主的权重向量，进而对方案的比选提供了平等的竞争基础[4]。

1 研究对象选取及数据采集

为了说明基于相对熵模型的交通安全设施比选方法的应用，以北京市小学地区为例，采用现状调查与问卷调查相结合的方式，并参考学校地区相关法律法规，最终选取与学校地区相关的1种交通标线及5种交通标志作为研究对象，如表1。并选取具有代表性的“光明小学”作为具体实例进行研究。

表1 学校地区相关交通标志标线

实地调查结果表明，90%的学校都设有学校地区宣传提示标志和学校地区注意儿童标志，因此在方案设计时以2种标志作为基础设施，其他4种设施在基础设施的前提下进行设置，形成4种不同的设施设置方案，方案编号记为ai,i=1，2，3， 4。将基于相对熵模型确定4种设计方案评价指标的权重，进而对各方案进行比选。

为了避免其他因素之间的交互影响，更好的控制实验条件，节约实验成本，利用驾驶模拟实验测试以上4种设施设置方案。4种方案中的设施分别设置在光明小学门前的道路上，形成4条实验道路，实验道路随机排列，并且两两之间由500 m左右的过渡段连接，最终形成一条封闭的实验场景。驾驶模拟实验过程中，选取30位驾驶员作为实验被试。正式实验前被试进行试驾，以熟悉驾驶模拟车辆的操作装置。正式实验时，被试从实验场景中的任意一点出发，并严格控制实验过程，驾驶模拟器将记录被试车辆运行状态，包括速度、加速度等参数。将采集的30位被试的行为状态数据作为本文进一步研究的数据基础。

2 评价指标选取及归一化处理

选取方案评价指标时，以学校地区的交通安全为重点，兼顾驾驶员减速过程中的舒适性，并考虑设施的设置成本，选取以下3项指标作为方案的评价指标，记为C=(C1,C2,C3)：

C1：85th速度差，设施设置前与设置后85th速度之差，反映驾驶员的减速程度，数值越大表明减速程度越明显；

C2：加速度标准差，相应方案下的加速度标准差，反映驾驶员减速过程中的行驶平稳性，数值越小表明行驶越平稳；

C3：设施的成本，成本数据由北京市公安局公安交通管理局交通设施管理处提供。

对于以上评价指标中的85th速度差和加速度标准差，截取30位被试第一刹车点与校门口之间的速度和加速度数据(设施设置方案影响范围内的数据)进行预处理，经过缺失值处理及噪声数据处理，获得27位被试的有效数据。由27组有效的速度及加速度数据计算85th速度差和加速度标准差，得到的评价指标决策矩阵如表2。

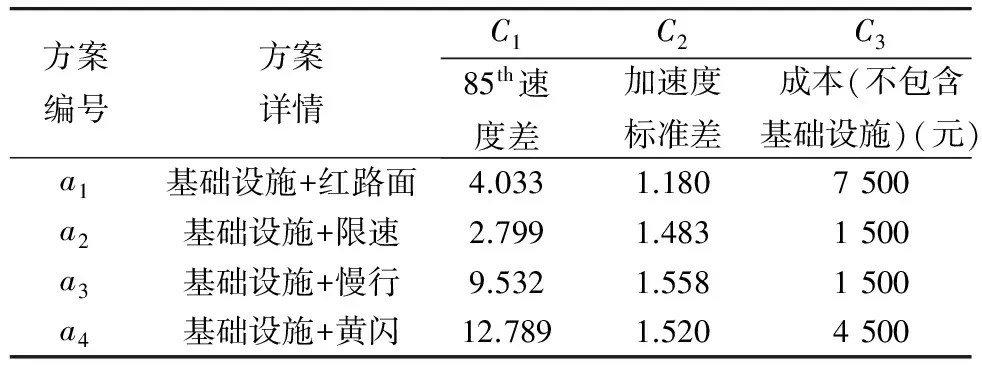
表2 评价指标决策矩阵

以上3项评价指标由效益型评价指标和成本型评价指标两类构成。由于各个评价指标具有不可公度性和矛盾性，首先要对评价指标决策矩阵进行规范化处理[5-6]。

对于方案在效益评价指标下的评价值(i=1，2，…，m)，进行如下规范化处理：

(1)

对于方案在成本评价指标下的评价值(i=1，2，…，m)，进行如下规范化处理：

(2)

经过规范化得决策矩阵Y=(yij)m×n，其中0≤yij≤1，i=1，2，…，m；j=1，2，…，n。

定义表2中的85th速度差为效益型评价指标，加速度标准差和设施成本为成本型评价指标，按照式(1)和式(2)将决策矩阵进行归一化处理，得到规范化的决策矩阵Y：

3 基于相对熵模型的方案评价指标权重确定

3.1 相对熵模型简介

为了得到方案优劣的排序，文中采用加权平均综合评价模型，得出方案的综合评价值，值越大说明方案的优越性越明显。加权平均综合评价模型是指被判别方案的所有评价指标的得分与其自权重乘积的和，其数学表达式为[7]：

(3)

式中：di为方案ai的综合评价值；yij为归一化后方案ai在评价指标cj下的评价值；wgj为评价指标cj的权重系数；m为方案的个数；n为评价指标的个数。

由于每位专家给出的评价指标的权重系数不同，即权重系数代表了决策者的一种偏好。而利用相对熵模型得到的权重向量满足广泛性、一致性、无关方案独立性、民主性以及非独裁性等性质，故选取相对熵集结方法能够求得对所有方案而言公平民主的群权重向量。结合相对熵模型的概念，要获得专家群体对评价指标C的群偏好向量Wg，就要最小化它与每个专家给出的评价指标重要性偏好向量的相对熵，建立方案评价指标权重计算的相对熵模型如式(4)：

(4)

由式(4)可知，通过计算各个专家对方案评价指标重要性的个人偏好向量与群偏好向量之间偏离值的最小值，使得各位专家对方案评价指标重要性的个人偏好与群偏好之间进行比较，最后通过求解此模型，可以得到专家群体对方案评价指标集合C=(c1,c2，c3)的群偏好向量Wg[8]。

求解相对熵模型的最优解，首先对方案评价指标的评判矩阵Z进行归一化处理，如式(5)，归一化处理后得到矩阵B：

(5)

最终求得相对熵模型(4)的最优解，即为方案评价指标的群偏好向量Wg=(wg1,wg2,…,wgj)T：

1.2 纳入与排除标准 纳入标准：①符合手术适应证；②于本院行麦默通微创旋切术；③患者及其家属自愿配合心理干预行为。排除标准：①合并精神障碍或有精神疾病史者；②近期发生重大生活事件者。③合并其他重大疾病者。

(6)

3.2 方案评价指标权重确定

对于现有的4个备选方案a1，a2，a3，a4确定其方案属性的有3个评价指标c1,c2,c3。召集4位专家对方案进行评价，每个专家依据个人经验对方案评价指标的重要性进行评判，得到评判矩阵Z：

矩阵Z中的数据越大，表示该专家认为这项属性越重要。

利用公式(5)对评价矩阵Z标准化，得到归一化矩阵B：

由矩阵B可知，每位专家对方案评价指标重要性的个人偏好是不一样的，而且有的还相差很大，笔者通过求得专家群体对方案评价指标重要性的群偏好来解决这一问题。

假设参与方案决策的4位专家的权重是相同的，即We1=We2=We3=We4=0.25，专家的具体权重可根据实际情况而定。

以此类推，求得3个方案属性的群偏好权重Wg=(0.378，0.242，0.380)T。

4 学校地区交通安全设施比选

群偏好权重有效避免了专家个人的方案倾向性，使各方案具有平等的竞争基础。由群权重向量Wg及方案的决策矩阵Y，利用加权平均综合模型(3)最终得到4种方案的综合评价值：

d1=0. 378×0.14+0.242×0.30+0.380×

0.09=0.155

d2=0. 378×0.09+0.242×0.24+0.380×

0.39=0.244

d3=0. 378×0.33+0.242×0.23+0.380×

0.39=0.328

d4=0. 378×0.44+0.242×0.23+0.380×

0.13=0.272

由上述方案综合评价值可知，方案综合评价结果的顺序为d3>d4>d2>d1，即根据4位决策专家的综合意见，最终选择方案a3(基础设施+慢行标志)作为设置方案。

由此得到的评价结果反映了专家群体的倾向性，会因决策专家的不同而不同。因此专家评分环节对于方案最终效能评价的结果起到了关键的作用，所以，在方案评价过程中，为了使评价结果更合理更具代表性，需扩大决策专家专业的广度及专家的数量。

5 结 语

以北京市光明小学为例，说明相对熵模型在交通安全设施效能评价中的应用。通过驾驶模拟实验获取驾驶员的客观数据作为设施有效性的评价指标，并针对决策专家对不同评价指标给予的权重，利用相对熵模型对权重进行集结，有效避免了专家个人的方案倾向性，得到对于每种方案均公平的群权重向量。进而计算各方案的综合评价值，最终得到各方案综合评价值的大小排序，为决策者选择方案提供了理论支持。

笔者只选取4种方案、3项评价指标为例简要说明相对熵在设施比选过程中的应用。实际应用中，相对熵模型对于多方案多评价指标的比选评价仍然有效。希望通过此案例的说明，提出有效消除专家个人倾向性的方法，为交通安全设施设置方案效能评价提供理论依据。

[1] ALBERT R,DOLGIN K D.Lasting effects of short-term training on preschoolers’ street crossing behavior [J].AccidentAnalysisandPrevention,2010(42):500-508.

[2] 王晖,陈丽,陈垦,等.多指标综合评价方法及权重系数的选择[J].广东药学院学报,2007,23(5):583-589. WANG Hui,CHEN Li,CHEN Ken,et al.Multiple index comprehensive evaluation and the choice of weight coefficient [J].JournalofGuangdongCollegeofPharmacy,2007,23(5):583-589.

[3] 王宝亮,陈洪凯.熵权决策法在滑坡治理方案优化选择中的应用[J].重庆交通大学学报(自然科学版),2009,27(6):1112-1114. WANG Baoliang,CHEN Hongkai.Application of entropy weight decision making method to the optimal selection of landslide treatment scheme [J].JournalofChongqingJiaotongUniversity(NaturalScience),2009,27(6):1112-1114.

[4] 齐照辉,张为华,范玉珠.一种新型的多属性决策权重计算方法[J].运筹与管理,2006,15(3):20-24. QI Zhaohui,ZHANG Weihua,FAN Yuzhu.A new algorithm of weight coefficients of multiple attribute decision making [J].OperationsResearchandManagementScience,2006,15(3):20-24.

[5] 聂静涛,徐枞巍,孙昭旭.基于满意度的多指标决策模型及其在员工绩效评价中的应用[J].西安石油大学学报(自然科学版),2007,22(3):127-129. NIE Jingtao,XU Zongwei,SUN Zhaoxu.Multi-criteria decision-making model based on satisfactory degree and its application in performance assessment [J].JournalofXi’anShiyouUniversity(NaturalScience),2007,22(3):127-129.

[6] 刘晓佳,孔祥臣,施其洲,等.交互式权重优化法在路网规划方案综合评价中的应用[J].重庆交通学院学报,2006,25(5):136-138. LIU Xiaojia,KONG Xiangchen,SHI Qizhou,et al.The optimizing method of alternating weighting applying in the road net planning synthetical estimation [J].JournalofChongqingJiaotongUniversity,2006,25(5):136-138.

[7] 黄柳倩.加权平均型综合评价模型在成绩排序中的应用[J].第一健身俱乐部:理论研究,2010,4(7):32-34. HUANG Liuqian.The application of weighted average of the comprehensive evaluation model in score sorting [J].FitnessClubTheoreticalStudy,2010,4(7):32-34.

[8] 徐亚军,吴浩,刘庆禄.多属性决策中方案属性权重计算的相对熵模型[J].指挥控制与仿真,2012,34(5):18-20. XU Yajun,WU Hao,LIU Qinglu.The relative entropy model for calculation of program attribute weight in multiple attributes decision-making [J].CommandControl&Simulation,2012,34(5):18-20.

Program Selection of Traffic Safety Devices Based on Relative Entropy Model

ZHAO Xiaohua1, LI Jiahui1, WAN Yuhan2, RONG Jian1

(1. College of Metropolitan Transportation, Beijing University of Technology, Beijing 100124,P.R.China; 2. Chongqing Survey Institute, Chongqing 400021,P.R.China)

One of the most important measures to improve the traffic safety is to reasonably install traffic safety devices, but there are many problems in the evaluation and selection of the devices. Different decision-makers often judge the importance of the evaluation index of the program according to their personal preferences in the choice of devices. Therefore, the weight vector of the index has a plan tendency, and the competition among the schemes is not fair. In order to solve the problem, a case study on the traffic safety devices around school zone in Beijing was carried out, and factors such as 85thspeed difference and standard deviation of acceleration obtained by simulation test were selected as evaluation indicators of the program, with the comprehensive consideration of the safety of school zone, the comfortableness of drivers, the cost of devices and etc.. The relative entropy model was used to aggregate the weight of evaluation indicators given by different experts; therefore, the weight vector which was fair and democratic for all the programs was obtained. Finally, by using the obtained weight vector and the weighted average model, the comprehensive evaluation value of the program was obtained and the ranking of the programs was also obtained, which could offer theoretical foundation for decision-makers to select the program.

traffic and transportation engineering;traffic safety devices; school zone; program selection; relative entropy model

2014-10-09；

2014-12-02

国家自然科学基金项目(51108011)

赵晓华 (1971—)，女，山西太谷人，教授，博士，主要从事交通信息与控制、驾驶行为与安全、交通仿真等研究方面的工作。E-mail：zhaoxiaohua@bjut.edu.cn。

10.3969/j.issn.1674-0696.2016.01.32

U491.5

A

1674-0696(2016)01-167-05