环氧沥青混合料的疲劳行为研究

黄 明

(1. 上海市政工程设计研究总院(集团)有限公司，上海 200092；2.同济大学 道路与交通工程教育部重点实验室，上海 201804)

环氧沥青混合料的疲劳行为研究

黄 明1,2

(1. 上海市政工程设计研究总院(集团)有限公司，上海 200092；2.同济大学 道路与交通工程教育部重点实验室，上海 201804)

以美国ChemCo环氧沥青为例，按马歇尔设计方法进行了混合料设计，利用万能材料试验机MTS-81完成疲劳试验，并对沥青混合料小梁力学特性进行了检测，从沥青用量、摊铺等待时间、应力比3个影响因素，分析了环氧沥青混合料疲劳性能的变化规律，并回归了环氧沥青混合料的疲劳行为方程。结果表明：疲劳寿命与沥青用量、摊铺等待时间、应力比3个影响因素的关系分别为：随应力比增大而减小，随沥青用量的增大而增大，越过某个特定的时间点之后随摊铺等待时间的增大而减小，疲劳寿命的以10为底的对数分别与3个因素呈幂函数、指数和指数关系；提出多维拟合后的疲劳行为预估方程；并经过验证，此方程的适用范围限于应力比在0.3～0.7以内，沥青用量在5%～8%以内，以及摊铺等待时间在0～120 min以内。

道路工程；环氧沥青混合料；小梁试验；疲劳行为

0 引 言

环氧沥青混合料从1961年使用以来较广泛的使用在钢桥面铺装上，大多出现了早期损坏，直接影响到行车的安全性、舒适性、耐久性等，这与其疲劳有很大的关系。从上世纪60年代起，疲劳性能检测是美国、德国、日本的研究及桥面铺装规范中所涉及的检测项目之一[1]。国外对钢桥面铺装用的环氧沥青混合料的疲劳性能研究开展的较早，C.T.METCALF等[2]和F.F.FONDRIEST等[3]均采用复合梁对环氧沥青混合料进行了弯曲疲劳试验，并以普通沥青混合料为对比，得到环氧沥青混凝土在抗疲劳性能方面远优于普通沥青混凝土的结论；W.HAIFANG[4]提出基于间接拉伸试验的黏弹性分析沥青混合料疲劳性能；K.A.GHUZLAN[5]用耗散能方法来分析沥青混合料疲劳特性，然而这些方法所选取的因素太少，不足以从全方面反映环氧沥青混合料的疲劳性能。

环氧沥青国产化之后，国内专门针对桥面铺装层进行的疲劳性能方面的研究陆续开始，黄卫等[6]利用复合梁进行了大量的应变控制的疲劳试验，试验中以应变量为变量，且应变量都在很小的范围内<200 εμ，认为国产环氧沥青混合料疲劳性能优异；并对钢桥面铺面结构层进行了多方面的力学分析佐证了这一结论，从静态的力学分析角度探讨了铺装层裂缝产生的原因，并给出了简单的预防措施；然而影响沥青混合料疲劳性能的不仅仅在于应变量，还包括沥青用量、空隙率、施工质量等等。根据作者此前的研究，环氧沥青混合料施工要求严苛，铺面的空隙率和质量主要受摊铺等待时间的影响[7]，再者在大型钢桥面的铺装中，沥青面层的疲劳破坏主要源自受到钢桥面底部带来的弯拉应力，只有在上述几种影响因素下的疲劳性能变化才有参考价值，因此提出环氧沥青铺面材料的疲劳行为的预估方程对桥面铺装的设计、施工和维护具有十分重要的意义[8]。为此，本次研究将从多因素全面设计的基础上进行环氧沥青混合料的疲劳性能研究。

1 试验材料与前期

石料的选择：粗集料(≥2.36 mm)与细集料(0.075～1.18 mm)都采用玄武岩，产地为江苏溧阳，矿粉是由石灰石研磨而成，产地为浙江吉安，其表观密度为2.788 g/cm3。集料的基本性能的测试结果见表1。

表1 集料性能指标

环氧沥青选用美国ChemCo环氧沥青，它曾成功的应用在SanMetreo和金门大桥上[9]，具有广泛的代表性。沥青混合料级配范围选取南京长江二桥用级配，通过筛分出级配中值用于试验，这种级配在我国后来的许多新建大型钢桥的桥面铺装上均有应用[10]，级配如表2。

表2 环氧沥青混合料级配

混合料制备过程如下：沥青B组分(沥青与固化体系的混合物)加热至115 ℃备用，A组分(环氧树脂)加热至90 ℃备用，石料保温130 ℃，环氧沥青混合料拌和温度为120 ℃，AB组分在拌锅内混合，矿粉常温加入。

每个沥青用量下成型马歇尔试件3个，按规程进行马歇尔试件体积计算。不同沥青用量下的混合料体积参数与马歇尔试验结果如表3。

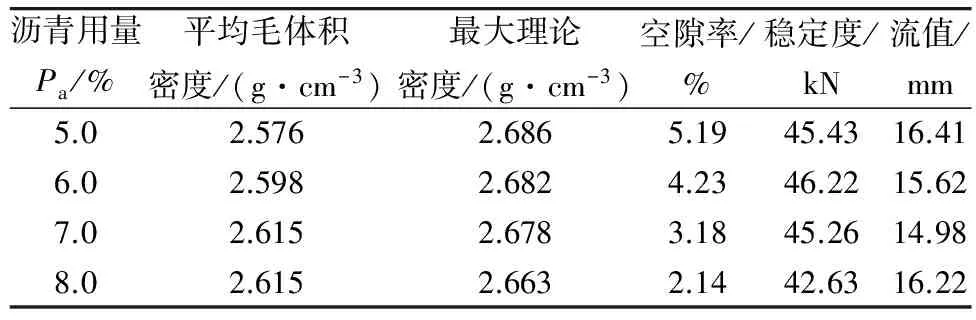
表3 不同沥青用量对应的空隙率

2 疲劳试验

2.1 试件的成型与小梁试件的力学特征

依据我国规范[11]选取了轮碾法成型混合料试件，使用车辙试验模具，尺寸为：300 mm×300 mm×50 mm，然后进行切割，切割成小梁尺寸为200 mm×50 mm×50 mm，误差为±2 mm。通过MTS-810试验机，使用中点加载模具，图1为夹具和施加应力示意图。由于不同沥青用量(Pa)和不同摊铺等待时间(T1)下的混合料的性质是不一样的，试验对不同影响因素的小梁进行单次最大弯拉应力测试，试验环境温度为15 ℃。

图1 中点加载疲劳试验夹具和力学示意Fig.1 Fatigue test fixture of midpoint load and its mechanic schematic diagram

首先通过其抗弯拉强度可计算出其抗弯拉应力σ，再进行不同应力比下的疲劳试验。除考虑应力比外，还加入沥青用量和摊铺等待时间来表征影响其疲劳性能的变量。参数中Pa表示沥青用量，Tw表示摊铺等待时间，下同。最大弯拉应力试验结果如表4。

表4 不同内部影响因素下的沥青混合料小梁力学特征

Table 4 Mechanical characteristics of epoxy asphalt mixture beam under influence of different internal factors

沥青含量Pa/%Tw/min最大压力PB/kN抗弯拉应力σ/MPa跨中挠度d/mm最大弯拉应变ε/(×10-3)弯曲劲度模量SB/MPa5．004．3410．4160．17521．31407926．94304．3610．4640．17331．29988050．78604．4510．680．17881．34107964．21904．119．8640．16111．20838163．871203．237．7520．15321．14906746．746．004．5510．920．21221．59156861．45304．5310．8720．23281．74606226．8604．6211．0880．22151．66136674．49904．149．9360．19231．44236889．241203．187．6320．18251．36885575．897．004．1810．0320．25221．89155303．73304．2310．1520．26141．96055178．27604．2210．1280．25231．89235352．36904．019．6240．21131．58486072．881203．167．5840．20041．50305045．918．004．1810．140．27661．89154303．73304．2310．320．27141．96054278．27604．2210．420．27131．89234252．36904．019．380．25231．58484572．881203．167．180．22511．50304145．53

分析表5中的弯曲劲度与沥青用量、摊铺等待时间的关系，可绘制出图2、图3的关系。

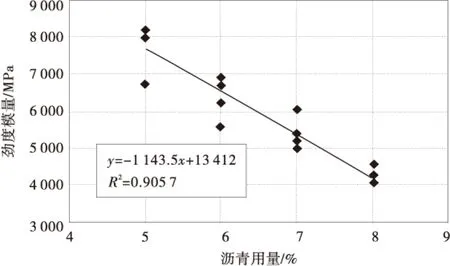
图2 劲度模量随沥青用量变化Fig.2 Stiffness modulus changing with asphalt content

图3 劲度模量随摊铺等待时间变化Fig.3 Stiffness modulus changing with paving waiting time

从图2、图3可以看出，劲度模量SB与沥青用量有着很好的线性关系，但与摊铺等待时间的变化的关系并不是很明显，总体略呈下降趋势。

应力疲劳试验方案：我国规范[11]中容许拉应力指标采用的是15 ℃的参考值，参照国内外的研究成果，本次小梁弯曲疲劳试验采用15 ℃作为试验温度；加载频率为10 Hz，半正弦波。荷载大小选取0.3，0.5，0.7 三个倍数作为试验变量，即指σt/σ。

选取4种沥青用量，即5%，6%，7%和8%；另外对于环氧沥青，摊铺等待时间是特别需要重视的因素，它影响着环氧沥青混合料的路用性能，也是一个综合指标[12]。另外空隙率在许多研究中都被列为了一个影响因素，但在矿料级配一定的情况下，空隙率的形成主要由沥青用量和施工质量决定的，摊铺等待时间能够综合反映施工质量，所以在本次环氧沥青混合料的研究中不单列空隙率作为一个影响因素。

试验采用全面设计，全面设计表见表5。接下来的叙述中，将应力比范围0.3～0.7倍，沥青用量范围5%～8%，以及摊铺等待时间范围0～120 min，总称为“既定条件范围”。

表5 全面设计

疲劳破坏判断标准为：小梁完全断裂，即MTS传感器中力的数值出现大幅下降的时刻为止。

2.2 疲劳试验结果

由于是模拟大型钢桥面的铺装，采用的是应力控制，再者混合料小梁的稳定度很高，说明其具有很大的刚度，故疲劳试验结束条件选取以梁的完全断裂为标准。从图4可以清晰的看出，试验结束后小梁已完全破坏，并且表现出十分刚性的破坏。

图4 小梁疲劳破坏正面Fig.4 Front view of beam fatigue crack

根据既定设置，记录整个试验过程的混合料疲劳破坏次数，试验数据如表6。

表6 疲劳试验结果

Table 6 Results of fatigue test

3 试验结果的分析与疲劳行为方程

3.1 单一因素的影响

根据试验结果，分别按3个应力比、4个沥青用量和5个摊铺等待时间与疲劳次数(Nf)的单对数做散点关系图，并采用最小二乘法对各个指标与疲劳次数的关系进行了多项式、幂函数、指数函数以及对数函数的曲线拟合，得到最大的曲线相关系数的曲线分别如图5。

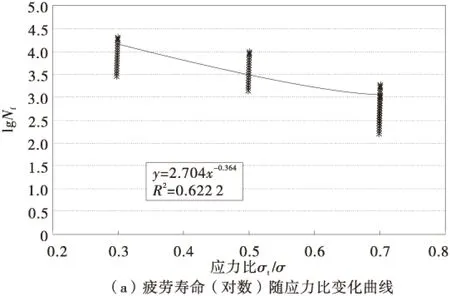
图5 疲劳寿命(对数)的变化曲线Fig.5 Curve of fatigue life (logarithm)

虽然3个曲线的相关系数并不是很高，但这是由于同一横坐标下的变量过多造成，故这并不影响曲线的拟合的大致走势，若将数值取平均，会得到较好的相关系数。从上面3条曲线可以看出，疲劳寿命的以10为底的对数与应力比呈幂函数关系，与沥青用量、摊铺等待时间都呈指数关系，则疲劳寿命也与之呈相应的关系，则可初步判断其疲劳寿命随应力比增大而减小，随沥青用量的增大而增大。值得注意的是，图7中，存在一个最佳的摊铺等待时间tx，在这个时间点之前，疲劳寿命基本变化不大，越过某个特定的时间点tx之后随摊铺等待时间的增大而减小。关于tx的研究，研究者在文献[7]中有较为详细的论述。

3.2 疲劳方程的回归

对比J.HARVEY等[13]对控制应变疲劳试验结果得到的回归方程，其方程在单因素(沥青用量、空隙率和应变大小)下的拟合关系分别为指数、指数、幂的关系，与本次研究得到的关系类似，基于此将由本次研究的3种单因素整合到一个公式中进行多维拟合，建立如式(1)的回归方程：

(1)

式中：x1,x2,x3,x4,x5分别为待定的参数；Nf为疲劳寿命，次；σt/σ为应力比，无量纲；Pa沥青用量，%；e为自然对数。

将表6的研究结果中所有数据输入1stOpt编程软件中，通过既定的回归公式，拟合得到各个参数，在后来的研究中，实施证明此类方程是比较有效的预估混合料疲劳寿命的方程形式。结果如式(2)：

R2=0.931

(2)

式中:Tw为摊铺等待时间，min。

可见沥青混合料疲劳寿命与应变水平、沥青用量以及摊铺等待时间有较好的相关性，总体而言，在“既定条件范围”内，应力比越小，沥青用量越大，摊铺等待时间不超过某个特定的值则疲劳寿命越长。式中的相关系数较高，这是由于Harvey在选取方程式经过了回归细化，将相关因素的取值范围作了一定的限定，且在多因素综合影响下，多组数据达到此消彼长的效果，相关度会相对提高。

4 行为方程的验证

作为疲劳行为方程，就应该具有预估疲劳的功能。由于笔者进行的试验量即小梁疲劳试验仅在100余次，为验证其准确性和一般性，以下按同样的方法成型小梁，设计了12组非常规点(其中包括7组超出“既定条件范围”)作为疲劳方程的验证试验，试验条件、参数和验证结果如表7。

表7 验证试验结果

Table 7 Verification of test results

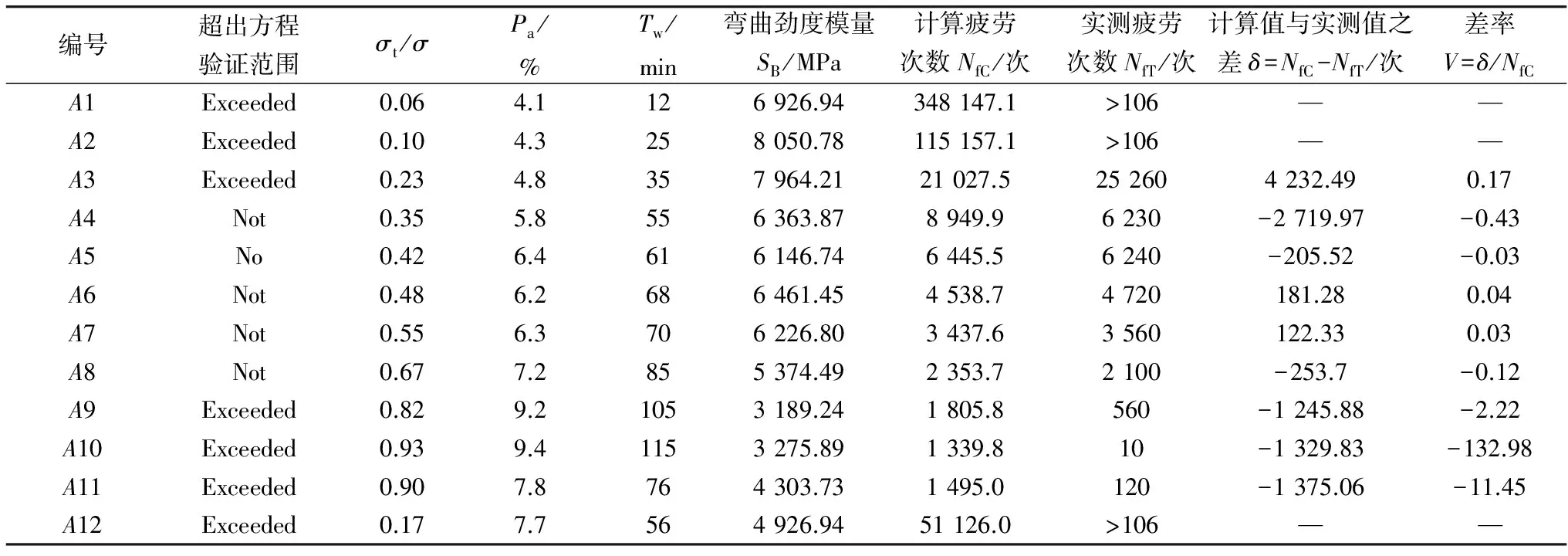
编号超出方程验证范围σt/σPa/%Tw/min弯曲劲度模量SB/MPa计算疲劳次数NfC/次实测疲劳次数NfT/次计算值与实测值之差δ=NfC-NfT/次差率V=δ/NfCA1Exceeded0．064．1126926．94348147．1>106——A2Exceeded0．104．3258050．78115157．1>106——A3Exceeded0．234．8357964．2121027．5252604232．490．17A4Not0．355．8556363．878949．96230-2719．97-0．43A5No0．426．4616146．746445．56240-205．52-0．03A6Not0．486．2686461．454538．74720181．280．04A7Not0．556．3706226．803437．63560122．330．03A8Not0．677．2855374．492353．72100-253．7-0．12A9Exceeded0．829．21053189．241805．8560-1245．88-2．22A10Exceeded0．939．41153275．891339．810-1329．83-132．98A11Exceeded0．907．8764303．731495．0120-1375．06-11．45A12Exceeded0．177．7564926．9451126．0>106——

从表7的差率值可以看出，大部分超出了“既定条件范围”(应力比范围0.3～0.7倍，沥青用量范围5%～8%，以及摊铺等待时间范围0～120 min)的小梁疲劳寿命与计算值相差很远，仅有黑体字表示的A3号试件验算结果尚可接受。这是由于在很低(﹤0.2)的应力比和较高的沥青用量的情况下，环氧沥青混合料的疲劳性能十分优异，MTS试验机极限疲劳加载次数为保护仪器而不允许过高的数值，使得环氧沥青混合料的室内疲劳寿命根本无法测得，并且沥青用量如果太高也会超出混合料的空隙率下限；其次，在应力比很高(>0.8)的情况下，试验机与夹具之间的应力集中会导致具有高模量的环氧沥青混合料发生瞬间脆断，而这种脆断不属于疲劳破坏的范畴；相反，没有超出“既定条件范围”的小梁试件的疲劳试验具有很好的复现性。

综合以上验证的情况可以看出，若将其方程推广开来，需进行如下的限定，即式(2)仍只适用于“既定条件范围”之内的疲劳次数预估。

5 结 论

1)环氧沥青混合料具有很高的劲度模量，经过初步试验亦验证了应变控制疲劳试验是不可取的。

2)环氧沥青混合料小梁的力学性质方面，抗弯拉应力与沥青用量的变化的关系不显著，劲度模量SB与沥青用量有着很好的线性关系。

3)提出了3个影响疲劳性能的因素，疲劳寿命与应力比、沥青用量以及摊铺等待时间，他们与疲劳性能的关系分别为：随应力比增大而减小，随沥青用量的增大而增大，越过某个特定的时间点tx之后随摊铺等待时间的增大而减小，其10为底的对数与3个因素分别呈幂函数，指数和指数关系。

4)多维拟合后的疲劳行为方程为Nf=2.412×102.442×e0.144Pa-0.007T1×(σt/σ)-2.044，并经过验证，此方程的适用范围为应力比在0.3～0.7以内，沥青用量在5%～8%以内，以及摊铺等待时间在0～120 min以内。

[1] 黄卫,刘振清.大跨径钢桥面铺装设计理论与方法研究[J].土木工程学报,2005,38(1):53-59. HUANG Wei,LIU Zhenqing.Research on theory and method of long span steel bridges deck surfacing design [J].ChinaCivilEngineering,2005,38(1):53-59.

[2] METCALF C T.Flexural of paving materials for orthotropics seel plate bridge [J].HighwagResearchRecord,1967:54-60.

[3] FONDRIEST F F,SNYDER M J.Addendum report paving practices for wearing surfaces on wearing surfaces on orthotropic steel bridge decks [J].Am-IronSteelInst.:SteelResearchandConstructionBulletin,1971,10(20):20-26.

[4] WANG Haifang.FatiguePerformanceEvaluationofWesTrackAsphaltMixturesBasedonViscoelasticAnalysisofIndirectTensileTest[D].Raleigh:North Carolina State University,2002:12-23.

[5] GHUZLAN K A.FatigueDamageAnalysisinAsphaltConcreteMixturesBasedUponDissipatedEnergyConcepts[D].Urbana-Champaign,US:University of Illinois at Urbana-Champaign,2001:22-25.

[6] 黄卫,钱振东,程刚,等.大跨径钢桥面环氧沥青混凝土铺装研究[J].科学通报,2002,47(24):1894-1897. HUANG Wei,QIAN Zhendong,CHENG Gang,et al.Epoxy asphalt concrete paving on the deck of long-span steel bridges [J].ChineseScienceBulletin,2002,47(24):1894-1897.

[7] 黄明,黄卫东.摊铺等待时间对环氧沥青性能影响研究[J].建筑材料学报,2012,15(1):122-125. HUANG Ming,HUANG Weidong.Study on impaction of paving waiting time on performance of epoxy asphalt mix [J].JournalofBuildingMaterials,2012,15(1):122-125.

[8] 黄明.考虑多因素的沥青混合料疲劳性能评价与对比[D].上海:同济大学,2013. HUANG Ming.EvaluationandComparisonofFatiguePerformanceofAsphaltMixtureConsideringMultipleFactors[D].Shanghai:Tongji University,2013.

[9] READ J,WHITEOAK D.TheShellBitumenHandbook[M].London:Thomas Telford,Ltd,2003:78-112.

[10] 魏奇芬,张晓春,王森.大跨径钢桥桥面沥青铺装设计之比较[J].江苏交通,2003(12):49-51. WEI Qifen,ZHANG Chunxiao,WANG Sen.Comparison of design methods of asphalt pavement of large scale steel bridge [J].JiangsuTransportation,2003(12):49-51.

[11] 交通部公路科学研究院.公路工程沥青及沥青混合料试验规范:JTG E20—2011[S]北京:人民交通出版社,2011. Research Institute of Highway Ministry of Transport.StandardTestMethodofBitumenandBituminousMixturesforHighwayEngineering:JTG E 20—2011 [S].Beijing:China Communications Press,2011.

[12] 交通部公路科学研究院.公路沥青路面施工技术规范:JTG F40—2004 [S].北京:人民交通出版社,2004. Research Institute of Highway Ministry of Transport.TechnicalSpecificationforConstructionofHighwayAsphaltPavements:JTG F40—2004[S].Beijing:China Communications Press,2004

[13] HARVEY J,DEACON J,TSAI B,et al.FatiguePerformanceofAsphaltConcrete[R].California,USA:Asphalt Research CAL/APT Program,1995:42-47.

Research on Fatigue Behavior of Epoxy Asphalt Mixture

HUANG Ming1, 2

(1. Shanghai Municipal Engineering Design Institute (Group) Co.,Ltd., Shanghai 200092, P.R.China; 2. Key Laboratory of Road and Traffic Engineering of the Ministry of Education, Tongji University, Shanghai 201804, P.R.China)

Taking American ChemCo epoxy asphalt mixture for example, the mixture was designed according to the Marshall Design method. The fatigue test was completed by universal material testing machine MTS-81 and the beam mechanic characteristics of asphalt mixture were tested. The variation law of fatigue performance of epoxy asphalt mixture was analyzed from 3 influence factors, including asphalt content, paving waiting time and stress ratio. Finally, a fatigue behavior equation of epoxy asphalt mixture was regressed. The results show that the relationship between the fatigue life and asphalt content, paving waiting time and stress ratio three factors is as follows: fatigue life decreases when the stress ratio increases; it increases when the asphalt content increases; it decreases when the waiting time increases after passing a particular time point. The logarithm of the fatigue life taking 10 as bottom presents as a power function, index and index relationship with the three factors respectively. The equation turns out after multi-dimensional fitting. Through verification, the equation can be applied when the stress ratio is between 0.3 ～ 0.7, the asphalt content is between 5% ～ 8% and the paving waiting time is within 0～120 min.

highway engineering; epoxy asphalt mixture; beam tests; fatigue behavior

2014-12-01；

2015-03-04

住房和城乡建设部科学技术计划项目(2014-K1-025)；上海市政总院科研项目(K2014K028)

黄 明(1985—)，男(侗族)，湖北恩施人，高级工程师，博士后，主要研究方向为新型道路路面材料和结构的研发与评价。E-mail:huangming@smedi.com。

10.3969/j.issn.1674-0696.2016.01.09

U414

A

1674-0696(2016)01-046-05