无轴承同步磁阻电机转子径向位移自检测技术

徐恩翔，朱熀秋

(江苏大学，镇江 212013)

无轴承同步磁阻电机转子径向位移自检测技术

徐恩翔，朱熀秋

(江苏大学，镇江 212013)

为确保无轴承同步磁阻电机(BSRM)稳定运行，需要对转子位置进行实时控制，则需使用相关传感器(如电涡流传感器)检测转子径向的偏心位移信号。为降低无轴承同步磁阻电机控制系统的成本，缩减电机的长度与体积，可以移除位移传感器。提出了一种基于电感矩阵模型的无轴承同步磁阻电机无位移传感自检测技术。通过建立与分析精确模型，设计出无轴承同步磁阻电机的转子位移观测器，并基于MATLAB/Simulink仿真软件构建电机转子径向位移自检测控制系统，对所提出的理论进行仿真实验研究。仿真试验结果表明：该方法能准确有效地预测转子的偏心位移。

无轴承同步磁阻电机；电感矩阵；无位移传感；自检测

0 引 言

随着社会的发展以及科技的进步，高速化机床的需求量与日俱增，为实现电机的高速化可靠运转，就必须解决轴承带来的磨损问题。传统机械轴承接触高速转动轴，故有需润滑、寿命短、维护成本高等弊端，这大大限制了电机向高速、超高速方向发展[1]。无轴承电机具有无摩擦、无磨损、无需润滑、高速高精等优点，可用于生命科学、化学化工等领域。除了上述优点外，由于无轴承同步磁阻电机的转子上无励磁绕组或永磁体，所以其结构简单、成本低廉，而且转子为凸极结构，故可实现较高的凸极比，因此无轴承同步磁阻电机(以下简称BSRM)具有低转矩脉动、高转矩密度、低损耗、高功率因数等性能优点，与其他类型的无轴承电机相比，更加适用于高速高精的领域[2-3]。在传统BSRM控制中，转子的偏心位移量一般由电涡流传感器来检测，这势必会增加电机控制系统的成本，增大电机的体积；且传感器对工作环境有一定的要求，因此无法适用于恶劣的环境中，这将大大限制BSRM的发展。因此研究转子径向位移无传感自检测技术对BSRM运行控制具有重大的研究价值和应用前景。

1 基于电感矩阵的BSRM数学模型

无轴承电机的电感模型对研究无轴承电机的径向悬浮力数学模型、动态特性与高精度解耦控制有着举足轻重的作用，因此建立适用于无轴承电机的精确电感矩阵模型至关重要。本文选择转矩绕组(Na，Nb)为4极，悬浮力绕组(Nα，Nβ)为2极，且转子凸极宽度为2ρ的BSRM作为研究对象，其结构如图1所示。

如图1所示，将4极转矩绕组的b相绕组与2极悬浮力绕组的β相绕组的轴线重合于α-β坐标系的α轴线上。假设电机使用在空间上按正弦分布的集中式绕组，且仅仅考虑基波绕组的情况下，将

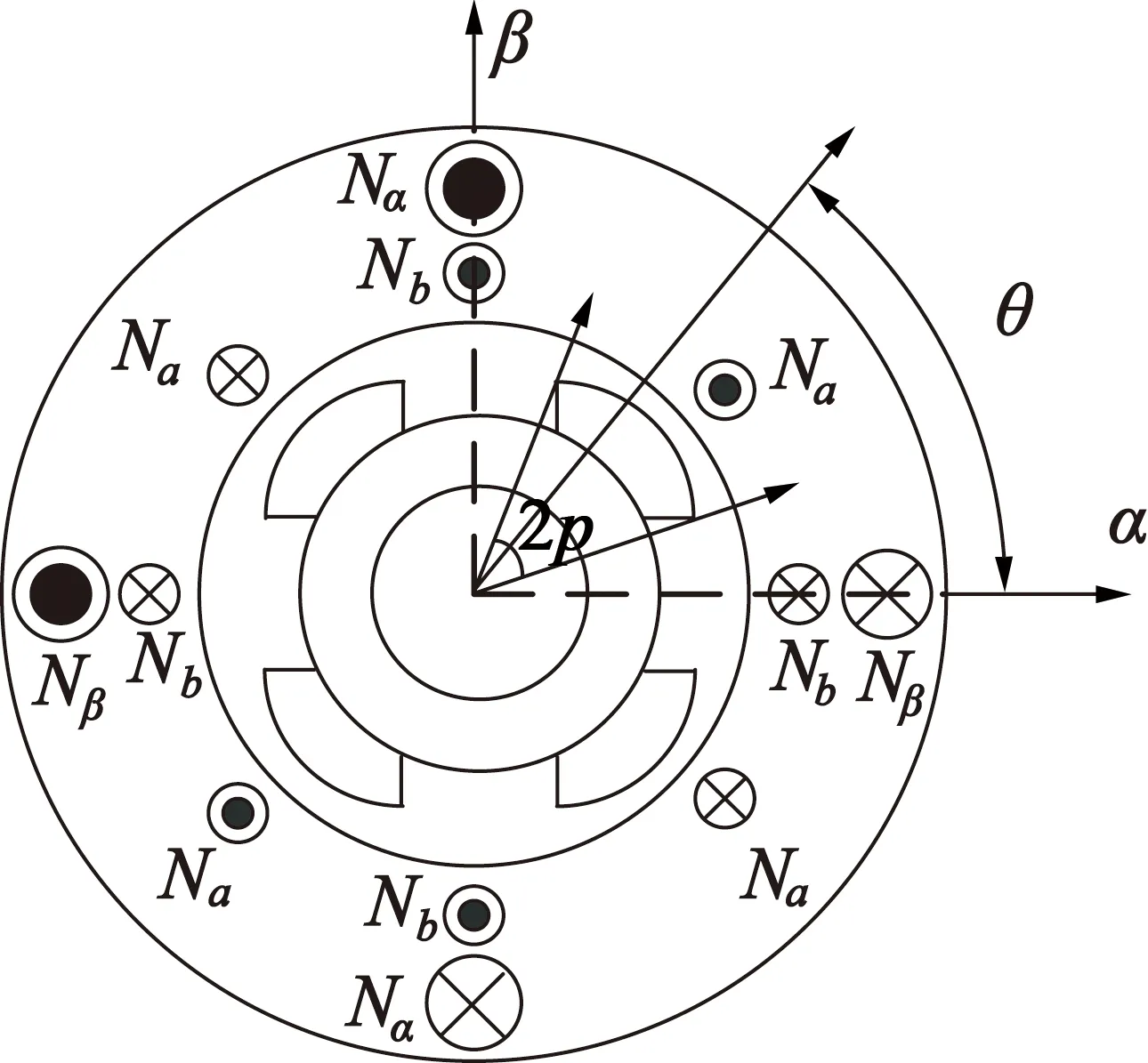
图1 无轴承同步磁阻电机绕组分布图

各绕组用傅里叶级数分解，可得出绕组沿气隙圆周的匝数分布[4-5]：

(1)

式中：K为基波幅值，是数值为4/π的常数；θ为空间机械角度；W4，W2分别为转矩绕组与悬浮力绕组的每相串联有效匝数。

电机转子主要有圆柱型与凸极型两种基本类型，BSRM虽采用凸极型转子结构，但圆柱型转子结构属于凸极型转子结构的特例，故本文以圆柱型转子结构为例对转子偏心位移做研究对象。图2为转子偏心示意图。图中，O(0,0)为转子无偏移时中心

图2 转子偏心示意图

位置坐标；O'(x,y)为转子偏移时中心位置坐标；θ为电机实际转过的机械角度；x，y分别表示转子偏移量在α轴、β轴上的分量。设转子外表面与电机定子内径的单边平均气隙长度为g0，转子外表面与电机定子内径的单边气隙长度为g(θ)，由转子偏心引起的气隙变化值为Δg，则电机的转子单边气隙长度表达式：

(2)

假设电机气隙长度远远大于转子的偏心位移量，则转子偏心位移量可忽略不计，则气隙长度g(θ) 的倒数可表示：

(3)

由式(2)、式(3)可得转子表面dθ弧度内的气隙磁导率分布函数：

(4)

式中：μ0为空气磁导率；r为转子半径；l为转子铁心长度。

如果转子结构为凸极，则凸极区域与非凸极区域的气隙显然是不等的，则当计算气隙磁导率时需将两者相加。但是由于非凸极区域的气隙长度要比凸极区域的气隙长度大得多，因而非凸极区域的气隙磁导率也就比凸极区域的气隙磁导小得多，为简化计算，可忽略非凸极区域的气隙磁导率，将其视为零。则考虑凸极转子结构的气隙磁导率时，只需将转子凸极区域的部分代入式(4)中计算即可。其中凸极区域可表示：

(5)

由于在电机运行时，径向悬浮力等于磁场储能对转子径向位移的偏导数，而电感储能直接反映了磁场的储能状况，在计算电感时必须考虑由于转子偏心所引起的磁通变化。假设在α相绕组中通入的电流大小为iα，忽略电机磁路产生的压降，则沿转子表面dθ弧度内产生的气隙磁通：

(6)

式中：Fα为悬浮力绕组α相的转子磁位。

由高斯定律可知，则磁通沿气隙圆周的积分应等于0，则结合式(1)、式(4)与式(6)可得悬浮力绕组α相的转子磁位：

(7)

同理可得悬浮力绕组β相、转矩绕组a相与b相的转子磁位：

(8)

结合式(6)～式(8)可得在转子偏心后气隙沿dθ弧度的磁通分布：

(9)

由式(9)可看出，当转子发生偏心时，4极转矩绕组的磁通分布不会发生改变；而2极悬浮力绕组的磁通会随转子偏心位移量的变化而变化，具体表现为指向产生转子偏心位移方向上的气隙磁压降减少，而背离方向上的气隙磁压降增加。

2 转子位移观测器

在旋转坐标系下，定义电流矢量：

(10)

式中：电机转矩绕组的电流为i1d，i1q；悬浮力绕组的电流为i2d，i2q。

旋转坐标系下，电机转矩绕组的自感矩阵：

(11)

旋转坐标系下，电机悬浮力绕组的自感矩阵：

(12)

旋转坐标系下，电机两相绕组的互感矩阵：

(13)

式(11)～式(13)中各电感系数计算式如下：

(14)

由上式推导出的BSRM的电感模型，可求出电机转矩绕组气隙磁链在两相旋转坐标系下的分量：

(15)

将式(11)、式(12)、式(13)代入式(15)中，可得：

(16)

将式(16)解方程，可得d，q轴的位移分量hd，hq：

(17)

将式(17)经过2r/2s变换，可得出转子在α，β轴位移分量x，y：

(18)

由式(17)可知，根据电感矩阵模型的推导，转子径向位移量可通过测量电机两套绕组的电流计算得出，从而实现BSRM的无位移传感技术。因此准确求得电机转矩绕组的磁链ψ1d，ψ1q就尤为关键。

BSRM的转矩绕组磁链可通过电压模型估计方法估算出来。在两相旋转坐标系下，其模型：

(19)

式中：ed，eq为电机转矩绕组定子的反电动势；u1d，u1q为电机转矩绕组的等效电压；R1为电机转矩绕组的电阻。

式(19)中的纯积分环节会引起积分初始化偏差与直流偏置的问题，为解决此类问题，将式(19)中的纯积分环节以输入信号截止频率ωc的低通滤波器1/(s+ωc)来代替[6]。则改进的转子磁链如下：

(20)

式中：s为拉式算子。

将式(20)代入式(17)中，即可求得电机的转子径向位移量。则BSRM无位移传感控制框图如图3所示。图中的磁链观测器的内部结构由图4表示。

图3 BSRM无位移传感控制框图

图4 磁链观测器内部结构图

3 仿 真

在上述分析的基础上，基于MATLAB仿真环境，对BSRM的无位移传感进行了仿真。电机的相关参数如表1所示。

表1 BSRM参数

仿真采用变步长为ode23tb的仿真算法，仿真时长为0.5 s。转子初始位置坐标为(0.1 mm，-0.1 mm)，电机给定转速为3 000 r/min。

图5为电机的转速曲线。t=0时，电机空载起动，在t=0.13 s左右达到3 000 r/min，并匀速运行至仿真结束。由图5可知，在电机控制系统加入无位移传感器后，电机转速具有较快的动态响应性能，且波形无明显波动，表明基于电感矩阵模型的无位移传感技术对无轴承电机的正常运行无明显影响，因此该方法适用于BSRM。

图5 电机转速曲线

图6(a)、图6(b)分别为电机在同一仿真周期内，在α轴，β轴方向上实际转子位移量与估算转子位移量的对比图。由图6可知，转子能迅速到达平衡位置，实现稳定悬浮；两者之间的位移误差较小，且最大误差远远小于电机的平均单边气隙长度。因此，证明本文提出的基于电感矩阵模型的BSRM无位移传感自检测技术是可行有效的。

(a)α轴(b)β轴

图6 转子位移对比图

4 结 语

本文提出一种基于电感矩阵模型的BSRM无位移传感的方法以代替传统的电涡流传感器。理论分析与仿真实验结果均表明：该方法可在实现BSRM稳定悬浮的同时，能够有效检测出转子位移量信号，实现转子位移的跟踪估计。该方法简单易行，并降低了整个电机控制系统的成本，缩减了电机长度与体积，利于BSRM的进一步发展。因此，该方法具有潜在的研究价值与应用前景。

[1] 年珩，贺益康.感应型无轴承电机磁悬浮力解析模型及其反馈控制[J].中国电机工程学报，2003,23(11)：139-144.

[2] CHIBA A，FUKAO T，ICHIKAWA O,et al． Magnetic bearings and bearingless drives[M]． London：Newnes，2005：239-249．

[3] 张汉年.无轴承同步磁阻电机基础理论与实验研究[D].镇江：江苏大学，2006.

[4] 张伟霞.无轴承异步电机悬浮力模型与数控系统研究[D].镇江：江苏大学,2008.

[5] 朱熀秋，王成波，张伟霞.基于电感矩阵的无轴承电机径向悬浮力模型[J].江苏大学学报(自然科学版),2009，30(1)：53-57

[6] 王钧铭,鲍安平,张汉年,等.无轴承同步磁阻电机的转子位移观测策略[J].信息化研究，2013，39(5):9-12.

Self-Sensing of Rotor Radial Displacement for Bearingless Synchronous Reluctance Motor

XUEn-xiang,ZHUHuang-qiu

(Jiangsu University, Zhenjiang 212013,China)

In order to ensure the stable operation of bearingless synchronous reluctance motor (BSRM), it is necessary to control the rotor position. Then the relevant sensors (eddy current sensor) should be used to detect the eccentricity of the rotor displacement. To reduce the total cost of BSRM and decrease the length and volume of the motor, the rotor displacement sensor can be canceled. In this paper, a model based on the inductance matrix of BSRM was deduced. Then, a displacement self-detection method for BSRM was proposed. Through the establishment and analysis of the accurate model, the rotor displacement observer was designed. And based on MATLAB/Simulink software, the BSRM control system was built to verify the proposed theory. Simulation results demonstrate that this method can effectively predict the eccentricity of the rotor accurately.

bearingless synchronous reluctance motor (BSRM); inductance matrix; displacement sensorless; self-sensing

2016-01-19

江苏省高校科研成果产业化推进工程项目(JHB2012-39)；江苏省“青蓝工程”项目(2014)；江苏省“333工程”项目

TM352

A

1004-7018(2016)05-0014-03