基于通勤行为的电动汽车充电站选址模型*
2016-05-25潘晓锋
左 志 王 涛 潘晓锋 刘 锴
(大连理工大学交通运输学院 大连 116024)
基于通勤行为的电动汽车充电站选址模型*
左志王涛潘晓锋刘锴
(大连理工大学交通运输学院大连116024)
摘要:提出一种基于通勤行为的电动汽车充电站选址模型,该模型考虑了电动汽车初始电量的分布和出行者的里程焦虑程度.同时还给出了模型求解算法,并通过算例路网验证了模型的有效性.研究结果表明,由模型求得充电站设置节点较为集中,即该模型有较强的稳定性;基于往返出行链的电动汽车充电站选址模型虽然会增大路网总出行时间,但是可以有效避免返程出行失败的情况;出行者的里程焦虑程度对充电站选址影响较大,且对路网总出行时间存在明显的影响.
关键词:城市交通;充电站选址模型;通勤行为;电动汽车;里程焦虑
0引言
近年来,小汽车尾气排放受到越来越多的关注.随着小汽车保有量的不断上升,节能减排的呼声日益高涨.电动汽车作为一种污染小、效率高的替代方案进入了人们的视野.一般而言,电动汽车可以分为三类:纯电动汽车、混合动力汽车,以及燃料电池汽车.有研究者认为,完全依靠电力的纯电动汽车将是私人交通电气化的最终方案[1].目前,电动汽车受到行驶里程及有限的充电设施的限制而难以大范围推广.因此,合理进行充电站选址成为当前研究的热点问题.
国外对于充电站选址问题做了大量的研究.He等[2]考虑城市电网与道路网络的耦合,提出了基于该耦合网络的充电站选址模型,该模型的研究对象为插电式混合动力电动汽车,因而没有考虑出行者使用纯电动汽车时的一个重要心理因素——里程焦虑.Lee等[3]考虑到电动汽车电量的分布,建立了充电站选址双层模型,上层为系统最优模型,下层为用户均衡模型.然而该模型假设电动汽车电量服从均匀分布,且没有对出行失败(因为电池电量不足而无法到达目的地)的出行者做出解释与说明.
国内对于充电站选址问题也有相关研究.周洪超等[4]提出运用博弈论对电动汽车充电站备选方案进行评价,从而确定最终规划布局.孙小慧等[5]建立了满足等待时间最短和服务最便利的时空优化布局动态模型.纵观国内研究,以不同布局方案之间的对比评价居多,而考虑电动汽车的交通特性、出行者的选择行为特性的研究较少.
鉴于现有研究的不足,本文提出一种基于居民通勤行为的电动汽车充电站选址双层模型.该模型以纯电动汽车(以下简称为电动汽车)为研究对象.此外,本文还将里程焦虑以里程余量的形式引入充电站选址模型之中,以探究里程焦虑对充电站选址和优化目标函数路网总出行时间的影响.
1基于居民通勤行为的充电站选址模型
1.1出行者路径选择规则
本文主要考虑城市内部的通勤出行.假定家庭居住地有完善的充电设施,公共场所为充电设施待建区,而工作场所无充电设施(工作场所由于空间限制以及费用因素一般未设置充电设施;此外,工作场所即使拥有充电设施,也是提供给内部人员使用,不宜视为公共充电站.因此本文假定工作场所没有充电设施).把驾驶电动汽车的出行者从家到单位的上班出行和从单位返回家的下班出行组成一条出行链,见图1.
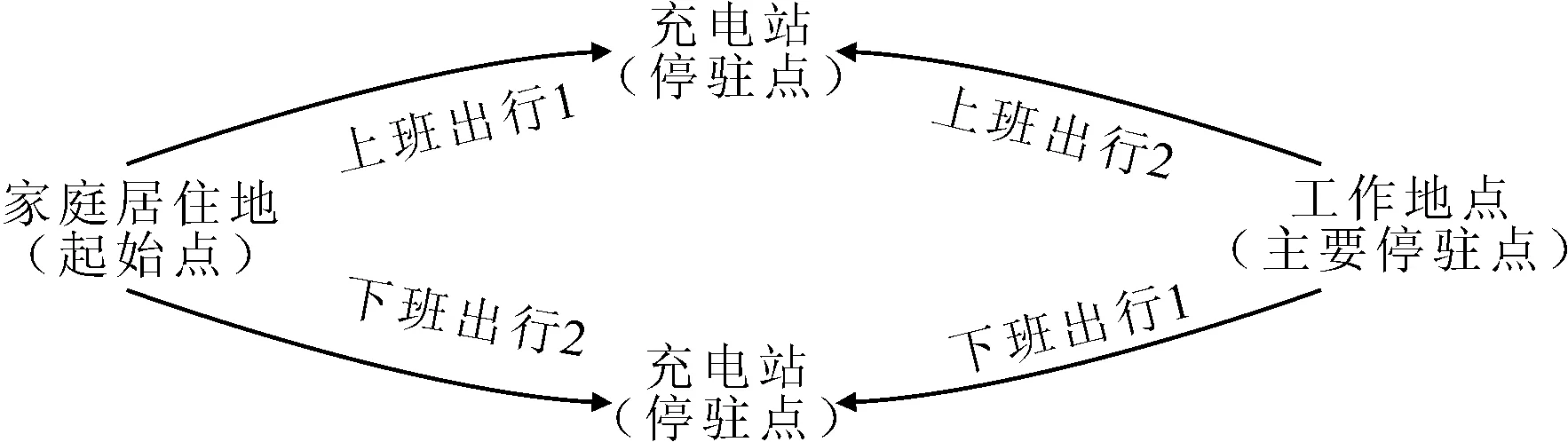
图1 出行者往返出行链示意图
出行者在上班出发之前,将面临出行路径的选择.这里将根据出行者的充电行为对通勤路径进行分类.在进行分类之前作如下假设:(1) 假设电动汽车的行驶里程限制值大于所有OD的起终点距离,即保证在整个通勤出行中,至多在往返途中各进行一次充电行为;(2) 假设出发时刻电动汽车的初始电量满足某一概率分布;(3) 假设出行者对路网信息有充分了解,这为其选择最优路径提供依据.
基于上述假定,出行者根据电动汽车初始电量进行路径选择:首先,需要进行充电与否的判断,以能否完成上班出行并且下班返程中到达距工作地点距离最短的充电站为判断标准,此为一级选择;其次,在确认需要充电的前提下,选择合适的充电站.选择充电站的依据是在电动汽车能到达的充电站集合中,选取路径行程时间与充满电池所需时间之和最小的路径.此外,特别假设,对于部分车辆无法到达充电站的情况,视其为在家中提前充满电池(这也是符合现实情况的).在下班返程前,出行者要进行相似的选择过程,不同点在于:一级选择中,由于家庭居住地有充电设施,判断标准变为电动汽车是否能完成下班出行;第二级选择中,返程中不会出现车辆无法到达充电站的情况,这也是基于往返出行链模型相较于基于单程出行模型在研究充电站选址问题的优点.具体的选择过程见图2及表1.

图2 基于往返出行链的路径选择方案示意图

序号出行类别判断结果选择路径a上班需要充电,但无法到达最近充电站2b上班需要充电,可以达到充电站1c上班不需要充电2d下班需要充电,可以达到充电站4e下班不需要充电3
里程焦虑是伴随电动汽车产生而出现的.出行者在判断电动汽车需要进行充电时,出于对电动汽车完成出行任务不确定性的担忧,会保留一定的电池余量作为安全储备值.里程余量的大小能够反映出行者的里程焦虑的程度,其值越大,出行者焦虑程度越高,反之亦然.鉴于此,本文采用里程余量表征出行者的里程焦虑程度,见表3.
1.2模型建立
基于电动汽车出行者路径选择规则,本文提出了基于居民通勤出行的充电站选址双层优化模型.上层模型是一个系统最优模型,以路网总出行时间为优化目标;下层模型是基于出行者路径选择规则的用户均衡模型.上层模型确定各OD对间交通量选择各个充电站充电的出行比率,无需充电的出行比率,无法到达充电站的出行比率等变量,这些变量在下层模型中作为已知量,进行各路段流量的分配.模型中还考虑里程余量以及初始电量分布.
上层模型:
min∑xata(xa)
(1)
约束条件:
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
下层模型:
(11)
约束条件:
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
(20)

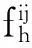
ta0为路段a的自由流通行时间;Capa为路段a的通行能力;α,β为BPR函数的系数,一般α=0.15,β=4.
式(1)~(10)为上层模型,式(1)为系统最优的目标函数;式(2)指出充电站的设置个数;式(3)、(4)保证往程与返程中,需要充电的出行者选择的充电地点设置了充电站;式(5)、式(6)保证出行者在OD对(i,j)间的备选充电站集合中选择使出行时间最短的充电站;式(7)~(9)确定往程出行各OD对间交通量选择各个充电站充电的出行比率,无需充电的出行比率,无法到达充电站的出行比率;式(10)确定返程出行各OD对间交通量选择各个充电站充电的出行比率与无需充电的出行比率之间的关系;式(11)~(20)为下层模型,式(11)为目标函数;式(12)为路网路段阻抗函数;式(13)、式(14)为不在出行途中充电的这部分OD交通流量;式(15)、式(17)为往程出行在出行途中充电的这部分OD交通流量;式(16)、式(18)为返程出行在出行途中充电的这部分OD交通流量;式(19)表示往返的交通流量相等;式(20)为路段交通流量.
1.3模型算法
为了求解该双层模型,本文算法包含出行者的路径选择规则、里程余量变化及不同充电站的组合.下层模型是用户均衡模型,为了简化模型算法,本文采用增量分配法进行流量分配.在UE规划的算法提出之前,增量分配法被大量使用,而且至今仍被广泛运用[6].
2实例分析
2.1问题描述
SiouxFalls路网共24个节点,76个路段(见图3).本文选择(1,20),(2,13)两组OD对,每对OD的交通需求均为1 000veh/h.其中,节点1,2为家庭居住地,有完善的充电设施;节点13,20为工作单位,无充电设施;余下20个节点为公共场所,为充电设施待建区.在实例中,假设路网共设置4个充电站.路网特性见表2,电动汽车的特性数据见表3.
3.2结果及分析
通过模型算法计算,首先得到不同里程余量下最优充电站分布节点的位置及对应的路网总出行时间.对于电动汽车的出行者群体而言,出行者个体的里程焦虑程度各异,所以倾向的里程余量值不同.据此,本文统计得到不同里程余量下最优充电站节点出现的频数(见表4),取频数位居前4位的节点作为最终充电站的位置,见图3.从统计结果看,不同里程余量对应的充电站最优位置较集中,说明该模型稳定性较好.

图3 充电站位置示意图
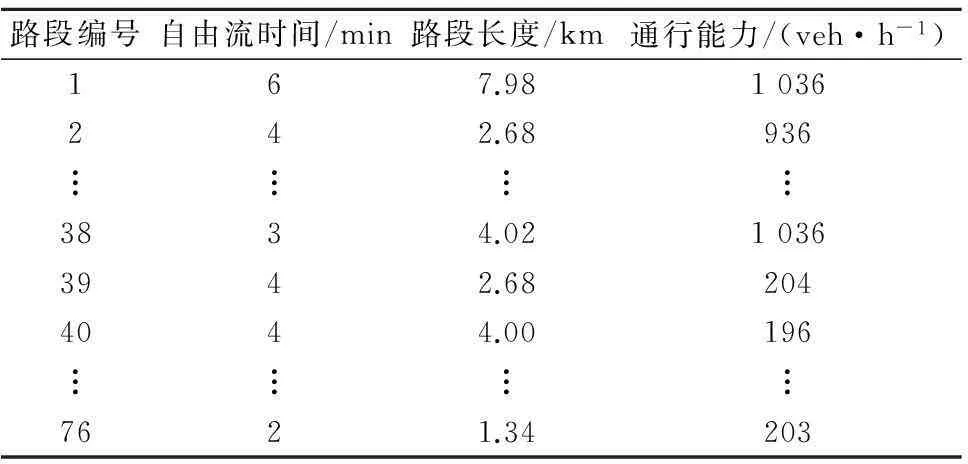
路段编号自由流时间/min路段长度/km通行能力/(veh·h-1)167.981036242.68936︙︙︙︙3834.0210363942.682044044.00196︙︙︙︙7621.34203

表3 电动汽车特性表

表4 节点出现频数统计表
考虑到现阶段大多数工作单位缺少充电设施,模型基于通勤出行链建立.基于通勤出行链模型上班出行和下班出行连接起来,视为一个整体;而基于单程出行模型仅考虑上班单向出行.下文将基于通勤出行链模型称模型I,而把基于往程出行模型称模型II(模型II与模型I的不同之处有如下两点:(1)模型II考虑的出行过程是上班单程出行;(2)在出行者进行路径选择过程中,判断标准是电动汽车能否到达上班地点完成上班出行,而不用到达返程中最近充电站).通过比较模型I和模型II的运算结果,说明基于通勤出行链模型充电设施选址的必要性和优越性.
图4显示了模型II的电动汽车返程时不同里程余量对应的出行失败交通量.从图可得,不同里程余量下返程出行失败车辆数最小值达到70 veh/h,而最大值将近400 veh/h,占到总出行需求的10%~40%.模型I视往返出行作为整体,在往程出发时刻就保证车辆返程能够到达最近充电站,所以不会出现返程出行失败.

图4 模型Ⅱ中返程失败交通量与里程余量系数关系图
图5显示了应用2种模型计算得到往程出行的路网总出行时间最小值与里程余量关系图,两者在同一目标函数下的优化结果不同.从图可得,当里程余量从1%变化到30%时,模型I的最优结果均大于模型II的最优结果.对比两模型原理的差异,模型I在往程出发时刻判断电动汽车充电的条件是其初始电量在一定里程焦虑水平下保证返程出行能够顺利进行,而模型II则只是考虑是否能够到达工作地点.因此,在模型I中,会有更多车辆由于需要充电而产生了绕行,从而增加了路网总出行时间.
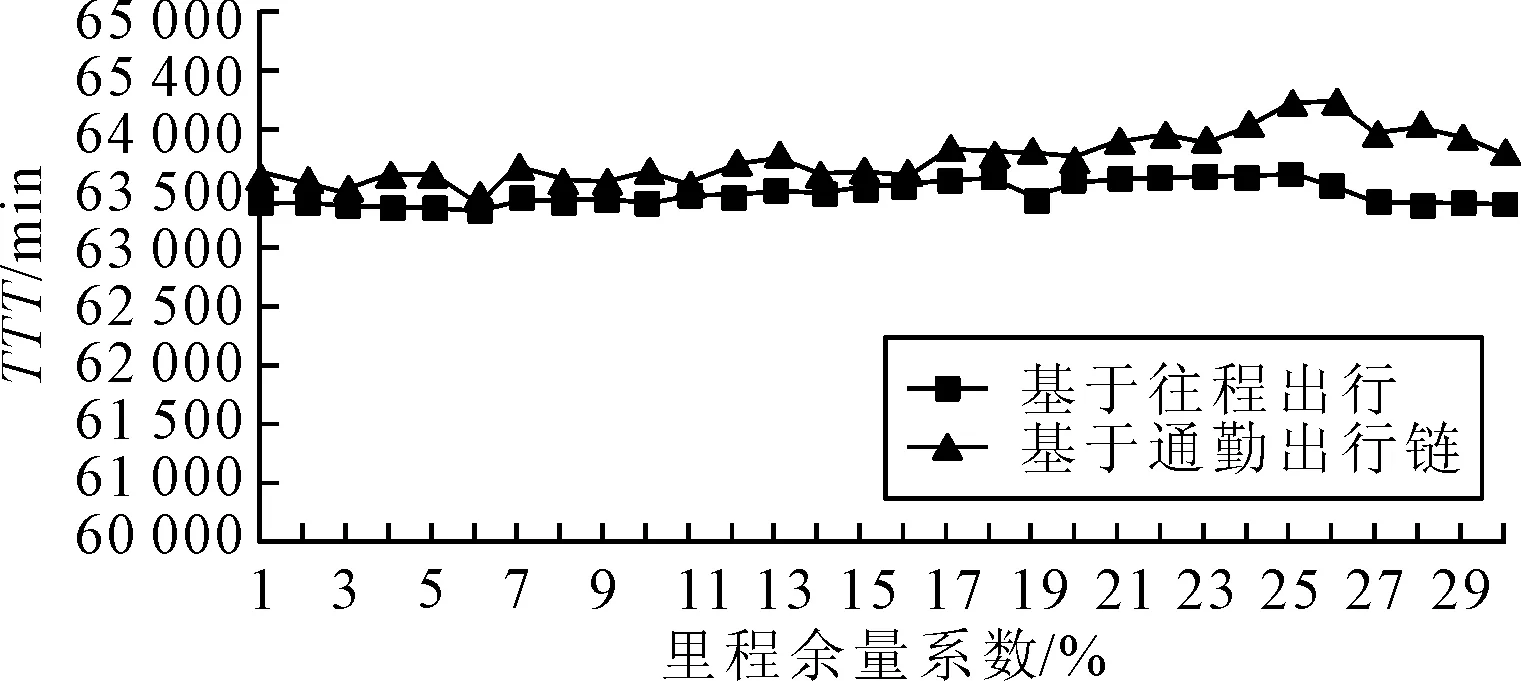
图5 路网总出行时间与里程余量系数关系图
从上述可得,模型I和模型II相比,其优点是将上班出行与下班出行看作一条出行链,保证不会出现返程出行失败的情况;而缺点是所求得的路网的往程总出行时间较大.里程焦虑是影响电动汽车广泛使用的主要障碍之一,而出行失败状况的出现,将会增加出行者的里程焦虑程度,这是充电站选址时应该避免的情况.此外,由于本文提出的双层模型的下层问题为用户均衡规划,因此不会由于较多的充电绕行而导致路网局部交通状况恶化,且从图5中看出,两者的最大差值不超过1%.所以可以认为基于往返出行链的电动汽车充电站选址模型更为合理.
图6显示了应用模型Ⅰ时路网的往返全程总出行时间与里程余量关系.从图中可以看出:总出行时间与里程余量系数呈线性关系,其中拟合度R2=0.554 6,说明总出行时间与里程余量系数线性关系显著.
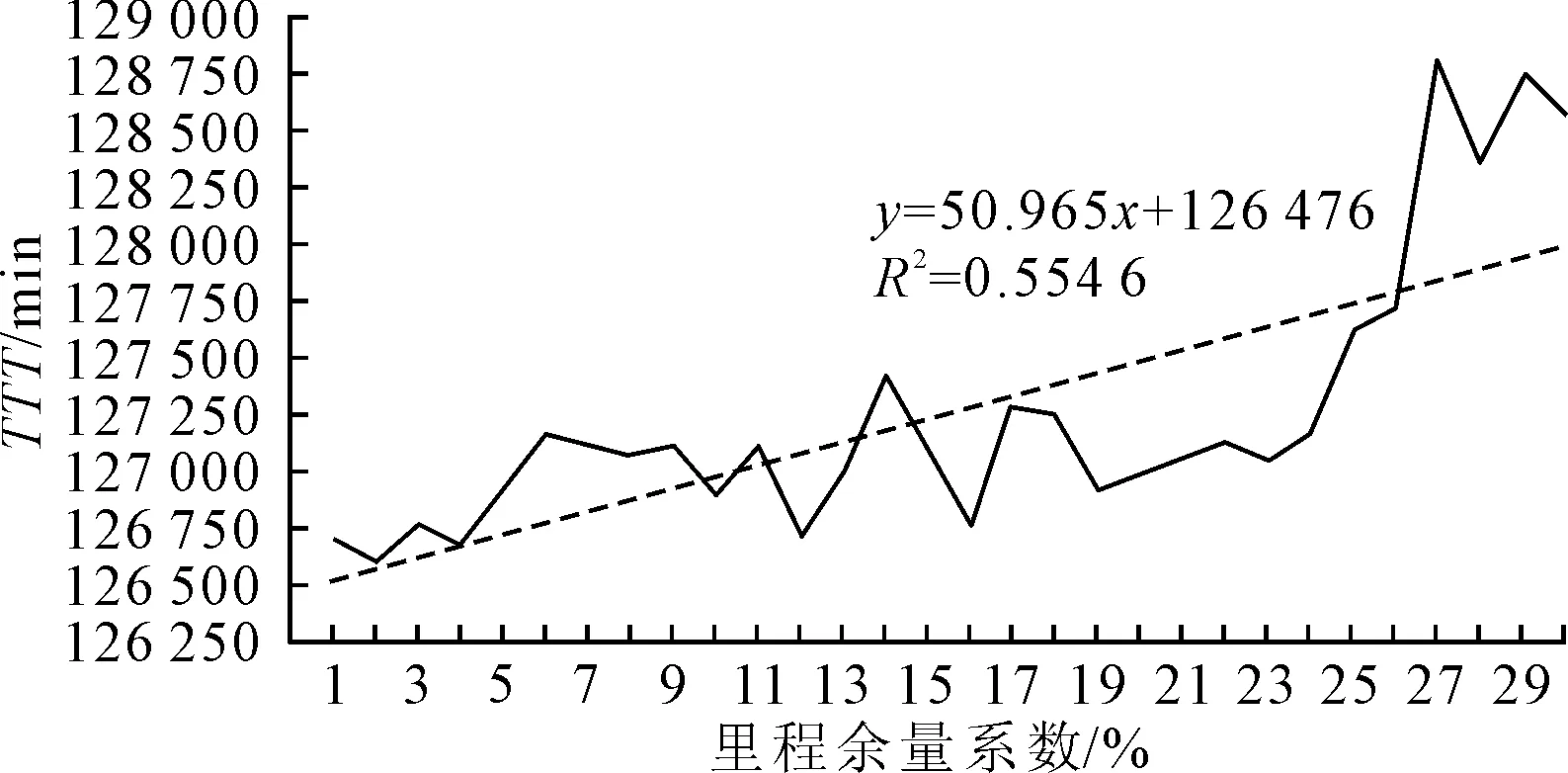
图6 往返总出行时间与里程余量系数关系图
4结论
1) 就统计结果而言,不同里程余量对应的充电站设置节点较为集中,说明该模型求解的稳定性较好;
2) 本文提出的模型能够避免返程出行失败的情况,同时也因此而增加了出行者的绕行,导致了路网总出行时间的增加;
3) 总出行时间与里程余量呈线性关系,其中拟合度R2=0.554 6,说明总出行时间与里程余量系数线性关系显著.
参 考 文 献
[1]LIN Z, GREENE D L. Promoting the market for plug-in hybrid and battery electric vehicles[J]. Transportation Research Record: Journal of the Transportation Research Board, 2011, 2252(1): 49-56.
[2]HE F, WU D, YIN Y, et al. Optimal deployment of public charging stations for plug-in hybrid electric vehicles[J]. Transportation Research Part B: Methodological, 2013, 47: 87-101.
[3]LEE Y G, KIM H S, KHO S Y, et al. UE-based location model of rapid charging stations for evs with batteries that have different states-of-charge [C]. Transportation Research Board 93rd Annual Meeting,2014:809-814.
[4]周洪超,李海峰.基于博弈论的电动汽车充电站选址优化模型研究[J].科技和产业,2011,11(2):51-54.
[5]孙小慧,刘锴,左志.考虑时空间限制的电动汽车充电站布局模型[J].地理科学进展,2012,31(6):686-692.
[6]栾琨,隽志才,宗芳.通勤者出行方式与出行链选择行为研究[J].公路交通科技,2010,27(6):107-111.
Location Model for Electric Vehicle Charging Stations Based on Commuting Behavior
ZUO ZhiWANG TaoPAN XiaofengLIU Kai
(SchoolofTransportation&Logistics,DalianUniversityofTechnology,Dalian116024,China)
Abstract:An Electric Vehicle (EV) charging station location model based on commuting behavior is presented in this study, considering both the distribution of the remaining fuel range of EVs and travelers' degree of range anxiety. Solution algorithm is also given and model validation is conducted through a numerical road network. Result shows that the calculated setting nodes of charging stations are relatively concentrated, that is, the model has a virtue of strong stability. The model can effectively avoid the failure of return trip case in spite of increasing the network total travel time. Travelers' range anxiety degree has significant effects on charging station location and the network total travel time.
Key words:urban traffic; charging stations location model; commuting behavior; Electric Vehicle (EV); range anxiety
doi:10.3963/j.issn.2095-3844.2016.02.007
中图法分类号:U491.1
收稿日期:2016-02-14
左志(1980- ):男,博士,讲师,主要研究领域为交通需求管理
*国家自然科学基金项目(51278087,51378091)、辽宁省教育厅科学研究一般项目(L2012026)资助
