一种高效的电力变压器绕组轴向固有振动频率计算模型

李凯琪， 郭 健， 刘 军， 张安红， 俞少佳

(1. 南京航空航天大学， 江苏 南京 211106； 2. 钱江电气集团股份有限公司， 浙江 杭州 311243)

一种高效的电力变压器绕组轴向固有振动频率计算模型

李凯琪1， 郭 健1， 刘 军2， 张安红2， 俞少佳2

(1. 南京航空航天大学， 江苏 南京 211106； 2. 钱江电气集团股份有限公司， 浙江 杭州 311243)

在电力变压器设计过程中，绕组的固有振动频率是一个非常重要的性能参数。本文基于弹性动力学理论，根据绕组周向垫块弹性支撑等效原则，提出了一种高效的计算电力变压器绕组轴向固有振动频率的二维有限元模型，其固有振动频率的计算具有与三维模型一致的结果，但其计算效率得到大大的提高。同时研究表明，增加垫块的宽度和数量，以及增大预紧力都可以提高绕组轴向的固有振动频率，是避免绕组共振的一种有效应对方法。最后通过对固有振动频率计算的实例校核，验证了本文所提二维模型方法的有效性。

电力变压器； 绕组； 高效有限元模型； 轴向固有振动频率

1 引言

在电力变压器设计过程中，绕组的固有振动频率是一个非常重要的性能参数[1]，当固有振动频率与电动力的频率相接近时，将产生谐振现象[2]。这种振动可能会导致比预紧力大得多的动态力，从而使油道垫块与线饼之间分开，进而引起绕组的松散、扭转，甚至倒塌，最终使得变压器绕组失稳而无法正常运行[3,4]。对于大型电力变压器，由于绕组辐向固有振动频率要远远大于其运行过程中承受的电动力频率，故而辐向固有振动频率在变压器设计过程中一般不考虑。而绕组轴向由于采用导线-垫块-导线的结构形式，其轴向固有振动频率值大大降低，结构设计稍不合理，就会导致线圈发生共振，这也成为变压器轴向失稳或运行噪音过大的一部分原因。因此，准确计算变压器绕组的固有振动频率，并通过改善结构形式使其避开轴向动态短路力的频率对于变压器设计和安全可靠运行具有重要的意义。

目前，变压器轴向固有振动频率的计算主要是基于“质量-弹簧-阻尼”的集中参数法和有限元法，由于有限元模型可以很好地兼顾绕组结构形式、支撑件结构力学特性等因素，相对于传统的集中参数法可以得到更加接近实际的计算结果。文献[5]建立了电力变压器固有振动频率计算的三维有限元模型，在轴向固有振动频率计算上取得了很好的效果；文献[6]在此基础上研究了轴向预紧力对固有振动频率的影响规律，并提出了改善变压器轴向稳定性的措施。综上，三维有限元模型在变压器轴向固有振动频率计算上具有较好的结果，但由于这种方法建模过程复杂，计算代价高，从而限制了该方法在工程实际中的普遍应用。

本文基于弹性动力学理论[7]，根据绕组周向垫块弹性支撑等效原则，提出了一种高效的计算电力变压器绕组轴向固有振动频率的二维有限元模型，其固有振动频率的计算结果具有与三维模型一致的效果，同时相对于三维模型，其计算效率亦得到大大的提高。最后，通过对固有振动频率计算的实例校核，验证了本文所提二维模型方法的有效性。

2 二维有限元模型

2.1 模型的提出

大型电力变压器的三维轴对称模型如图1所示。其中绕组的线饼是由绝缘垫块隔开的线段组成的，并被压紧在夹件之间；绕组中的垫块在相邻两饼铜线中起到一个支撑的作用，是变压器机械系统可靠性的一个重要的影响因素，在固有振动频率计算模型中必须予以考虑。为了能够兼顾到垫块沿绕组周向布置的特点，计算模型应属于三维问题，但是这将会使得固有振动频率计算的代价大大提高。

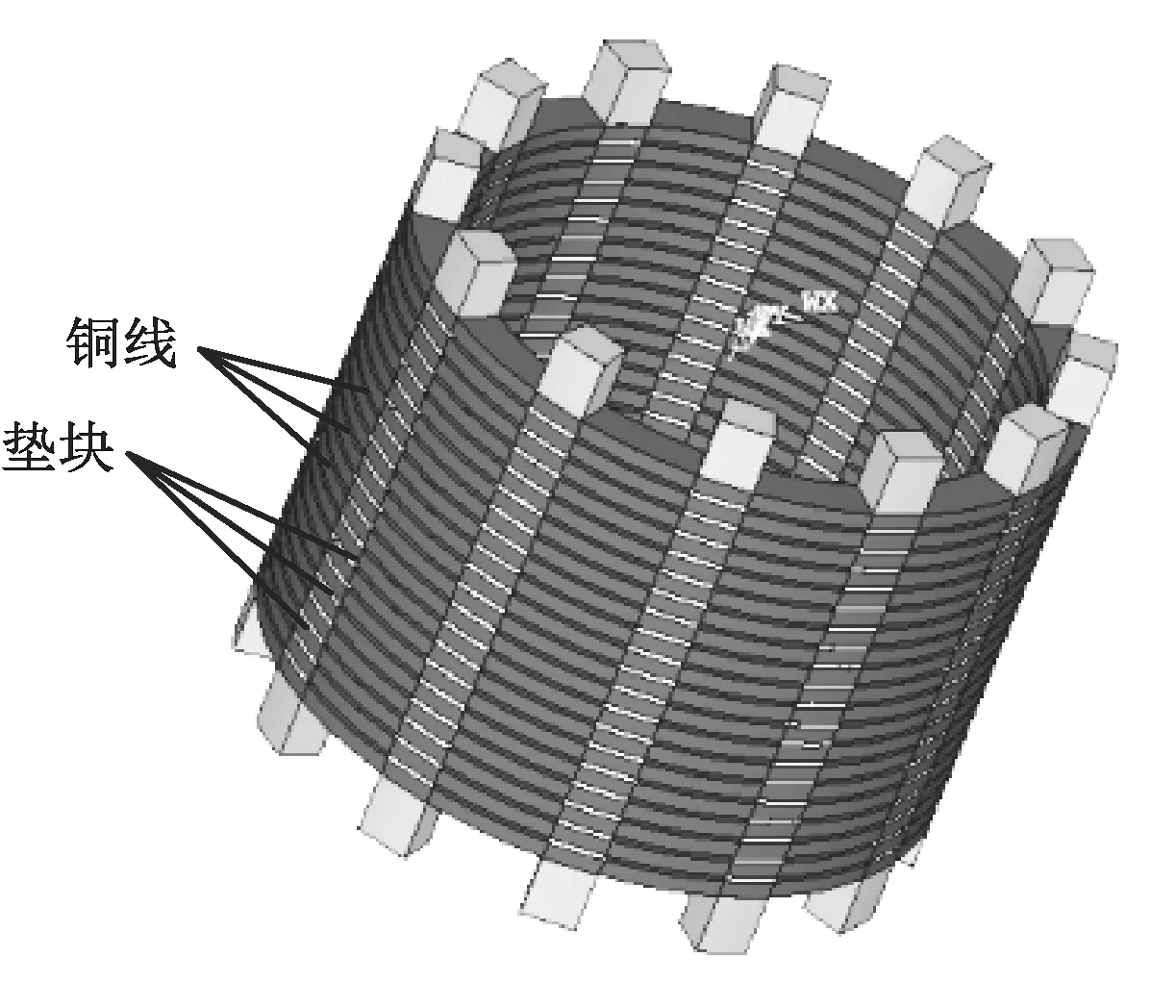
图1 三维轴对称模型Fig.1 3D axisymmetric model of winding

绝缘垫块受到导线轴向电动力压缩时，其受到的应力满足：

(1)

式中，δ为垫块受到的应力；F为垫块受到的轴向压力；∑A为两线饼间的垫块与线饼接触的实际面积之和。

根据胡克定理，垫块的应力-应变满足：

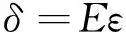
(2)

式中，ε为垫块的应变；E为垫块材料的弹性模量。

绝缘垫块由于受压导致线饼在轴向发生ΔZ的位移，位移与压力之间满足式(3)：

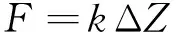
(3)

式中，k为垫块的等效弹性系数，反映了垫块对线饼的支撑作用。

由于线饼位移与垫块的应变满足ΔZ∝ε，因此

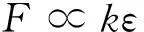
(4)

联立式(1)、式(2)和式(4)，则可以得到垫块的等效弹性系数与垫块材料的弹性模量，及垫块与线饼接触面积之间的关系：

(5)

由式(5)可以看出，只要E∑A为常数，则可以保证垫块对线饼的支撑效果不变。由此就可以将固有振动频率计算的三维问题简化为二维模型进行处理。

图2(a)为满足轴对称的三维计算模型，在该计算模型中绝缘垫块与线饼之间满足全接触，进一步可以得到简化的二维计算模型，如图2(b)所示。为了保证垫块对线饼的支撑效果不变，根据式(5)，垫块材料的等效弹性模量应满足：

(6)

式中，Ee为等效弹性模量；r1、r2分别为线饼的内、外半径。

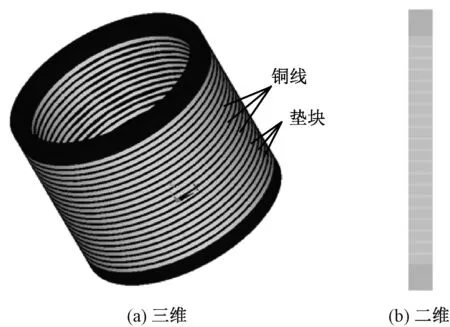
图2 绕组轴对称模型Fig.2 Axisymmetric models of winding

为了考虑轴对称处理后垫块质量对轴向固有振动频率的影响，还需要对垫块的密度做等效处理，等效密度满足：

(7)

式中，ρe为等效密度；ρ为垫块材料的实际密度。

2.2 控制方程

假定绕组的线饼是由绝缘垫块隔开的线段组成的，并被压紧在夹件之间。在研究绕组中的动态过程中，可以把它视为由有弹性联系的实体(线段)所组成的机械系统[8]。

基于图2(b)提出的有限元模型，并根据弹性动力学理论，各单元运动方程为：

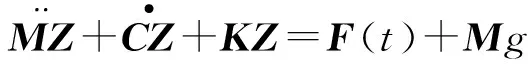
(8)

式中，Z为各线饼绝对位移；M为系统的质量矩阵；C为系统的阻尼系数矩阵；K为系统刚度系数矩阵；F(t)为垫块受到的轴向压力矩阵；g为重力加速度。

忽略阻尼的影响，且没有外力作用，可得绕组自由振动方程为：

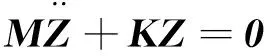
(9)

式(9)为线性齐次常微分方程组，其解可表示为：

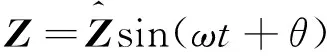
(10)

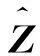
将式(10)代入式(9)，得：

(11)

该方程具有非零解的条件为：

(12)

解式(12)可得n个正实根ωi，则绕组轴向振动的固有振动频率为：

(13)

3 计算结果

3.1 二维模型计算结果

本文以文献[9]提出的模型为例，进行二维计算模型有效性的验证，模型对应的参数如表1所示。

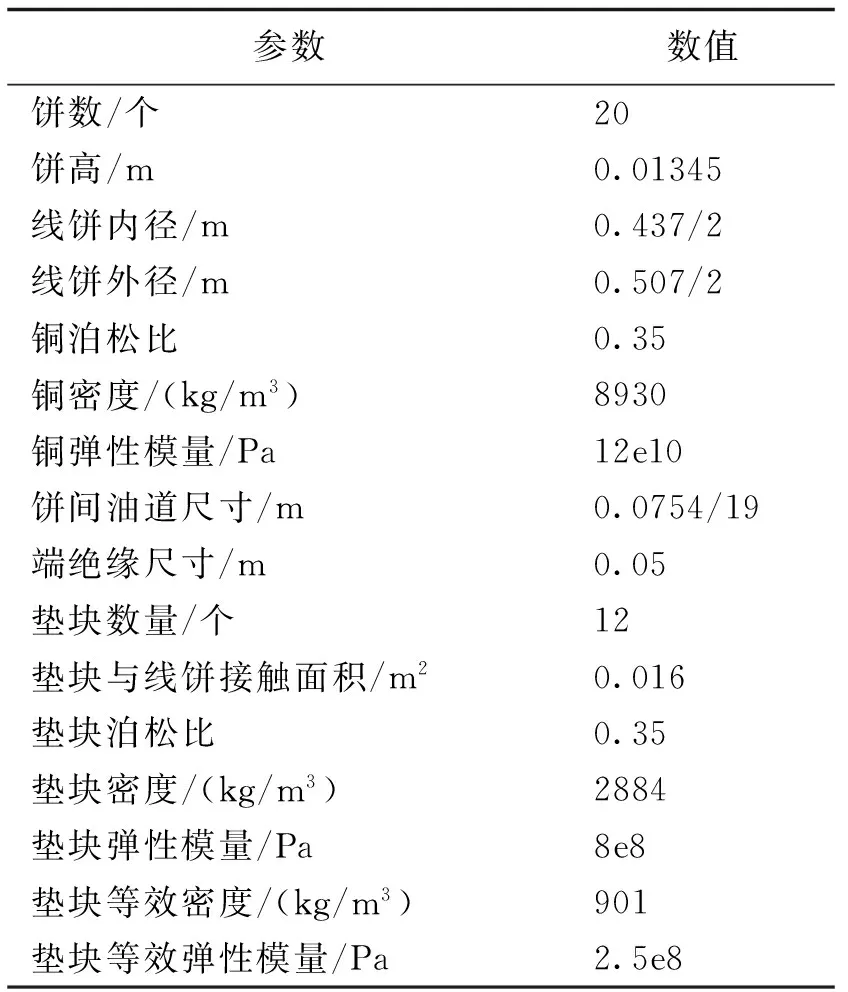
表1 模型参数

根据本文所提模型分析得到的固有振动频率及对应的振型如表2所示。

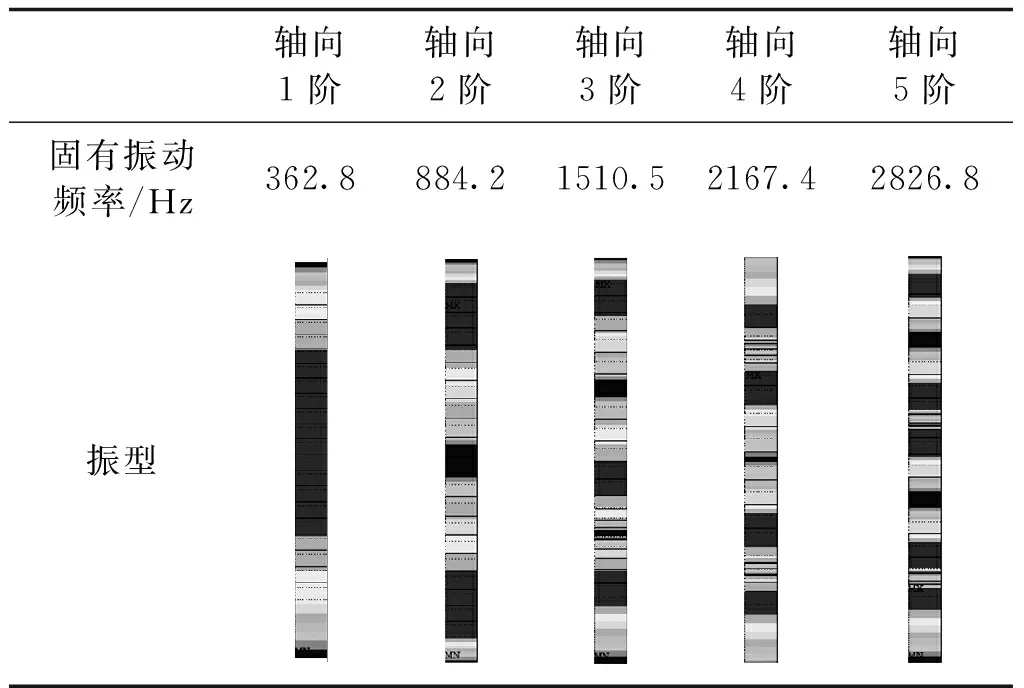
表2 固有振动频率对应振型

3.2 二维与三维计算比较

本文还将三维模型与二维模型的计算进行了比较。图3(a)为三维模型的网格划分图，图3(b)为三维模型得到的一阶轴向固有振动频率振型。

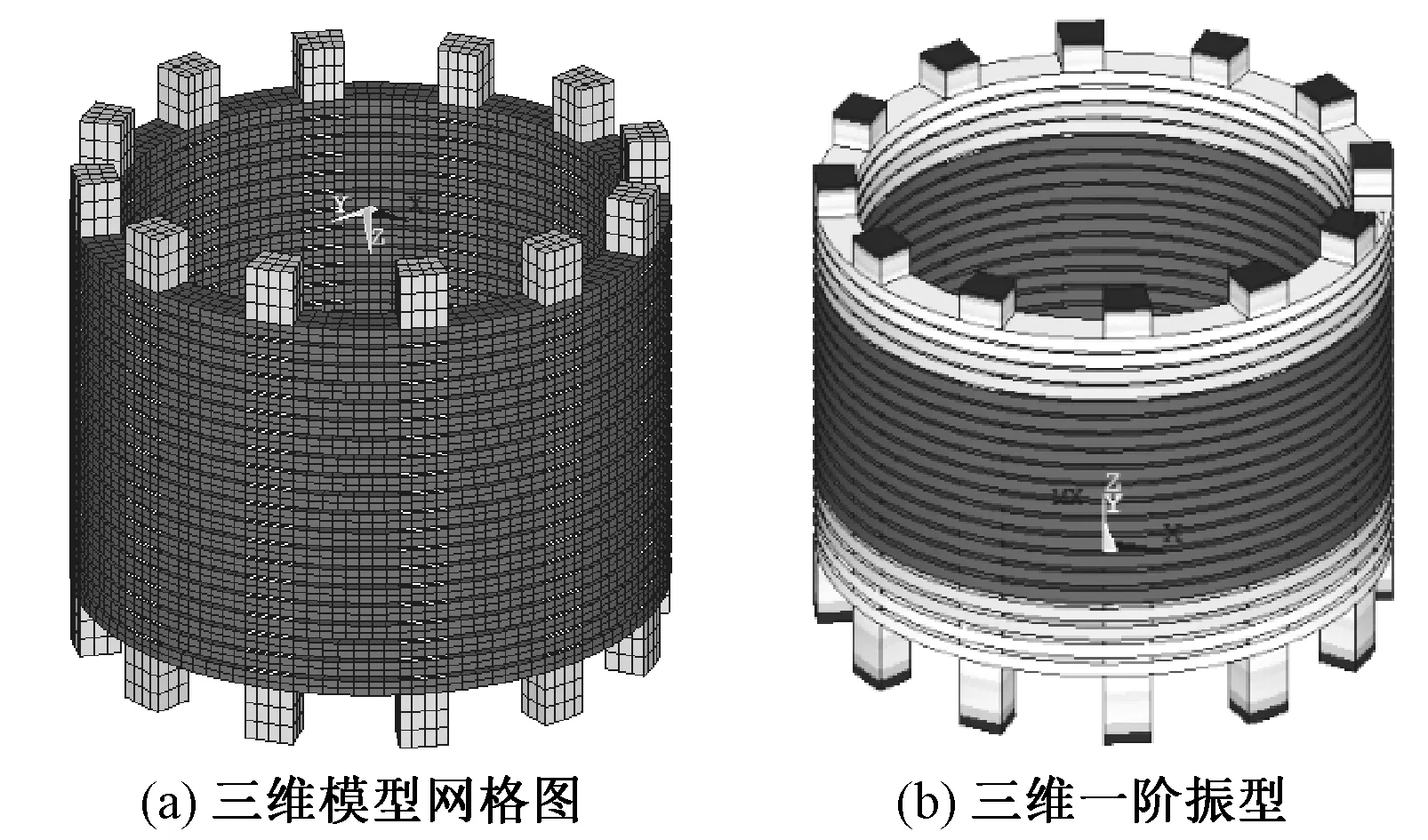
图3 固有振动频率对应振型Fig.3 Vibration models according to natural vibration frequency

表3列出了两种模型的计算结果与计算代价的比较。可以看出两种方法计算结果非常接近，但是在计算时间上，二维模型的计算效率要明显优于三维模型。

表3 固有振动频率结果比较

3.3 实验验证

对变压器模型的固有振动频率进行试验测试，表4列出了实验结果。可以看出，计算结果和实验所得结果基本吻合，证明了本文所提方法的有效性。

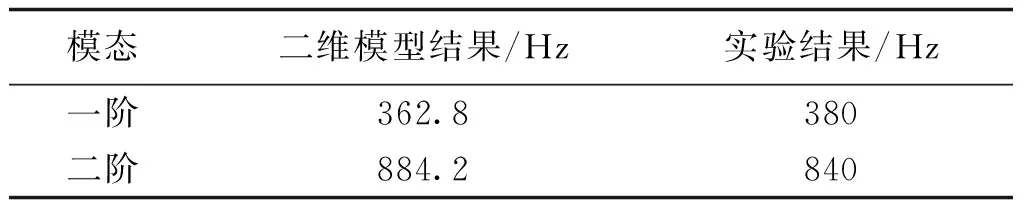
表4 二维模型结果和实验结果的比较

4 影响因素研究

由固有振动频率求解控制方程式(12)可知，固有振动频率的大小与机械系统等效的弹性系数及质量有关，系统质量的大小一般取决于变压器的电磁设计和经济成本，调整空间不大；而系统的弹性系数则取决于垫块对线饼的支撑，一方面，可以通过调整垫块的个数及尺寸来实现，另一方面，可以通过改变预紧力来实现对轴向固有频率的调整，是改善系统固有振动频率，避免共振的有效方法[10]。

本文以表1模型参数为例研究影响变压器绕组轴向固有振动频率的因素。表5列出了不同垫块的宽度对固有振动频率的影响；图4为对应的一阶固有振动频率关系曲线图。可以看出，随着垫块宽度的增加，垫块对线饼有效的支撑面增大，使得系统等效的弹性系数k增大，因此系统的固有振动频率亦成比例增大。

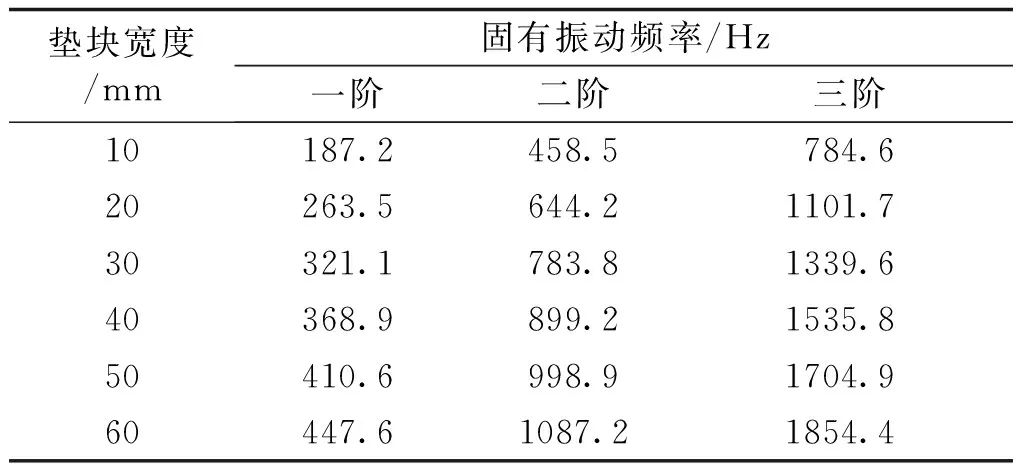
表5 变压器绕组不同宽度垫块时的固有振动频率

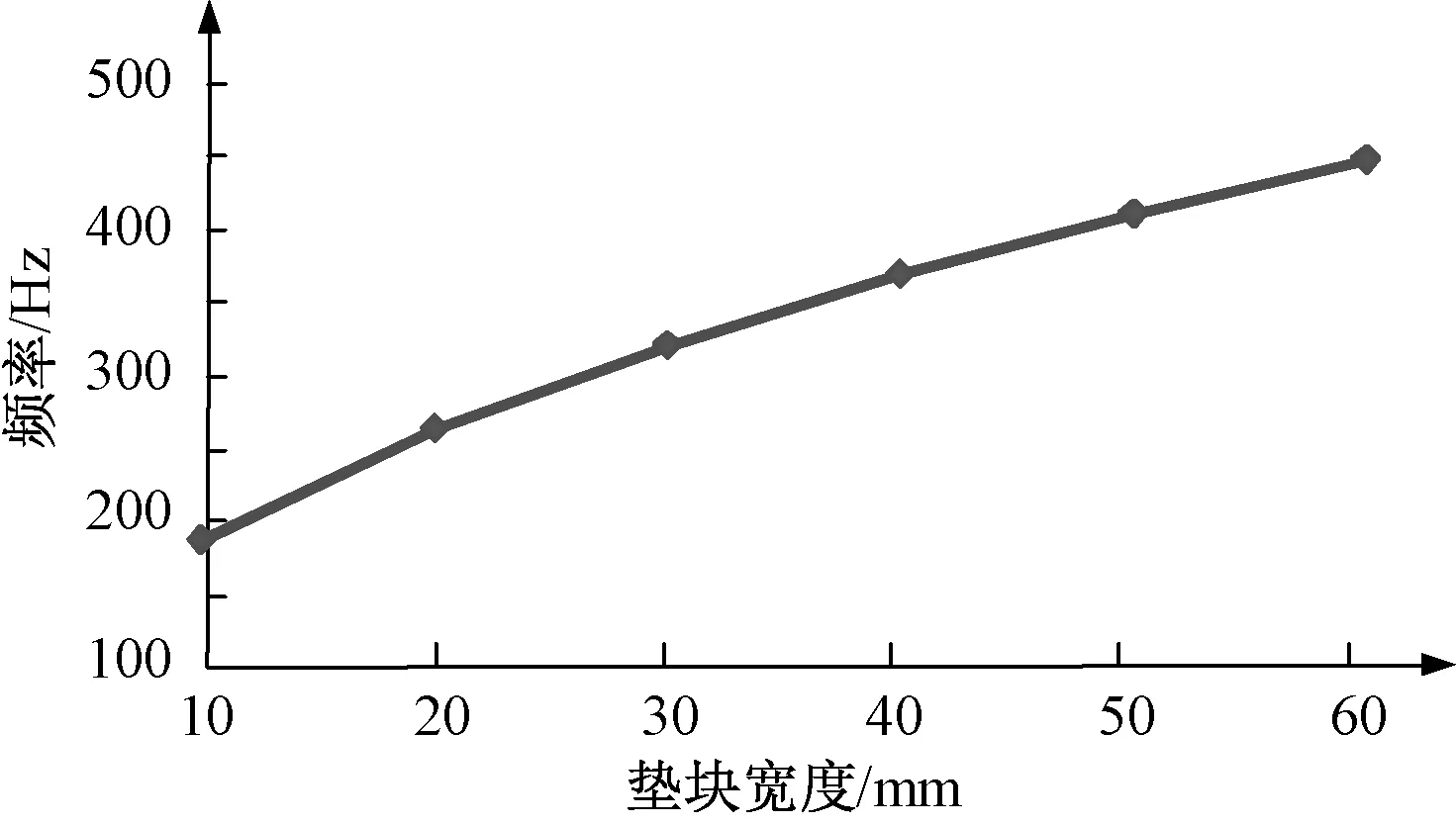
图4 垫块宽度-频率曲线Fig.4 Curve of pressboard’s width and frequency

表6列出了不同垫块的数量对固有振动频率的影响；图5为对应的一阶固有振动频率关系曲线图。可以看出，增加垫块的数量与增加垫块的宽度对固有振动频率具有相同的影响效果。

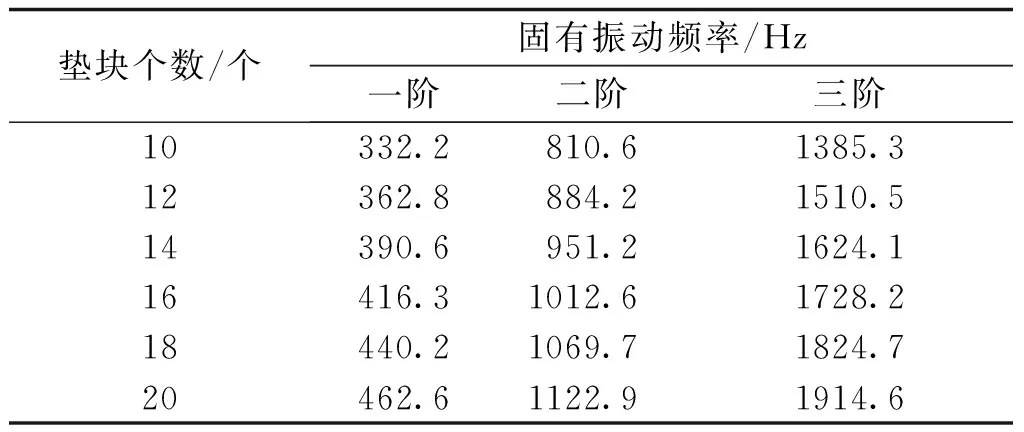
表6 变压器绕组不同个数垫块时的固有振动频率

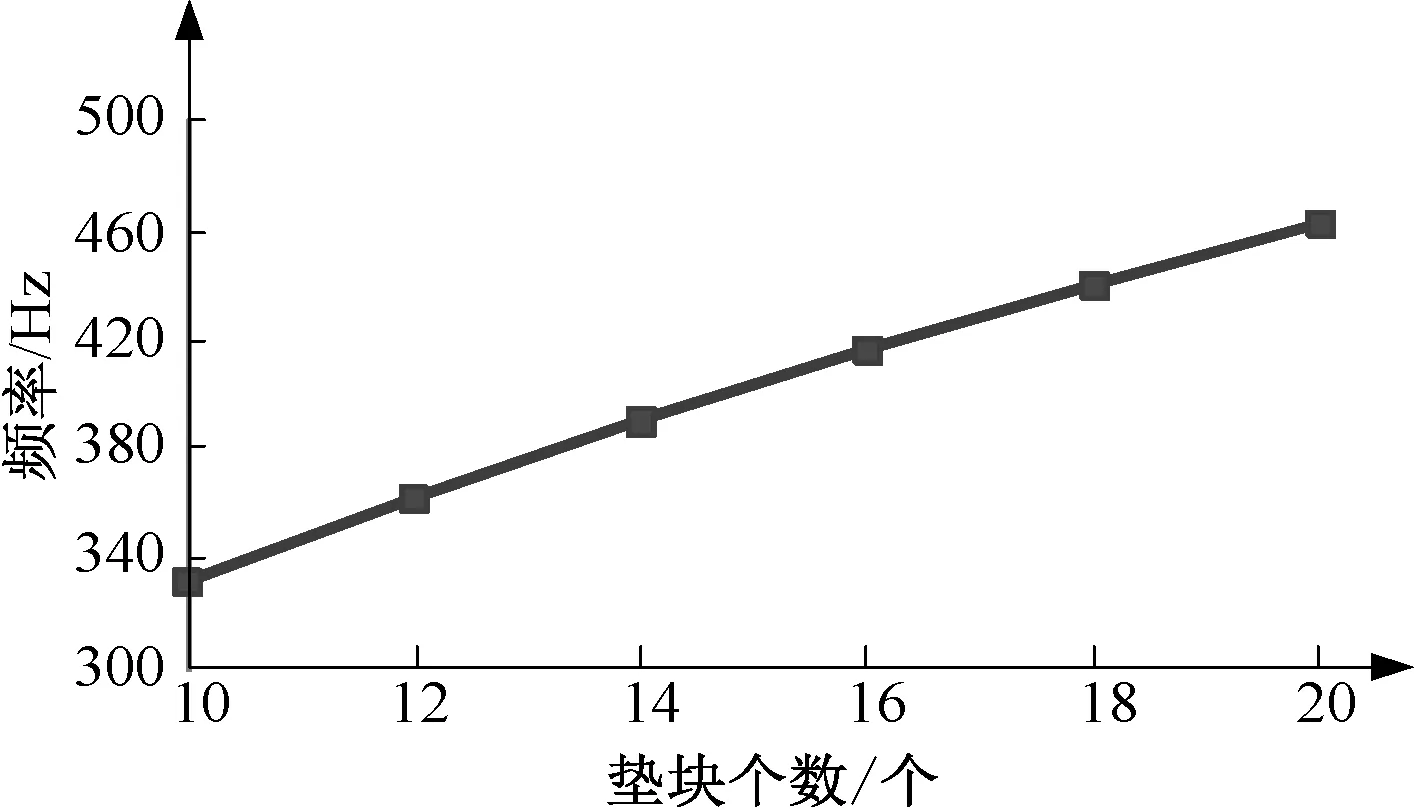
图5 垫块个数-频率曲线Fig.5 Curve of pressboard’s number and frequency

变压器绕组的绝缘主要是垫块及匝绝缘，其材料为绝缘纸板[11]。对于绝缘纸板，其静刚度为非线性，绝缘纸板在一定范围内(δ：0～103MPa)应力-应变关系可表示为：

(14)

式中，a为线性系数；b为硬化系数，可通过加载-变形试验测试得到[12,13]。a=1.05×102MPa，b=1.75×103MPa。

则弹性模量为：

(15)

假设施加在线圈上的预紧力为T，则

(16)

因此，可以通过改变等效的垫块的弹性模量来模拟预紧力的大小。

对应的等效刚度系数为：

(17)

式中，h为绝缘垫块的高度。

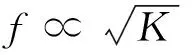
表7列出了变压器绕组在不同预紧力下的固有振动频率值。图6为对应的一阶固有振动频率关系曲线图。

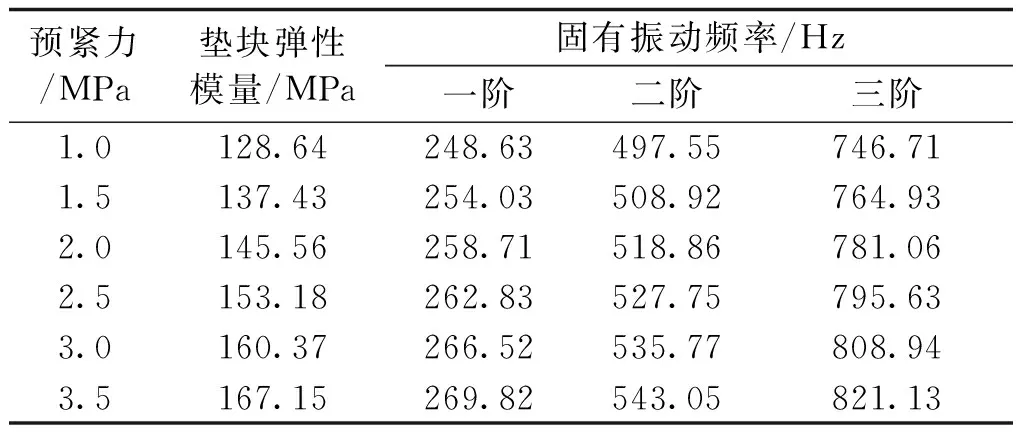
表7 变压器绕组不同预紧力下的固有振动频率

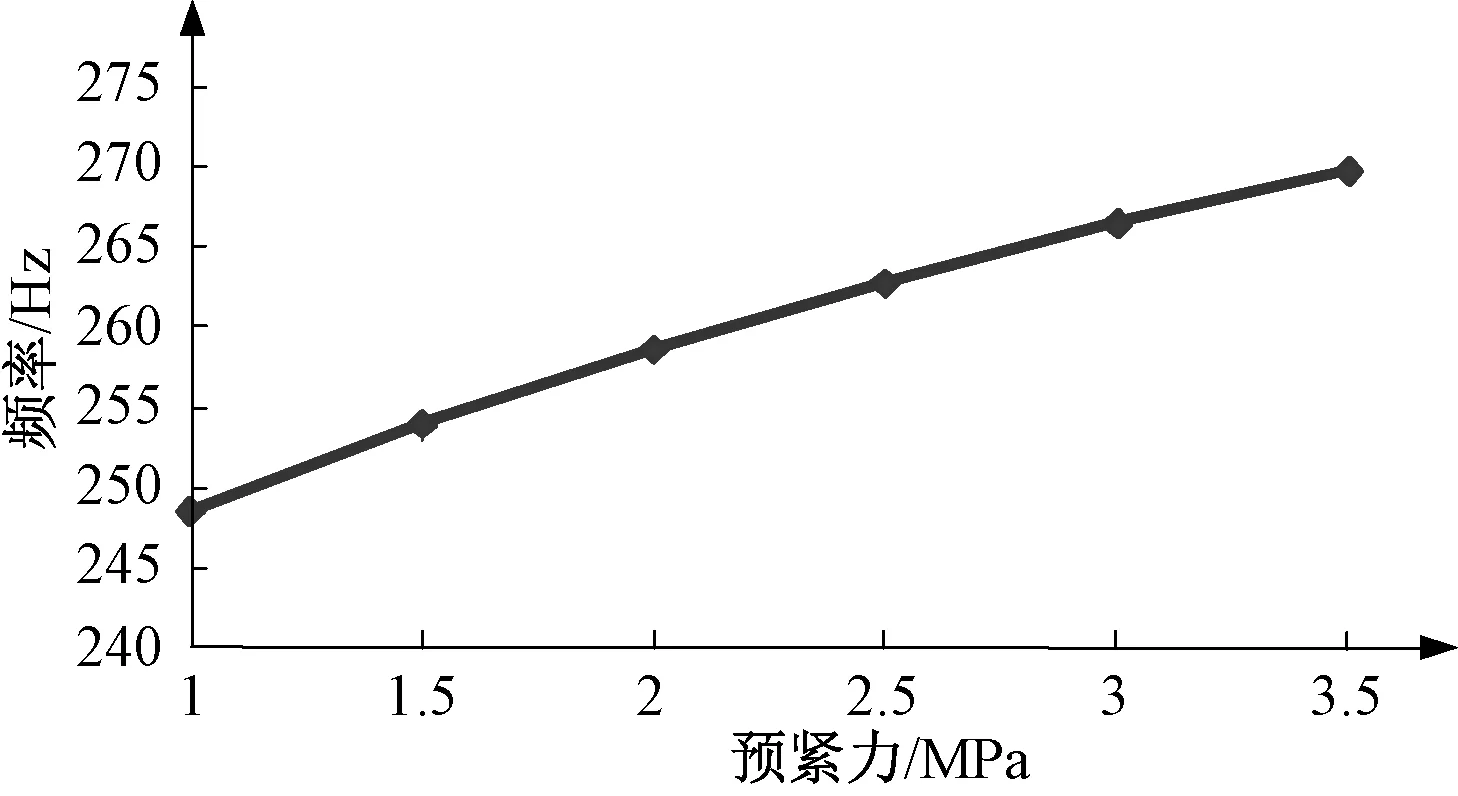
图6 预紧力-频率曲线Fig.6 Curve of pre-compression and frequency

可以看出，随着轴向预紧力的增大，绕组的各阶轴向振动固有频率都在提高，这是因为绕组的固有振动频率在很大程度上取决于装配后的压紧程度，绝缘垫块的弹性系数与此有关。因此，可以通过改变等效的垫块弹性模量来模拟预紧力的大小。

表5～表7和图4～图6数据表明了垫块的个数和尺寸以及预紧力对变压器绕组的固有振动频率的影响。在设计变压器时，应当考虑这几点，使得变压器绕组轴向的固有振动频率避开轴向动态短路力的频率(50Hz或100Hz)。

5 结论

本文基于弹性动力学理论，根据绕组周向垫块弹性支撑等效原则，提出了一种高效的计算电力变压器绕组轴向固有振动频率的二维有限元模型，其固有振动频率的计算具有与三维模型一致的结果，但其计算效率得到大大的提高。同时研究表明，增加垫块的宽度和数量以及增大预紧力都可以提高绕组轴向的固有振动频率，在设计时应当给予考虑，避免绕组产生共振。最后通过对固有振动频率计算的实例校核，验证了本文所提二维模型方法的有效性。

[ 1] 王录亮, 刘文里, 于会凤 (Wang Luliang, Liu Wenli, Yu Huifeng). 电力变压器绕组轴向短路动态力的计算(Calculation of winding axial short-circuit dynamic force of power transformer) [J]. 变压器 (Transformer), 2013,50(1): 14-17.

[ 2] Inge Johansen, Harald Riege. Numerical evaluation of natural frequencies in power transformer windings, power apparatus and systems [J]. Power Apparatus and Systems, Part III - Transactions of the American Institute of Electrical Engineers, 1962, 81 (3): 782-788.

[ 3] 李文海 (Li Wenhai). 变压器短路强度研究成果简介(Brief introduction of achievements in transformer short-circuit strength research) [J]. 变压器 (Transformer), 1997, 34(10):18-22.

[ 4] S K Sahoo, S Gopalakrishna. Winding deformation analysis in power transformers using finite element method [A]. 2014 IEEE Students’ Technology Symposium (TechSym) [C]. 2014. 341-346.

[ 5] 余小辉, 李岩, 井永腾, 等 (Yu Xiaohui, Li Yan, Jing Yongteng, et al.). 变压器绕组模型的固有振动频率计算与分析 (Calculation and analysis of natural frequency of winding model of transformer) [J]. 变压器 (Transformer), 2010, 47(7): 6-8.

[ 6] 邵宇鹰, 饶柱石, 谢坡岸, 等 (Shao Yuying, Rao Zhushi, Xie Poan, et al.). 预紧力对变压器绕组固有振动频率的影响 (The influence of pre-compression changing on the natural frequency of electric transformers windings) [J]. 噪声与振动控制 (Noise and Vibration Control), 2006, 26(6): 51-53.

[ 7] Yan Li, Wei Zhou, Yongteng Jing, et al. Axial vibration analysis of power transformer active part under short-circuit [A]. 2011 International Conference on Electrical Machines and Systems (ICEMS) [C]. 2011.1-4.

[ 8] 汲胜昌, 王俊德, 李彦明 (Ji Shengchang, Wang Junde, Li Yanming). 稳态条件下变压器绕组轴向振动特性研究(Research on axial vibration characteristics of transformer windings under steady condition) [J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2006, 25(1): 35-38, 48.

[ 9] Hadiya Pritesh. Coupled dynamic 3D simulation of short circuit forces [D]. Blekinge Institute of Technology, 2012.

[10] Zhang Bo, Li Yan, Fang Xiaowen. Engineering-oriented research of axial vibration in power transformer windings [A]. 2014 International Conference on Information Science, Electronics and Electrical Engineering (ISEEE) [C]. 2014. 341-345.

[11] 李洪奎,李岩 (Li Hongkui, Li Yan). 不同预紧力下变压器绕组轴向振动模态分析(Axial vibration modal analysis of transformer windings under different levels of pre-compression) [J]. 电机与控制学报 (Electric Machines and Control), 2010, 14(8):98-101, 106.

[12] M R Patel. Dynamic response of power transformers under axial short-circuit force, Part Ⅰ- winding and clamp as individual components [J]. IEEE Transactions on Power Apparatus and Systems, 1973, PAS-92(5): 1558-1566.

[13] M R Patel. Dynamic response of power transformers under axial short-circuit force, Part II - windings and clamps as a combined system [J]. IEEE Transactions on Power Apparatus and Systems, 1973, PAS-92(5): 1567-1576.

Efficient model to calculate axial natural vibration frequency of power transformer winding

LI Kai-qi1, GUO Jian1, LIU Jun2, ZHANG An-hong2, YU Shao-jia2

(1. Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China; 2. Hangzhou Qiantang River Electric Group Co. Ltd., Hangzhou 311243, China)

In the design of transformer winding, natural vibration frequency is an important parameter. Based on the elastic dynamics theory, and according to the elastic support equivalent principle of radial pressboards, a 2D model to calculate axial vibration natural frequency of power transformer winding is presented. The 3D model to calculate natural vibration frequency can be simplified as a 2D one as the support of pressboard on the winding is same. It is tested that results of the 2D model are consistent with those of 3D model, but the former can achieve much higher calculation efficiency. It shows that increasing the width and number of pressboard can improve axial natural frequency through formula analysis and simulation, and also the relations between the changes of axial pre-compression and axial natural vibration frequencies on the windings are investigated. So these factors should be taken into consideration in the design of transformer winding, which can be an effective way to avoid the resonance of winding. Finally, the proposed 2D model’s effectiveness is proved when compared with tested ones.

power transformer; winding; efficient finite element model; axial natural vibration frequency

2015-03-08

国家自然科学基金资助项目(51307082)

李凯琪(1991-)， 女， 江苏籍， 硕士研究生， 研究方向为电力变压器短路强度; 郭 健(1980-)， 男， 山西籍， 副教授， 博士, 研究方向为特种电机的设计。

TM401+.1

A

1003-3076(2016)02-0048-06