电压越限概率指标及其在含风电场电网无功优化控制的应用

原蔚鹏， 王孟邻， 张勇军， 左郑敏， 陈海琼

(1. 广东电网公司湛江供电局， 广东 湛江 524005； 2. 广州供电局有限公司， 广东 广州 510000；3. 华南理工大学电力学院， 广东 广州 510640； 4. 广东电网公司电网规划研究中心， 广东 广州 510080)

电压越限概率指标及其在含风电场电网无功优化控制的应用

原蔚鹏1， 王孟邻2， 张勇军3， 左郑敏4， 陈海琼1

(1. 广东电网公司湛江供电局， 广东 湛江 524005； 2. 广州供电局有限公司， 广东 广州 510000；3. 华南理工大学电力学院， 广东 广州 510640； 4. 广东电网公司电网规划研究中心， 广东 广州 510080)

针对间歇性风电使得基于实时无功优化的电压控制效果劣化问题，提出一种含风电场的无功优化控制模型，用以应对风电功率不确定性对电压控制的影响。根据变速恒频风机有功出力的概率分布，联合风电出力变化与电压变化的关系提出电压越限概率指标及其表达式，基于电压越限概率建立无功优化控制模型。以国内某电网为例，分别应用传统无功优化控制模型和文中所提出的模型进行无功优化控制，并对比其优劣性。结果表明，所提模型不仅能够有效地控制电压，还能降低风电接入下节点电压发生越限的概率。

风电； 威布尔分布； 电压控制； 无功优化控制； 电压越限

1 引言

随着风电场接入容量的增加，风电功率的随机性和间歇性[1]将导致系统电压快速波动。此时，基于定时无功优化计算的自动电压控制系统(Automatic Voltage Control, AVC)将受到很大的影响，以致于达不到其预期的降损和保证电压质量的效果。AVC的控制策略通常由定期(一般控制周期为15～30min)启动的区域无功优化控制策略和随时启动的就地校正策略组成。前者通常是针对电网的潮流断面进行无功优化计算以引导接下来一个周期内的电压趋优控制，而周期内发生的局部电压越限则由后者进行局部调整。然而，由于传统无功优化控制追求降损的结果，往往导致部分节点电压趋近于电压上限，受风电出力频繁波动的影响，这些节点的电压也将随之波动并可能频繁越限。在这种情况下，就地校正策略将频繁操作，影响控制设备的运行寿命、增加系统运行风险。

上述电压控制问题可认为是传统无功优化控制模型对风电场接入的适应性和有效性问题，主要涉及含风电场的潮流计算、无功补偿与规划优化和最优潮流等方面的研究[2-14]，在国内外引起了一定的关注。在含风电场电网的无功优化控制研究中，文献[15]采用无功-电压潮流计算模型和改进的遗传算法求解多目标无功优化模型；文献[16]提出二级协调控制算法，以改进牛顿拉夫逊法为潮流计算手段，并采用遗传算法实现寻优；文献[17]把含双馈电机风电场的配电网无功优化问题转换为一个多约束的非线性混合整数优化数学问题，并采用粒子群优化算法进行求解；文献[18]则利用随机潮流和灰关联遗传算法对含风电场的电网进行无功电压控制。现有文献的研究主要侧重于风电在潮流计算中的模型和求解算法的改进，而较少涉及无功优化控制模型本身。

本文提出一种基于电压越限概率(Probability of Voltage Violation, PVV)指标的含风电场无功优化控制模型。该模型采用PVV指标反映节点电压在风电影响下发生越限的概率，并通过优化计算使节点的PVV指标达到最小。

2 基于电压越限概率的无功优化控制模型

2.1 电压越限概率的物理意义分析

风电场一般位于偏远地区，远离负荷中心，并通过一条线路接入最近的同电压等级的变电站实现并网，形成链式网络，如图1所示。

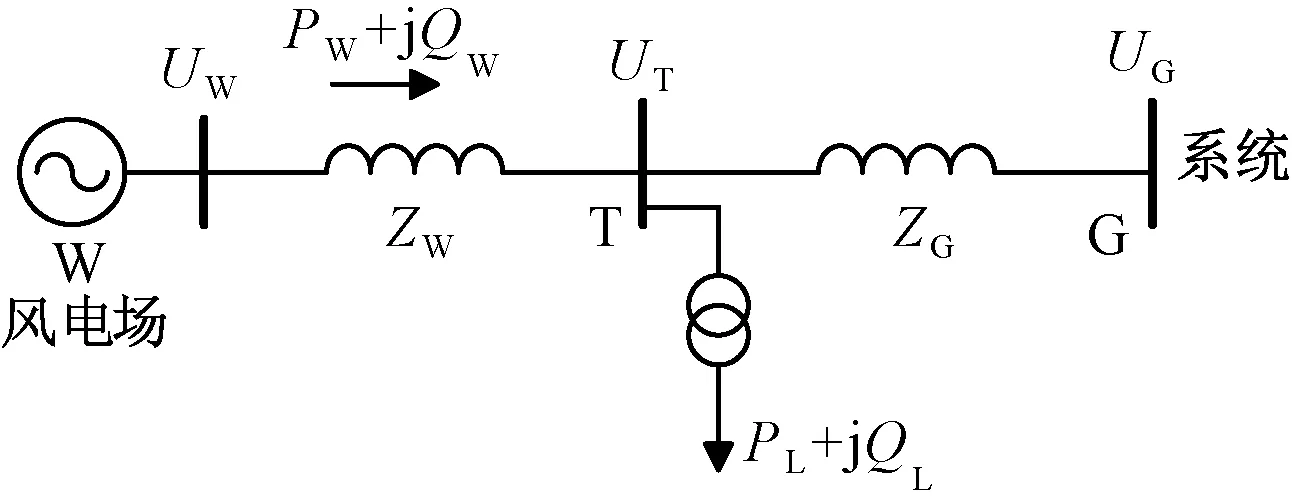
图1 风电场并网示意图Fig.1 Sketch of wind farm connected to grid

图1中，T为风电场W并网连接的变电站，G为高一电压等级的等值大系统，PL、QL分别为变电站T的有功和无功负荷，PW、QW分别为风电场有功和无功出力，ZW为风电场到变电站T间的等效阻抗，ZG=RG+jXG为变电站T与等值系统之间的等效阻抗，UT为变电站T高压母线电压，UW为风电场高压母线电压，UG为等效系统电压，在无功优化控制的一个间隔时间内UG可视为恒定且不受风电出力的影响。

忽略电压降的横分量和线路上的功率损耗，由图1可得：

(1)

(2)

则由于风电场出力波动造成变电站T的电压波动量为

(3)

可见，随着风电场出力的波动，链式电网中变电站的电压波动量将大致与风电出力波动量成正比。文献[19]的仿真结果也反映了这个近似规律，同时表明对离风电场较远的节点也具有相同的规律。即若风电场以恒定功率因数运行，则相对风电零发的情况，风电有功出力的增量与区域内节点电压的增量呈近似线性关系，对某一风电场j，有

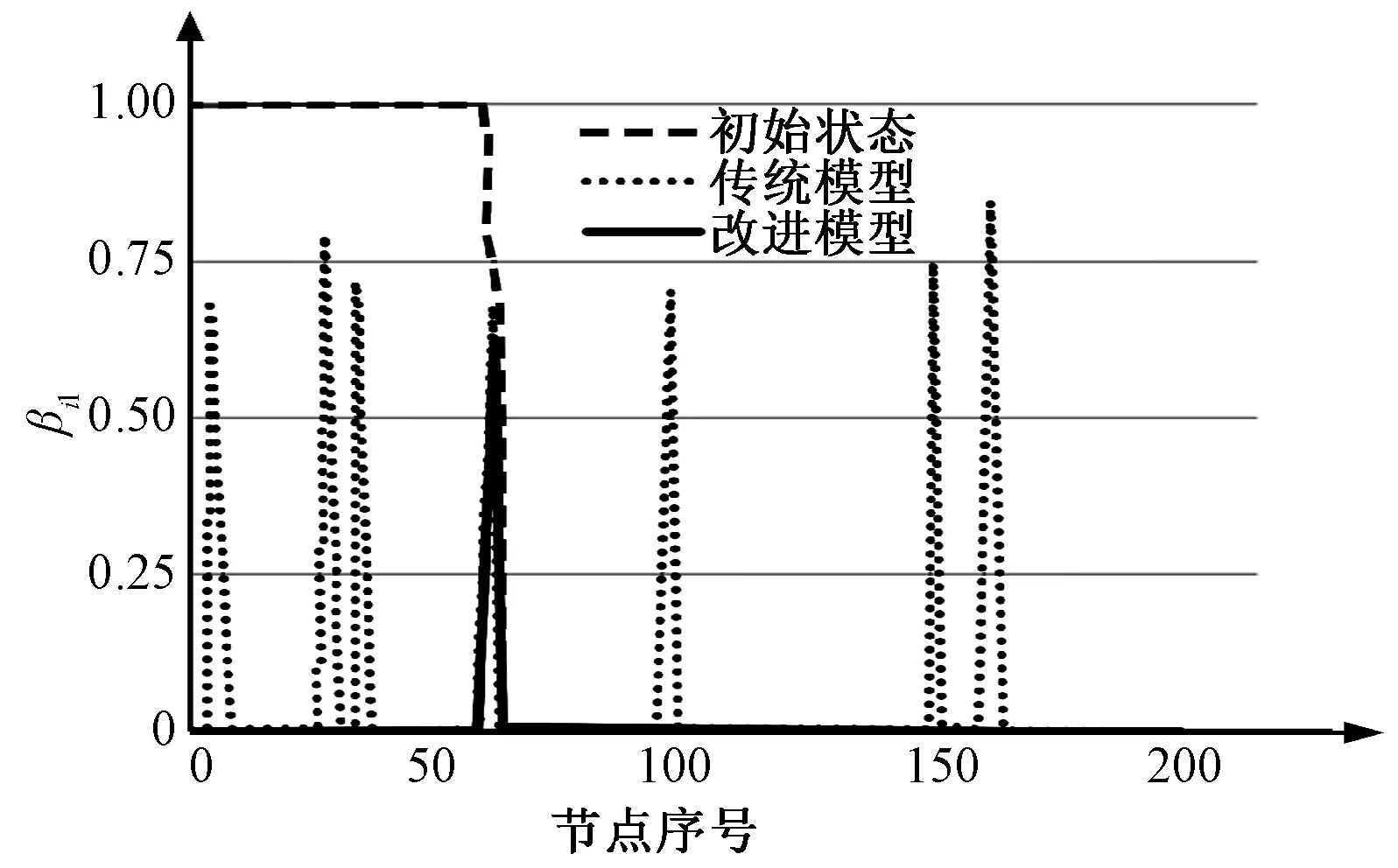
(4)

式中，Pj为风电场j的有功出力；Pj0为风电场j零发时的出力，可近似取值为0；Kij为风电场j单独作用下其出力对节点i的电压影响因子；ΔUij为节点i的电压随风电场j出力变化而产生的变化量。根据式(3)，因高压电网中通常满足RG<

同时，考虑到风电场对电压的影响主要是风电场无功的影响，在分析中一般采用风电场运行中所规定的最低功率因数。在这种情况下，风电场对电压的影响最大，可作为极端情况。

假设风电场j以滞后功率因数运行，则风电场j由零发变化为满发或由满发到零发时，节点i的电压变化量最大，记该变化量为ΔUiMax，同时记节点i的允许电压运行上下限为UiMax和UiMin。图2表示风电场出力波动与节点i电压变化的关系。

图2 风电功率与节点电压关系Fig.2 Relation of wind power and node voltage

由图2可知，当AVC无功优化控制后得到的节点电压位于区间[UiMin+ΔUiMax,UiMax-ΔUiMax](即斜线区域Aij)时，无论风电场出力多少，状态如何变化，在AVC的一个控制周期内，节点电压不会发生越限，越限的概率为0。然而，当风电场j容量较大时，Aij区域未必存在；即使Aij区域存在，由于无功调节资源有限，电压不一定都能调节到Aij区域内，而可能落在图2中的灰色区域。此时，节点电压受风电影响具有一定的概率发生越限，记该概率的最大可能值为电压越限概率PPVV。

定义：电压越限概率为稳态工况下，在AVC的一个控制周期内，受风电场j的出力影响，电网节点i电压发生越限的最大可能概率，记为βij。

2.2 考虑电压安全性的无功优化控制模型

传统的无功优化控制模型是一个复杂的多变量、多约束、非凸性的非线性混合整数规划问题[20]。通过无功优化计算可以得到某一潮流断面下无功控制设备的最优配置，从而达到使电压合格和降损的目的。传统无功优化控制模型的目标函数为

minf=PL

(5)

式中，PL为全网有功损耗。

同时，无功优化控制模型还需要考虑潮流方程约束、节点电压运行范围约束、无功电源无功出力范围约束、无功补偿设备的无功出力约束以及变压器的调档范围约束等。

传统无功优化控制模型适用于电网负荷缓慢变化下的电压控制。然而，由于风电场为电压控制带来了很大的不确定性，传统模型针对线损的优化将很可能达不到应有的效果。而且，考虑到风电场出力的随机特性对电压波动的影响，无功优化控制应首要解决电压的安全性问题，即应使节点受风电场影响而发生电压越限的概率降到最低。因此，引入电压越限概率指标作为无功优化控制的目标函数更为合适。则新的无功优化控制目标函数为

(6)

式中，N为电网节点编号集。

该式以最小化βij最大值为优化目标，从而保证所有βij均处于较低水平。

本文所提的无功优化控制模型以节点电压越限概率最大值最小化取代了传统以网损最小化为目标，而约束条件沿用传统的无功优化控制方法，即潮流方程约束、节点电压运行范围约束、无功电源无功出力范围约束、无功补偿设备的无功出力约束以及变压器的调档范围约束等[20]。

下文将详细介绍PVV的推导和求解。推导的过程仅限于变速恒频风机。

3 电压越限概率指标的计算方法

3.1 变速恒频风机的有功出力概率分布

根据变速恒频风机的有功出力与风速的关系[13,21]和风速概率分布双参数威布尔分布[21-23]，可得风机有功出力的累积概率为

(7)

式中，x为风机的实时出力；P为设定的风机有功出力值；vin和vout分别为风机的切入和切出风速；c为尺寸参数；k为形状参数；P1为风速为vin时风机的输出功率；Cp为风能转换效率；A为风轮扫风面积；G为风轮轮毂高度处的空气密度；PN为额定功率。

3.2 电压越限概率的计算

式(4)中的Kij为一估算量，可以通过进行2次潮流计算进行近似计算。假设风电场j以某一滞后功率因数运行。首先，使风电场j的有功出力为0，为电网进行第1次潮流计算，并记录相应电压结果；然后，使风电场j的出力增加到PNj(即风电场j的额定容量)并保持其他参数不变，进行第2次潮流计算以得到相应的电压结果。将第2次潮流的电压结果减去第1次潮流的电压结果，可得到节点i的电压变化量，记为ΔUijmax。将PNj和ΔUijmax代入式(4)，可求得Kij。

由于风电有功出力波动与区域内节点电压增量为近似线性关系，全体风电场对节点i的电压影响因子[24]为

(8)

式中，nW为风电场个数。

由于各风电场出力对电压的影响为近似线性关系，则当节点i在所有风电场影响下变化ΔUi时，风电场j引起的电压变化量所占百分比为

(9)

则对某一确定的节点i的电压值，可以通过换算得到风电场j导致其越上限的出力增量为

(10)

导致其越下限应有的出力减量为

(11)

再令Ui0为电压运行范围的中值。即

(12)

则当UiMax-ΔUijMax大于Ui0时，图2中的Aij区域存在。由式(7)～式(11)可得：

(13)

式中，ρ(*)表示引用式(7)的函数计算方法。

当UiMax-ΔUijMax小于Ui0时，图2中的Aij区域不存在。由式(7)～式(12)可得：

(14)

4 实例分析

选择2011年度国内某城市电网夏季大方式为例(接线示意如图3所示，电网包含2座在运行风电场1和2，装机容量均为49.5MW，由于网架数据量较大，不在文中列出)，分别应用式(5)所示的传统无功优化控制模型和本文提出的模型进行无功优化控制，并采用灾变遗传算法[25]求解以对比其优劣性。

图3 电网接线示意Fig.3 Sketch of power networks

4.1 参数计算

4.1.1 计算电压影响因子

根据风电场并网协议，风电场应以大于0.95的功率因数运行。由于风电场以滞后0.95功率因数运行时对电网电压影响最大，下文根据这种运行方式计算节点i的电压影响因子Ki、风电场1和风电场2的电压影响因子Ki1和Ki2；由于数据量大，Ki、Ki1和Ki2的计算结果不在文中列出。

4.1.2 计算风机参数

风电场1和2各配置33台MY1.5s双馈风力发电机，风机的主要技术参数为: 额定功率1.5MW；风轮直径77.36m；扫风面积4638m2；额定风速10.3m/s；切入风速3m/s；切出风速25m/s。

取空气密度为一个大气压下、20℃时的空气密度，即1.205kg/m3。由式(4)可得，Cp约为0.4912。

4.1.3 拟合风电有功出力概率分布

截取风电场1在2011年共105120个采样点(5min一个采样点)的有功出力数据，如图4所示。

图4 风电场1有功出力Fig.4 Power output of wind farm 1

采用Matlab仿真工具进行概率分析，其概率分布曲线如图5中虚线所示。采用式(7)和最小二乘法进行拟合，得到理论尺寸参数c为10.818，形状参数k为2.842，拟合曲线如图5中实线所示。

图5 风电场有功出力概率分布和拟合Fig.5 Probability distribution fitting of wind power

由图5可见，大部分情况下拟合的误差都很小，这也验证了式(7)的正确性。同理，也可对风电场2做同样的分析。

4.2 无功优化控制结果分析

图6 各110kV变电站的节点电压分布对比Fig.6 Comparison of voltage profile of 110kV substations

分别采用传统以网损最小化为目标的静态无功优化控制模型[20]和本文提出的改进模型对该电网2011年夏季大方式进行计算，风电场以额定出力和0.95的滞后功率因数运行。得到优化电压结果如图6所示。由图6可见，两种无功优化控制均能在当前潮流断面下很好地控制当前时刻的电压在合格范围内。然而传统模型并未就风电的状态变化进行考虑。要适应风电的波动特性，仅对当前潮流断面的电压进行控制是不够的。

以风电场1为例，βi1(i∈N)的计算结果如表1和图7所示。

表1 结果对比

注:βi1平均值指的是β11、β21、…、βn1的平均值(n为电网节点数)。

图7 节点电压越限概率βi1对比Fig.7 Comparison of probability of voltage violation βi1

由表1可见，改进模型较传统模型的βi1平均值下降89%。而由图7可见，初始状态下一部分节点的βi1为1，而经过传统模型优化以后，βi1较高的节点为9个，这意味着无功优化控制后的一段时间里系统将有多个节点存在很大的可能发生电压越限，而改进模型只存在1个βi1较高的节点。可见，改进模型能够更好地适应风电功率随时间的波动。

5 结论

本文建立了一种基于电压越限概率的含风电场电网无功优化控制模型和方法，用以应对风电场功率波动性和间歇性所带来的电压控制问题。仿真分析结果表明传统模型的优化结果在应对风电功率波动时存在不足，而本文所提模型和方法能够显著降低风电波动导致节点电压越限的风险，避免电压调控设备频繁操作，兼顾了系统运行安全性与经济性的需要，使AVC对风电接入的适应性显著提高。

[ 1] Glinkowski M, Hou J, Rackliffe G. Advances in wind energy technologies in the context of smart grid [J]. Proceedings of the IEEE, 2011, 99(6): 1083-1097.

[ 2] 董雷，程卫东，杨以涵 (Dong Lei, Cheng Weidong, Yang Yihan). 含风电场的电力系统概率潮流计算(Probabilistic load flow calculation for power grid containing wind farms) [J].电网技术 (Power System Technology)，2009，33(16)：87-91.

[ 3] 李强，李凤婷，樊艳芳，等 (Li Qiang, Li Fengting, Fan Yanfang, et al.). 风电并网对接入地区电压的影响(Voltage influence of wind power integration) [J]. 中国电力 (Electric Power)，2012，45(4)：15-18.

[ 4] 董炜，余健明，杨濛濛 (Dong Wei, Yu Jianming, Yang Mengmeng). 含风电场配电网随机潮流计算及其电压安全分析 (Voltage security analysis on the distribution network with the integration of wind power by using stochastic power flow) [J]. 中国电力 (Electric Power)，2012，45(4)：82-86.

[ 5] 张强，仇卫东 (Zhang Qiang, Qiu Weidong). 风电场内集中无功补偿容量的设计与研究 (Design of centralized reactive power compensation capacity of the wind farm) [J]. 中国电力 (Electric Power)，2012，45(9)：25-28.

[ 6] 江岳文，陈冲，温步瀛 (Jiang Yuewen, Chen Chong, Wen Buying). 随机模拟粒子群算法在风电场无功补偿中的应用(Application of stochastic simulation’s particle swarm algorithm in the compensation of reactive power for wind farms) [J].中国电机工程学报(Proceedings of the CSEE)，2008，28(13)：47-52.

[ 7] Hong Y, Pen K. Optimal VAR planning considering intermittent wind power using Markov model and quantum evolutionary algorithm [J]. IEEE Transactions on Power Delivery, 2010, 25(4): 2987-2996.

[ 8] Hetzer J, Yu D C, Bhattarai K. An economic dispatch model incorporating wind power [J]. IEEE Transactions on Energy Conversion, 2008, 23(2): 603-611.

[ 9] Liu X, Xu W. Economic load dispatch constrained by wind power availability: a here-and-now approach [J]. IEEE Transactions on Sustainable Energy, 2010, 1(1): 2-9.

[10] 刘沛津，谷立臣 (Liu Peijin, Gu Lichen). 含风电场的电力系统无功规划优化 (Optimization of reactive power planning for power system containing wind farms) [J]. 电网技术 (Power System Technology)，2010，34(7)：175-180.

[11] 温步瀛, 江岳文，陈冲 (Wen Buying, Jiang Yuewen, Chen Chong). 风电场并网运行的无功补偿优化问题(Reactive power compensation optimization for grid-connected wind farm) [J]. 电力自动化设备 (Electric Power Automation Equipment)，2008，28(5)：42-46.

[12] 张瑞华，宋云亭 (Zhang Ruihua, Song Yunting). 基于蒙特卡罗仿真和电压安全约束的无功优化算法(Voltage security constrained reactive power optimization based on Monte-carlo simulation) [J]. 电力系统自动化(Automation of Electric Power Systems)，2002，26(7)：23-27.

[13] 郑太一，焦邵华，赵会龙，等 (Zheng Taiyi, Jiao Shaohua, Zhao Huilong, et al.). 基于准定向变异和变异回滚微分算法的风电场无功补偿 (Quasi-directional variation and rollback mutation based differential evolution algorithm for reactive power compensation of wind farms) [J]. 中国电力 (Electric Power)，2013，45(5)：71-76.

[14] 陈琳，钟金，倪以信，等 (Chen Lin, Zhong Jin, Ni Yixin，et al.). 含分布式发电的配电网无功优化(Optimal reactive power planning of radial distribution systems with distributed generation) [J]. 电力系统自动化 (Automation of Electric Power Systems)，2006，30(14)：20-24.

[15] 魏希文，邱晓燕，李兴源，等 (Wei Xiwen, Qiu Xiaoyan, Li Xingyuan, et al.). 含风电场的电网多目标无功优化(Multi-objective reactive power optimization in power system with wind farm) [J]. 电力系统保护与控制 (Power System Protection and Control)，2010，38(17)：107-111.

[16] 罗雨蕾，李妍，吴琨 (Luo Yulei, Li Yan, Wu Kun). 含风电电网的动态全局最优潮流及其两级协调控制算法(Dynamic global optimal power flow and its two-stage control algorithm of a power grid integrated wind power farms) [J]. 中国电力 (Electric Power)，2013，45(9)：131-137.

[17] 赵晶晶，符杨，李东东 (Zhao Jingjing, Fu Yang, Li Dongdong). 考虑双馈电机风电场无功调节能力的配电网无功优化 (Reactive power optimization in distribution network considering reactive power regulation capability of DFIG wind farm) [J]. 电力系统自动化 (Automation of Electric Power Systems)，2011，35(11)：33-38.

[18] Hong Y, Pen K. Optimal VAR planning considering intermittent wind power using Markov model and quantum evolutionary algorithm [J]. IEEE Transoctions on Power Delivery, 2010, 25(4): 2987-2996.

[19] 张立梅，唐巍，赵云军，等 (Zhang Limei, Tang Wei, Zhao Yunjun, et al.). 分布式发电接入配电网后对系统电压及损耗的影响分析 (Analysis of DG influences on system voltage and losses in distribution network) [J]. 电力系统保护与控制 (Power System Protection and Control)，2011，39(5)：91-96.

[20] 张勇军，俞悦，任震，等 (Zhang Yongjun, Yu Yue，Ren Zhen, et al.)．实时环境下动态无功优化建模研究(Modeling of dynamic reactive power optimization under real -time circumstance) [J]. 电网技术 (Power System Technology)，2004，28(12)：12-15.

[21] Yeh T H, Wang L. A study on generator capacity for wind turbines under various tower heights and rated wind speeds using Weibull distribution [J]. IEEE Transactions on Energy Conversion, 2008, 23(2): 592-602.

[22] Albadi M H, El-Saadany E F. Wind turbines capacity factor modeling — a novel approach [J], IEEE Transactions on Power Systems, 2009, 24(3): 1637-1638.

[23] Villanueva D, Feijoo A, Pazos J L. Simulation of correlated wind speed data for economic dispatch evaluation [J]. IEEE Transactions on Sustainable Energy, 2012, 3(1): 142-149.

[24] 王孟邻 (Wang Menglin). 含风电场电网的无功电压运行与规划研究 (Research on Var/Volt operation and reactive power planning of power grids with wind farms) [D]. 广州：华南理工大学 (Guangzhou: South China University of Technology), 2013.

[25] 张勇军 (Zhang Yongjun). 电力系统无功优化的灾变遗传算法及MAS模型研究 (Cataclysmic genetic algorithm and MAS based model for reactive power optimization of power systems) [D]. 广州：华南理工大学 (Guangzhou: South China University of Technology)，2004.

(，cont.onp.80)(，cont.fromp.67)

Probability of voltage violation and its application on optimal reactive power control of power grids with wind farms

YUAN Wei-peng1, WANG Meng-lin2, ZHANG Yong-jun3, ZUO Zheng-min4, CHEN Hai-Qiong1

(1. Zhanjiang Power Supply Bureau, Guangdong Power Grid Co., Zhanjiang 524005, China; 2. Guangzhou Power Supply Co., Ltd., Guangzhou 510000, China; 3. School of Electric Power, South China University of Technology, Guangzhou 510640, China; 4. Planning Research Center, Guangdong Power Grid Co., Guangzhou 510080, China)

The intermittent wind power deteriorates the voltage control based on real-time reactive power optimization. This paper has proposed an optimal reactive power control model to deal with the impact of wind power on voltage security. The probability of voltage violation (PVV) is calculated by combining the probability of power output of variable speed constant frequency wind turbine and the relationship between the power output of wind farm and voltage of the grid. And a model of optimal reactive power control is put forward base on the PVV. Taking a power grid in China as a case, a tradition model of optimal reactive power control and the model proposed in this paper are put into practice and comparisons are made between both models. The comparison shows that the model proposed in this paper can not only control the voltage well, but also lower the probability of voltage violation caused by wind power fluctuation.

wind power; Weibull distribution; voltage control; optimal reactive power control; voltage violation

2014-10-20

国家自然科学基金资助项目 (51377060)

原蔚鹏 (1979-), 男, 山东籍, 高级工程师, 硕士, 从事电网规划的研究和管理工作; 张勇军 (1973-), 男, 广东籍, 教授, 博士, 研究方向为电力系统无功优化规划与控制、 电力系统可靠性等。

TM614； TM714

A

1003-3076(2016)02-0062-06