基于FFT和优化匹配追踪的谐波/间谐波检测
2016-05-25郑德忠赵兴涛廖文喆
陈 雷, 郑德忠, 赵兴涛, 廖文喆
(1. 燕山大学电气工程学院, 河北省测试计量技术及仪器重点实验室, 河北 秦皇岛 066004; 2. 东北石油大学秦皇岛分校, 河北 秦皇岛 066004; 3. 河北工业大学控制科学与工程学院, 天津 300130)
基于FFT和优化匹配追踪的谐波/间谐波检测
陈 雷1, 2, 郑德忠1, 赵兴涛1, 廖文喆3
(1. 燕山大学电气工程学院, 河北省测试计量技术及仪器重点实验室, 河北 秦皇岛 066004; 2. 东北石油大学秦皇岛分校, 河北 秦皇岛 066004; 3. 河北工业大学控制科学与工程学院, 天津 300130)
谐波和间谐波干扰严重影响电力系统的正常运行,将快速傅里叶变换(FFT)和采用局部优化的匹配追踪算法相结合,并构造离散正弦字典,实现在含有噪声、基波频率偏移和频率相近的间谐波情况下的谐波和间谐波参数检测。采用循环迭代方法,按照能量大小,依次提取出谐波和间谐波扰动成分,每次迭代首先用FFT估计出当前频率参数,并搜索该频率下的相位,然后以该频率和相位作为初值,用Nelder-Mead算法获得优化后的频率和相位值,并通过MP算法提取出匹配信号表达式,进而获得幅值参数。仿真结果表明本文提出的算法计算复杂度低、物理意义清晰,具有较好的检测精度和抗噪性能。
谐波; 间谐波; 匹配追踪; 正弦字典; 时频原子; 优化计算
1 引言
电力系统中的电弧炉、电动机、变压器等波动性、冲击性负荷及各种现代电力电子设备的大量应用,导致谐波、间谐波的频繁发生,对电网的正常运行造成很大危害,如引起电压波动及照明设备的闪变现象,导致仪器测量结果不准确,引起电动机的噪声和振动,导致电力系统发电机组的次同步振荡等问题。因此对谐波和间谐波的精确检测引起了人们的很大关注。
目前,国内外学者已提出了很多谐波、间谐波检测方法,主要有FFT法[1]、小波分析法[2]、希尔伯特黄变换(HHT)[3]、Prony算法[4]、AR模型谱估计法[5]、MUSIC法[6]、ESPRIT法[7]、Wigner-Ville分布(WVD)方法[8]等。但FFT存在频谱泄漏和栅栏效应,小波法有小波基有效选取等问题,HHT方法存在端点效应和模态混叠,Prony和AR模型法对噪声敏感,MUSIC等谱估计法的实时性不好,WVD法有交叉干扰问题,以上问题是这些方法有效应用的障碍。目前随着电力系统的负载和供电方式的多元化和复杂化,为了适应现代谐波/间谐波检测的需要,人们不断对已有方法进行改进和完善,并继续研究新的测量方法和手段。
近年来,基于过完备字典稀疏分解的信号处理方法逐渐被应用到电力系统信号处理领域[9-11],其中文献[10]采用Gabor时频原子方法分析间谐波,但存在计算量大的问题;文献[11]采用基于粒子群优化(Particle Swarm Optimization,PSO)的匹配追踪(Matching Pursuit,MP)分解算法实现了间谐波参数的快速检测,但算法受采样频率和信号长度影响很大,不具普遍性。本文基于信号稀疏分解思想,采用MP算法,在正弦字典下对含有谐波和间谐波扰动的信号进行迭代分解,按照能量大小逐次提取出波形特征参数,通过与局部优化算法的结合,实现了噪声背景下对谐波和间谐波的幅值、频率和相位的快速准确检测,且不受非同步采样和信号频率成分的限制。
2 基于过完备字典的匹配追踪分解算法
2.1 过完备字典的概念
过完备字典是一组具有广泛时频特性的函数波形,每个波形作为字典中的一个元素,称为时频原子,字典中的原子数量应是高度冗余的,以便精确捕捉信号的各种局部特征。与传统的基于正交基的分解方法不同,基于过完备字典的分解能够根据信号的结构特征,实现对信号的自适应分解,从而获得更加简洁的表达。
2.2 匹配追踪分解
过完备字典下的MP分解是一种贪婪迭代分解算法,其目的是用字典中尽量少的原子组合,以尽量小的误差表达信号。
定义过完备字典D={gγ}γ∈Γ,其中Γ为原子参数组γ的集合,gγ为字典中的原子,且有‖gγ‖=1,MP的分解方法如下:
假定第n≥0阶残差为Rn,令R0=f,选择gγn∈D,使得内积绝对值|
(1)
n阶残差Rn按式(2)分解为:
(2)
当分解到m阶时,信号f被分解成式(3)中和的形式:
(3)
根据式(2)可得:
(4)
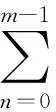
可见,MP算法通过以上贪婪迭代过程,在字典中寻找与被分解信号f最匹配的原子,当分解到m阶时,得到m个匹配原子,则信号可用这m个原子的线性组合来表示,组合系数即为每次迭代对应的内积值
2.3 正弦字典
已提出的几种常用字典包括Gabor字典、小波包字典、衰减正弦字典和Chirp字典等。用来分解信号的字典中原子的时频特性应与被分解信号的局部结构相适应,电力系统谐波、间谐波信号实际上是一系列正弦曲线波形,为此这里构造正弦量字典,其原子的复数表达式为:
(5)
实数表达形式为:
(6)
式中,K为原子的归一化幅度值;ω为频率;φ为相位;γ=(ω,φ)为原子的时频参数组索引,用以表征谐波和间谐波扰动信号的特征。
对于以上连续参数的过完备正弦字典D,其原子数量是无限的,而MP算法需要与过完备字典中的所有原子计算内积,以确定匹配原子参数,因此,要有效应用MP分解,必须对原子参数离散化,即构造子字典Dα=(gγ)γ∈Гα∈D,Гα为包含在Г中的有限索引集,参照文献[12]提出的Gabor原子参数离散化方法,对正弦原子参数做如下离散化处理:
(7)
式中,Δφ=π/6;Δω=π;0≤k<2j+1;0≤i≤12;0 在离散正弦字典上对含有谐波和间谐波的信号进行MP分解时,由于字典的离散化和迭代算法中的误差累积效应,使得提取出的谐波和间谐波参数误差较大。为了提高算法的分解速度和谐波、间谐波的参数估计精度,本文在MP分解中引入快速傅里叶变换(FFT)和局部极值优化算法,这里将其简称为FFT-LOMP (FFT Local Optimization Matching Pursuit) 算法。 3.1 谐波/间谐波匹配参数的初步估算 MP分解通过在给定的字典中寻找与当前残差的内积的绝对值最大的原子作为匹配原子,这里首先利用FFT寻找能量最大成分的频率值。设采样频率为fs,信号的长度为N。每次迭代,通过FFT获得当前残差中能量最大成分对应的谱线序列为λ,该谱线对应的频率ωλ为: (8) 通过这种频率预计算,确定原子的频率参数,然后在频率ωλ下,按照相位离散化表达式iΔφ,搜索使原子与残差内积绝对值最大的相位参数φλ。这里仅用FFT进行频率和相位的预估,后续将采用优化计算法对其进行校正,因此FFT中频谱泄漏和栅栏效应引起的误差对最终计算结果影响很小。 3.2 谐波/间谐波匹配参数的优化计算 根据式(1)可知,使用MP算法搜索匹配原子参数,需要求| (9) 由于已经确定了频率和相位的离散化估计值ωλ和φλ,可将(ωλ,φλ)作为原子参数的初值,利用优化算法在该初值附近求解如下极小值问题: (10) 求解该类问题,可以考虑最速下降法、牛顿法、共轭梯度法、拟牛顿法以及Nelder-Mead算法。其中Nelder-Mead(NM)算法是一种局部搜索算法,该算法使用直接搜索策略,无需目标函数的任何导数信息,不涉及到复杂的Hessian矩阵运算,计算工作量小,尤其适合于变量不是很多的极值求解问题。 NM算法借助单纯形的思想,仅利用目标函数值的信息,通过反射、扩张、压缩和整体收缩四种运算寻找最优解。下面介绍离散正弦字典下,基于NM算法实现谐波和间谐波匹配参数的优化计算过程。 对于目标函数的n个变量,首先确定其初始值,并在其初始值附近构造出n维单纯形的n+1个顶点xi(i=1,2…n+1)作为目标函数的初始解集,每个顶点是由目标函数的n个变量构成的一个n维向量,以上初始工作完成后,执行如下迭代过程。 (1) 计算n+1个顶点的目标函数值F(xi),依据目标函数值从小到大对顶点排序,排序后顶点应满足F (x1)≤ F (x2) ≤…≤F (xn)≤F(xn+1),x1为最优顶点,xn+1为最差顶点。 (4) 取扩张系数μ=2,压缩系数ε=0.5,整体收缩系数σ=0.5。根据F (xr)与顶点目标函数值的大小关系,通过扩张、压缩和整体收缩的运算,得到一个新的n 维单纯形,用作下次迭代。 (5) 误差足够小或达到指定迭代次数,则停止迭代,并输出最优顶点x1,作为匹配原子参数。否则返回步骤(1)继续迭代。 这里的每个向量由正弦原子的2维参数ω、φ的值构成,即取n =2,初始值为(ωλ,φλ)。按照以上过程即可求得满足式(10)的优化的频率ωλn和相位φλn,以及对应的复数形式归一化匹配原子: (11) 进而求得当前迭代提取出的谐波或间谐波的频率ωn和相位φn: (12) (13) 从而得到归一化原子的实数表达: (14) 再利用式(14)的结果进一步计算幅值参数: (15) 3.3 FFT-LOMP谐波/间谐波检测步骤 FFT-LOMP方法按照以下步骤依次提取出谐波/间谐波扰动参数。 (1)采用FFT获得频谱幅度最大频率的初步估计值ωλ。 (2)在离散正弦字典中,遍历搜索使原子与残差的内积绝对值最大的相位参数φλ。 (3)以ωλ和φλ为初值,采用NM算法获得优化的频率ωλn和相位φλn。 (4)按照式(12)和式(13)恢复实际频率ωn和相位φn,并得到归一化原子的实数表达gγn(t)。 (5)获得本次迭代提取出的匹配扰动表达式 (6)根据式(2)计算当前迭代的残差Rn,当残差小于指定阈值或达到指定迭代次数则停止迭代,否则再次执行步骤(1)~步骤(6)。 国标GB/T 15945-2008规定电力系统正常运行时的基波频率偏差限值为±0.2Hz,电能质量测量时的基波频率测量误差不应超过±0.01Hz。国标GB/T 14549-1993规定各次谐波测量的幅度误差不大于±5%,角度误差不大于±5°。在Matlab 2012仿真平台下,构造电力系统信号,采样频率fs=3200Hz,数据长度N=1024,采用标幺值(pu)作为幅度单位。 噪声是一种有害的、频率在200kHz以内的频谱范围很宽的电气信号,其叠加在电力系统中性线、相线或信号线的电压或电流上,包含了除谐波失真或暂态扰动的所有电力信号扰动。噪声的频率和幅值取决于噪声源及系统特性,根据IEEE 标准,噪声的典型幅值低于电压幅值的1%,对应信噪比(SNR)为40dB,这里在信号中加入高斯白噪声,验证所提出的方法在噪声下的参数检测性能。 4.1 仿真算例1 采用文献[13]中提出的算法和仿真模型,对本文的FFT-LOMP算法和基于主特征值倒数加权信号子空间投影的多重信号分类算法RWSP-MUSIC、基于总体最小二乘旋转不变技术算法TLS-ESPRIT、MUSIC算法进行对比,SNR为65dB。得到频率参数的估计值和估计误差分别如表1和表2所示。 表1 频率参数估计值 表2 频率参数估计误差 由表1和表2可见,采用本文提出的FFT-LOMP算法,除了对79Hz低频间谐波的频率估计误差为0.0209%以外,对其他分量的频率估计误差均在0.01% 以内,虽然对205Hz和250Hz的估计精度略低于RWSP-MUSIC,但本文算法对所有频率成分的平均估计误差仅为0.0076%,远低于其他三种算法。因此总体而言,本文算法更优。 4.2 仿真算例2 电力系统正常运行时的频率偏差限值规定为±0.2Hz,即频率为49.8~50.2Hz。设被测信号含有2~5次谐波和142Hz、154.5Hz间谐波。表3给出了基波频率为49.8Hz和50.2Hz两种情况下谐波、间谐波的参数设置,表4给出了频率、幅值、相位的估计值和估计误差。 表3 参数设置 可见,基波频率分别为49.8Hz和50.2Hz时的频率估计绝对误差分别为0.0033Hz和0.0052Hz,基波幅值的估计误差都小于0.1%,均在国标规定范围内;除49.8Hz时的3次谐波以外,其他谐波和间谐波的幅值估计误差均小于2%,谐波的频率估计误差均小于0.02%,间谐波的频率估计误差都在0.07% 以内;5次谐波相位误差稍大,其余谐波相位估计误差均在1°以内,两个间谐波的相位估计误差较大,在5°以内。总体而言,在基波频率偏差限值内,本文算法可以较准确地检测基波及对应的谐波的幅值、频率、相位参数,并有效分辨出与3次谐波接近的间谐波。 表4 基波频率偏移的谐波、间谐波参数估计结果 4.3 仿真算例3 设原始信号基波频率为50Hz,含有2、3、5、7次谐波和32Hz、54.5Hz的间谐波,其中54.5Hz与基波频率接近,仿真检测结果如表5所示。可见算法对谐波频率的估计误差都在0.004% 以内,对低频间谐波的频率估计误差都在0.08%以内;初相位的估计误差均小于1°;对幅值很小的间谐波的幅值估计误差稍大,为1.25%,对其它幅值的估计误差在0.4% 以内;同时算法很好地分辨出了和基波频率相近的54.5 Hz间谐波频率成分。 为检测算法的抗噪性能,这里在上述信号中叠加高斯白噪声,测试SNR 为35dB、30dB、25dB 的几种更严重的噪声水平下的算法检测性能。参数估计值如表6所示,估计误差如表7所示。可见,SNR为35dB和30dB时,参数的估计误差都小于国标规定值,整体保持了较高的精度,具有较好的抗噪性能,当SNR降为25dB时,幅值和相位估计精度降低,但频率估计精度仍较高。 表5 不含白噪声的谐波、间谐波参数估计值 表6 含白噪声的谐波、间谐波参数估计值 表7 含白噪声的谐波、间谐波参数估计误差 4.4 电弧炉信号分析 考虑文献[14]中的如下实际电弧炉信号: x(t)=100cos(100πt+20°)+ 74.813cos(250πt+9°)+ 64.933cos(50πt+93°)+δ(t) (16) 其中含有50Hz基波和125Hz、25Hz的间谐波,以及5%的随机白噪声干扰δ(t),信噪比约为26dB。采用本文方法对其进行分解,波形如图1所示。检测到的波形参数如表8所示。其中u1、u2和u3为分解出的电弧炉信号中的三种频率成分,对其进行重构后的信噪比可达到45dB以上,u4为分离出的含白噪声的残差信号。检测结果体现出了较高的检测精度和抗噪性能。 图1 电弧炉波形分解Fig.1 Arc furnace waveforms decomposition 检测值检测误差幅值(pu)频率/Hz相位/(°)幅值(%)频率(%)相位/(°)u199.934549.998319.87920.06550.00340.1208u274.8879125.00538.85340.10010.00420.1466u364.925225.000292.85350.01200.00080.1465 本文提出的FFT-LOMP谐波和间谐波检测方法具有清晰的物理意义,可以同时实现对谐波和间谐波的幅值、频率和初始相位的检测,并可有效分辨出与基波或谐波频率相近的间谐波成分,且检测精度受基波频率偏移的影响较小,同时算法具有较好的抗噪性能。本方法对频率邻近成分的相位检测精度 还有待进一步提高,另外在此方法的基础上实现暂态谐波/间谐波的检测也是下一步要做的工作。 [ 1] 祁才君, 王小海 (Qi Caijun, Wang Xiaohai). 基于插值FFT算法的间谐波参数估计(Interharmonic estimation based on interpolating FFT algorithm) [J]. 电工技术学报(Transactions of China Electrotechnical Society), 2003, 18(3): 92-95. [ 2] 张鹏, 李红斌 (Zhang Peng, Li Hongbin). 一种基于离散小波变换的谐波分析方法(A novel algorithm for Harmonic analysis based on discrete wavelet transforms) [J]. 电工技术学报 (Transactions of China Electrotechnical Society), 2012, 27(3): 252-259. [ 3] 苏玉香, 刘国平, 沈晓群, 等 (Su Yuxiang, Liu Guoping, Shen Xiaoqun, et al.). 改进的Hilbert-Huang变换在船舶电网谐波检测中的应用 (Improved Hilbert-Huang trans-form applied in power quality detection in marine power system) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2011, 30(3): 10-14. [ 4] 杨玉坤, 杨明玉 (Yang Yukun, Yang Mingyu). Prony算法在谐波、间谐波参数辨识中的应用 (Application of Prony algorithm in parameter identification of harmonics and inter-harmonics) [J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2012, 24(3): 121-126. [ 5] 张惠娟, 汪友华, 王艳延, 等 (Zhang Huijuan, Wang Youhua, Wang Yanyan, et al.). 基于AR模型的电力系统间谐波分析 (Power system interharmonics analysis based on autoregression model) [J]. 电工技术学报 (Transactions of China Electrotechnical Society), 2010, 25(7): 144-149. [ 6] 孟玲玲, 孙常栋, 王晓东 (Meng Lingling, Sun Changdong, Wang Xiaodong). 基于噪声子空间分解MUSIC函数的谐波/间谐波检测算法(Harmonic/inter-harmonic detection based on DNS-MUSIC function) [J]. 电力自动化设备(Electric Power Automation Equipment), 2012, 32(2): 89-94. [ 7] 张静, 徐政, 牛卢璐 (Zhang Jing, Xu Zheng, Niu Lulu). TLS-ESPRIT 在电力系统信号高精度频谱估计中应用(Application of TLS-ESPRIT in high resolution spectrum estimation of power system signal) [J]. 电力自动化设备(Electric Power Automation Equipment), 2009, 29(5): 48-51. (,cont.onp.37)(,cont.fromp.12) [ 8] 张宇辉, 段伟润, 李天云 (Zhang Yuhui, Duan Weirun, Li Tianyun). 基于多级EEMD和WVD分布的谐波/间谐波检测方法(Method to detect harmonics and inter-harmonics based on multiple-level EEMD and Wigner-Ville distribution) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2015, 34(3): 66-71. [ 9] 侯世英, 张文玉, 孙韬, 等 (Hou Shiying, Zhang Wenyu, Sun Tao, et al.). 基于正交优化时频原子分解算法的电能质量扰动匹配特征分析 (Analysis on matching features of power quality disturbances based on orthogonal optimization of time-frequency atom decomposition) [J]. 电网技术(Power System Technology), 2013, 37(3): 647-652. [10] 李明, 张葛祥, 王晓茹 (Li Ming, Zhang Gexiang, Wang Xiaoru). 时频原子方法在间谐波分析中的应用(Application of time-frequency atom method in inter-harmonics analysis) [J]. 电网技术 (Power System Technology), 2009, 33(17): 81-85. [11] 张英杰, 龚庆武, 李勋, 等 (Zhang Yingjie, Gong Qingwu, Li Xun, et al.). 基于 PSO 的原子分解法在间谐波分析中的应用 (Application of atomic decomposition based on PSO in inter-harmonics analysis) [J]. 电力系统保护与控制 (Power System Protection and Control), 2013, 41(15): 41-48. [12] Mallat S G, Zhang Z F. Matching pursuits with time-frequency dictionaries [J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415. [13] 卢泽华, 罗日成, 黄彪, 等 (Lu Zehua, Luo Richeng, Huang Biao, et al.). 协同进化蜜蜂算法结合谱估计的间谐波参数分析 (Analysis of inter-harmonics parameters using co-evolutionary bees algorithm and spectral estimate) [J]. 中南大学学报 (Journal of Central South University), 2014, 45(8): 2654-2660. [14] Leonowicz Z, Lobos T, Rezmer J. Advanced spectrum estimation methods for signal analysis in power electronics [J]. IEEE Transactions on Industrial Electronics, 2003, 50(3): 514-519. Harmonic and inter-harmonic detection based on FFT and optimized matching pursuit CHEN Lei1, 2, ZHENG De-zhong1, ZHAO Xing-tao1, LIAO Wen-zhe3 (1. Key Laboratory of Measurement Technology and Instrumentation of Hebei Province, Yanshan University, Qinhuangdao 066004, China; 2. Northeast Petroleum University at Qinhuangdao, Qinhuangdao 066004, China; 3. School of Control Science and Engineering, Hebei University of Technology, Tianjin 300130, China) Harmonic and inter-harmonic disturbances seriously affect the normal operation of power system, and a FFT and local optimized matching pursuit (MP) based on sinusoid dictionary method is used to detect the waveform parameters in case of noise, fundamental frequency deviation and similar inter-harmonic frequency with harmonic or fundamental frequency. According to the amount of energy, the harmonic and inter-harmonic disturbances are extracted in turn through iteration. During each iteration, firstly,FFT is used to estimate the current frequency parameter, and then the phase is searched under this frequency; further, the Nelder-Mead algorithm is used to acquire the optimized frequency and phase that exact matches with the disturbance. Finally, the signal expression matching with harmonic or inter-harmonic is gained by MP, and the amplitude is acquired. The simulation results show that the proposed approach has good detection precision and anti-noise performance. harmonic; inter-harmonic; matching pursuit; sinusoid dictionary; time-frequency atom; optimal computation 2015-05-28 河北省自然科学基金(F2014203224)、秦皇岛市科学技术研究与发展计划 (201302A042)资助项目 陈 雷 (1979-), 男, 辽宁籍, 副教授, 博士研究生, 研究方向为电能质量分析、智能检测与信号处理; 郑德忠 (1949-), 男, 吉林籍, 教授, 博士生导师, 研究方向为系统仿真、信号处理等。 TM935 A 1003-3076(2016)02-0007-063 基于优化MP的谐波间谐波检测
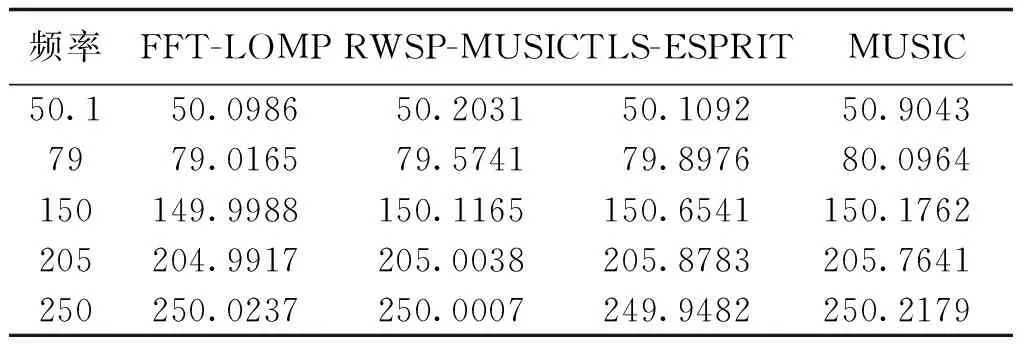
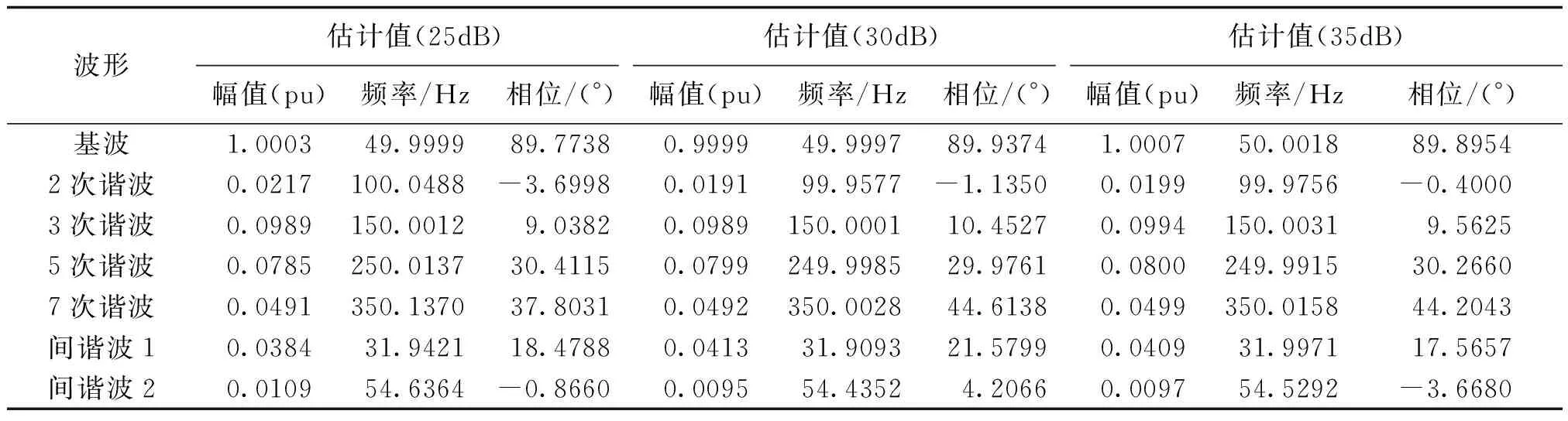
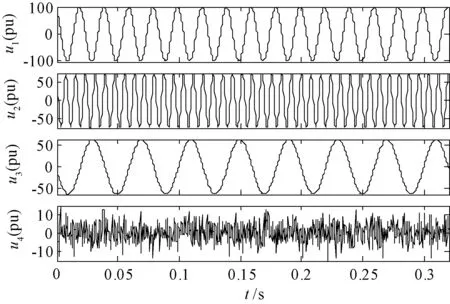
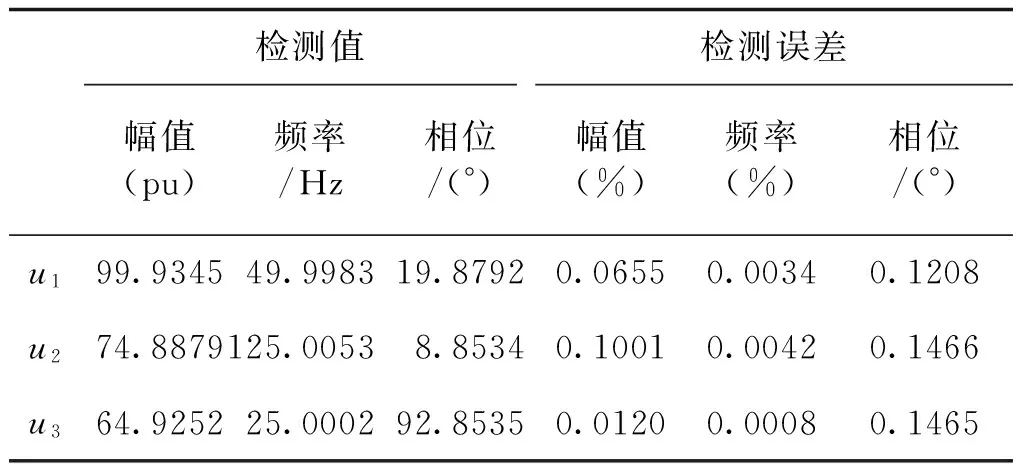
4 算例分析





5 结论
