撑游戏之篙,让数学课堂有趣又有效
2016-05-25江苏扬州市江都区真武镇滨湖小学225268沈延安
江苏扬州市江都区真武镇滨湖小学(225268)沈延安
撑游戏之篙,让数学课堂有趣又有效
江苏扬州市江都区真武镇滨湖小学(225268)沈延安
[摘要]在小学数学教学中,游戏作为一种学生喜闻乐见的教学形式,得到了广泛的课堂应用。如何将知识和游戏巧妙结合,寓教于乐,这是每一个数学教师都要面对并为之思考的重要课题。
[关键词]游戏教学小学数学教学策略思维发展
小学生的思维主要是从形象思维逐步过渡为抽象思维,这种思维的转化,没有想象的展开是不可能实现的。心理学和教育学指出,数学游戏是促进学生认知内化的重要途径之一,能够为思维的创造性、流畅性和灵活性奠定基础。那么,如何将数学游戏有效应用在课堂教学中呢?
一、创设游戏情境,激发求知兴趣
课程标准明确指出,数学教学的本质是要能够调动学生的积极性,激发求知兴趣,引发学生的思考,因此,课堂情境的营造具有重要的作用。在教学中,教师应积极设置游戏悬念,激发学生的探究欲望,带领学生迅速进入课堂情境,展开数学探究。
例如,在教学苏教版“公倍数与最小公倍数”时,我创设了这样的游戏情境:出示一个正六边形和一个正方形(如图1),两张图片拼起来是一只可爱的猴子,现在固定正六边形不动,将正方形沿着正六边形向一个方向转动,我们看看将会发生什么变化?学生被这样的教学悬念调动起来,很快发现了一个有趣的现象:当正方形开始转动时,猴子的尾巴断了。此时我追问:如何才能将猴子的尾巴重新接回呢?需要转动几次?这个悬念设置激发了学生强烈的探究欲望,学生大胆猜测,有的认为是6次,有的认为是12次,还有的认为是22次,到底哪个才对呢?于是,学生展开验证,转6次,尾巴没有接回,转到12次时尾巴又接回了。到底是怎么回事?有什么规律呢?学生的好奇心一触即发。
教师通过创设游戏情境,让课堂充满悬念和趣味,为学生探究真知提供了动力,也奠定了良好的心理基础。

图1
二、设计游戏操作,形成直觉感知
教育家阿莫纳什维利认为,学生获得知识的最有效途径是动手操作。只有从直接的操作中,才能获得最直观真切的个人直觉经验,从而激活数学思维,使之得到思维的提升和发展。在教学中,教师可以借助游戏操作,将复杂的数学问题简明化、形象化。
例如,在教学苏教版“公倍数与最小公倍数”时,第一次游戏(正六边形+正方形)是我进行演示的,但对于学生来说,只有动手操作才能加深直观认知。为此我设计了动手操作游戏:出示大屏幕,让学生看看图形是几边形和几边形(如图2),想一想需要转动几次才能将尾巴重新接回。学生以小组为单位,先进行猜想,然后进行实践操作,并将得到的数据进行比较和验证。此时我问学生:和第一次游戏相比,这次游戏中什么条件变了?什么没变?学生的注意力被引向数学思考。学生认为,从多边形边数看,第一次游戏中6和4不互质,第二次游戏中8和5互质;从接回次数看,第一次的数值比较小,第二次比较大。通过比较和思考,学生对这个游戏有了直观认知,揭示了游戏背后蕴含的有趣的数学规律。
教师通过学生动手操作游戏,帮助学生形成直觉感知,为学生从不同情况的接回次数中归纳和发现数学规律做好了铺垫。
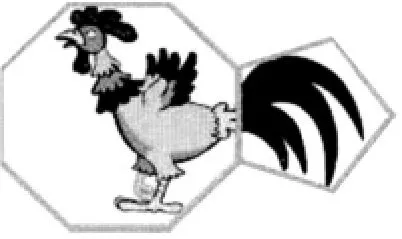
图2
三、发现游戏规律,建构数学模型
教育家斯宾塞指出,教学是从直观开始,以抽象结束。在教学中,建模的过程就是一个数学化的过程,也是学生获得数学建构的过程。教师可以借助游戏活动,帮助学生积累丰富的活动经验,引导发现游戏规律,进行必要的数学抽象,建构数学模型。
例如,在教学苏教版“公倍数与最小公倍数”时,我让学生总结两次尾巴重新接回的游戏,看看发现了什么规律。有学生认为,两个图形边数相乘就能得到尾巴重新接回的次数,比如4乘6等于24,则24就是尾巴重新接回次数中的一个。也有学生认为,虽然两个图形的边数相乘能够得到一个重新接回的次数,但还不完整。比如,12、36都是能重新接回的次数,它们既是6的倍数又是4的倍数。此时我追问:“尾巴接回的奥秘是什么?”学生最终发现,接回次数就是两个正多边形边数的公倍数,而第一次接回的次数就是它们的最小公倍数!
教师引导学生对游戏活动进行反思和总结,从而发现规律,获得了程序性的知识,有效建构了最小公倍数的数学模型。
总之,将游戏运用在小学数学教学中,能够有效激发学生的兴趣,催化学生的数学思维,激活直观感知,从而建构数学模型,实现数学课堂的趣味性和有效性。
(责编李琪琦)
[中图分类号]G623.5
[文献标识码]A
[文章编号]1007-9068(2016)11-052
