给定阶子群的-次正规性对群结构的影响
2016-05-25高百俊
高百俊,张 佳,缪 龙
(1. 扬州大学数学科学学院,江苏 扬州 225002;2. 伊犁师范学院数学与统计学院,新疆 伊宁 835000)

高百俊1,2,张 佳1,缪 龙1
(1. 扬州大学数学科学学院,江苏 扬州 225002;2. 伊犁师范学院数学与统计学院,新疆 伊宁 835000)



文中所涉及的群均为有限群,所用术语与符号都是标准的,见文[8-9]。
1 预备知识
为方便起见,我们首先列出在后面的证明中将会用到的一些定义和结果。


引理2[9]设G是有限群,p是|G|的极小素因子。设H是群G的一个子群且|G∶H|=p,则H正规于G。
引理3[10]设G是有限群,则

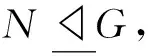

引理4[8]设N是群G的可解正规子群且N≠1。若N∩Φ(G)=1,则N的Fitting子群F(N)是G的包含于N中的所极小正规子群的直积。

(iv) 对于P的任意极大子群P1,P∩B=P1∩B=Φ(P)∩B且|G∶P1B|=p。
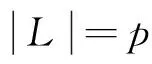
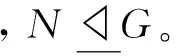
引理7[12]如果G是一个p-超可解群且Op′(G)=1,那么G是超可解的。
2 主要结果

证明 必要性显然。下面主要证明充分性。
(vi) 若|D|=|P|,则由引理1可知结论正确。
(vii) 若|D|=p,假设结论不真,设G为极小阶反例。

故当|D|=p时,结论成立。
(viii) 若p<|D|<|P|,假设结论不真,设G为极小阶反例。

综合(vi)-(viii)可知定理1得证。

证明 必要性显然。下面主要证明充分性。
假设结论不真,设G为极小阶反例。
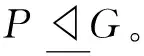



证明 假设结论不真,设G为极小阶反例。


证明 假设结论不真,设G为极小阶反例。
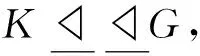

证明 若|D|=|P|,则由定理3可知结论成立。
若|D|=p,则由定理4可知结论成立。
考虑p<|D|<|P|,假设结论不真,设G为极小阶反例。
(xi)Op′(G)=1。
事实上,若Op′(G)≠1,考虑商群G/Op′(G),则由引理3(iii)知G/Op′(G)满足定理条件,由G的选择知G/Op′(G)是p-超可解的,因此G是p-超可解的,矛盾。
(xii)Op(G)≠1。

(xiii)Op(G)∩Φ(G)=1。

(xiv) 最后的矛盾。

[1] 黄裕建, 李样明.p-幂零群的一个等价条件[J]. 中山大学学报(自然科学版), 2008, 47(5): 14-17.
[2] 郭桂容, 赵涛. 弱S-嵌入子群与有限群的超可解[J]. 中山大学学报(自然科学版), 2013, 52(4): 25-28.
[3] 何宣丽, 李样明, 王燕鸣. 含有C*-正规子群的有限群[J]. 中山大学学报(自然科学版), 2009, 48(5): 12-15, 23.


[6]LIXH,ZHAOT.SΦ-supplementedsubgroupsoffinitegroups[J].UkrainianMathJ, 2012, 64: 92-99.
[7]LIJB,XIEFY.Oninequalitiesofsubgroupsandthestructureoffinitegroups[J].JInequalAppl, 2013, 2013(1): 427-433.
[8] 郭文彬. 群类论[M]. 北京: 科学出版社, 1997.
[9] 徐明曜. 有限群导引(上) [M]. 北京:科学出版社, 2007.

[11] 徐明曜, 黄建华, 李慧陵,等. 有限群导引(下)[M]. 北京:科学出版社, 1999.
[12]GUOW,SHUMKP,SKIBAAN.Criterionsofsupersolubilityforproductsofsupersolublegroup[J].PublMathDebrecen, 2006, 68(3/4): 433-449.

GAOBaijun1,2,ZHANGJia1,MIAOLong1
(1.SchoolofMathematicalSciences,YangzhouUniversity,Yangzhou225002,China;2.SchoolofMathematicsandStatistics,YiliNormalUniversity,Yining835000,China)


10.13471/j.cnki.acta.snus.2016.05.005
2016-02-25
国家自然科学基金资助项目(11271016);江苏省研究生创新工程资助项目(KYZZ16_0488)
高百俊(1980年生),女;研究方向:有限群论;E-mail:dqgbj2008@163.com
O
A
0529-6579(2016)05-0027-04
