柔性太阳翼桅杆涂层特性对热诱发振动的影响分析

马泽策，王志瑾，孔祥宏（南京航空航天大学 飞行器先进设计技术国防重点学科实验室，南京 210016）



柔性太阳翼桅杆涂层特性对热诱发振动的影响分析

马泽策，王志瑾，孔祥宏
（南京航空航天大学 飞行器先进设计技术国防重点学科实验室，南京 210016）

摘要：空间站大型柔性太阳翼系统在轨运行期间会受到周期性的热辐射作用，导致结构温度周期性变化，从而诱发太阳翼的振动。为研究太阳翼桅杆热控涂层特性对热诱发振动的影响，文章采用热-结构顺序耦合的方法，对桅杆无涂层、电镀涂层和白漆涂层3种不同表面状态进行热诱发振动分析，得到了太阳翼的位移-时间响应结果。对比不同涂层下太阳翼参考点的振动结果可以看出：涂层特性对于热诱发振动是有影响的，其中白漆涂层能大幅度减小振动的振幅。

关键词：柔性太阳翼；热诱发振动；桅杆；热控涂层；顺序耦合法

http://www.bisee.ac.cnE-mail: htqhjgc@126.comTel:(010)68116407, 68116408, 68116544

0　引言

随着太阳电池材料的革新，大型空间站常采用柔性太阳翼供电。柔性太阳翼具有转换效率高、重量轻、收拢体积小等显著特点。但随着航天器周期性地进出阴影区，冷热交变的高低温环境会导致太阳翼产生结构屈曲、变形，甚至振动。例如，“哈勃”太空望远镜曾经由于太阳翼的热诱发振动问题而不能正常工作，导致传回的图像模糊。

Boley首先提出了热诱发振动问题[1]，并在假设热流不随结构的变形而变化的前提下，研究了梁受突加热载荷引起的振动。在此基础上，研究人员相继发展出对“欧拉-伯努利”梁热-结构耦合[2-3]的补充分析，并拓展到复合材料层合板的振动研究[4-6]。在航天领域，随着航天器太阳翼尺寸的逐渐增大，为了确保其在空间冷热交变环境中安全工作，必须考虑太阳翼结构的热载荷和热诱发振动。目前，主要有热-结构耦合和热-结构非耦合2种理论对柔性太阳翼进行热诱发振动分析[7-8]。在工程实际应用中，又由这2种理论推演出全局耦合而单步非耦合方法[9]和振型叠加法[10]，用来计算复杂太阳翼模型的热诱发振动。

目前国内外的热诱发振动研究，多集中在空间桁架结构或单独柔性阵面的振动，而对太阳翼支撑结构表面涂层对柔性阵面热诱发振动的影响还未见分析。本文基于非耦合热诱发振动的假设，采用顺序耦合的工程算法，对比研究在太阳翼桅杆的3种不同的表面状态下，由热诱发的太阳翼阵面振动情况。

1　顺序耦合的热诱发振动基本原理和分析方法

太阳翼热诱发振动的分析理论通常分为热-结构耦合和非耦合2种。在热载荷不太大时，2种方法的结果非常接近；但当热变形较大时，导致热流入射角度产生较大改变，就需要考虑热-结构的耦合影响[11]。本文研究的太阳翼热变形不大，同时考虑到计算的效率和软件的应用，决定选用非耦合的理论方法。首先采用非耦合热分析计算出太阳翼的热载荷，之后将热载荷加载到振动模型中计算太阳翼的动力学响应。这种计算方法被称为顺序耦合分析法。

1.1非耦合温度场计算

非耦合是进行顺序耦合分析的前提，顺序耦合热诱发振动计算方法的第一步是求解结构随时间变化的温度场。在不考虑热变形的情况下，热传导的微分方程可写为

其辐射的边界条件为

初始条件为

上式中：温度T(x, y, z, t)是位置坐标和时间t的函数；qr(x, y, z, t)为入射热流法向分量；qv为内热源；c为比热容；ρ为密度；k为导热系数；α为太阳吸收比；ε为发射率；σ为斯忒藩-玻耳兹曼常量；T∞为空间温度。

1.2热应力计算的有限元法

弹性体会因温度的变化而产生体积的改变。假设物体受热时只产生线应变，对于各向同性的材料，当温度变化∆T时，则有自由膨胀产生的各方向正应变a∆T，而切应变为0，即

式中：a为热膨胀系数；εx、εy、εz为沿各轴向的应变分量；γxy、γyz、γzx为剪切应变。

使用有限元方法可以计算出各单元各节点由于温度而产生的等效载荷[12]

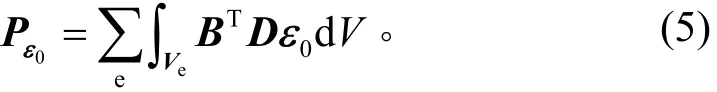
其中：ε0=[a∆Ta∆Ta∆T000]T；B为应变矩阵；D为弹性矩阵；Ve为单元矩阵；V为求解域。

1.3动力学计算的有限元法

动力学有限元方法的求解方程为

其中：M、C、K和F(t)分别为系统的质量矩阵、阻尼矩阵、刚度矩阵和节点外加机械激励力；( t )和( t )分别为节点的加速度和速度。根据有限元热应力理论，热载荷在施加到振动模型中时，实际以等效力的形式作为振动的激励，故将Pε0(t )加入到节点的振动激励中，即

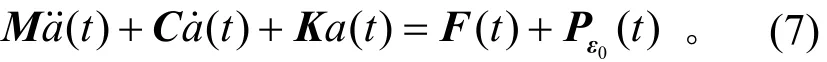
1.4有限元分析方法

根据以上理论，将热诱发振动有限元分析分为2个步骤：

1）根据式(1)～式(3)求解出结构有限元模型各节点的温度载荷，运用有限元软件NX I-deas中的TMG模块来完成这一步骤的计算分析[13]，输出太阳翼桅杆各节点2个周期的温度-时间数据。

2）根据式(4)～式(7)将温度载荷转化为等效激励，得到振动结果。这一步骤的计算分析运用有限元软件Abaqus完成，将时间-温度载荷以预定义场的形式加载到振动模型中的各个节点上，通过隐式动力学分析步计算输出特征点的位移-时间数据。

2　热控涂层对热诱发振动的影响分析

柔性太阳翼的展开与支撑主要依靠桅杆。由于桅杆的刚度比柔性太阳翼电池阵面的刚度大很多，桅杆周期性的热形变会带动阵面发生振动，而桅杆的涂层可以改变其受热状况。下面将运用顺序耦合的方法研究柔性太阳翼的热诱发振动，并通过改变桅杆表面涂层的太阳吸收比和发射率，研究热控涂层对太阳翼热诱发振动的影响。

2.1柔性太阳翼结构及有限元模型简介

柔性太阳翼长约11m，主要结构包括收藏箱体、支撑桅杆和柔性阵面，图1为太阳翼顶端局部有限元模型和桅杆模型。太阳翼共有4个收藏箱体，上下各2个箱体在阵面折叠时作为收藏装置保护阵面，阵面展开时用绳将阵面张紧。可根据收藏箱体的结构特性，将其简化为体单元。2个阵面由位于其中间的桁架式桅杆支撑，桅杆上下端分别与上下收藏箱体相连。由于阵面很薄，可用壳单元来建立其有限元模型。桅杆主要由横框、纵杆和伸缩拉杆组成，初始为收拢状态，后逐节展开伸长。根据横框和纵杆的受力特性，采用梁单元建模，而伸缩拉杆是个二力杆，故将其简化为杆单元。

图1　太阳翼顶端局部有限元模型和桅杆模型Fig. 1　Finite element model of top part of the solar wing and mast

桅杆的两端同上下箱体均与刚度较大的展开锁定装置相连，因而桅杆两端和箱体连接处在有限元模型中均采用刚性约束处理。阵面与箱体之间用绳连接，而绳可使用梁单元建模；绳与箱体通过具有弹簧刚度的张紧机构连接，连接处可视为弹簧元。桅杆与空间站舱体通过抬升机构连接，末端为固支约束。表1为桅杆的部分材料属性。

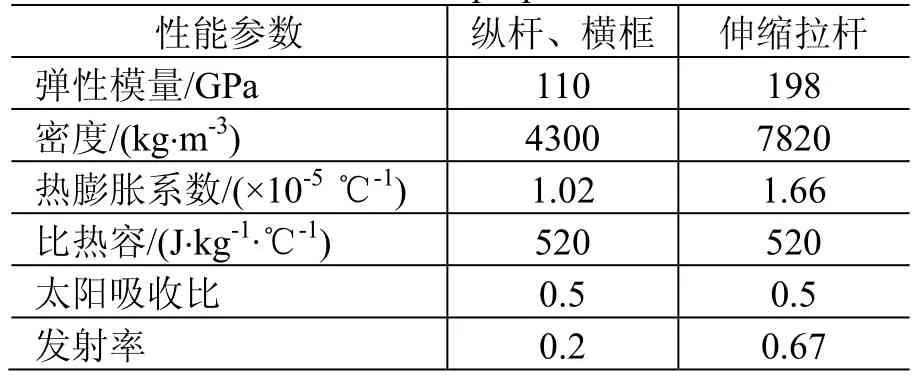
表1　桅杆部分材料属性Table 1　The material properties of the mast

2.2太阳翼温度载荷计算

取0°太阳角惯性飞行作为计算分析工况，计算太阳翼1个轨道周期内的温度载荷。图2为太阳翼柔性阵面和3根无涂层纵杆L1、L2、L3上节点的温度变化曲线。由曲线走势可知，起初温度下降表示太阳翼进入阴影区，然后温度升高至稳定说明飞出阴影区，最后温度再次降低（即再次进入阴影区），如此循环。太阳翼不同部件的材料属性不同，各部件之间还存在相互遮挡，因此各节点的温度-时间曲线是不同的，靠近热流的纵杆L1和L2的温度高于L3的，由此产生的温差则是桅杆发生热变形的主要原因。由于桅杆刚度远大于柔性阵面，桅杆的热变形会带动柔性阵面发生振动，而通过张紧机构的调节可使阵面内的热应力维持在相对稳定的范围。

图2　桅杆和柔性阵面某些点的温度变化Fig. 2　Temperature-time curves for some points of mast and solar cell plate

2.3太阳翼热诱发振动分析

选取太阳翼柔性阵面中部的节点Pm为采样点，输出其沿x轴（桅杆展开方向）、y轴（垂直桅杆方向）和z轴（柔性阵面的法向）3个方向的位移-时间响应。图3～图5为Pm点各轴向的响应曲线，由于两阵面的振动是对称的，故只取其中一个作为分析对象。从图上看出，阵面在x方向基本为准静态响应，y方向有小振幅振动，z方向振幅最大且振动明显。

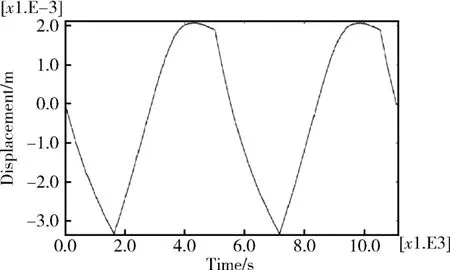
图3　阵面中部节点Pm沿x轴方向位移响应Fig. 3　Displacement response at solar cell plane’s central point Pmalong x-axis

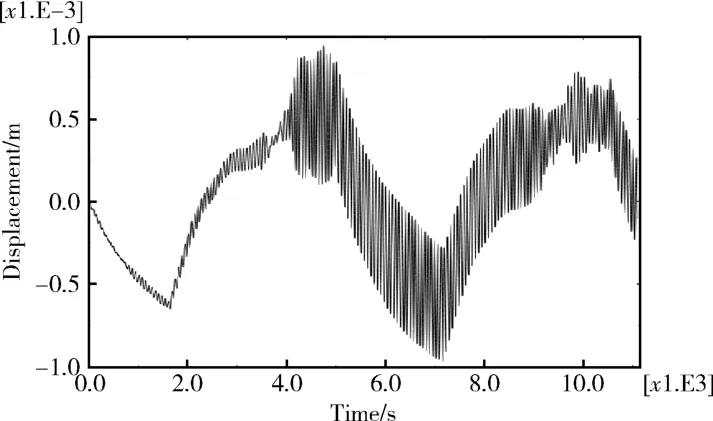
图4　阵面中部节点Pm沿y轴方向位移响应Fig. 4　Displacement response at solar cell plane’s central point Pmalong y-axis

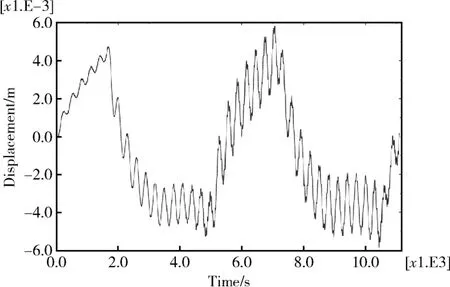
图5　阵面中部节点Pm沿z轴方向位移响应Fig. 5　Displacement response at solar cell plane’s centralpoint Pmalong z-axis

2.4热控涂层对热诱发振动的影响

热控涂层主要改变桅杆的太阳吸收比和发射率，因此在仿真计算过程中只需改变桅杆的这2项属性，其他参数不变。表2为所选热控涂层的参数。

表2　热控涂层特性参数Table 2　Some properties of thermal control coatings

由于阵面x方向为准静态形变，故只对比其他2个方向的热诱发振动响应。图6和图7分别为Pm点在桅杆使用电镀涂层状态下y方向和z方向的振动位移响应与桅杆无涂层状态下的对比曲线。由曲线可知，当桅杆使用电镀涂层时，太阳翼阵面振动的振幅减小。

图6　电镀涂层与无涂层状态下节点Pm在y方向上的位移响应对比Fig. 6　Displacement at Pmalong y-axis by comparing the electrodeposited and non coating cases

图7　电镀涂层与无涂层状态下节点Pm在z方向上的位移响应对比Fig. 7　Displacement at Pmalong z-axis by comparing the electrodeposited and non coating cases

图8和图9分别为Pm点在桅杆使用白漆涂层状态下y方向和z方向的振动位移响应与桅杆无涂层状态下的对比曲线。由曲线可知，当桅杆使用白漆涂层时，太阳翼阵面振动的振幅在y、z两个方向上均大幅减小，在z方向上的缩减尤为明显。

图8　白漆涂层与无涂层状态下节点Pm在y方向上的位移响应对比Fig. 8　Displacement at Pmalong y-axis by comparing the white paint and non coating cases

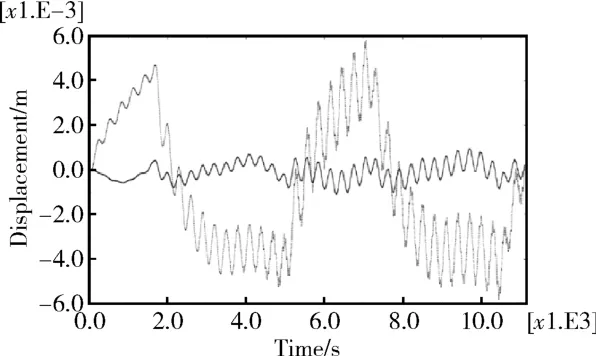
图9　白漆涂层与无涂层状态下节点Pm在z方向上的位移响应对比Fig. 9　Displacement at Pmalong z-axis by comparing the white paint and non coating cases

表3列出了不同桅杆表面状态下，阵面中部节点Pm的最大位移响应结果。根据表3中的数据可以计算出：与无涂层相比，桅杆使用电镀涂层后，阵面最大振幅在y方向减少23.26%，z方向减少18.83%；当桅杆使用白漆涂层后，阵面最大振幅在y方向减小72.18%，z方向减小81.16%。

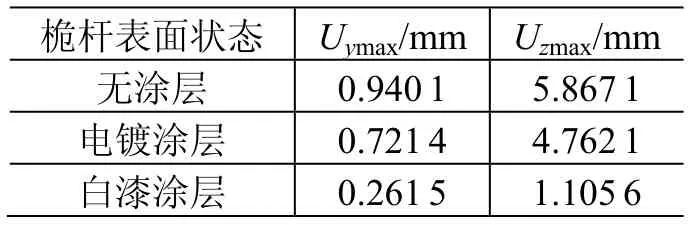
表3　不同桅杆表面状态下的阵面最大位移响应Table 3　Maximum response results of the three coating states

通过观察振动曲线的变化走势还可以看到，在桅杆有热控涂层的状态下，振动曲线的走势更加平缓，而且高频振动的振幅也减小；且白漆涂层状态相对于电镀涂层状态的振幅缩减更加明显。根据式(1)和式(2)可知，涂层的吸收-发射比变小时，可使桅杆温度降低，温度变化幅值减小，因而桅杆不同部位间的温差减小。从能量角度分析，当桅杆吸收的太阳辐射能减少时，意味着给阵面振动提供的能量变少，则阵面的振幅会减小。可见，响应结果比较好地与基本理论吻合。

3　结束语

本文采用顺序耦合的方法，对某航天器柔性太阳翼桅杆在无涂层、电镀涂层和白漆涂层3种表面状态下进行太阳翼柔性阵面热诱发振动比较分析。结果表明，桅杆涂层的改变会影响阵面热诱发振动的幅值，而且涂层的吸收-发射比越小，则振动幅值缩减越明显。因此，在大型柔性太阳翼设计中，需要考虑阵面支撑结构热控涂层对热诱发振动的影响。

本文采用的有限元分析方法不考虑热-结构的耦合问题，将热分析和振动分析分开进行仿真计算。这种方法简化了分析的流程、提高了效率，可对整个太阳翼进行仿真计算；但为提高精度，后续应进一步探求耦合假设下的仿真计算方法。

参考文献(References)

[1] Boley B A. Thermally induced vibrations of beams[J]. Journal of the Aeronautical Science, 1956, 23(2): 179-181

[2] Seibert A G, Rice J S. Coupled thermally induced vibrations of beams[J]. AIAA Journal, 1973, 11(7): 1033-1035

[3] Shen Z, Tian Q, Liu X, et al. Thermally induced vibrations of flexible beams using absolute nodal coordinate formulation[J]. Aerospace Science and Technology, 2013, 29(1): 386-393

[4] Tran T Q N, Lee H P, Lim S P. Structural intensity analysis of thin laminated composite plates subjected to thermally induced vibration[J]. Composite Structures, 2007, 78(1): 70-83

[5] Panda S K, Sing B N. Nonlinear finite element analysis of thermal post-bucking vibration of laminated composite shell panel embedded with SMA fibre[J]. Aerospace Science and Technology, 2013, 29(1): 47-57

[6] 孙良新, 范绪箕. 热载荷作用下层合板瞬态响应分析[J].振动工程学报, 1989, 2(4): 12-22 Sun Liangxin, Fan Xuji. Transient response analysis of laminated composite plate subjected to suddenly applied heating[J]. Journal of Vibration Engineering, 1989, 2(4): 12-22

[7] Thornton E A, Kim Y A. Thermally induced bending vibrations of a flexible rolled-up solar array[J]. Journal of Spacecraft and Rockets, 1993, 30(4): 438-448

[8] 王焘, 冯刚, 张铎, 等. 柔性太阳电池阵的热-结构耦合分析[J]. 空间科学学报, 2002, 22(2): 50-54 Wang Tao, Feng Gang, Zhang Duo, et al. Analysis of heat-structure coupling on flexible solar cell series[J]. Chinese Journal of Space Science, 2002, 22(2): 50-54

[9] 安翔, 冯刚. 某空间站太阳电池阵中央桁架热-结构耦合动力学分析[J]. 强度与环境, 2005, 32(3): 8-13 An Xiang, Feng Gang. Thermally induced vibration of the main mast of the space station’s solar arrays[J]. Structure & Environment Engineering, 2005, 32(3): 8-13

[10] 姚海民, 薛明德, 丁勇. 大型空间结构热诱发振动的有限元分析[J]. 清华大学学报: 自然科学版, 2002, 42(11): 1524-1527 Yao Haimin, Xue Mingde, Ding Yong. Thermally induced vibration analysis of large space structures using the finite element method[J]. Journal of Tsinghua Univercity: Sci & Tech, 2002, 42(11): 1524-1527

[11] Zhang J, Xiang Z, Liu Y, et al. Stability of thermally induced vibration of a beam subjected to solar heating[J]. AIAA Journal, 2014, 52(3): 660-665

[12] 王勖成. 有限单元法基本原理和数值方法[M]. 2版.北京: 清华大学出版社, 1997

[13] 黄后学, 刘振宇, 陈娅琪, 等. 不同工况下空间太阳电池翼的在轨热分析[J]. 上海交通大学学报, 2012, 46(5): 790-795 Huang Houxue, Liu Zhenyu, Chen Yaqi, et al. Thermal analysis of solar panels in orbit under different operating conditions[J]. Journal of Shanghai Jiaotong University, 2012, 46(5): 790-795

（编辑：肖福根）

Influence of mast’s coating of the flexible solar wing on thermally induced vibration

Ma Zece, Wang Zhijin, Kong Xianghong
(Ministerial Key Discipline Laboratory of Advanced Design Technology of Aircraft, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Abstract:On the orbit, a large flexible solar wing system of the space station would suffer a periodic thermal radiation and therefore a structural vibration. In order to investigate the influence of the mast’s thermal control coating on the vibration, a sequential coupled thermal-structural analysis method is used to calculate the thermally induced vibration. For three different states of the mast’s surface, that is, without coating, with electrodeposited coating and and with white paint coating, the displacement vs. time response is calculated correspondingly. The results show that the thermal control coating indeed has an influence on the thermally induced vibration, and the greatest mitigation effect is found for the case with the white paint coating.

Key words:flexible solar wing; thermally induced vibration; mast; thermal control coating; sequential couple method

作者简介：马泽策（1991—），男，硕士研究生，主要研究方向为飞行器结构设计。E-mail: mazece@163.com。

基金项目：江苏高校优势学科建设工程资助项目

收稿日期：2015-08-26；修回日期：2016-03-10

DOI:10.3969/j.issn.1673-1379.2016.02.006

中图分类号：V415.4

文献标志码：A

文章编号：1673-1379(2016)02-0149-05