两种改进的变步长MPPT算法性能对比研究

潘逸菎, 窦 伟

(北京科诺伟业科技股份有限公司， 北京 100083)

两种改进的变步长MPPT算法性能对比研究

潘逸菎, 窦 伟

(北京科诺伟业科技股份有限公司， 北京 100083)

光伏阵列最大功率点跟踪(MPPT)技术是光伏发电应用的关键技术之一。本文基于近年来学界研究成果，对实际应用最多的变步长电导增量法和扰动观察法两种MPPT技术进行优化设计，并详细对比验证了两种改进方法特性。对比仿真和实验结果表明，改进算法均能快速准确地实现最大功率跟踪，其中改进的扰动观察法因算法简单更适合实际产品使用。

MPPT； 光伏并网逆变器； 电导增量法； 扰动观察法

1 引言

光伏电池可将太阳能转化为电能，但其输出电压和电流会随着光照强度和环境温度的变化而表现出较强的非线性，为使光伏电池输出功率始终保持在最大值附近，光伏阵列最大功率点跟踪(maximum power point tracking，MPPT)技术已成为光伏发电系统中的重要研究内容。

目前，常用的MPPT方法包括：恒定电压法、扰动观察法[1]、电导增量法[2]、滞环比较法[3]、模糊控制[4]和神经网络[5]等。其中恒定电压法所依据参数与外界环境相关，跟踪效果不理想。神经网络法跟踪效果较好，但样本获取过程较难且不易达到预期效果。模糊控制法能快速响应外部环境变化，但需以“专家经验”做为基础，而实际“专家经验”并不完备，故存在局限性。当前，实际应用中大多采用扰动观察法和电导增量法。扰动观察法由于原理简单、易于实现而成为MPPT控制中应用和研究最为广泛的方法之一。而电导增量法具备控制精度高、稳定性好等优点，且与光伏电池输出特性及参数无关。

本文以目前实际产品应用最多的电导增量法和扰动观察法为研究目标，对两种算法分别进行了优化分析，并通过仿真与实验对两种方法的动、静态性能进行了比较。

2 光伏电池阵列数学模型

本文采用的光伏阵列数学模型如下[6]。

在环境温度为Ta时，光伏电池温度Tc为：

Tc=Ta+tcR

(1)

式中，R为光伏阵列倾斜面上的总太阳辐射；tc为太阳电池模块的温度系数。

设在参考条件下，Isc为短路电流，Voc为开路电压，Im和Vm分别为最大功率点(MPP)电流和电压，那么当光伏阵列电压为V、且考虑太阳辐射变化和温度影响时，对应组件电流I为：

(2)

(3)

(4)

(5)

(6)

(7)

式中，Rref和Tref分别为太阳辐射和光伏电池温度的参考值；α和β分别为参考日照强度时电流和电压温度系数；Rs为光伏模块内阻。

最大功率点对应最大输出电流Im和最大输出电压Um。通过调节直流母线电压，控制外电路阻值与光伏电池内阻匹配，从而使光伏电池工作在最大功率点。光照、温度等环境因素变化时，光伏组件最大功率点位置会发生偏移。图1为设定环境温度分别为25℃和45℃不变、不同光照强度下光伏组件的输出I-U和P-U曲线。其中，曲线1、曲线3、曲线5光照强度分别为1200W/m2、1000W/m2、800W/m2，温度为25℃。曲线2、曲线4、曲线6光照强度分别为1200W/m2、1000W/m2、800W/m2，温度为45℃。

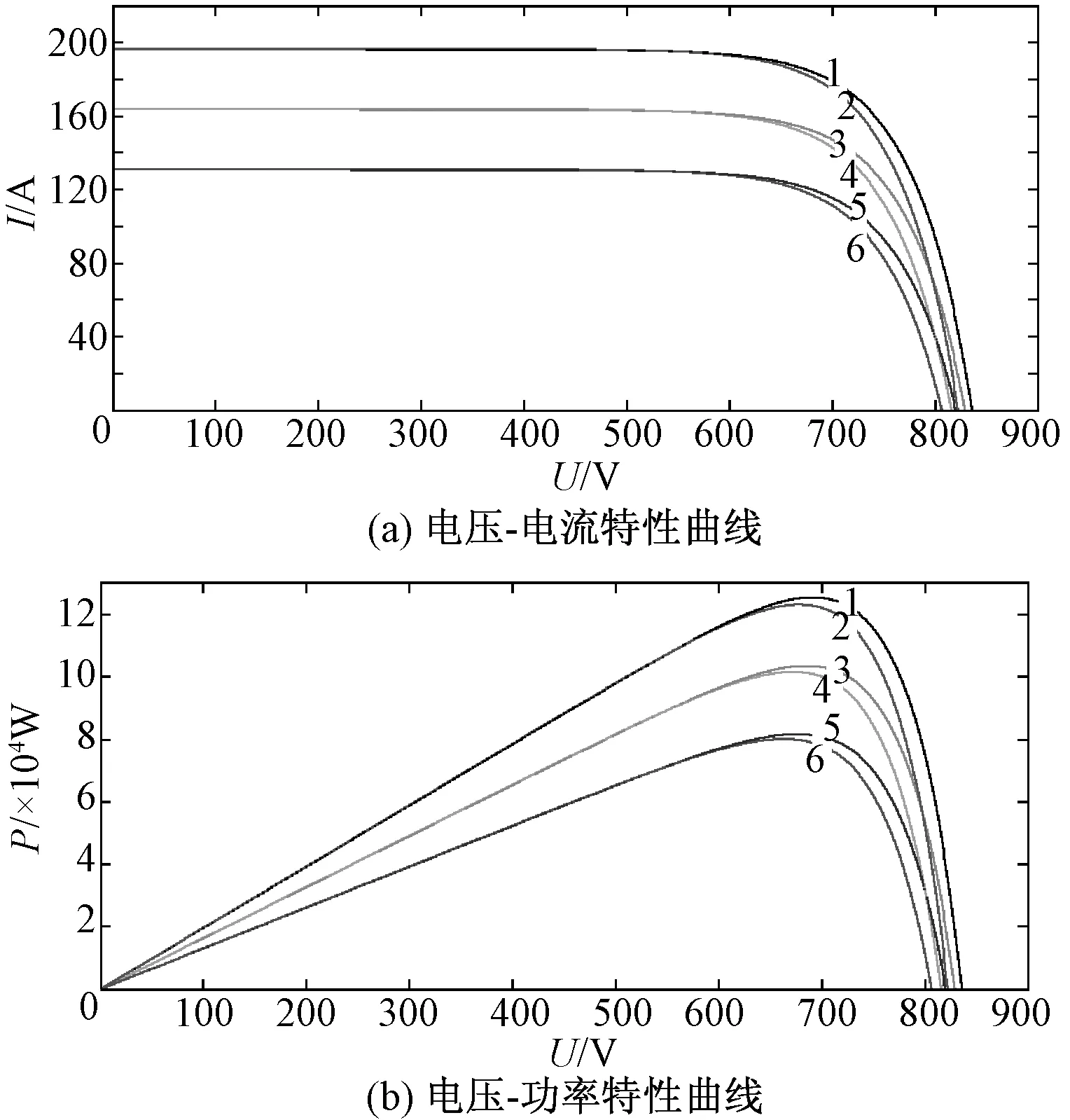
图1 不同温度及光照强度光伏电池输出特性Fig.1 Output characteristics of PV cell under different temperatures and illumination intensities

由图1可知，同一温度下，光伏特性曲线随光照强度的增加，最大功率点向上偏移，短路电流随着光照强度的升高而增大，而开路电压随着光照强度的升高略有增大。同一光照强度下，光伏特性曲线随温度的增加，最大功率点向下偏移，开路电压向左偏移，即温度对开路电压有明显的影响。而特性曲线在恒流源线性区域受温度影响变化不大，温度升高时短路电流Isc几乎不变。

3 改进型MPPT算法原理分析

3.1 改进型电导增量法

对于定步长电导增量法，步长大小决定了系统的跟踪速度。选用较大的扰动步长可提高跟踪速度，但到达最大功率点附近时波动较大，稳态功率损失较多；较小的扰动步长可提高稳态跟踪精度，但跟踪速度较慢。

变步长电导增量法[7]是目前实际应用的一种优化算法,其示意图如图2所示。传统变步长算法依靠光伏电池功率-电压微分(dP/dU)来调整步长，但由图2可知，不同光照强度下|dP/dU|曲线差异较大，无法找到一个最优的速度因子来满足光照剧烈变化条件下的最大功率点跟踪需求。

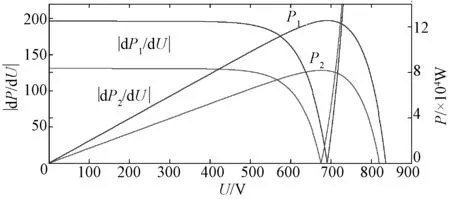
图2 变步长电导增量法示意图Fig.2 Diagram of variable step-size incremental conductance algorithm

根据光伏电池输出特性可得：

(8)

式(8)表明dP/dU与光伏电池的输出电流密切相关，而当外界环境变化时光伏电池的输出特性变化较大。为削弱外界变化的影响，设步长调整系数S的表达式为：

(9)

式中，S(k)为k时刻S取值；U(k)和I(k)分别为k时刻的电压值和电流值。

不同光照强度下步长调整系数S(k)的变化曲线如图3所示。图3中，步长调整系数S在远离最大功率点的左侧区域取值近似为1，当系统工作点越靠近最大功率点时步长调整系数越小，并在最大功率点处变为0，且不同光照强度下步长调整系数S的变化趋势和取值范围基本一致。此外，步长调整系数S曲线相比于dP/dU曲线更加平滑，故更适于调整MPPT控制算法步长。

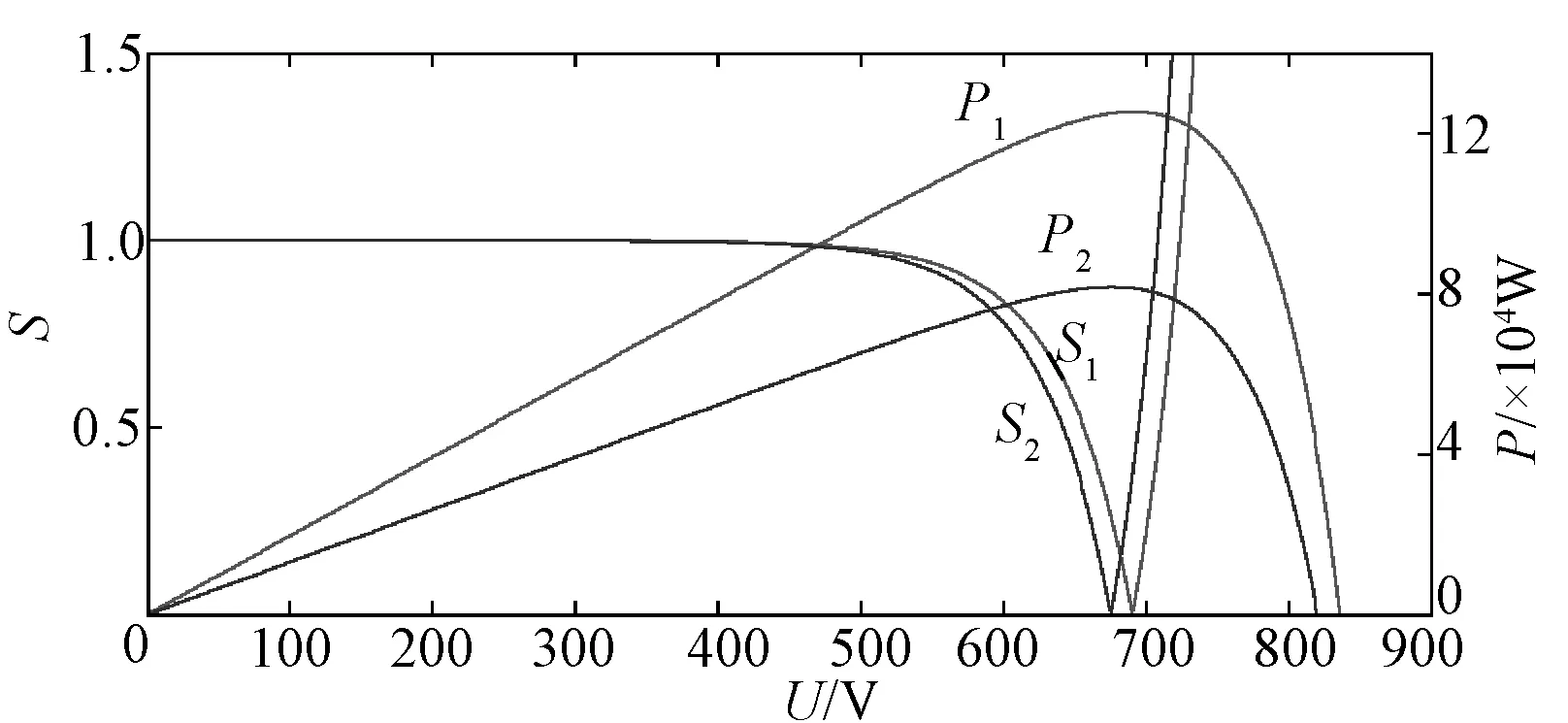
图3 改进型变步长电导增量法示意图Fig.3 Diagram of modified variable step-size incremental conductance algorithm

改进型变步长电导增量法的步长更新规则为：

(10)

式中，ΔUref为扰动定步长；Uref(k-1)和Uref(k)分别为k-1时刻和k时刻的参考电压值。

为了保证算法在最大功率点右侧的收敛性，令S(k)≤1。改进型电导增量法流程图如图4所示。图4中，采用传统电导增量法判断光伏系统工作点的位置。G(k)与式(8)符号一致，当工作点位于最大功率点右侧且S(k)>1时，系统工作于步长为ΔUref的定步长模式，即取S(k)=1；否则，系统工作在变步长模式，步长为S(k)ΔUref。

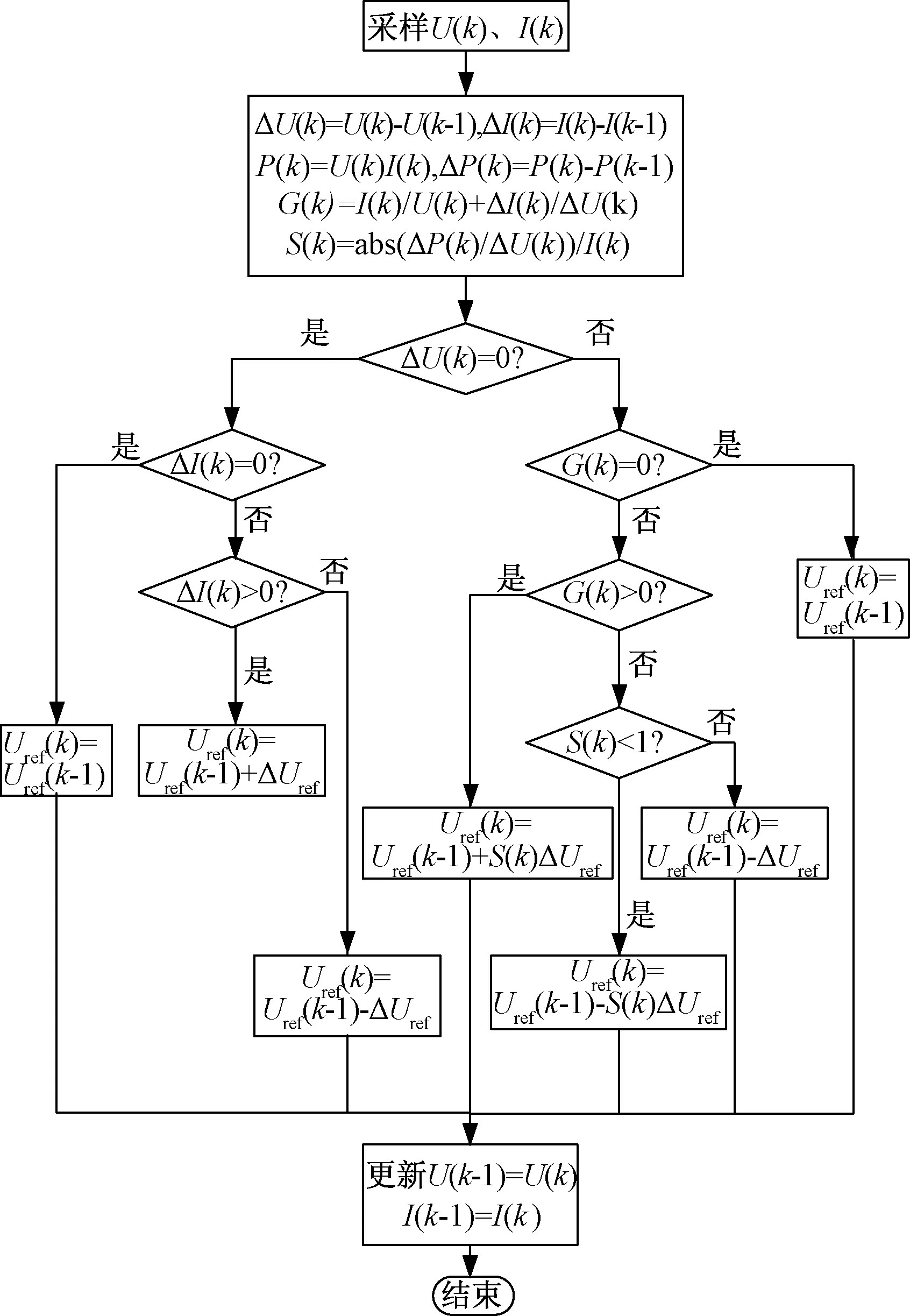
图4 改进型变步长电导增量法流程图Fig.4 Flowchart of improved variable step length incremental conductance algorithm

3.2 改进型扰动观察法

扰动观察法(P&O)工作原理为周期性地在光伏电池的输出电压上施加一定的扰动ΔV，观察扰动前后输出功率的变化ΔP，如果ΔP为正，则光伏电池工作点位于最大功率点左侧，方向不变继续施加扰动；如果ΔP为负，则光伏电池工作点位于最大功率点右侧，需改变扰动方向，使光伏电池工作点不断靠近最大功率点。与电导增量法类似，扰动观察法采用定步长策略时，存在高动态性能与高稳态精度同时获取的矛盾，故本文提出一种改进型扰动观察法替代传统定步长方法，满足两种性能的需要。

光伏电池输出特性P(U)为一非线性函数，且连续一次可导，根据该特性，参考电压的变步长扰动表达式为：

(11)

式中，a为一非负常数，即变步长速度因子。a值可由式(12)估算：

(12)

式中，Ustep_max是P&O法的允许最大步长。光伏阵列定标后的I-U、P-U和abs(dP/dU)-U曲线如图5所示，可以看出，|dP/dU|max对应电压值接近于开路电压Uoc，可由式(13)估算：

(13)

式中，n为一个接近1的正数。a可由式(12)和式(13)计算取值范围，并最后通过具体的仿真校验取值。

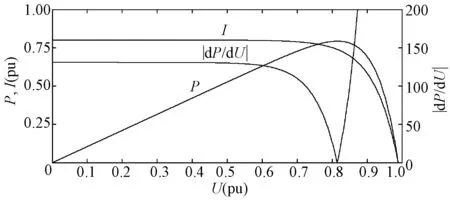
图5 光伏阵列定标后的I-U、P-U和abs(dP/dU)-U曲线Fig.5 Empirical calibration curves of I-U, P-U and abs(dP/dU)-U of PV array

该算法执行流程为：首先，以恒电压控制方式启动，在电压达到固定电压U0前，保持参考电压Uref不变；之后，用变步长代替传统P&O算法的固定步长，当工作点位于MPP左侧时，Uref以一较大的幅度增加，靠近MPP时，自动减小步长；反之当工作点位于MPP右侧时，Uref以一较大的幅度减少，当工作点位于MPP附近时，由于此时斜率较小，则提供一个较小的扰动量，可改善MPP附近振荡情况，从而使系统具有更优越的动态和稳态性能。最后，设定输出功率变化量门槛值ε，在达到MPP附近时，若输出功率变化量|ΔP|小于ε，则视此点为MPP，停止扰动，以固定电压方式运行。该方法对MPP处的稳态特性进行优化，可有效减小光伏阵列输出功率在MPP的振荡现象，反之则继续扰动，即可使输出电压尽快稳定在MPP附近。改进型扰动观察法的MPPT流程如图6所示。

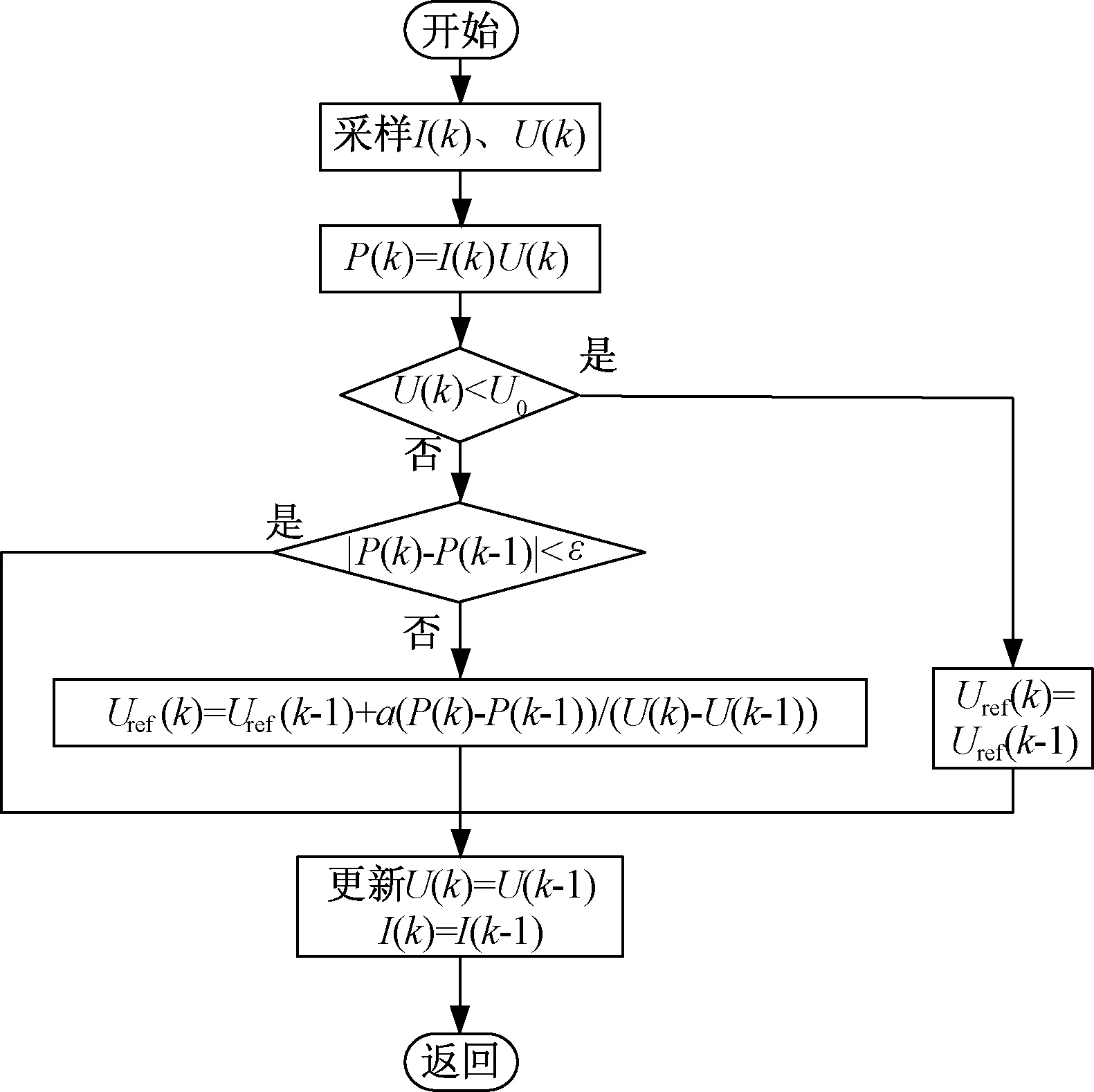
图6 改进型P&O法流程图Fig.6 Flowchart of P&O algorithm

4 仿真对比与实验

根据光伏组件模型及控制策略，在Matlab/Simulink环境下搭建了光伏逆变并网仿真模型。将第3节的两种MPPT方法分别进行了仿真并计算出效率值。

4.1 MPPT效率计算方法

静态MPPT效率表征稳态时MPPT靠近及保持在MPP运行的能力，表达式如下[8]：

(14)

式中，PPV(t)为组件输出实际功率；PMPP(t)为组件理论最大功率。

离散仿真时，可得对应各采样时刻(k时刻)的静态效率表达式：

(15)

为减小离散采样过程产生的随机误差，通常取稳态时多采样点效率平均值为ηstatic，即

(16)

采集两种MPPT方法仿真波形中不同光照条件时静态功率点，代入式(16)可得相应的静态MPPT效率。

动态MPPT效率表征光强或温度变化导致的动态过程中系统跟踪MPP的能力，已知动态过程光伏组件输出功率PPV(t)瞬时值及组件理论最大功率PMPP(t)瞬时值时，动态MPPT效率公式如下所示[9]：

(17)

式中，T0为动态周期。

仿真为基于采样时间Ts的离散计算时，动态MPPT效率公式可转化为：

(18)

采集两种MPPT方法仿真波形中光照强度变化后的动态功率点，代入式(18)可得相应的动态MPPT效率。

4.2 MPPT仿真结果及分析

本文所搭建仿真模型，默认设置环境温度为25℃。并且每次仿真前20s非稳态波形均不在效率的计算范围内。在仿真波形中，Um为最大功率点电压，Udc为实际直流电压，P为实际光伏组件功率。

图7为改进型变步长电导增量法仿真波形图。如图7(a)所示，当光照强度保持在1000W/m2时，参考电压和输出功率的波形，经过计算，在仿真的10min内发电量为17.3315 kW·h，其静态MPPT效率为99.97%。如图7(b)所示，当光照强度在1000～300W/m2之间变化时，参考电压和输出功率的波形，计算后得出10min内发电量为10.9925 kW·h，在这10min内的平均MPPT动态效率为99.90%。

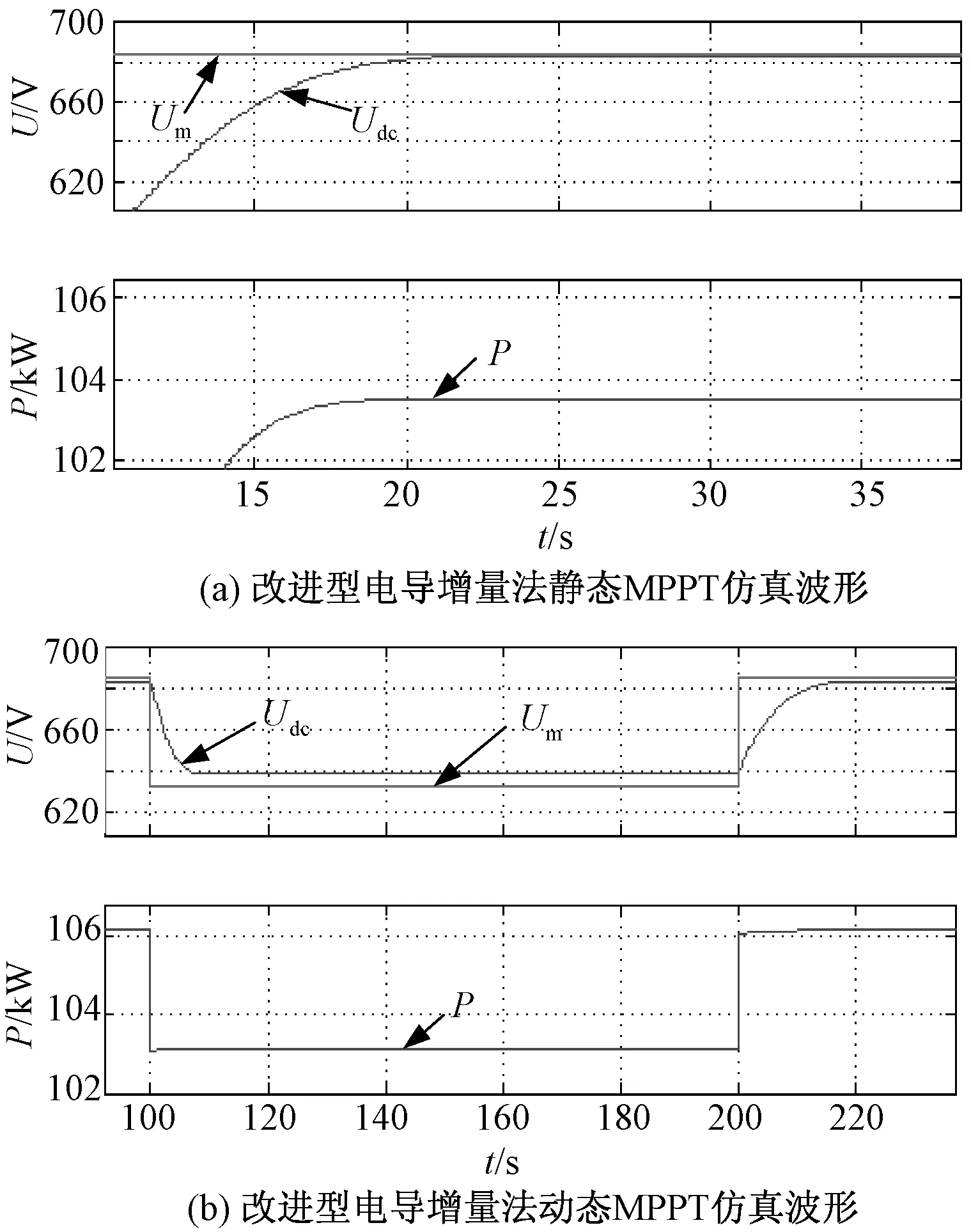
图7 改进型电导增量法MPPT仿真波形图Fig.7 Dynamic MPPT simulation waveforms of improved variable step length incremental conductance algorithm

图8为改进型扰动观察法仿真波形图。如图8(a)所示，当光照强度保持在1000W/m2时，参考电压和输出功率的波形，经计算，在仿真的10min内发电量为17.3332 kW·h，其静态MPPT效率为99.98%。如图8(b)所示，当光照强度在1000～300W/m2之间变化时，参考电压和输出功率的波形也具有较好的跟踪效果。计算后得出10min内发电量为10.9986 kW·h，在这10min内的平均MPPT动态效率为99.96%。

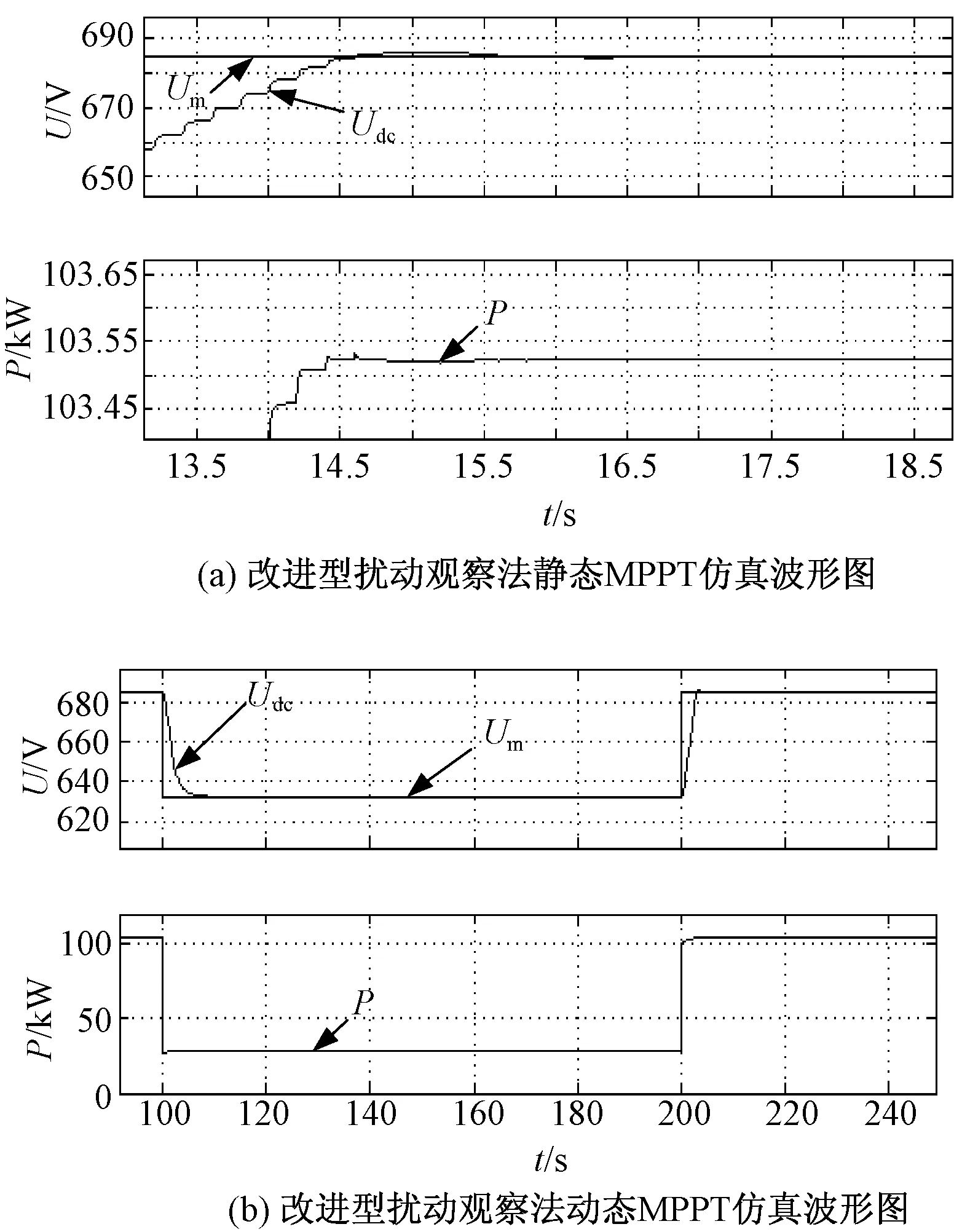
图8 改进型扰动观察法MPPT仿真波形图Fig.8 Simulation waveforms of improved perturbation and observation algorithm

因此，由仿真波形及效率可知，改进型扰动观察法的MPPT效率高，降低了系统能量损失，对提高系统效率具有优势。

4.3 样机实验

样机实验采用100kW光伏并网逆变器，依照CGC/GF 035:2013规定的实验方法，对样机进行了MPPT效率测试。

表1～表4为MPPT效率测试中的部分实验结果。静态效率表中，电压为PV模拟器I-V特性曲线的MPP电压(最低运行电压为500V, 最高运行电压为800V)，功率比值为PV模拟器I-V特性曲线的MPP功率与逆变器的额定DC输入功率比值，加权效率为不同电压下的加权静态MPPT效率，表中结果为不同电压和功率比值条件下的静态MPPT效率。动态效率实验中辐照度区间为300～1000W/m2，测试开始前等待时间为180s, 每组实验循环次数为10。

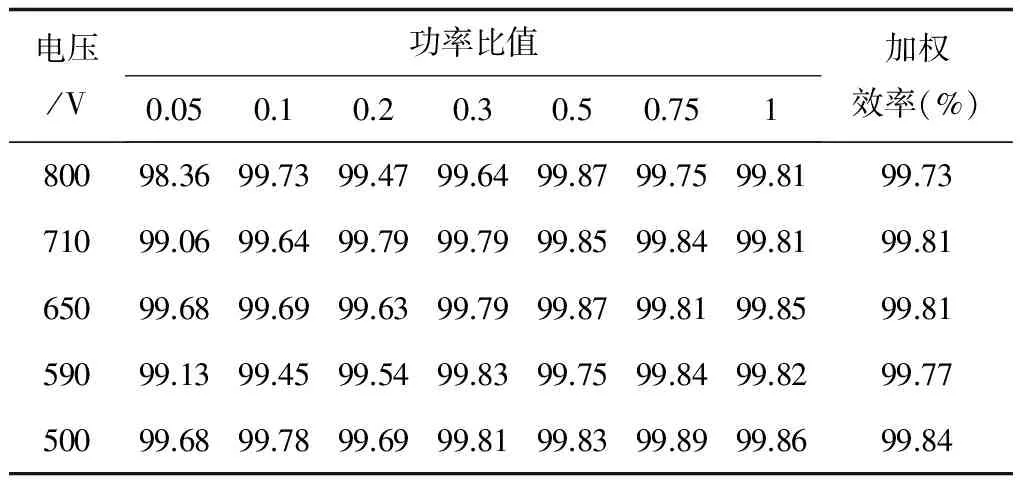
表1 改进型电导增量法静态MPPT效率表

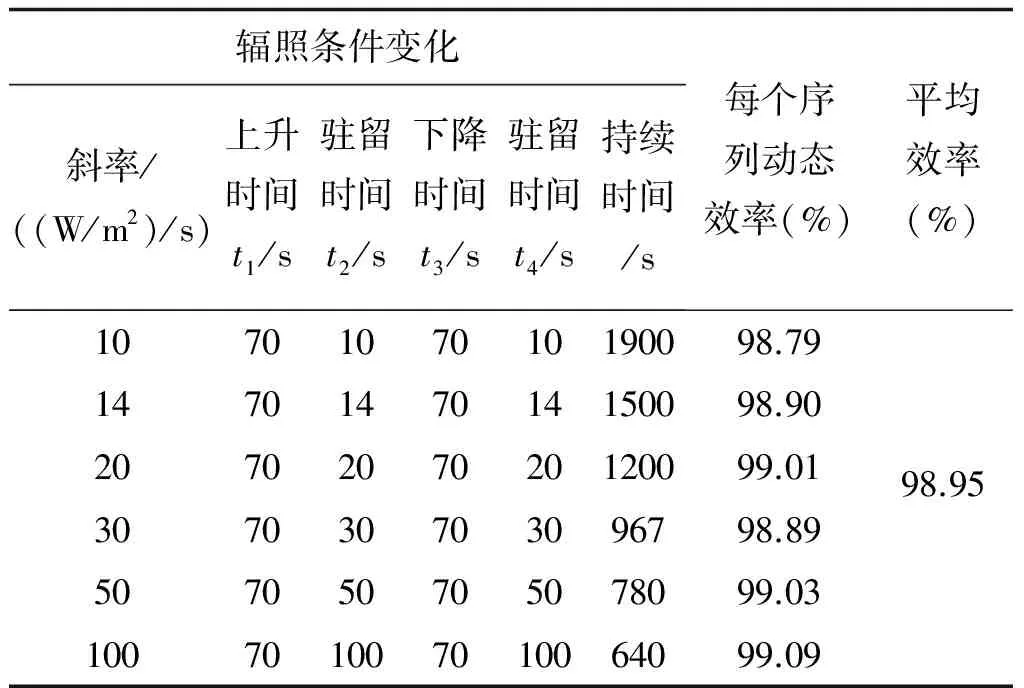
表2 改进型电导增量法动态MPPT效率表

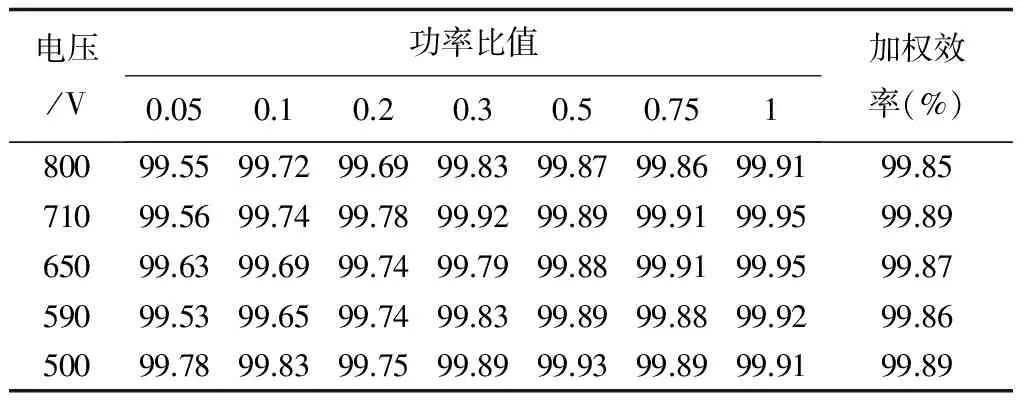
表3 改进型扰动观察法静态MPPT效率表

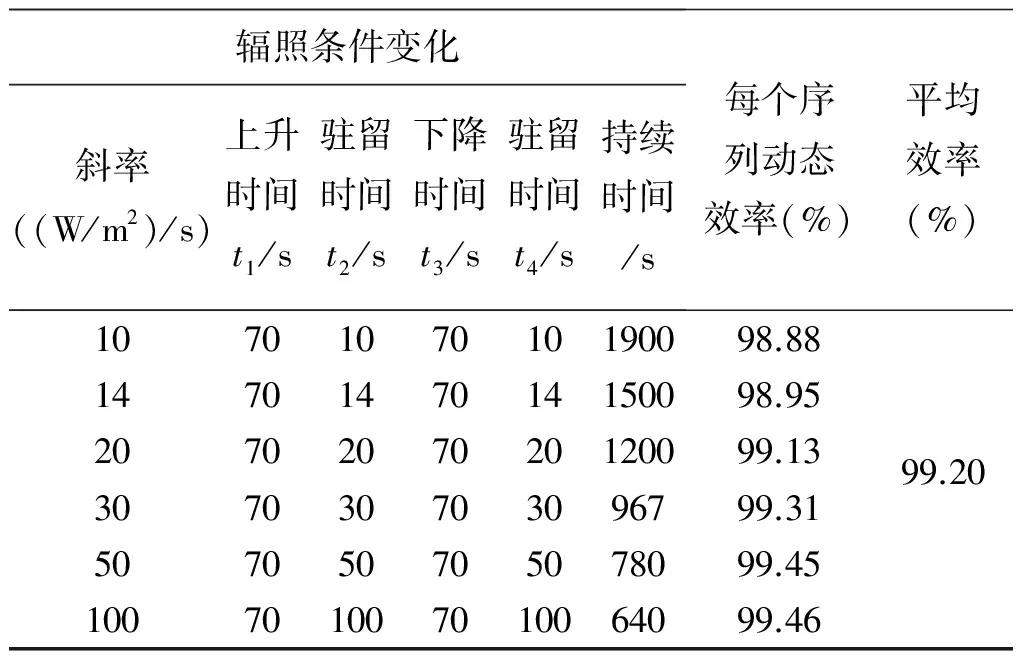
表4 改进型扰动观察法动态MPPT效率表

对比两种方法的静态MPPT效率和动态MPPT效率可以得出，改进型扰动观察法的综合MPPT效率更高。图9为应用改进型扰动观察法对应的100kW逆变器满功率稳态输出电压、电流波形。

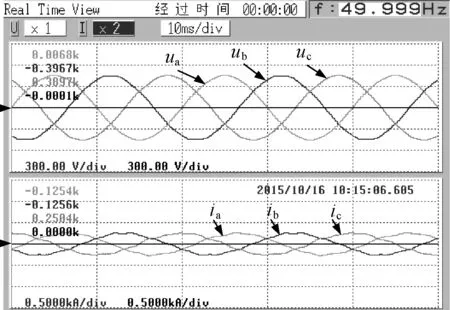
图9 逆变器输出电压、电流实验波形Fig.9 Current and voltage experiment waveforms of inverter output

5 结论

本文针对目前产品中应用最多的电导增量法和扰动观察法两种MPPT方法进行了比较分析，并分别提出能够有效提升动态性能以及静态跟踪精度的改进型算法，仿真结果表明改进型算法均能够得到较好的动静态性能。其中，扰动观察法因算法简单、跟踪效率较高，更适合在实际产品中应用。

[1] 刘邦银，段善旭，刘飞，等(Liu Bangyin,Duan Shanxu,Liu Fei,et al.)．基于改进扰动观察法的光伏阵列最大功率点跟踪(Photovoltaic array maximum power point tracking based on improved perturbation and observation method)[J]．电工技术学报(Transactions of China Electrotechnical Society)，2009，24(6)：91-94．

[2] 李晶，窦伟，徐正国，等(Li Jing,Dou Wei,Xu Zhengguo,et al.).光伏发电系统中最大功率点跟踪算法的研究(Research on MPPT methods of photovoltaic power generation system)[J].太阳能学报(Acta Energiae Solaris Sinica)，2007，28(3)：268-273.

[3] 沈旦立，李振璧，皇淼淼，等(Shen Danli,Li Zhenbi,Huang Miaomiao,et al.).基于改进滞环比较法的光伏阵列MPPT(Photovoltaic array maximum power point tracking based on improved hysteresis comparison method)[J].电力电子技术(Power Electronics)，2012，46(9)：4-6，15.

[4] 杨旭，曾成碧，陈宾(Yang Xu,Zeng Chengbi,Chen Bin).基于广义动态模糊神经网络的光伏电池MPPT控制(MPPT control of photovoltaic cells based on generalized dynamic fuzzy neural network)[J].电力系统保护与控制(Power System Protection and Control)，2010，38(13)：22-25.

[5] Altasa I H, Sharaf A M. A novel maximum power fuzzy logic controller for photovoltaic solar energy systems [J]. Renewable Energy, 2008, 33(3): 388-399.

[6] Platon Baltas. The Arizona University photovoltaic designer program (ASUPVD) [R]. Phoenix：Department of Electrical and Computer Engineering, Arizona State University, 1996.

[7] 周东宝，陈渊睿(Zhou Dongbao,Chen Yuanrui).基于改进型变步长电导增量法的最大功率点跟踪策略(Maximum power point tracking strategy based on modified variable step-size incremental conductance algorithm)[J].电网技术(Power System Technology)，2015，39(6)：1491-1498.

[8] Valentini M, Raducu A, Sera D, et al. PV inverter test setup for European efficiency, static and dynamic MPPT efficiency evaluation [A]. 11th International Conference on Optimization of Electrical and Electronic Equipment [C]. 2008. 433-438.

[9] Haeberlin H, Borgna L, Kaempfer M, et al. Measurement of dynamic MPP-tracking efficiency at grid-connected PV inverters [A]. 21st European Photovoltaic Solar Energy Conference [C]. 2006.

Comparison research of two improved variable step length MPPT algorithm

PAN Yi-kun, DOU Wei

(Beijing Corona Science & Technology Co. Ltd.， Beijing 100083， China)

Photovoltaic array maximum power point tracking technology is one of the key technologies of the application of photovoltaic power generation. In this paper, based on the academic research, the variable step length incremental conductance algorithm and the perturbation and observation algorithm MPPT technologies which are the most practical application algorithm were optimized and the advantages and disadvantages are compared in detail. Comparing the results of simulations and experiments, the improved perturbation and observation algorithm could be more accurately and faster track the maximum power point, and is more suitable for the actual product.

MPPT； photovoltaic grid-connected inverter； incremental conductance algorithm； perturbation and observation algorithm

2015-11-10

国家高技术研究发展计划(863计划)资助项目(2011AA05A303)

潘逸菎 (1987-)， 男， 北京籍， 工程师， 硕士， 研究方向为大功率变流技术； 窦 伟 (1977-)， 男， 河北籍， 高级工程师， 博士， 研究方向为新能源发电技术。

TM72

A

1003-3076(2016)03-0069-07