Excel在不同椭球地理坐标到大地坐标转换中的应用*

杨勇军，侯青青

(江西有色地质勘查二队，江西 赣州　341000)



Excel在不同椭球地理坐标到大地坐标转换中的应用*

杨勇军，侯青青

(江西有色地质勘查二队，江西 赣州341000)

摘要：文章给出了高斯—克吕格投影正算及参数间相互关系转换公式，利用其转换公式，对中国现有3种地理坐标系(1954北京坐标系、1980西安坐标系和2000国家大地坐标系)坐标在Excel单元格中编制相应的语句进行换算，并给出具体的换算公式和与之对应的Excel语句及已编制好的换算表格。实践证明，这种方式表格能实现地理坐标系到大地坐标系坐标的自动转换，大地坐标3°和6°的互换带，使烦琐换算变得程序化、自动化。

关键词：高斯—克吕格投影；大地坐标；地理坐标；坐标转换；换带

0引言

根据国家地理信息测绘局发布的公告，中国从2008年7月1日起启用2000国家大地坐标系，衔接的过渡期为8至10年[1]。随着时间的推移，现过渡期将满，届时中国原有各类测绘成果将面临转换成2000国家大地坐标系工作。中国现常用测绘坐标系有1954年北京坐标系、1980西安坐标系，2000国家大地坐标系3种，先前测绘成果采用1980西安坐标系或1954年北京坐标系，因此，将面临大量测绘成果坐标转换成2000国家大地坐标系过程。本文根据高斯—克吕格投影正算原理，按其公式和各坐标系统椭球参数，编制Excel计算表格，将这3种坐标系地理坐标换算到大地坐标，让烦琐坐标转换计算变得简单，只需在相应单元地址中输入待转换地理坐标、相应坐标系统以及分带号即可完成转换到大地坐标系的任务[1-4]。

1高斯—克吕格投影坐标公式

高斯—克吕格投影的X、Y计算公式如下：

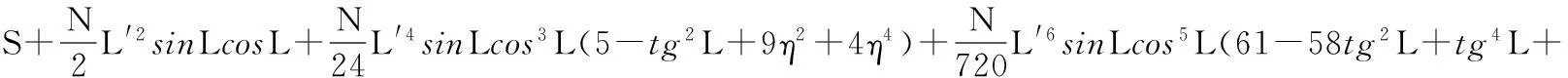
270η4-330η2tg2L)

(1)

(2)

式中：L为地理坐标纬度；L′为该点到其所在投影带中央经线的经差，以弧度计。当L′以“度”为单位时，应变为“弧度”后代入：

L′=(L-L0)π/180

(3)

设某点的地理位置为L(L，B)，其中L为纬度，B为经度，按下式可求投影带号n：

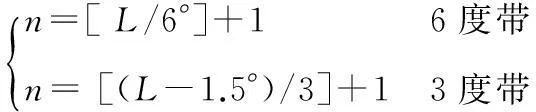
(4)

式中：[]为取整符号。对于东半球来说，投影带的中央经线为：

(5)

N为地球椭球卯酉圈曲率半径，计算公式为：

(6)

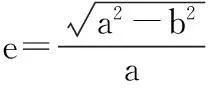
η=e′cosL

(7)

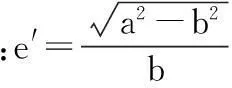
由赤道到纬度L的子午线弧长S的计算公式为：

S=AL-Bsin2L+Csin4L-Dsin6L+Esin8L

(8)

系数A、B、C、D、E为第一偏心率的函数；

(9)

式(9)中A′、B′、C′、D′、E′的计算公式为：

(10)

式中：a为地球椭球长半径，以m为单位；e为第一偏心率[2，3]。

2不同椭球地理坐标到大地坐标在Excel中语句的编制

新建Excel工作簿，设定B2单位格地址是“坐标系统名称”栏，根据待转地理坐标系名称，输入相应的系统名称即可，此表只提供1954、1980、2000三种坐标系的数据转换，其它坐标系会自动默认为1980西安椭球参数。

设定B3单位格是输入“投影带号”栏，此表支持3°带和6°带两种分带模式，其它分带法将会在G5单位格中显示“FALSE”，表其后计算数据不正确，在G5单元格中输入“=IF(BMYM3=3，F5*3，IF(BMYM3=6，(F5*6-3)))”语句实现，其中“MYM”表示单元格绝对地址，只要在单元格行、列前使用该符号，使用“复制”命令时就不会自动增加表格的行、列数。

分别在F3、G3单位格中输入“=IF(BMYM2>1954，IF(BMYM2=2000，6378137，6378140)，6378245)、=IF(BMYM2>1954，IF(BMYM2=2000，6356752.31414，6356755.2882)，6356863.0188)”语句，它将根据B2单元格输入坐标系统返回相应椭球长半轴值，短半轴值。

在F5单元格中输入“=IF(BMYM3=3，INT((D5-1.5)/3)+1，INT((D5)/6)+1)”语句，同理它会根据B3单元格输入“带号”，计算出相应大地坐标带号。

在现实中，“度”通常用六进制“度分秒”表示，而Excel中却是用十进制“度”表示，故将转换成六进制“度分秒”形式，用“=INT(经纬度)+(INT(经纬度*100)-INT(经纬度)*100)/60+(经纬度*10000-INT(经纬度*100)*100)/3600”语句实现。

在M5中录入“=IF(L6<6，L6*PI()/180，"错误")”，语句含义根据输入带号来返回相应的计算值，当带号不等于3或6时，返回值是“错误”字符，表示表格将无法计算；其中“=经纬度*PI()/180” 是度转弧度公式语句，‘PI()’是Excel中的π值，由赤道到纬度L的子午线弧长计算，若按(8)式来编制，在Excel中将很难实现，为了便于在表格中编制，同时满足不同椭球计算，将式(8)转化为：

S=A×L- 1.9958102LsinLcosL- 7.95835102Csin3LcosL-

31.34517297Dsin5LcosL

(11)

式(8)最后一项“Esin8L”，因其计算值总是小于0.000 03 m[3]，故式(11)已将其省略；在N5单元格编制Excel语句“=JMYM3*E5-1.9958102*KMYM3*SIN(L5)*COS(L5)-7.95835102*LMYM3*SIN(L5)^3*COS(L5)-31.34517297*MMYM3*SIN(L5)^5*COS(L5)”计算弧长值。

其它单元格语句都是严格按照高斯投影正算公式编制，见表1。

按照表1，在Excel对应单元格编制语句，编制好的计算表格见表2，表格第5行是已编制好语句并可以自动计算单元格，使用复制命令，填充到其它空白行，表格会自动按编制好公式进行填充语句进行转换计算，从而实现批量计算。

为便于美观，只需将成果计算单元格显示，其余辅助计算单元格隐藏。最终展现结果，见表3。

表1在Excel中不同椭球地理坐标到投影坐标语句的编制表

Tab.1The establishment of transformation statements from different ellipsoidal geographic coordinates to projection coordinates in Excel

表2　在Excel中不同椭球地理坐标到投影坐标计算表

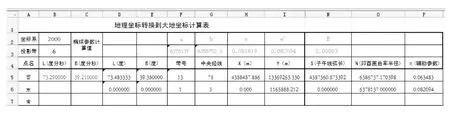
表3　在Excel中不同椭球地理坐标到投影坐标计算表Tab.3　The calculation results of transformation from different ellipsoidal geographic coordinates to projection coordinates in Excel

3实例验算

本文坐标验算选用4个点，采用2000国家大地坐标系，6度分带法，选取中国某区域东、南、西、北4点。选用坐标换带计算软件(V5.0版)和本文编制的Excel表格分别换算，验证结果见表4。

4结论

在不同的坐标系中采用不同的椭球参数和椭球定位，由于任何坐标系中的椭球，其地理坐标的定义是一致的，即某点的经度从零子午线起算，纬度则从赤道起算。所以，不同的椭球，必然存在地理坐标相同的同名点[2]。这样，本文在Excel单元格中编制坐标换算公式，及参数间相互关系公式，通过编制语句让表格自动换算坐标，只要在B2单元格中输入不同坐标系名称，B3单元格确定待算点分带法，就能将国内现在常用的3种地理坐标转变为大地坐标；同时，巧妙利用分带号，就能实现3°换6°、6°换3°的大地坐标互换计算。本文给出了具体换算公式和已编制好的Excel计算表格及与之对应Excel语句，并结合实例，通过和专用换算软件相比，X最大差值-0.85 mm，Y最大差

表4　软件与编制Excel表格换算坐标数据对比表

值+0.96 mm。从验证结果可见，利用本文编制的表格进行坐标转换完全能满足精度，且在Excel环境下编制地理坐标转换到大地坐标计算表，具有以下特点：

1)编制方便，易于掌握。

2)透明度高。Excel的运算过程高度透明可见，其中大量采用了引用数据，给计算带来了方便，通过语句复制实现批量转换，减少工作量的同时能进行交互式的人机对话，查错在前台。

3)实用性强。计算表格编制好后，只需将其它待算点输入到相应的单元格中，修改目标坐标系名称及投影带号，就能自动计算出相应的大地坐标，无须重复编制，且可使用复制命令批量转换，这将对此类工作带来诸多便利，同时也提高了工作效率，减少了劳动强度[4]。

[参考文献]

[1]立实.2000国家大地坐标系7月1日启用 [N].中国测绘，2008-06-27.

[2]孔祥元，郭际明.控制测量学：下册[M].武汉：武汉大学出版社，2006：1-20.

[3]钟业勋，童新华，王龙波.从1980西安坐标系到2000国家大地坐标系的坐标变换[J].海洋测绘，2010，30(1)：1-3.

[4]杨勇军，黄奎树，欧阳云.利用Excel表格进行导线的近似平差计算[J].科技与生活，2012，9(9)：221-223.

Application of Excel in Transformation Between Different Ellipsoidal Geographic Coordinates and Geodetic Coordinates

YANG Yong-jun，HOU Qing-qing

(No.2TeamofJiangxiNonferrousMetalsGeologicalExplorationBureau，GanzhouJiangxi341000，China)

Abstract：The formulas of Gauss-Kruger projection directly-calculation and the transformation relationships of all the parameters are presented in this paper. The transformation formulas are used to convert the coordinates between three kinds of geographic coordinates in China (1954 Beijing coordinate system, 1980 Xi’an coordinate system and 2000 national geodetic coordinate system) through the preparation of the corresponding statement in Excel cell address. The specific transformation formulas and corresponding Excel statements, and transformation table are given. All the facts proves that the method can achieve the automatic transformation of coordinates from the geographic coordinates system to the geodetic coordinates system, and realize the exchange between 3° belt and 6° belt, and making the cumbersome transformation process become automatic.

Key words：Gauss-Krueger projection; geodetic coordinates; geographic coordinates; transformation of coordinates; exchange belt

作者简介：杨勇军(1982～)，男，江西吉水人，学士，工程师，现主要从事工程测量与项目管理方面的工作。

中图分类号：P 226+.3

文献标识码：B

文章编号：1007-9394(2016)01-0046-04

收稿日期：2015-06-02

地矿测绘2016，32(1)：46～49

CN 53-1124/TDISSN 1007-9394

Surveying and Mapping of Geology and Mineral Resources