减载控制灵敏度及其在广域低频保护中的应用
2016-05-24杨德友蔡国伟
杨德友,蔡国伟
(东北电力大学 电气工程学院,吉林 吉林 132012)
0 引言
频率是电力系统运行的重要技术指标之一[1],与系统有功发电-有功负荷平衡状态密切相关,频率稳定的本质是有功平衡问题[2]。随着世界范围内能源战略的实施,大规模能源基地、大容量输电通道逐步投入运行,系统由于故障引起的大规模功率缺额的概率也逐渐增大,电网频率稳定问题日益突出[3]。
低频减载作为第3道防线,是保证大规模功率脱落后电力系统安全稳定运行的重要控制手段[4-6]。传统低频减载方案多采用离线设计、在线应用的模式加以实现[7],通常存在过切负荷和频率悬停等问题,已很难满足动态频率具有明显“时空分布”特征的大规模电力系统安全稳定控制的需求[8]。基于广域信息的广域保护(国外称为特殊保护系统)与控制WAPC(Wide Area Protection and Control)理论和方法随着广域测量系统技术的应用得到了快速的发展[9-10]。作为广域保护与控制理论的重要组成部分,基于广域信息的自适应低频减载也受到了国内外专家学者的广泛关注。文献[11]以惯性中心坐标下系统等效转子运动方程为基础,提出了基于广域信息的功率缺额估计模型,并根据缺额估计值设计了减载方案。文献[12-13]提出了计及负荷电压特性的自适应低频减载策略,旨在提高功率缺额的估计精度。
现有文献中广域自适应低频减载的研究中多关注系统受扰后功率缺额估计模型的研究,而对于减载地点选取和减载量分配的研究鲜有涉及。因此,本文通过对多机系统有功扰动后动态频率响应特征的分析,构建了负荷节点减载控制灵敏度,并以减载控制灵敏度为基础实现了减载地点选取和减载量分配的实时决策。IEEE 10机39节点系统仿真结果表明,本文设计的减载控制方案及提出的减载控制灵敏度具有优良的控制性能,相比于传统控制方案和措施,在相同的控制代价下,能够获得更加快速的频率恢复速度和更接近系统额定运行频率的稳态值。
1 减载控制灵敏度模型
早期电网覆盖区域较小,系统联系紧密,可忽略机组之间的相互影响,多采用单机模型对动态频率特性进行分析。但随着电力系统的发展,覆盖区域更加广阔的大型互联电网逐渐形成,系统的动态频率特性已转为由系统中分布在不同位置的发电机和负荷共同作用决定,具有明显的“时空分布”特征。
1.1 有功扰动分配特征
假设在如图1所示的网络中,负荷节点k处发生扰动PΔ,将整个网络收缩为发电机内电势节点和负荷扰动节点k。由于功率扰动的发生,导致发电机组的有功出力与负荷的平衡关系被打破,不平衡功率在机组间重新进行分配,系统随即进入暂态过程。
在节点k施加扰动后,直接结果就是节点k的电压相角发生改变,由 δk0变为 δk0+δkΔ,而由于机组惯量的作用,机组节点内角度不能发生突变。在仅考虑线路电抗的前提下,对节点有功功率表达式进行线性化处理,可得发电机和扰动负荷节点的有功变化分别为[14]:
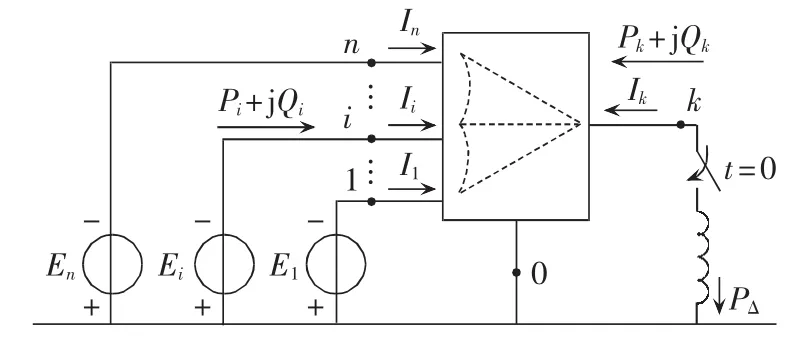
图1 节点k发生扰动时的简化网络Fig.1 Simplified network when disturbance occurs at node k
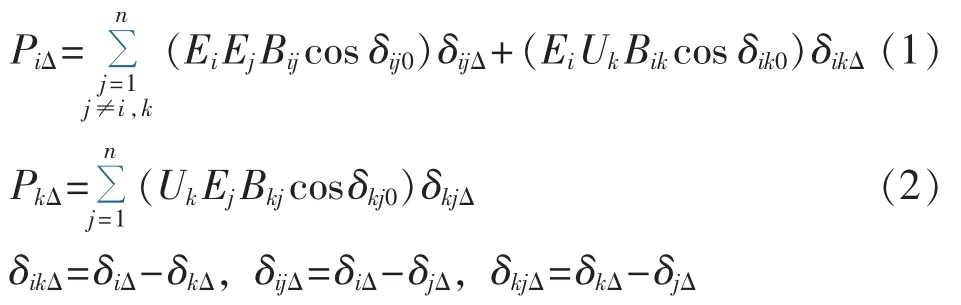
其中,Ei为机组i的内电势;Bij为节点i与节点j间的电纳;Uk为节点k的电压。
定义同步功率系数 PSij=EiEjBijcosδij0、PSik=EiUk×Bikcos δik0和 PSkj=UkEjBkjcosδkj0,代入式(1)、(2)中有:

当t=0+时,由于发电机组的惯性作用,相角δi不能突变,则 δiΔ=0,δijΔ=0,δikΔ=-δkΔ(0+),δkjΔ=δkΔ(0+)。
则式(3)和式(4)可以表示为:

由式(5)可以看出,发电机机组i分担的不平衡量功率 PiΔ(0+)由同步功率系数 PSik和 δkΔ(0+)决定,而系统中的所有机组 δkΔ(0+)是相同的,因此,机组所分担的扰动功率实际取决于同步功率系数PSik。
考虑节点k受扰后,系统有功不平衡功率由各机组分担,显然下式成立:
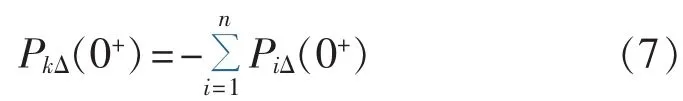
将式(5)、式(6)两端交叉相乘可得:

由式(8)可以得出扰动初始时刻第i台机组所承担扰动量为:
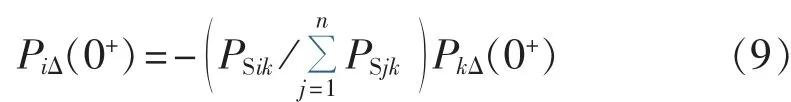
式(9)表明有功扰动故障瞬间各发电机组分担的扰动功率根据同步功率系数进行分配。通过分析同步功率系数表达式PSik=EiUkBikcos δik0可以看出,电纳Bik越大,初始角度δik0越小,机组分担的扰动功率也越大,亦即距离扰动点越近,机组承担的有功缺额份额越大。
1.2 基于扰动分配特征的减载控制灵敏度
根据1.1节多机电力系统动态频率响应特征分析可知,当电网某处发生有功扰动时,各发电机拾取的有功扰动量主要由发电机与扰动节点间的同步功率系数决定,即假设当负荷节点i处切除大小为ΔPLi的负荷时,发电机j拾取的扰动量为:
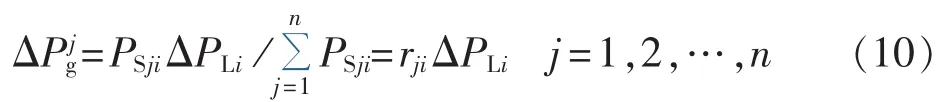
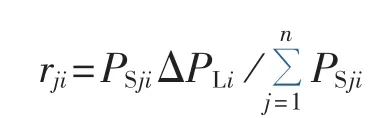
当发电机j的有功负荷因节点i处负荷切除而发生变化时,发电机j的频率偏差可由其拾取的有功扰动量和发电机的调差系数共同决定,其表达式为:
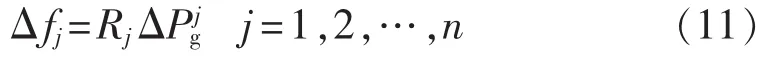
其中,Rj为发电机j的调差系数。
系统平均频率偏差可以利用系统内各发电机组频率偏差和等值转动惯量计算获得[11]:
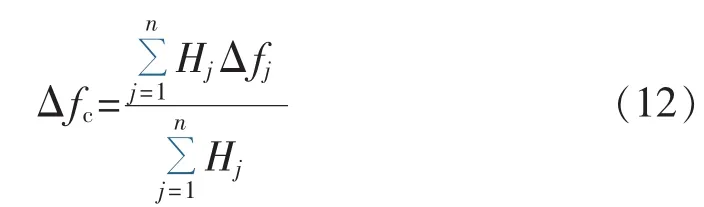
其中,Hj为发电机j的等值转动惯量。
系统平均频率偏差对负荷节点i有功变化的灵敏度Si可以表示为系统平均频率偏差与负荷节点i处负荷切除量的比值,即:

将式(10)和式(12)代入式(13)可得:

式(14)为本文提出的基于频率响应特征的减载灵敏度,可以看出,减载灵敏度以多机电力系统频率响应过程中有功扰动分配特征为基础,并计及了发电机组及调速器的动态特性,能够准确反映不同负荷节点在切除等量负荷时对系统频率动态过程的影响程度。
由式(14)可以看出,本文提出的负荷节点减载控制灵敏度大小主要由系统内运行发电机转动惯量Hi、发电机调差系数Ri及负荷节点与扰动节点间的同步功率系数 PSji(因为)共同决定。但Hi和Ri为发电机固有特征参数,与负荷节点无关,因此,各负荷节点减载控制灵敏度主要由负荷节点与扰动节点间的同步功率系数决定,即与负荷节点与扰动节点间的电气距离直接相关。
2 基于减载控制灵敏度的广域低频保护
2.1 有功缺额估计模型
为实现系统遭受有功扰动后紧急状态下的频率控制,很多文献提出了基于扰动瞬间频率变化率的有功功率缺额估计模型,该估计模型通常以等值单机系统为基础,利用惯性中心模型对全系统功率缺额进行估计[11]:

其中,He为系统等值转动惯量;dfcoi(0+)/dt为系统惯性中心下的瞬时频率变化率。
式(15)所示的有功缺额估计模型主要利用发电机组频率动态信息,但频率(变化)是功率(差额)的积分,受发电机调节和负荷响应等共同影响。由于在有功缺额的同时往往伴随有无功缺额,功率扰动后负荷侧电压将有所降低,这就使得式(15)的估计结果通常要小于实际缺额量。目前,在广域自适应低频减载中,比较广泛采用的处理方式是对利用式(15)计算得到的功率缺额量进行修正,以获取功率缺额估计的准确值,即[15]:

本文将利用式(15)和式(16)估计功率缺额。
式(15)和式(16)所示的功率缺额估计方法是建立在系统全部发电机均安装有同步相量测量单元(PMU)基础上的,这就使得全部发电机信息可实时获取,当某台发电机退出运行后,可以根据量测信息实时计算系统损失的惯性时间常数,进而利用式(15)和式(16)准确估算功率缺额。该方法是目前广域低频减载方案中常用的功率缺额估算方法,详见文献[11-12]和[15]。
2.2 减载地点选取及减载量分配方案
通过减载灵敏度的推导和分析可知,在不同负荷节点切除等量负荷时,系统频率动态特性也不尽相同,减载灵敏度越大表明该负荷节点在减载控制过程中对系统频率动态特性影响越大;在减载灵敏度较大的负荷节点处切除负荷量越大,越有利于系统频率的快速恢复,因此,本文以减载灵敏度为基础,设计实现了2种减载地点选取和减载量分配方案,具体描述如下。
方案A:在不同负荷节点切除等量负荷时,系统频率动态特性也不尽相同,减载灵敏度越大表明该负荷节点在减载控制过程中对系统频率动态特性影响越大;在减载灵敏度较大的负荷节点处切除负荷量越大,越有利于系统频率的快速恢复。方案A的流程具体如图2所示。

图2 方案A减载地点选取流程Fig.2 Flowchart of load shedding location selection by scheme A
对可切负荷节点,按照灵敏度从大到小进行排序,进而按照如图2所示的流程选择灵敏度之和超过全部可切节点减载灵敏度之和30%的前m个节点作为减载地点。对减载量ΔPLS在所选取的m个节点间进行分配,各负荷节点减载量为:
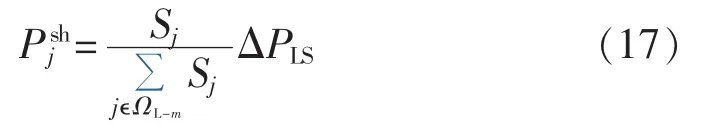
其中,ΩL-m为所选取的m个负荷节点集合。
需要说明的是,方案A中的30%为人为设定值,可以根据系统实际情况和电网规模,并结合调度运行人员经验提前设定。
方案B:首先对可切负荷节点按灵敏度从大到小进行排序,切除灵敏度较大负荷节点的全部负荷,直至所切负荷大于等于减载量ΔPLS,具体流程见图3。

图3 方案B减载地点选取流程Fig.3 Flowchart of load shedding location selection by scheme B
上述即为本文设计的2种基于减载控制灵敏度的广域低频保护与控制方案,本文将在第3节对2种方案进行计算、对比和分析。
本文提出的基于减载控制灵敏度的广域低频保护策略依赖于广域相量测量系统实时获取扰动瞬间发电机频率信息估计功率缺额,同时将减载方案和减载指令通过广域相量测量系统下发至相关配置有低频减载装置的变电站。
3 仿真与分析
本文以如图4所示的IEEE 10机39节点系统作为仿真系统对减载控制灵敏度的有效性进行分析[16]。该系统有19个负荷节点,其中节点39为等值系统,其所带负荷亦为等值负荷,不在本区的可控范围内,假设为不可切负荷,节点31为发电机节点,其所带负荷为厂用负荷,假设为不可切负荷,则系统可切负荷节点集为{3,4,7,8,12,15,16,18,20,21,23,24,25,26,27,28,29}。
本文将对如下2种功率扰动进行计算和分析。
算例1:母线38处的发电机G9因故障切除,系统损失功率830 MW。

图4 IEEE 10机39节点系统结构图Fig.4 Structure of IEEE 10-generator 39-bus system
算例2:母线32处的发电机G3因故障切除,系统损失功率830 MW。
2种故障方式下各可切负荷节点的减载控制灵敏度见图5,节点按灵敏度由大到小的排序见表1。
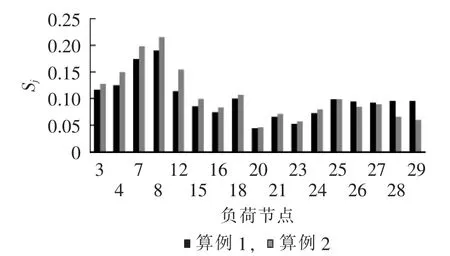
图5 负荷节点减载控制灵敏度Fig.5 Load shedding control sensitivities of load nodes
分别采用减载方案A和方案B对算例1和算例2扰动后系统进行控制,同时对减载量平均分配方案的控制效果进行计算和分析。
各低频减载装置动作频率为49.5 Hz,时间延时为0.2 s,其中,0.2 s的延时主要用于防止实际应用为中通信及算法处理延时而引起的低频减载装置误动。
算例1:故障后根据扰动瞬间量测信息,利用式(15)和式(16)估计功率缺额,结果为802.3 MW。方案A选取负荷节点8、7、4、3作为减载地点,各节点减载比例分别为48.15%、98.08%、33.27%和48.21%;方案B减载节点为8、7、4,各节点减载比例分别为100%、100%和9.12%。各方案减载控制后系统频率动态过程如图6所示,控制性能统计结果如表2所示。
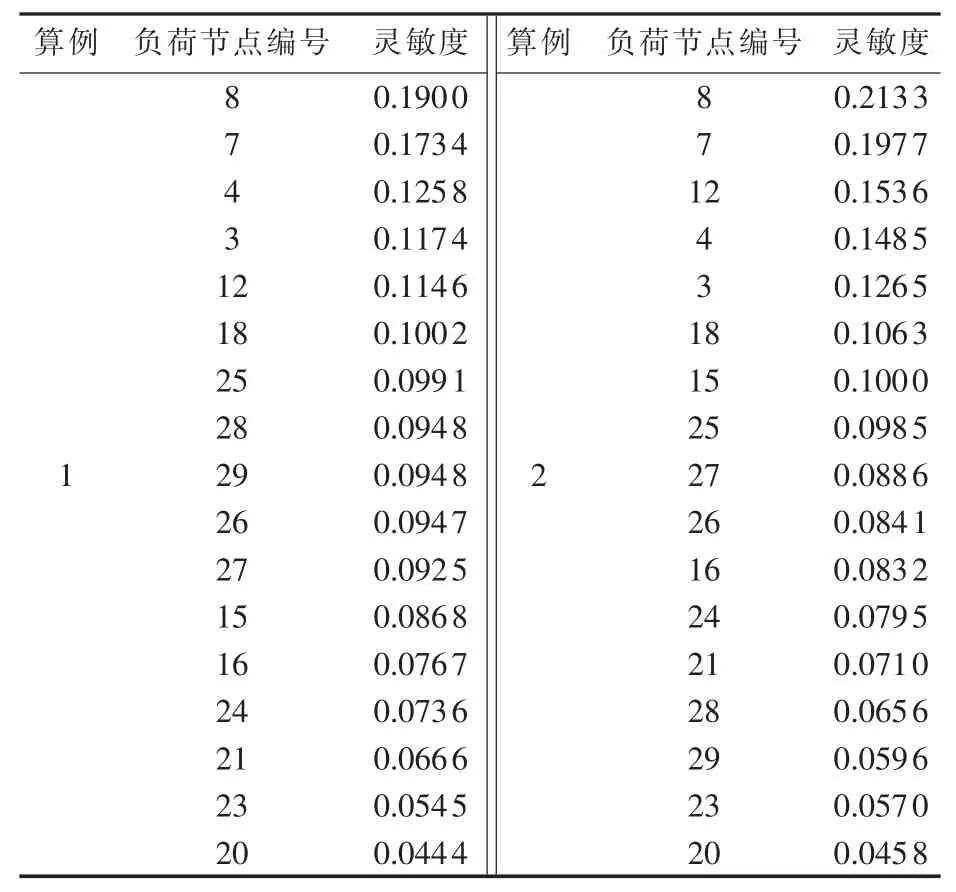
表1 灵敏度排序结果Table1 Ranking of load shedding control sensitivity
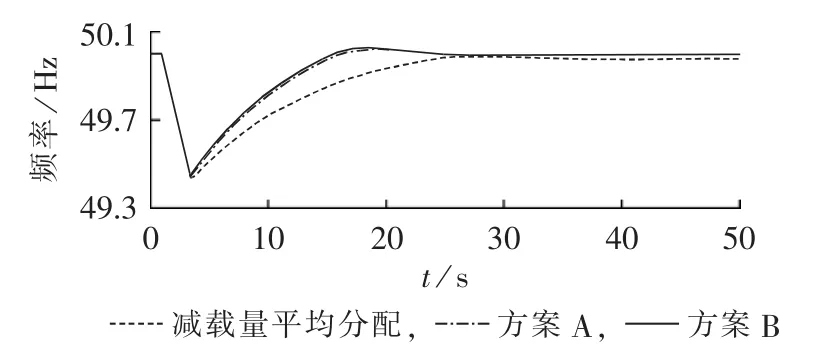
图6 算例1的频率动态响应曲线Fig.6 Dynamic frequency response curves of case 1
算例2:相同故障后根据扰动瞬间量测信息,并利用式(15)和式(16)估计功率缺额,结果为824.6 MW。方案A中选取的减载负荷节点为节点8、7、12,各节点的减载比例分别为73.43%、100%和100%,其中节点7和节点12负荷全部切除的主要原因是其负荷值小于按式(17)计算得到的应分担切负荷量,需将剩余减载量分配至节点8;方案B中的减载节点为节点8、7,各节点减载比例分别为100%和43.88%。各方案减载控制后系统频率动态过程如图7所示,控制性能统计结果亦参见表2。
从上述2种扰动方式的计算结果不难看出,本文提出的以多机电力系统频率响应特征为基础的减载灵敏度能够定量反映在切除等量负荷时,各负荷节点对系统频率动态响应的影响程度,由计算结果可以看出不同扰动方式下,各负荷节点的减载灵敏度也不同。进而根据基于减载灵敏度的减载地点选取和减载量分配原则对各扰动方式中估计所得的有功缺额量在利用不同方案所选取的负荷节点间进行分配,计算结果表明,在切除等量负荷的前提下,相对减载量平均分配方案,本文提出的减载地点选取和减载量分配原则在低频持续时间和稳态频率2个控制性能指标上具有一定的优势,尤其对于功率缺额量较大的算例1,本文方案控制效果的优势更加明显。

表2 控制性能对比结果Table 2 Comparison of control performance

图7 算例2的频率动态响应曲线Fig.7 Dynamic frequency response curves of case 2
4 结论
基于有功扰动后多机电力系统功率分配特征和频率响应特性,推导出了负荷节点减载控制灵敏度,并以减载控制灵敏度为基础实现了减载量分配的实时决策。仿真实验结果表明,本文设计的减载控制方案及提出的减载控制灵敏度具有优良的控制性能,在相同的控制代价的前提下,能够获得更加快速的频率恢复速度和更接近系统额定运行频率的稳态值。对于指导智能电网环境下大规模电网低频减载地点选取和减载量分配具有重要的意义。
必须指出,本文的研究工作还有待深入探索,如考虑如何在减载过程中考虑电压变化的影响是今后需要进一步研究的课题。
[1]中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会.电力系统频率偏差:GB/T15945—2008[S].北京:中国电力出版社,2008.
[2]KUNDUR P.Power system stability and control[M].New York,USA:McGraw-Hill Professional,1994.
[3]宋兆欧,刘俊勇,刘友波,等.计及动态修正的自适应广域低频减载[J]. 电力自动化设备,2014,34(4):95-100,119.SONG Zhaoou,LIU Junyong,LIU Youbo,etal.WAMS-based adaptive UFLS considering dynamic correction[J].Electric Power Automation Equipment,2014,34(4):95-100,119.
[4]AHSAN M Q,CHOWDHURY A H,AHMED S S,et al.Technique to develop auto load shedding and islanding scheme to prevent power system blackout[J].IEEE Transactions on Power Systems,2012,27(1):198-205.
[5]高翔,高伏英,杨增辉.华东电网因直流故障的频率事故分析[J].电力系统自动化,2006,30(12):102-107.GAO Xiang,GAO Fuying,YANG Zenghui.Frequency accident analysis in East China Grid due to DC line fault[J].Automation of Electric Power Systems,2006,30(12):102-107.
[6]袁季修.防止电力系统频率崩溃的紧急控制[J].电力自动化设备,2002,22(4):1-4.YUAN Jixiu.Emergency control for preventing frequency collapse of power system[J].Electric Power Automation Equipment,2002,22(4):1-4.
[7]国家能源局.电力系统自动低频减负荷技术规定:DL/T428—2010[S]. 北京:中国电力出版社,2011.
[8]YANG Deyou,CAI Guowei.Spatial characterization of the dynamic response[J].International Journal of Emerging Electric Power Systems,2013,14(2):139-148.
[9]de la REE J,CENTENO V,THORP J S,et al.Synchronized phasor measurement applications in power systems[J].IEEE Trans on Smart Grid,2010,1(1):20-27.
[10]VALVERDE G,CAI Deyu,REGULSKI P,et al.Wide-area monitoring,protection,and control of future electric power networks[J].Proceedings of the IEEE,2011,99(1):80-92.
[11]TERZIJA V V.Adaptive load shedding based on the magnitude of the disturbance estimation[J].IEEE Transactions on Power Systems,2006,21(3):1260-1266.
[12]时伯年.考虑联络线约束的跨区电网低频减载系统的研究[D].北京:清华大学,2007.SHI Bonian.Under frequency load shedding scheme for interconnected power grid with consideration of the tie line constraint[D].Beijing:Tsinghua University,2007.
[13]熊小伏,李东晋.基于在线负荷检测的变电站低频减载方案[J].电力自动化设备,2011,31(9):32-35.XIONG Xiaofu,LI Dongjin.Under-frequency load shedding based on online load detection for electric substations[J].Electric Power Automation Equipment,2011,31(9):32-35.
[14]ANDERSON P M,FOUAD A A.Power system control and stability[M].2nd ed. [S.l.]:Wiley-IEEE Press,2003.
[15]SEYEDIH,SANAYE-PASAND M.New centralizedadaptive load-shedding algorithms to mitigate power system blackouts[J].IET Gener Transm Distr,2009,3(1):99-114.
[16]蔡国伟.电力系统暂态稳定性的支路暂态势能分析方法[D].哈尔滨:哈尔滨工业大学,1999.CAI Guowei.Branch transient potential energy analysis method for power system transient stability[D].Harbin:Harbin Institute of Technology,1999.
