新型同塔双回高压直流输电线路分布参数测量方法及工程应用
2016-05-24郝艳捧
邓 军 ,肖 遥 ,郝艳捧
(1.华南理工大学 电力学院,广东 广州 510640;2.中国南方电网 超高压输电公司检修试验中心,广东 广州 510663)
0 引言
同塔双回高压直流输电线路已应用于我国“溪洛渡”西电东送工程,该工程具有输电走廊占地面积少、建设速度快、输送能力强、节省投资等优势。国内相关机构研究了同塔双回直流线路的极性布置、空间离子电流密度、控制保护策略、感应电压及电流等技术[1-3]。线路参数的理论计算方法主要采用经典的CARSON公式,因沿线大地电阻率的不断变化,采用该方法计算长距离同塔双回线路参数时理论计算值与实际值具有较大的误差[4]。为此,同塔双回高压直流输电线路系统仿真、继电保护整定、线路故障测距等所需线路参数以实际测量值为准[5-10]。
对于交流同塔双回线路,国内已采用基于全球定位系统(GPS)的带电测量方法进行了互感线路参数的测试,该方法测量线路参数时存在并行线路两端测量装置安装困难和相量测量单元(PMU)采样精度低的问题[11-13]。传统单端法采用双曲函数泰勒级数展开式的前几项近似逼近中等长度线路,能够有效地提高线路参数的测量精度,但对于长距离高压输电线路有限项泰勒级数的截断误差随线路增长而增大[14-16]。文献[17-18]提出了一种基于区内发生缺相运行状态测量计算交流线路正、负、零序参数的方法,在电力系统安全稳定运行的前提下该方法要求运行单位将线路处于非全相运行状态进行线路参数测量的现实操作性极小。针对目前国内外未见同塔双回直流线路参数测试方法的现状,结合上述传统交流线路参数测量方法存在的不足,提出同塔双回高压直流输电线路分布参数测试方法。
本文建立同塔双回高压直流输电线路分布参数的物理模型,结合同塔双回直流线路末端对地开路、短路接地的边界条件,推导同塔双回线路不同组合方式下线路分布参数的数学方程组,给出同塔双回高压直流输电线路单位长度电阻、自电感、自电容、耦合电容及耦合电感测量计算的解析公式,搭建长线路直流线路等值实验模型,验证高压直流输电线路分布参数测量方法测量精度的可靠性,并开展牛寨至广东±500kV同塔双回直流线路及接地极线路参数的测试与分析。
1 同塔双回高压直流输电线路分布参数计算模型
同塔双回高压直流输电线路分布参数计算模型如图1所示。假设同塔双回高压直流输电线路为均匀的平行传输线,在线上任一点x处取线元dx,因线元dx远小于波长,可采用集中参数电路进行线元dx的计算。假设导线A1、A2、B1、B2的自感 LA1D、LA2D、LB1D、LB2D相等;各导线的对地电容 CA1D、CA2D、CB1D、CB2D相等;各导线的电阻值和对地电导均分别为R和G;导线A1和A2的互感MA1A2等于导线B1和B2的互感MB1B2;导线A1和B1的互感MA1B1等于导线A2和B2的互感MA2B2;导线A1和B2的互感MA1B2等于导线A2和B1的互感MA2B1;导线A1和A2的耦合电容CA1A2等于导线B1和B2的耦合电容CB1B2;导线A1和B1的耦合电容CA1B1等于导线A2和B2的耦合电容CA2B2;导线A1和B2的耦合电容CA1B2等于导线A2和B1的耦合电容CA2B1。
当同塔双回高压直流输电线路导线A1、A2、A3和A4首端短路,施加频率为ω的单相电源时,根据基尔霍夫定律建立电路方程,采用常微分方程进行求解,得到:
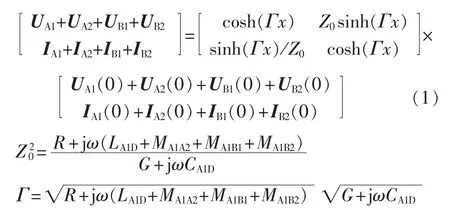
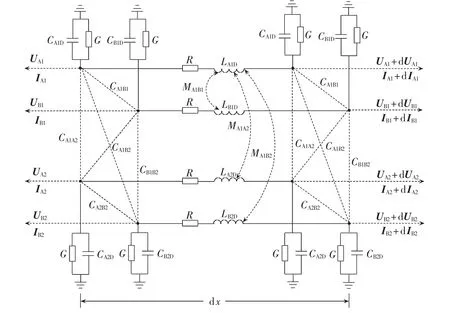
图1 同塔双回高压直流输电线路分布参数模型Fig.1 Distributed parameter model of dual-loop HVDC transmission lines on same tower
其中,UA1(0)、UA2(0)、UB1(0)、UB2(0)和 IA1(0)、IA2(0)、IB1(0)、IB2(0) 分别为导线 A1、A2、B1、B2首端 x=0 处的电压和电流。
当高压直流输电线路末端x=l处开路时,各导线末端电流 IA1(l)、IA2(l)、IB1(l)、IB2(l)都为 0,测量各导线首端 x=0 处的电压 U1A1(0)、U1A2(0)、U1B1(0)、U1B2(0),以及各导线首端电流 I1A1(0)、I1A2(0)、I1B1(0)、I1B2(0)。当高压直流输电线路末端x=l处短路接地时,各导线末端电压 UA1(l)、UA2(l)、UB1(l)、UB2(l)等于 0,测量各导线首端 x=0 处的电压 U2A1(0)、U2A2(0)、U2B1(0)、U2B2(0),以及各导线首端电流 I2A1(0)、I2A2(0)、I2B1(0)、I2B2(0)。将上述测量量代入式(1)整合后得到式(2)。
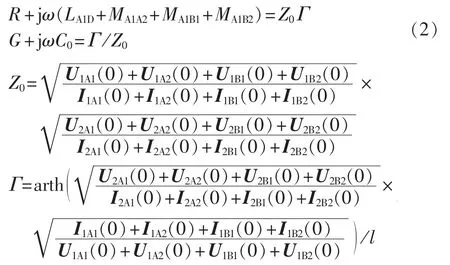
当同塔双回高压直流输电线路导线A1和A2首端短路,导线B1和B2首端短路,施加频率为ω、相位相差180°的两相对称电源时,根据基尔霍夫定律建立电路方程,采用常微分方程进行求解,得到式(3)。

其中,U3A1(0)、U3A2(0)、U3B1(0)、U3B2(0)和 I3A1(0)、I3A2(0)、I3B1(0)、I3B2(0)分别为高压直流输电线路末端 x=l处于开路时各导线首端的电压和电流;U4A1(0)、U4A2(0)、U4B1(0)、U4B2(0)和 I4A1(0)、I4A2(0)、I4B1(0)、I4B2(0)分别为高压直流输电线路末端x=l处短路接地时各导线首端的电压和电流。
当同塔双回高压直流输电线路导线A1和B1首端短路,导线A2和B2首端短路,施加频率为ω、相位相差180°的两相对称电源时,根据基尔霍夫定律建立电路方程,采用常微分方程进行求解,得到式(4)。
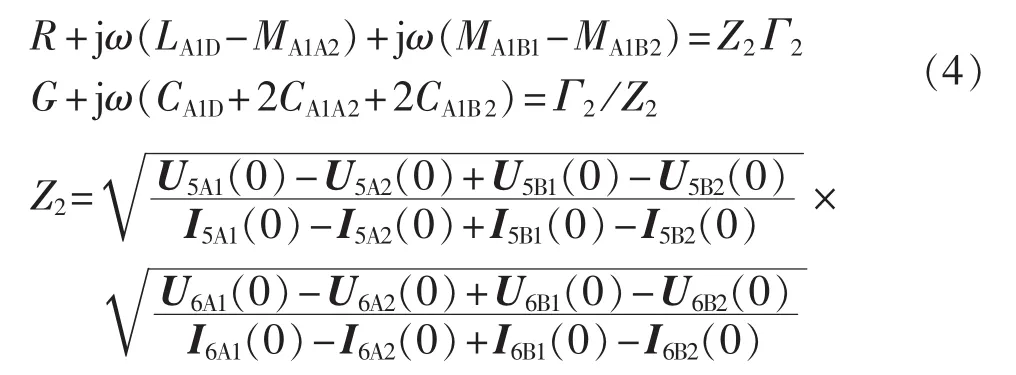
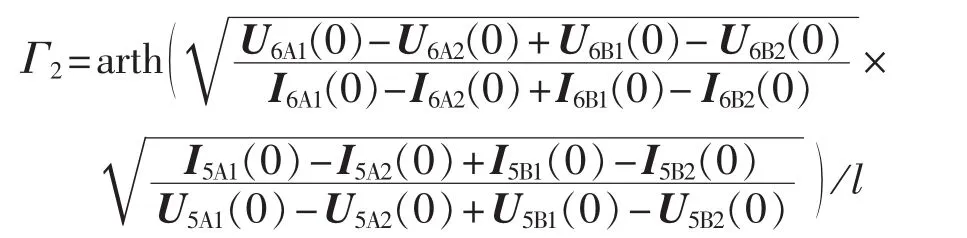
其中,U5A1(0)、U5A2(0)、U5B1(0)、U5B2(0)和 I5A1(0)、I5A2(0)、I5B1(0)、U5B2(0)分别为高压直流输电线路末端 x=l处开路时各导线首端的电压和电流;U6A1(0)、U6A2(0)、U6B1(0)、U6B2(0)和 I6A1(0)、I6A2(0)、I6B1(0)、I6B2(0)分别为高压直流输电线路末端x=l处短路接地时各导线首端的电压和电流。
当同塔双回高压直流输电线路导线A1和B2首段短路,导线A2和B1首端短路,施加频率为ω、相位相差180°的两相对称电源时,根据基尔霍夫定律建立电路方程,采用常微分方程进行求解,得到式(5)。
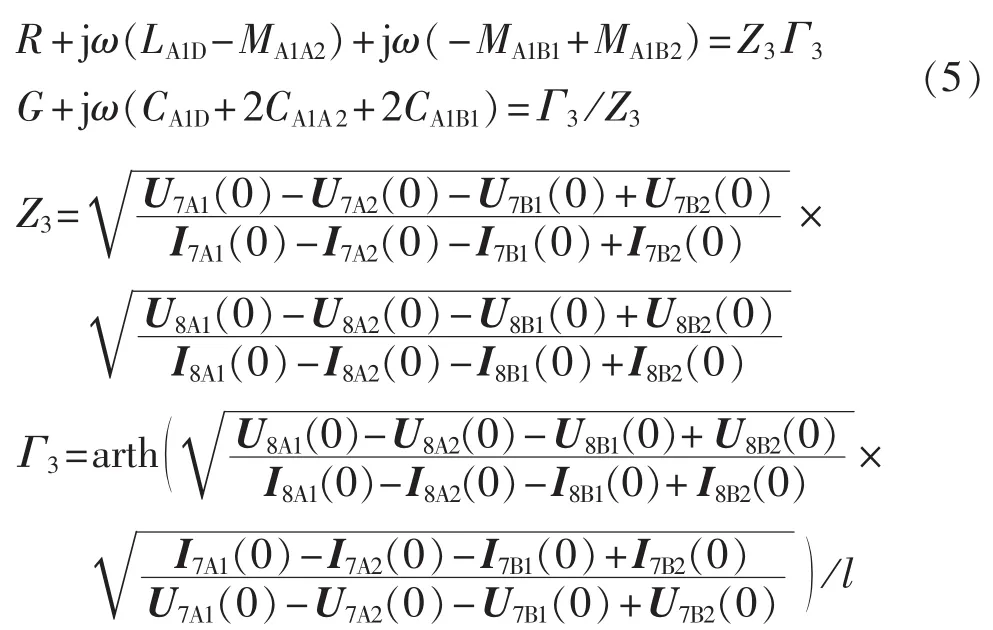
其中,U7A1(0)、U7B1(0)、U7A2(0)、U7B2(0)和 I7A1(0)、I7A2(0)、I7B1(0)、I7B2(0)分别为高压直流输电线路末端 x=l处开路时各导线首端的电压和电流;U8A1(0)、U8A2(0)、U8B1(0)、U8B2(0)和 I8A1(0)、I8A2(0)、I8B1(0)、I8B2(0)分别为高压直流输电线路末端x=l处短路接地时各导线首端的电压和电流。
联立式(2)—(5),得到高压直流同塔双回输电线路单位长度的电阻、自电感、自电容、耦合电容、耦合电感如式(6)所示。
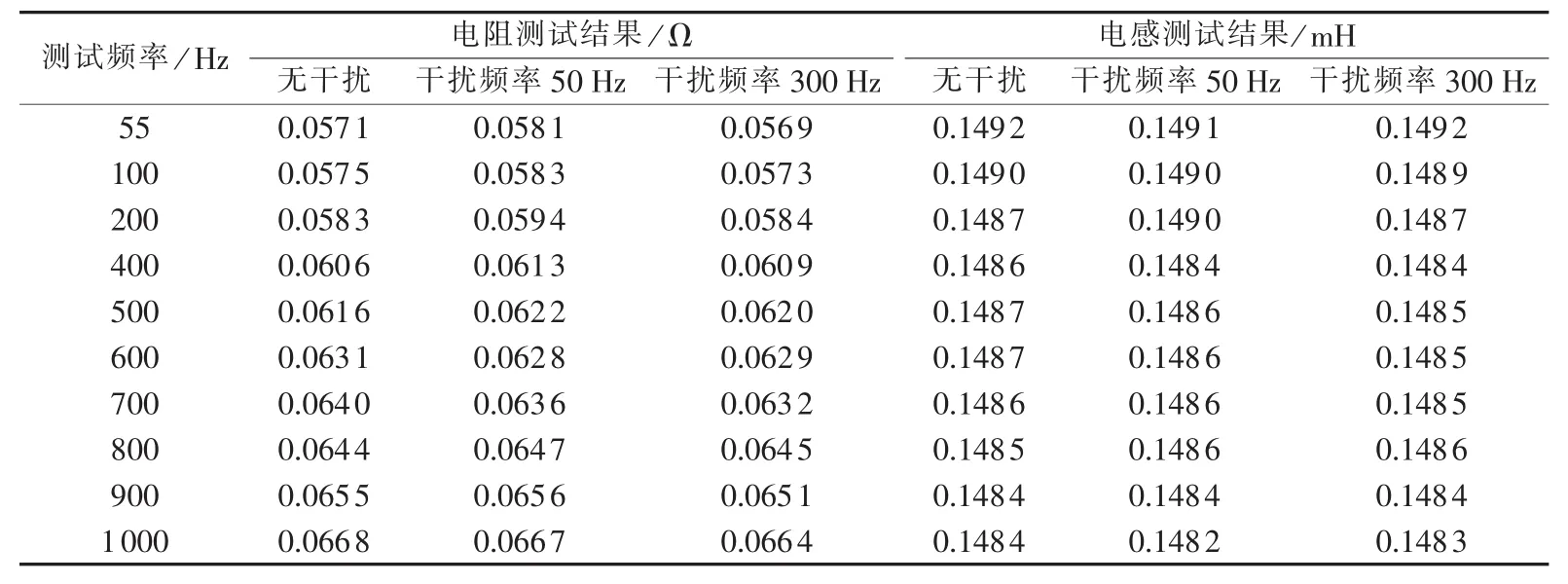
表1 不同干扰信号下实验模型的分布参数测量结果Table 1 Distributed parameter measurements of experimental model for different interference signals
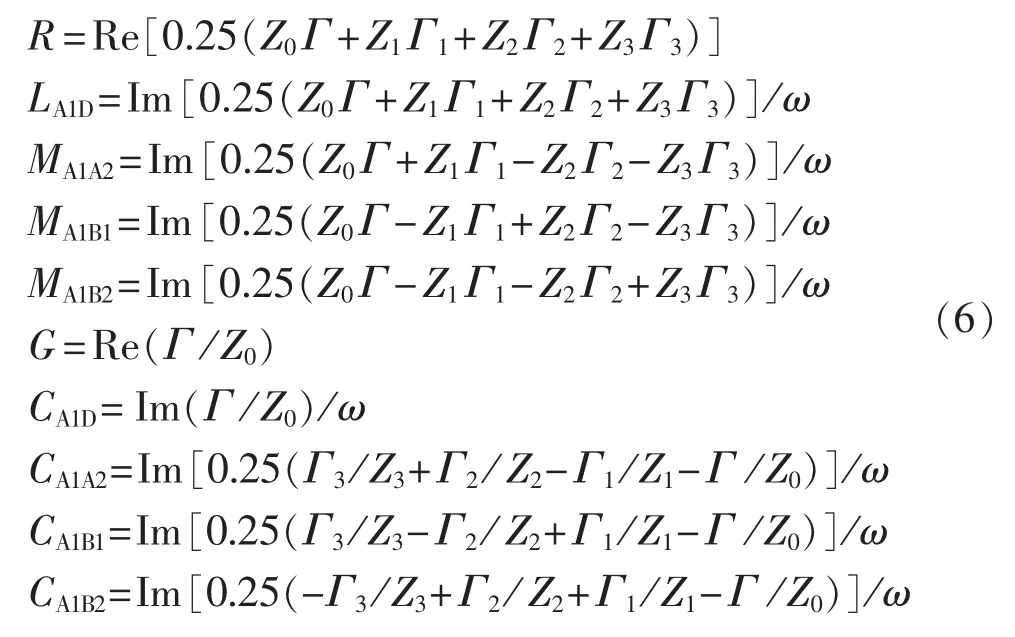
2 同塔双回高压直流输电线路分布参数测量方法的验证与应用分析
2.1 测试方法实验模型的验证与分析
为验证上述同塔双回高压直流输电线路分布参数测试方法的有效性,搭建了等效直流输电线路1000 km的实验模型,分别在实验模型中对无干扰信号、50 Hz干扰信号、300 Hz干扰信号3种工况下的分布参数进行测量,测量信号的频率分别为55 Hz、100 Hz、200 Hz、300 Hz等 10 个频率段,测量结果如表1所示。不同测试频率下,50 Hz干扰信号时的电阻值与无干扰信号的测量结果最大误差为7.3%,最小误差为1.3%;不同测试频率下,300 Hz干扰信号时的电阻值与无干扰信号的测量结果最大误差为5.3%,最小误差为3.4%。不同测试频率下,50 Hz干扰信号时的电感值与无干扰信号的测量结果最大误差为1.3%,最小误差为0.3%;不同测试频率下,300Hz干扰信号时的电感值与无干扰信号时的测量结果最大误差为1.6%,最小误差为0.6%。因此,基于等效直流输电线路1000 km实验模型分布参数测量结果表明该测量方法具有可靠的精度,满足工程误差要求。
2.2 牛寨至广东同塔双回高压直流线路参数测试与分析
结合牛寨至广东同塔双回高压直流工程,该线路全长 1225 km,导线类型 JL /G1A-900 /75,分裂数为4。采用异频法(40~60 Hz),分别将逆变站的双极四导线处于对地开路、短路接地的方式,在整流站对正序组合(组合1为甲1和甲2短接且乙1和乙2短接;组合2为甲1和乙2短接且乙1和甲2短接;组合3为甲1和乙1短接且甲2和乙2短接)施加幅值相等、相位互差180°的电源,记录各种方式下的导线首端的电压、电流相量;将逆变站的双极四导线分别处于对地开路、短路接地的状态,在整流站短接甲1、甲2、乙1和乙2,施加幅值相等、相位相等的电源,记录导线首端的电压、电流相量。牛寨至广东同塔双回高压直流线路分布参数测量值如下。
a.自参数测量值:电阻为0.0096 Ω /km,自电感为 2.0686 mH /km,自电容为 0.0028 μF /km。
b.耦合电感测量值:甲1对甲2为2.3981mH/km;甲1对乙1为2.2689 mH/km;甲1对乙2为2.2818 mH /km。
c.耦合电容测量值:甲1对甲2为0.0063μF/km;甲1对乙1为0.0063 μF/km;甲 1对乙 2为 0.0064 μF/km。
所得结果表明:单位长度导线电阻值为0.0096 Ω/km;单根导线的自感小于线路间互感,其最大差值为0.3295 mH/km;单根导线的自电容小于各回导线间的耦合电容,其最大差值为0.0036 nF/km,线间耦合电容基本相等。
2.3 牛寨换流站同塔双回直流接地极线路参数测试与分析
牛寨换流站同塔双回接地极线路全长123km,导线类型NRLH60GJ-300/40,分裂数为2。采用异频法(40~60 Hz),分别将接地极本体处的2组导线处于对地开路、短路接地(将接地点引至接地极本体,禁止将接地点直接接在终端塔的接地网)的方式,在牛寨换流站进行不同组合方式下的开路阻抗和短路阻抗测量,通过计算得到牛寨换流站高压直流接地极线路参数测量值如下。
a.自参数测量值:电阻为0.053 Ω/km,自电感为 2.8362 mH /km,自电容为 0.0025 μF /km。
b.耦合电感测量值:甲1对甲2为1.6400mH/km;甲1对乙1为1.6684 mH/km;甲1对乙2为1.6723 mH /km。
c.耦合电容测量值:甲1对甲2为0.0083μF/km;甲1对乙1为 0.0041 μF/km;甲1对乙 2为 0.0049 μF /km。
结果表明:单位长度导线电阻值为0.053 Ω/km;单根导线的自感大于线路间互感,其最大差值为1.1962 mH/km;单根导线的自电容小于各回导线间的耦合电容,其最大差值为0.0058 nF/km,线间耦合电容最大差值为0.0042 nF/km。
2.4 从西换流站同塔双回直流接地极线路参数测试与分析
从西换流站高压直流工程接地极线路全长144 km,导线类型 NRLH60GJ-300/40,分裂数为 2。采用异频法(40~60 Hz),分别将接地极本体处的2组导线处于对地开路、短路接地(处理方式同牛寨站接地极)、在从西换流站测量不同组合方式下的开路阻抗和短路阻抗值,通过计算得到从西换流站高压直流接地极线路参数测量值如下。
a.自参数测量值:电阻为0.053 Ω/km,自电感为3.1318 mH /km,自电容为 0.0025 μF /km。
b.耦合电感测量值:甲1对甲2为2.73mH/km;甲1对乙1为2.66 mH/km;甲1对乙2为2.65mH/km。
c.耦合电容测量值:甲1对甲2为0.0086μF/km;甲1对乙1为0.0044 μF/km;甲1对乙2为0.0054 μF /km。
结果表明:单位长度导线电阻值为0.053 Ω/km;单根导线的自感大于线路间互感,其最大差值为0.4818 mH/km;单根导线的自电容小于各回导线间的耦合电容,其最大差值为0.0061 nF/km,线间耦合电容最大差值为0.0042 nF/km。
3 结论
a.建立了同塔双回高压直流输电线路分布参数的物理模型,提出了在线路首段分别施加幅值相等、相位互差180°的正序电源测量正序组合(组合1为甲1和甲2短接且乙1和乙2短接;组合2为甲1和乙2短接且乙1和甲2短接;组合3为甲1和乙1短接且甲2和乙2短接)的开路阻抗和短路阻抗;并在线路首段分别施加幅值、相位都相等的零序电源测量零序组合(甲1、甲2、乙1、乙2短接)的开路阻抗和短路阻抗,代入方程组计算同塔双回高压直流输电线路单位长度电阻、自电感、自电容、线间耦合电容、线间耦合电感。
b.搭建了等效直流输电线路1000 km的实验模型,开展了在无干扰、50 Hz干扰及300 Hz干扰下10个不同测试频率的线路参数测量,电阻和电感测量结果的最大误差分别为7.3%和1.6%,验证了本文提出的同塔双回高压直流线路参数测试方法的有效性。
c.将高压直流线路参数测试方法应用于牛寨至广东高压直流同塔双回输电线路、牛寨换流站接地极同塔双回线路、从西换流站接地极同塔双回线路参数测量。结果表明:牛寨至广东高压直流同塔双回输电线路单根导线的自感、自电容都分别小于线路间互感和互容,线间耦合电容基本相等;牛寨及从西换流站接地极同塔双回线路单根导线的自感大于线路间互感,单根导线的自电容小于各回导线间的耦合电容。
[1]马文超,吴新桥,廖民传.±500 kV同塔双回直流线路的极性布置[J]. 南方电网技术,2010,4(6):58-60.MA Wenchao,WU Xinqiao,LIAO Minchuan.The polarity arrangement of±500 kV DC lines with double circuits on the same tower[J].Southern Power System Technology,2010,4(6):58-60.
[2]李永明,柴贤东,张淮清,等.±800 kV同塔双回输电线路离子流场的计算[J]. 电力自动化设备,2013,33(6):134-138.LI Yongming,CHAI Xiandong,ZHANG Huaiqing,et al.Calculation of ion flow field for±800 kV transmission line of double circuit on same tower[J].Electric Power Automation Equipment,2013,33(6):134-138.
[3]张烁,李永丽,李博通.高压直流输电系统开路电压的研究[J].电力自动化设备,2015,35(11):95-102.ZHANG Shuo,LI Yongli,LI Botong.Open line voltage of HVDC transmission system[J].Electric Power Automation Equipment,2015,35(11):95-102.
[4]龚有军,林婉欣.超、特高压输电线路高频参数计算方法[J].南方电网技术,2009,3(1):12-16.GONG Youjun,LIN Wanxin.The calculation method for highfrequency parameters of EHV /UHV transmission lines[J].Southern Power System Technology,2009,3(1):12-16.
[5]高淑萍,索南加乐,宋国兵,等.基于分布参数模型的直流输电线路故障测距方法[J]. 中国电机工程学报,2010,30(13):75-80.GAO Shuping,SUONAN Jiale,SONG Guobing,et al.Fault location method for HVDC transmission lines on the basis of the distributed parameter model[J].Proceedings of the CSEE,2010,30(13):75-80.
[6]夏经德,张向聪,黄新波,等.基于纵向阻抗的双端量故障测距新算法[J]. 电力自动化设备,2015,35(10):133-138.XIA Jingde,ZHANG Xiangcong,HUANG Xinbo,et al.Fault locating based on longitudinal impedance according to dual-terminal variables[J].Electric Power Automation Equipment,2015,35(10):133-138.
[7]高厚磊,陈学伟,刘洪正,等.基于改进参数检测法的双端非同步数据故障测距算法[J]. 电力自动化设备,2014,34(9):27-32.GAO Houlei,CHEN Xuewei,LIU Hongzheng,et al.Two-terminal asynchronous data fault location algorithm based on improved parameter detection method[J].Electric Power Automation Equipment,2014,34(9):27-32.
[8]刘永浩,蔡泽祥,徐敏,等.基于波速优化与模量传输时间差的直流线路单端行波测距新算法[J].电力自动化设备,2012,32(10):72-76.LIU Yonghao,CAI Zexiang,XU Min,et al.Single-end fault location algorithm based on traveling wave speed optimization and modal propagation time difference for DC transmission line [J].Electric Power Automation Equipment,2012,32(10):72-76.
[9]徐敏,蔡泽祥,刘永浩,等.基于宽频信息的高压直流输电线路行波故障测距方法[J]. 电工技术学报,2013,28(1):259-265.XU Min,CAI Zexiang,LIU Yonghao,et al.A novel fault location method for HVDC transmission line based on the broadband travelling wave information[J].Transactions of China Electrotechnical Society,2013,28(1):259-265.
[10]束洪春,司大军,葛耀中,等.T型输电线路电弧故障测距时域方法研究[J]. 电工技术学报,2002,17(4):99-103.SHU Hongchun,SI Dajun,GE Yaozhong,et al.A new time domain method for locating faults on T connecion to three terminal transmission lines[J].Transactions of China Electrotechnical Society,2002,17(4):99-103.
[11]薛志英,梁志瑞.互感线路零序参数在线测量中的参数估计[J].高电压技术,2009,35(4):954-958.XUE Zhiying,LIANG Zhirui.Parameters estimation for zerosequence parameter online measurement of transmission lines with mutual inductance[J].High Voltage Engineering,2009,35(4):954-958.
[12]李澍森,陈晓燕,戚革庆.同塔四回输电线路参数带电测量[J].高电压技术,2006,32(7):17-20.LI Shusen,CHEN Xiaoyan,QI Geqing.Discussion on live line measurement of the parameters of the transmission lines with four-circuit on a tower[J].High Voltage Engineering,2006,32(7):17-20.
[13]孙柯,岳志刚,刘苍松.高压输电线路工频参数的移频测量方法[J]. 高电压技术,2007,33(9):203-205.SUN Ke,YUE Zhigang,LIU Cangsong.The shift frequency measurement method of HVDC transmission lines parameters [J].High Voltage Engineering,2007,33(9):203-205.
[14]HOFMANN L.Series expansions for line series impedances considering different specific resistances,magnetic permeabilities,and dielectric permittivities of conductors,air,and ground [J].IEEE Trans on Power Delivery,2003,18(2):564-570.
[15]AKKE M,BIRO T.Measurements of the frequency-dependent impedance of a thin wire with ground return[J].IEEE Trans on Power Delivery,2005,20(2):1748-1752.
[16]肖遥,李澍森,马骞,等.输电线路分布参数测量方法的改进[J].南方电网技术,2012,6(3):22-27.XIAO Yao,LI Shushen,MA Qian,et al.The improvement of distribution parameters measurement of transmission lines [J].Southern Power System Technology,2012,6(3):22-27.
[17]胡志坚,陈允平,徐玮,等.基于微分方程的互感线路参数带电测量研究与实现[J]. 中国电机工程学报,2005,25(2):28-33.HU Zhijian,CHEN Yunping,XU Wei,et al.Principles and realization of live line measurement of parameters of transmission lines with mutual inductance based on differential equations[J].Proceedings of the CSEE,2005,25(2):28-33.
[18]牛胜锁,梁志瑞,张建华,等.基于多时段同步测量信息的T接线路参数在线测量[J]. 电工技术学报,2012,27(5):238-243.NIU Shengsuo,LIANG Zhirui,ZHANG Jianhua,et al.Online measurement of T-connection transmission line parameters based on multi-interval synchronized measurement information[J].Transactions of China Electrotechnical Society,2012,27(5):238-243.
