考量能量裕度及权重因子的电力系统节点综合脆弱性分析

张 程 ，于永军 ，李华强 ，徐 行

（1.四川大学 电气信息学院，四川 成都 610065；2.国网新疆电力公司电力科学研究院，新疆 乌鲁木齐 830000）

0 引言

电力系统在遭受外部扰动时，母线电压会呈现下降趋势，并逐步趋于崩溃点［1-2］。为防止系统出现大面积电压崩溃，需要构建脆弱性评估指标对当前安全水平以及变化趋势进行预测。脆弱性分析旨在快速准确定位系统中的脆弱环节，提前预防控制，防患于未然。可见，电力系统脆弱性理论研究意义深远。

传统的脆弱性定义为：在扰动或者故障影响下电网的节点电压水平或支路传输能力不断弱化的特性［3-4］。

随着区域电网之间的联系越发紧密，电网的安全与稳定问题显得日益突出，基于安全性及稳定性分析发展而来的脆弱性研究理论在近几年得到飞速发展。国内外脆弱性问题的研究方法主要分为2类［5-6］：基于运行状态的能量函数法及风险概率评估方法等；基于拓扑结构的复杂网络理论及人工智能法等。文献［7］提出了基于无尺度图模型的脆弱性评估方法，将系统所有状态变量处理为有向图中的节点，应用于复杂大网络脆弱性的分析。文献［8］提出基于局部参数法的连续潮流计算，通过对输电线路的过负荷分析和级联故障的发生概率来进行电力系统的脆弱性综合评估。文献［9］在电气介数的基础上提出了电流介数指标，结合最大传输能力分析得出了新的脆弱性评估方法。文献［10］通过构造电网元件模型，将电网母线等效为复杂网络节点，将电网转变为一等效权重图，选取大电网中的薄弱环节。文献［11］从暂态失稳的方面，考虑了天气条件与负荷水平等不确定因素对电网脆弱性的影响，建立故障的概率模型，突出了事故脆弱性和系统脆弱性指标；文献［12］从支路势能角度出发，构建电网支路势能函数模型，以不同支路最大势能作为依据，来评估当前状态与稳定边界状态距离。

然而电力系统元件的脆弱性不仅仅与系统的实时运行参数、网络约束条件等密切相关，而且与元件自身的固有脆弱性紧密联系［13-15］。同时状态脆弱性的分析中应兼顾元件运行水平与临界状态的距离及其脆弱趋势的变化快慢。并且，依据节点的不同电压水平，将状态与结构两方面对综合脆弱性的影响偏重进一步量化。

故本文定义元件综合脆弱性如下：兼具扰动对节点电压水平及支路传输能力的影响和节点/支路退出运行对网络拓扑结构完整性及正常运行状态影响的双重特性。可见，本文对应的状态脆弱指标不仅考虑传统指标中的脆弱趋势变化快慢，而且有效结合了脆弱裕度对元件状态的影响。同时，状态与结构两方面对综合脆弱性的影响不再是简单的线性相乘处理，而是基于节点电压水平，采用权重因子统筹兼顾。

本文基于元件与系统相互影响作用的客观事实，运用启发式能量函数及节点功率平衡等式建立改进后的静态能量函数模型。将节点能量相对电压幅值的变化率与能量裕度相结合，提出更贴近实际工程应用的节点状态因子指标；基于电力系统小世界特性识别方法，依据“发电-负荷”节点对间功率对线路占用比重，综合不同节点发电容量和负荷水平影响，应用电气介数进行结构脆弱性的分析。根据状态和结构两者脆弱性分析方法在不同节点电压水平下对节点综合脆弱性的影响差异，提出相应的权重因子进行更有效的脆弱模型构建，根据所提综合脆弱评估指标辨识系统的薄弱环节，进而有针对性地补偿改进。通过IEEE 30节点系统仿真分析验证所提指标的实用性与可行性。

1 脆弱性模型构建

1.1 节点能量函数模型修正

传统的电力系统能量函数综合考虑与有功功率平衡有关的电压相角及与无功功率有关的电压幅值，建立静态能量函数模型［16］。

节点能量函数的基本公式为：

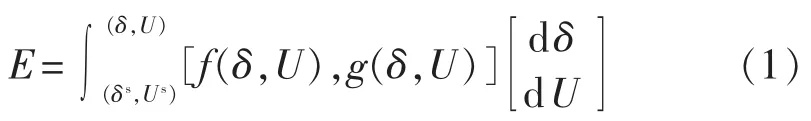
其中，δ、U 和 δs、Us分别为系统的初始状态和当前运行状态的值。

分别将有功功率部分对电压相角积分，无功功率部分对电压幅值积分，可得到在当前状态下的静态能量函数：

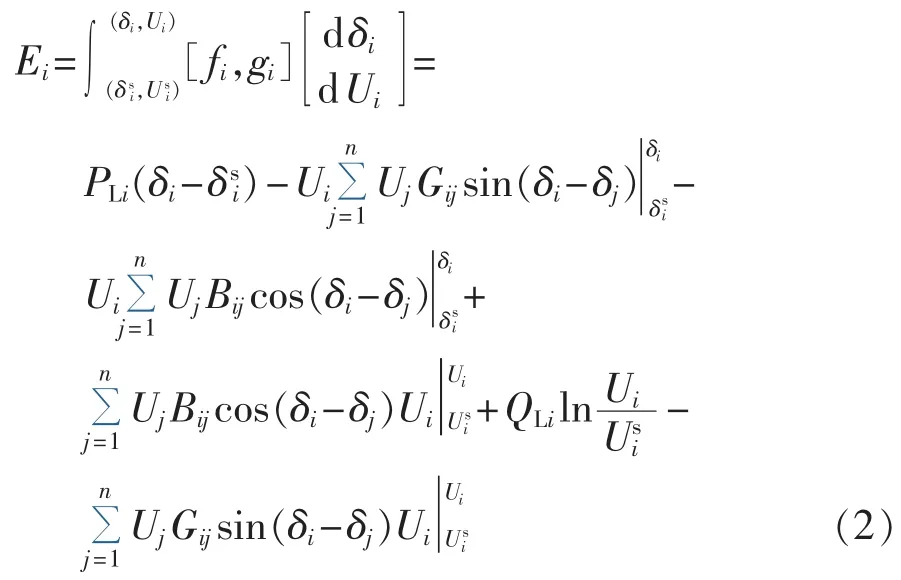
其中，Gij、Bij分别为节点 i、j之间的电导和电纳；Ui、Uj分别为节点 i、j的电压幅值；δi、δj分别为节点 i、j的相角；PLi、QLi分别为节点i的有功、无功负荷；n为系统节点数。

事实上，特别在节点状态脆弱性评估中，无功水平即电压水平对节点运行状态起着决定性作用。然而，式（1）中节点能量同时受到无功水平及有功出力波动的双重影响，故易造成能量增幅较大的节点受到有功出力的误导。实际系统中，致使自身电压水平较高的节点（特别是发电机节点）也被误判为较脆弱的节点，会导致该指标的误分类，与客观运行状况不符。基于此，在能量函数式（1）中剥离有功及相角的影响可以使结果更贴近实际，避免出现误分类。由此将式（1）改进如下：

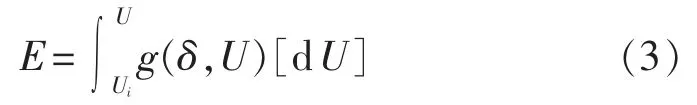
得到更适用于状态脆弱性指标评估的节点静态能量函数：

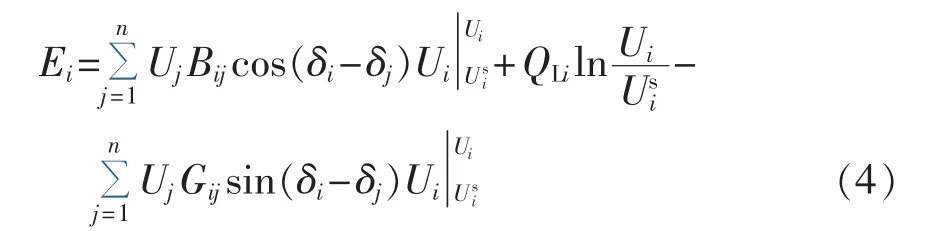
1.2 电气介数模型

本文采用的电气介数指标通过求解电路方程来计算各“发电-负荷”节点对间电流元对各节点的占用情况，量化了各节点在全网潮流传输中的贡献值大小，更符合电力系统的实际物理意义［17］。

根据节点电气介数原理，节点电气介数定义如下：

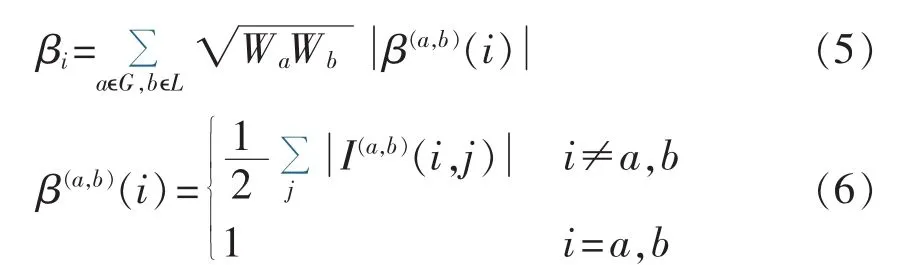
其中，Wa为发电机节点a的权重，取发电机额定容量或实际出力；Wb为负荷节点b的权重，取实际或峰值负荷；G 和 L 分别为发电机节点、负荷节点集合；I（a，b）（i，j）为节点a、b之间注入单位电流源后在支路i-j上产生的电流。

2 脆弱性指标构建

2.1 状态脆弱性指标

根据本文脆弱性指标的新定义，节点的状态脆弱性不仅考虑能量相对于电压幅值的变化趋势，也应将其与节点状态的水平即裕度指标相结合。将当前运行状态下的节点静态能量E0与电压稳定临界点（PV曲线中的鞍结分岔点定义为电压稳定临界点）对应的能量Ecr的差值绝对值作为节点状态裕度指标：

节点能量与电压和无功注入间的相互关系反映了节点自身运行状态的变化趋势。由式（4），将节点i的能量Ei对电压幅值Ui的一阶偏导作为趋势指标：

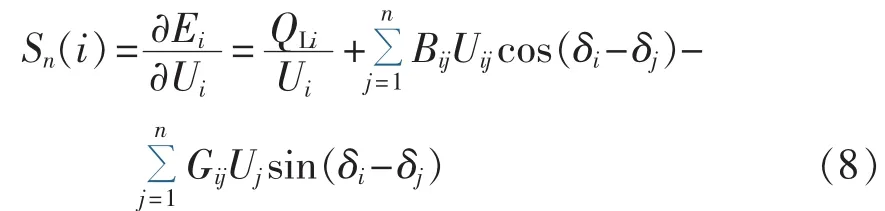
当Sn（i）≥0时，说明当前电压水平尚能承担此时的传输任务，节点鲁棒性较强；当 Sn（i）<0时，则节点能量随节点电压降低上升，脆弱趋势较为明显。当Sn（i）值越小时，说明节点对负荷增长的耐受能力越弱，表现出更为明显的脆弱趋势。因此Sn（i）可以借此找出对系统扰动反映灵敏的节点，物理意义明确。

由上述，状态脆弱性应综合考量灵敏度与裕度2个指标，于是定义以下状态脆弱性指标因子：

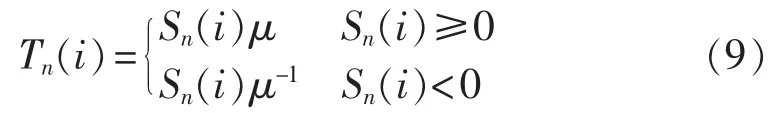
修正后的状态脆弱性指标值越小，表明相对而言更易受外界扰动的影响，鲁棒性较弱，节点电压更容易接近其极限崩溃点，表现出更强的脆弱性，若不采取及时的措施，可能达到电压临界值而导致系统崩溃；反之状态脆弱性指标越大，表明相对而言其更能抵御外界的干扰影响，表现出了较强的鲁棒性，脆弱性表现较弱。

2.2 结构脆弱性指标

由上述电气介数的概念和物理意义，将式（5）中βi定义为节点的结构脆弱性评估指标。

该值反映出了全网不同节点间潮流传输对节点的占用情况，量化了节点在全网中的潮流传输。该指标越大，表明其在全网潮流传输中越活跃，在拓扑结构上的重要程度更高。

2.3 改进后节点综合脆弱性评估指标

近些年来，国内外研究发展成果往往没能准确有效地兼顾实时状态参数与自身结构固有特性。传统的综合脆弱性指标如下：

采用上述指标对各标准系统及实际系统的仿真分析表明，所提节点综合脆弱性评估指标存在各因子对综合脆弱性的影响效应及比重考量中的不合理性和盲目性问题。实际电力系统运行中，系统运行过程中的故障情况大部分是由于外界的扰动造成的短时过电压、过电流现象，主要受到状态作用影响。然而当系统绝大部分系统节点固有电压水平较高时，元件的综合脆弱度更应与其在网络中的重要程度联系起来考量。单纯地将状态与结构两方面线性计算与实际系统运行情况不符。

因此在综合脆弱性指标中，状态与结构指标应该采取不同的权重因子进行评估，但式（10）未能考虑权重的影响。

针对上述指标的不合理性，在对状态与结构指标进行归一化处理后，提出改进后的基于节点电压水平的综合脆弱性评估指标：

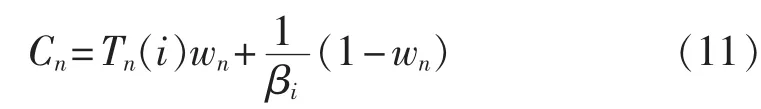
其中，Tn（i）、βi分别为节点状态脆弱因子和结构脆弱因子；wn为节点在不同电压水平下对应的不同权重因子。

对 IEEE30、IEEE57、IEEE118节点标准系统及实际系统仿真分析，基于改进后的综合脆弱性评估方法，采用逐步减小区间差值的逼近方法，对得到的脆弱性指标曲线进行最优选取，并进行分析验证，定义了节点在不同电压水平下的权重因子wn如表1所示，其中Um是实际电压值与基准电压值的比值。

新的综合脆弱性指标将系统的潮流分布及电压幅值统一到能量框架下，科学地结合灵敏度与裕度两方面，将元件自身运行状态、固有拓扑结构以及预想扰动与故障冲击影响量化。其不再是仅仅将状态与结构两者简单线性考虑，而是兼顾元件自身与系统其他部分的相互影响，多角度考察特定电气参数或拓扑参数对系统整体运行的作用，使综合脆弱性评估结果进一步贴近工程实际。

表1 不同电压水平对应的权重因子Table1 Weight factor for different voltage levels

3 算法仿真

3.1 算法流程

a.根据式（4）建立节点静态能量函数模型；

b.利用牛顿-拉夫逊潮流算法计算初始负荷下的系统潮流分布；

c.由式（4）、（7）、（8），运用连续潮流法 CPF（Continuation Power Flow method）计算不同负荷增长率情况下的节点状态脆弱性指标；

d.根据式（5），基于IEEE 30节点系统自身固有拓扑结构参数计算各个节点的结构脆弱性指标；

e.根据式（11）计算各节点在不同运行条件下的综合脆弱性指标；

f.对综合脆弱性指标大小进行排序；

g.进一步将本文综合脆弱性指标与传统线性相乘方法仿真结果进行对比分析。

3.2 状态脆弱性指标分析

分析基于IEEE 30节点系统结构与运行数据。考虑到实际电网中的负荷增长情况，分别选取负荷水平为λ=0、λ=0.1、λ=0.2这3种情况进行对比分析，分别代表负荷为基态水平、负荷增加10%、负荷增加20%这3种负荷模式。除了基态外，另取2种负荷增长模式的目的是分析电网中可能的负荷变化对系统运行状态变化趋势的影响。

从整体分析，随着负荷水平的增大，节点状态脆弱因子数值整体呈现减小趋势，由以上理论分析可知其状态脆弱性程度也有一定的加深，脆弱节点范围扩大。因为伴随着负荷的增长系统能量变化灵敏度相对增加，而节点能量裕度也进一步减小，系统鲁棒性减弱，抵御外界干扰能力下降，表现出逐渐增强的脆弱性。

具体分析可知，节点2、3、4在不同的负荷水平下均表现出了较其他节点更为明显的脆弱性，由IEEE 30节点系统分析，这几个节点是系统中主要的几个等效发电机及附近变压器，承担着向整个电网注入电能的任务，当负荷发生变化时，这些节点需立即增加出力和传输以维持系统潮流平衡，因此能量变化较大，对系统扰动反应灵敏，在整体电压水平均较正常的情况下表现出比其他节点更明显的脆弱趋势；节点6在负荷增长时脆弱程度明显加深，体现了其状态脆弱性受负荷增长的影响也较其他节点更为敏感。

为更清晰表现出各节点状态脆弱性指标及其受负荷增长影响，绘制节点状态脆弱因子分布曲线如图1—3所示。

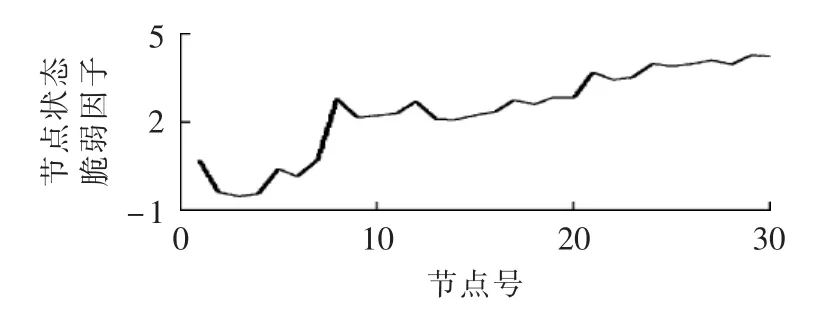
图1 λ=0时节点状态脆弱因子曲线Fig.1 Nodal conditional vulnerability factor curve when λ=0

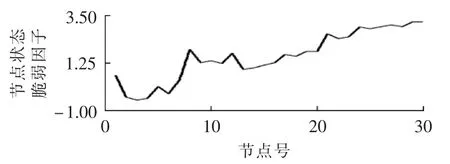
图2 λ=0.1时节点状态脆弱因子曲线Fig.2 Nodal conditional vulnerability factor curve when λ=0.1

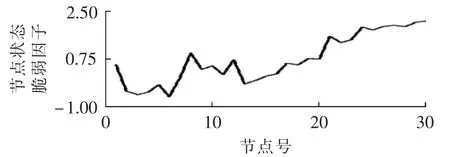
图3 λ=0.2时节点状态脆弱因子曲线Fig.3 Nodal conditional vulnerability factor curve when λ=0.2

3.3 结构脆弱性指标分析

根据系统固有元件对系统脆弱性的影响，将30节点的电气介数数据作图如图4所示。结构脆弱因子综合考虑所有发电和负荷节点的权重，将节点在全网潮流传输中的贡献量化，有效反映了节点的承载能力及其在网络中的活跃程度。

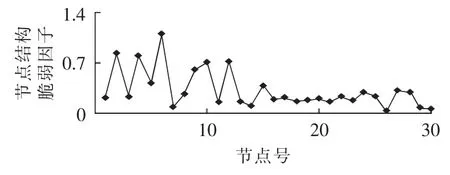
图4 结构脆弱因子曲线Fig.4 Nodal structural vulnerability factor curve

由图4所示节点结构脆弱因子曲线图可得出，节点6表现了较为突出的重要性。分析IEEE 30节点系统图，节点6靠近2个变压器支路，为主干变压器支路节点，若发生故障或退出运行，将导致发电机节点5、8功率无法向中部负荷传输，此时若系统不采取切负荷措施，将造成全网潮流大幅转移，给其他部分的节点和支路迅速、大幅加重负担，大量支路将因过载而退出运行，最终将导致灾难性电网事故的发生，因此它们的结构上表现出非常显著的脆弱性；节点2则是重要的发电机节点，直接担负功率注入的任务，若此节点退出运行，全网负荷供应将受到较大影响，并将导致系统内潮流无法平衡而出现崩溃现象。

3.4 综合脆弱性指标分析

由上述综合脆弱性计算改进方法得出更为贴近实际的综合脆弱度指标，如图5—7所示。

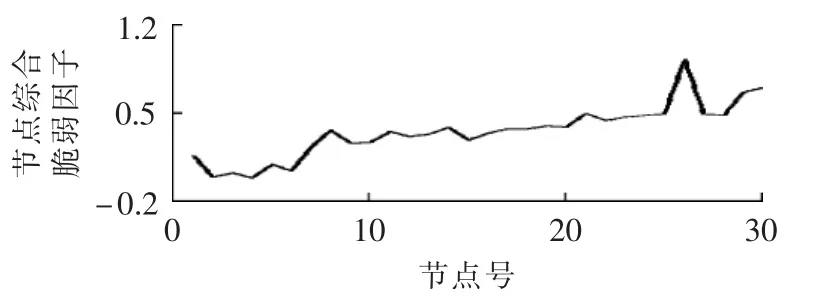
图5 λ=0时节点综合脆弱因子曲线Fig.5 Nodal comprehensive vulnerability factor curve when λ=0

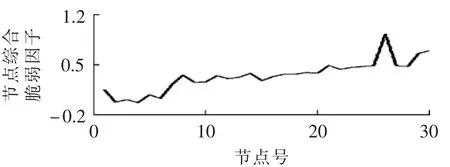
图6 λ=0.1时节点综合脆弱因子曲线Fig.6 Nodal comprehensive vulnerability factor curve when λ=0.1

图7 λ=0.2时节点综合脆弱因子曲线Fig.7 Nodal comprehensive vulnerability factor curve when λ=0.2

综合脆弱因子指标值越小，表征该节点不仅在运行状态上比其他节点对电网扰动的反应更为灵敏，同时其在网络拓扑结构中的重要程度也很高，若该节点受到扰动或发生故障退出运行，对系统其他部分的影响更大，节点综合脆弱性更显著。

节点6综合脆弱性表现较强。其电气介数数值上较大，而状态脆弱性表现在基态负荷下虽然没有那么强烈，但其受负荷增长影响较大，当负荷增长到20%时，其脆弱性表现达到最强，变化较为明显，也体现了状态因子对综合脆弱度的修正作用；节点4在不同负荷水平下均表现出了较强的综合脆弱性，是整个电网的主要功率来源，当负荷发生变化时，这些节点需立即增加出力和传输以维持系统潮流平衡，因此比其他节点更容易受系统扰动影响；结构上，节点4是发电机节点2的唯一直接相连的负荷节点，承担着区域间的电能传输的关键职能，表现出较高的重要度；节点26随着负荷的增长，综合脆弱性数值居高不下，表现出了较强的鲁棒性，分析IEEE 30节点系统图可知其位于系统末端节点，且有无功补偿装置，受外界扰动影响较小，退出运行对潮流分布的负面作用较弱。

3.5 对比论证

将本文的权重因子改进方法与文献［18］中传统的线性综合性评估方法进行比较分析，以进一步论证本文方法的合理性与优越性。以IEEE 30节点系统在基态负荷水平为例进行对比，2种方法脆弱节点排序如表2所示。

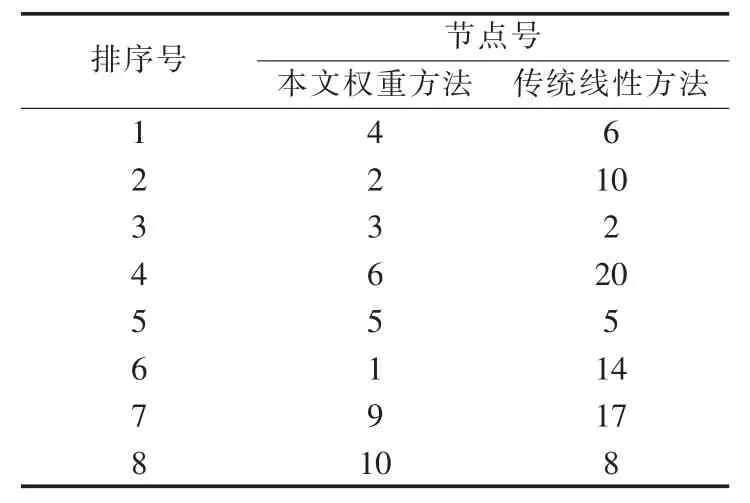
表2 2种方法对比Table 2 Comparison between two methods

对比2种方法的结果并结合IEEE 30节点系统图分析可知，本文方法所评估出的脆弱节点大多是发电机节点或承担重要传输任务的联络节点，此类节点受网络潮流变动影响较大，同时对负荷变化也更为敏感，且在潮流传输中贡献值更大，故易表现出强于其他节点的脆弱性。而传统方法评估的脆弱节点大多只是单纯状态脆弱性排序靠前，而未与结构重要度有效地结合［19-20］。可见，未考虑权重因子的综合脆弱性评估更易受运行状态主导影响，造成了脆弱节点一定程度上的误分类，与实际情况不符。

4 结论

本文改进了静态能量函数在状态脆弱性指标计算中的应用，并将变化率与裕度结合起来进行考虑，使其更加符合实际电力系统运行规律。在综合脆弱性指标的构建中，引入权重因子，既兼顾了状态与结构两方面的共同作用，又使其有所侧重与突出，结果更贴近生产实际。根据仿真分析结果得到如下结论。

a.对状态脆弱性的分析综合考量变化率与裕度2个因素的作用，并剥离了对系统影响相对较弱且对分析有负面效应的有功及相角，使状态脆弱性指标更为完善。

b.本文所采用的综合脆弱度指标不仅考虑运行状态与系统固有结构之间的互补作用，而且在此基础上量化了两者对综合脆弱性的贡献值，使指标结果更贴近实际。

c.较之于其他脆弱性评估方法，本文提出的方法更为全面，物理意义上更为清晰，综合考虑了多个量对结构的共同影响作用，更为准确地反映了系统中的脆弱节点。

d.本文所提指标基于基本的静态潮流，可在实际系统潮流计算中得到，方法便捷，思路清晰，静态能量函数模型计算速度较快，有望应用于工程生产实践中。所得的脆弱性指标可直观地进行定量分析，有助于工作人员高效地筛选出系统脆弱环节并判断脆弱程度。

［1］GERAR D L D，KJETIL U，GERD H K，etal.Vulnerability analysis of the Nordic power system［J］.IEEE Transactions on Power Systems，2006，21（1）：402-410.

［2］YU Xingbin.A practical approach for integrated power system vulnerability analysis with protection failures［J］.IEEE Transactions on Power Systems，2004，19（4）：1811-1820.

［3］魏震波，刘俊勇，朱国俊，等.电力系统脆弱性理论研究［J］.电力自动化设备，2009，29（7）：38-43.WEIZhenbo，LIU Junyong，ZHU Guojun，etal.Powersystem vulnerability［J］.Electric Power Automation Equipment，2009，29（7）：38-43.

［4］白加林，刘天琪，曹国云，等.电力系统脆弱性评估方法综述［J］.电网技术，2008，32（2）：26-30.BAI Jialin，LIU Tianqi，CAO Guoyun，et al.A survey on vulnerability assessment method for power system［J］.Power System Technology，2008，32（2）：26-30.

［5］赵莹莹，赵洪山.电网脆弱性评估方法［J］.山东电力技术，2009（5）：21-27.ZHAO Yingying，ZHAO Hongshan.Vulnerability assessment of power systems［J］.Shandong Dianli Jishu，2009（5）：21-27.

［6］刘耀年，术茜，禹冰，等.基于电气介数的电力系统脆弱性分析［J］. 电测与仪表，2011，48（7）：61-64.LIU Yaonian，SHU Xi，YU Bing，et al.Analysis of power system vulnerability based on electrical betweenness［J］.Electrical Measurement and Instrumentation，2011，48（7）：61-64.

［7］徐政勋，张伟民.电网脆弱性分析的一种新方法［J］.电力系统保护与控制，2014，42（12）：87-90.XU Zhengxun，ZHANG Weimin.A new method of power system vulnerability analysis［J］.Power System Protection and Control，2014，42（12）：87-90.

［8］周彦衡，吴俊勇，张广韬，等.考虑级联故障的电力系统脆弱性评估［J］. 电网技术，2013，37（2）：444-449.ZHOU Yanheng，WU Junyong，ZHANG Guangtao，et al.Assessment on power system vulnerability considering cascading failure［J］.Power System Technology，2013，37（2）：444-449.

［9］张虹，田雨青.基于电流介数的电力系统脆弱性评估［J］.电测与仪表，2014，51（12）：40-43.ZHANG Hong，TIAN Yuqing.Vulnerability assessment in the power system based on the current betweenness［J］.Electrical Measurement and Instrumentation，2014，51（12）：40-43.

［10］张国华，张建华，杨京燕，等.基于有向权重图和复杂网络理论的大型电力系统脆弱性评估［J］.电力自动化设备，2009，29（4）：21-26.ZHANG Guohua，ZHANG Jianhua，YANG Jingyan，et al.Vulnerability assessmentofbulk powergrid based on weighted directionalgraph and complex network theory［J］.Electric Power Automation Equipment，2009，29（4）：21-26.

［11］卢锦玲，朱永利.基于暂态能量裕度的电力系统脆弱性评估［J］.电工技术学报，2010，25（6）：96-103.LU Jinling，ZHU Yongli.Power system vulnerability assessment based on transient energy margin［J］.Transactions of China Electrotechnical Society，2010，25（6）：96-103.

［12］刘群英，刘俊勇，刘起方.基于支路势能信息的电网脆弱性评估［J］. 电力系统自动化，2008，32（10）：6-11.LIU Qunying，LIU Junyong，LIU Qifang.Power grid vulnerability assessment based on branch potential energy information ［J］.Automation of Electric Power Systems，2008，32（10）：6-11.

［13］卢锦玲，姬群星，朱永利.基于能量函数法的电网脆弱性评估［J］. 电网技术，2008，32（7）：30-33.LU Jinling，JI Qunxing，ZHU Yongli.Power grid vulnerability assessment based on energy function［J］.Power System Technology，2008，32（7）：30-33.

［14］曹一家，陈晓刚，孙可.基于复杂网络理论的大型电力系统脆弱线路辨识［J］. 电力自动化设备，2007，26（12）：1-5.CAO Yijia，CHEN Xiaogang，SUN Ke.Identification of vulnerable linesin powerfrid based on complex network theory ［J］.Electric Power Automation Equipment，2007，26（12）：1-5.

［15］陈卓，李华强，周柯宇，等.考虑风电场影响的电力系统支路脆弱性评估［J］. 电力系统及其自动化学报，2014，26（2）：37-43.CHEN Zhuo，LI Huaqiang，ZHOU Keyu，et al.Vulnerable branch assessment of power system considering wind farm effects［J］.Proceedings of the CSU-EPSA，2014，26（2）：37-43.

［16］黄昭蒙，李华强，杜涛，等.基于支路能量函数的脆弱支路评估［J］. 电力系统保护与控制，2012，40（15）：7-11.HUANG Zhaomeng，LIHuaqiang，DU Tao，etal.Vulnerable branch assessment based on branch energy function［J］.Power System Protection and Control，2012，40（15）：7-11.

［17］徐林，王秀丽，王锡凡.电气介数及其在电力系统关键线路识别中的应用［J］. 中国电机工程学报，2010，30（1）：33-39.XU Lin，WANG Xiuli，WANG Xifan.Electic betweenness and its application in vulnerable line identification in power system［J］.Proceedings of the CSEE，2010，30（1）：33-39.

［18］徐行，李华强，赵祥云，等.基于运行状态和网络结构的节点综合脆弱性评估［J］. 电网技术，2014，38（3）：731-735.XU Hang，LI Huaqiang，ZHAO Xiangyun，et al.Assessment on nodal comprehensive vulnerability based on operational state and network structure［J］.Power System Technology，2014，38（3）：731-735.

［19］雷成，刘俊勇，魏震波，等.计及网络传导能力与抗干扰能力的节点综合脆弱评估模型［J］. 电力自动化设备，2014，34（7）：144-149.LEI Cheng，LIU Junyong，WEI Zhenbo，et al.Integrative evaluation model of node vulnerability considering network transmission ability and anti-interference ability［J］.Electric Power Automation Equipment，2014，34（7）：144-149.

［20］李扬，苏慧玲.N-k故障下影响电力系统脆弱性的关键线路研究［J］. 电力自动化设备，2015，35（3）：60-67.LI Yang，SU Huiling.Critical line affecting power system vulnerability under N-k contingency condition［J］.Electric Power Automation Equipment，2015，35（3）：60-67.