Oscillation Criteria for Third-order Nonlinear Neutral Dynamic Equations on Time Scales∗

ZHANG Zhi-yu,HAN Qiang,YU Yuan-hong

(1-Department of Science,Taiyuan Institute of Technology,Taiyuan 030008;2-School of Mathematics,Shandong University,Jinan 250100;3-Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190)

1 Introduction

In this paper,we will study the oscillation and asymptotic behavior for third-order nonlinear neutral delay dynamic equation on time scaleT:

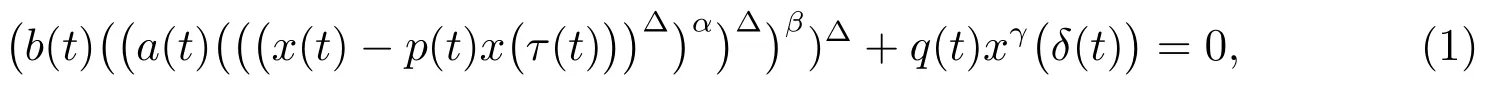
whereand sup

In order to study the above equation,we assume that the following assumptions are satisfied.

(A1):whereAandBare odd positive integers;

(A2):a(t),b(t),p(t)andq(t)are positive real-valued rd-continuous functions Defined onT→R,satisfying both

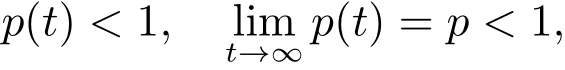
and

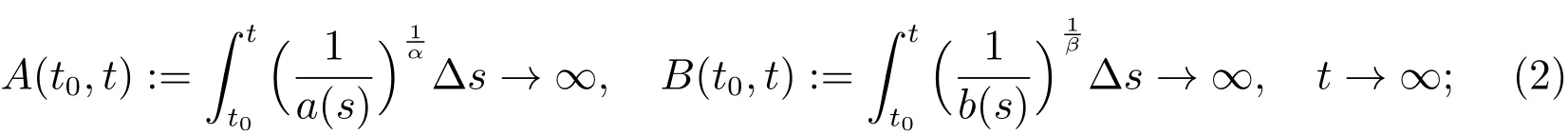
(A3):τ(t)andδ(t)are real-valued rd-continuous functions defined onT→R,satisfying both:

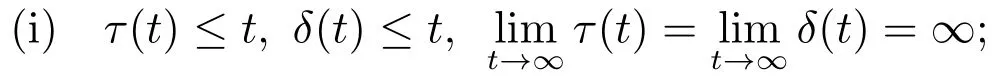
(ii)There exists a family ofsatisfying

Recently there is an increasing interest in the study of oscillation for nonlinear dynamic equations on time scales[1-14],because many practical problems,such as those from electronic engineering,mechanical engineering,ecological engineering,aerospace engineering and so on,need to be described by them.For examples,Keller studied an electrical oscillatorcircuit with resistanceR,inductanceL,and capacitanceC.Suppose the capacitor is discharged periodically every time unit and assume that the discharging takesδ＞0(but small)time units.Then this simulation can be modeled using the time scale

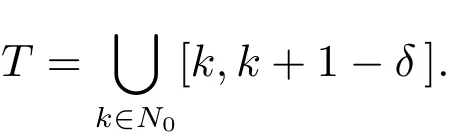
IfQ(t)is the total charge on the capacitor at timetandI(t)is the current as a function of timet,then we have

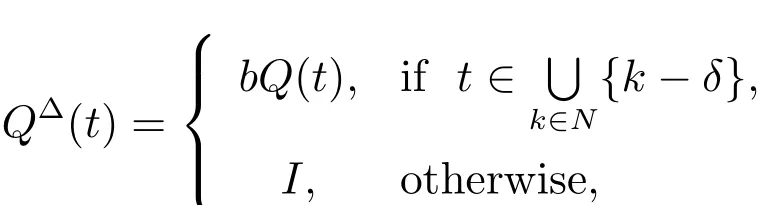
and

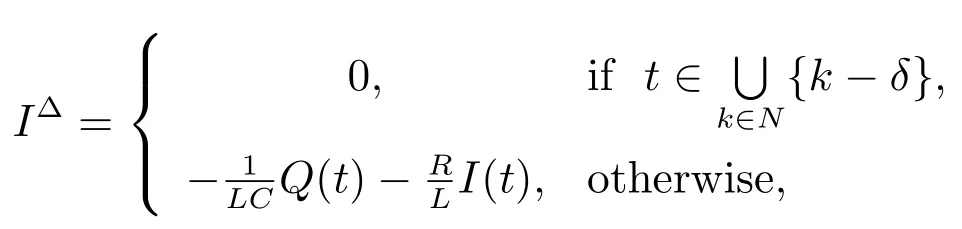
wherebis a constant satisfyingErbeet al[4,5]studied the oscillation for third-order dynamic equations on time scales

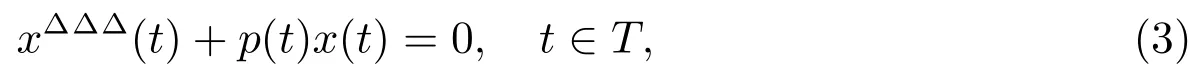
and

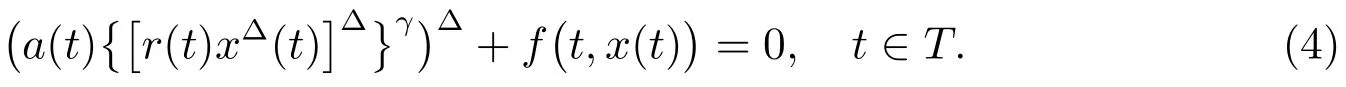
Liet al[6]studied the oscillation and asymptotic behavior for third-order semi-linear delay dynamic equations on time scales with the following form

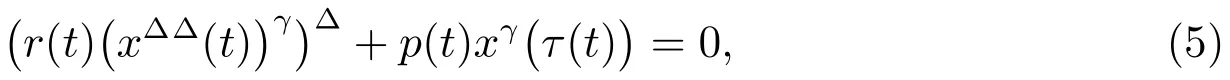
whereAandBdenote non-negative odd numbers.Their work improves the existing conclusions.Hanet al[7]obtained every solutionx(t)of the following equation is either oscillatory or

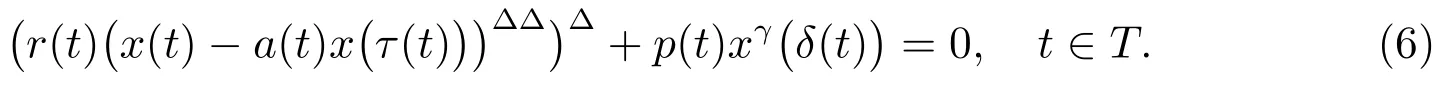
Yu and Wang[8]studied the oscillation and asymptotic behavior of third-order nonlinear dynamic equations on time scales

However,we wonder whether their results still hold under the more general conditionsp(t)＞0 andα,β/=1.To the best of our knowledge,there are few results about(1)under the case ofp(t)＞0 andα,β/=1.By using Riccati transformation technique,some new sufficient conditions are obtained in this paper to ensure every solutionx(t)of(1)is either oscillatory or

This paper is organized as follows.In section 2,some basic definitions and lemmas are given.In section 3,we discuss the oscillation and asymptotic behavior for thirdorder non-linear neutral delay dynamic equation(1)on time scales.

2 Some preliminary results

In this section,in order to obtain our main oscillatory and asymptotic behavior results for(1),some basic Definitions[1]and lemmas are listed below.

Definition 1A time scale is an arbitrary non-empty closed subset of the real numbers.

Throughout this paper we will denote a time scale by the symbolT.We assume that a time scaleThas the topology that it inherits from the real numbers with the standard topology.

Definition 2Fort∈Twe define the forward jump operatorbywhile the backward jump operatorsupIfwe say thattis right-scattered,while ifwe say thattis left-scattered.

In this definition,we put infhas a maximumt)and supifThas a minimumt),where∅ denotes the empty set.

Definition 3A point is called isolated if it is right-scattered and left-scattered.Also,ift＜supTandσ(t)=t,thentis called right-dense,and ift＞infTandρ(t)=tthentis called left-dense.Points that are right-dense and left-dense at the same time are called dense.Finally,the graininess functionis defined by

Definition 4A functionis called regulated provided its right-sided limits exist(finite)at all right-dense points inTand its left-sided limits exist(finite)at all left-dense point inT.A functionis called rd-continuous provided it is continuous at right-dense points inTand its left-sided limits exist(finite)at left-dense points inT.

We also need the setTκwhich is derived from the time scaleTas follow:ifThas a left-scattered maximumm,thenOtherwise,In summary

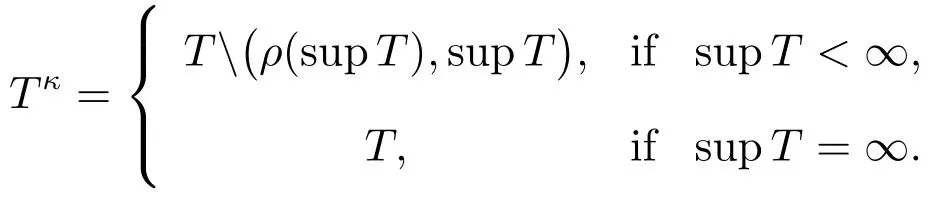
Definition 5Assumeis a function and letthen we defineto be the number(provided it exists)with the property that given anythere is a neighborhoodoftsuch that

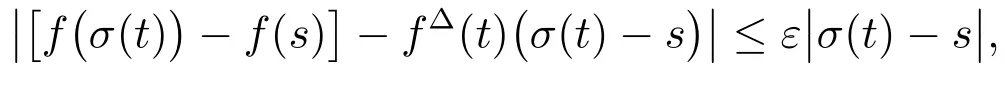
for alls∈U.We callthe delta derivative offatt,andfis delta differentiable att.

From the definition ofwe can obviously get:

(ii)is the usual forward difference operator if

Definition 6A functionis called an antiderivative ofprovidedholds for allWe define definite integral of functionfromatobby

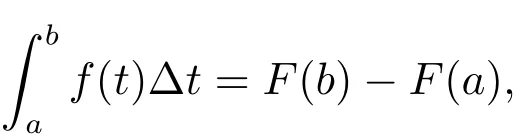
whereF(t)is an antiderivative off(t),and we call the functionf(t)is integrable on

The set of rd-continuous functionswill be denoted in this paper byThe set of functionsthat are delta differentiable and whose delta derivative is rd-continuous is denoted bySimilarly the set of functionsthat are second order delta differentiable and whose second order delta derivative is rd-continuous is denoted by

Lemma 1[1]Assume thatare delta differentiable atThen:

(i)The sumis delta differentiable attwith

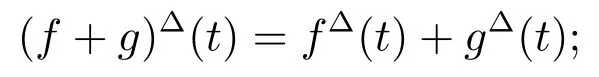
(ii)For any constant c,is delta differentiable attwith

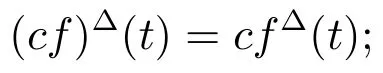
(iii)The productis delta differentiable attwith

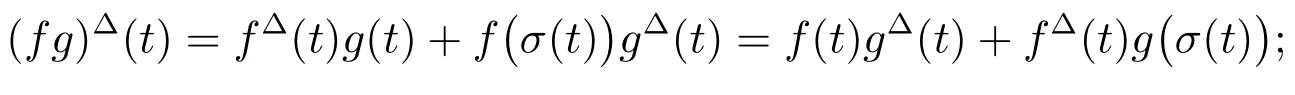
(iv)Ifthenis delta differentiable attwith

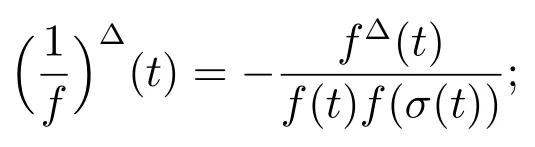
(v)Ifthenis delta differentiable attand

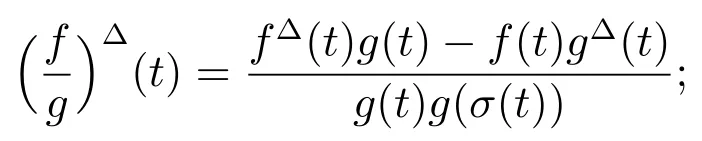
(vi)(Keller chain rule)Assume that functionis continuous differentiable and functionis delta differentiable.Then the composite functionis delta differentiable,and

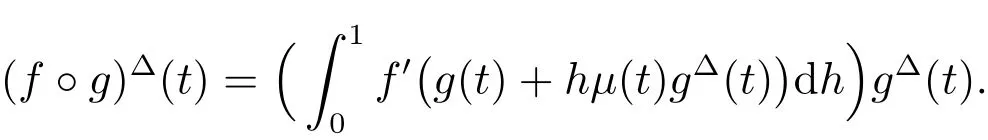
Throughout the paper,the following notation will be used

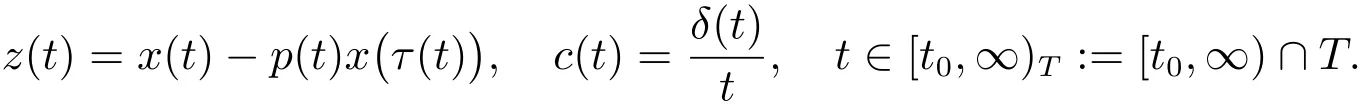
Lemma 2Assume thatx(t)is an eventually positive solution of(1)satisfying(A3)and(2)for all sufficiently largeThenz(t)satisfies either:

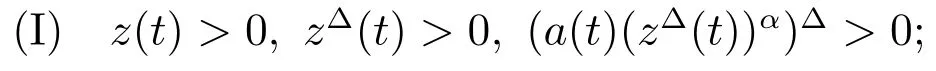
or

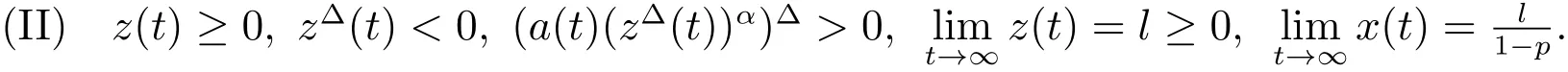
ProofSincex(t)is an eventually positive solution of(1).There exists asuch thatandBy(A3)and(1),we have

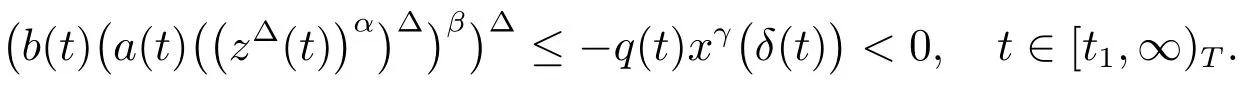
This impliesis decreasing on,andis eventually either positive or negative.Furthermore,We claim thatotherwise,suppose that there isonfor some givenThusis decreasing and there exists a negative constantdsuch that

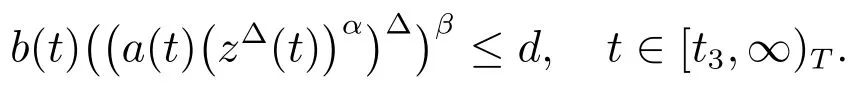
Dividing the above equation byb(t)and integrating it fromWe get

We obtainifin(8).Therefore,there exists a constantcand asuch that

onDividing the above equation bya(t)and integrating it fromt4tot.We get

which impliesin(9).Sincewe can choose a constantp0satisfyingThen there exists aλ＞0 such that

By(A3),there exists a positive integerk0satisfyingck＞t5for any sufficiently largekonThus

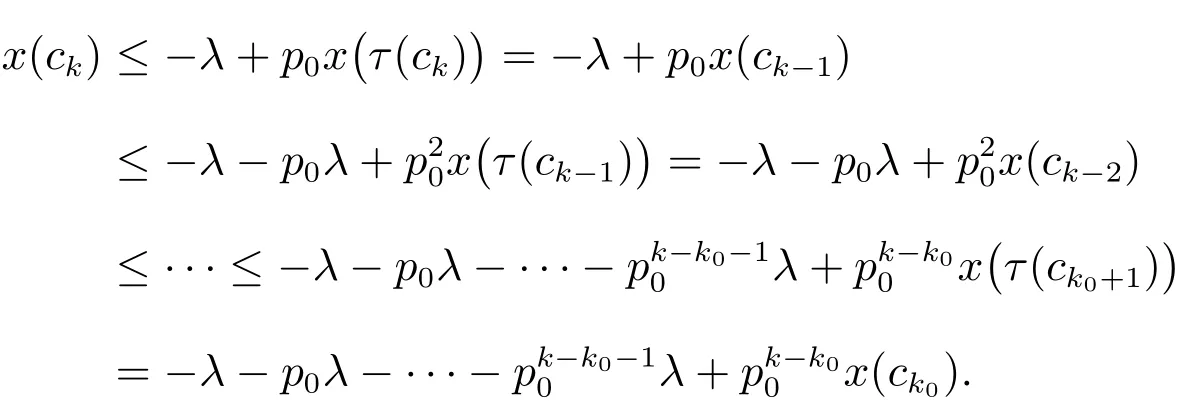
It contradicts withx(t)＞0.Hence

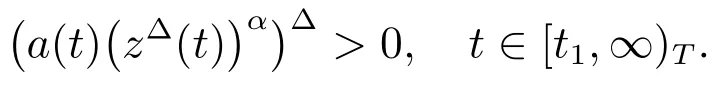
This implies thator

Ifby Keller chain rule,we conclude

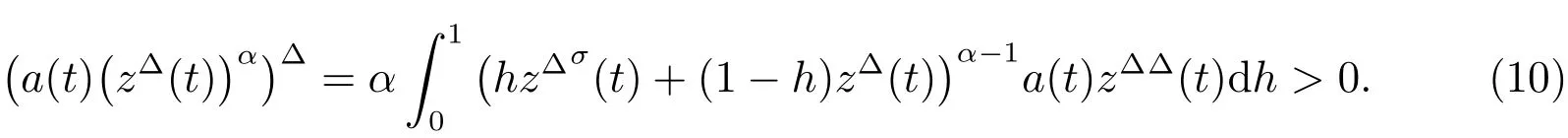
Therefore,Furthermore,

Ifwe getfrom(10).Furthermore,Otherwise,orFrom(A3),there exists aandsuch thatThen

which impliesBy the definition ofz(t),we haveThis contradictsorHence,we haveandlis a finite number.We claim thatx(t)is a bounded solution.Otherwise,there exists asatisfyingsuch that

Givenwe have

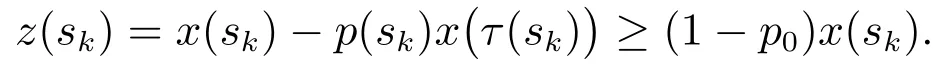
ThusThis contradictsAssume that

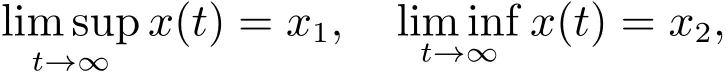
whereBy 0≤p＜1,we concluDeThis implies thatIt is clear that

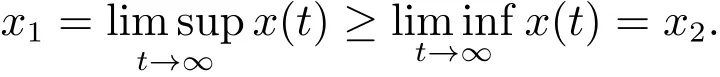
Hencex1=x2.Consequently,The proof is completed.

Lemma 3Assume thatx(t)is an eventually positive solution of(1)and satisfies the property(I)of Lemma 2.Then there exists asuch that

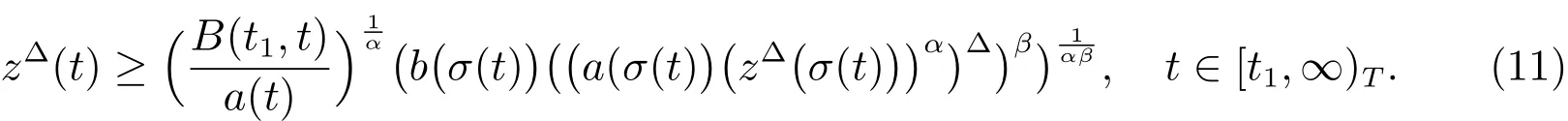
ProofAccording to(1),there exists aand asuch that

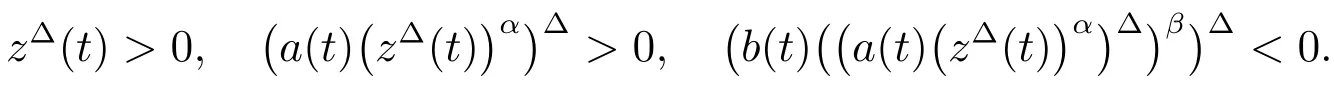
This implies thatis decreasing onFurthermore

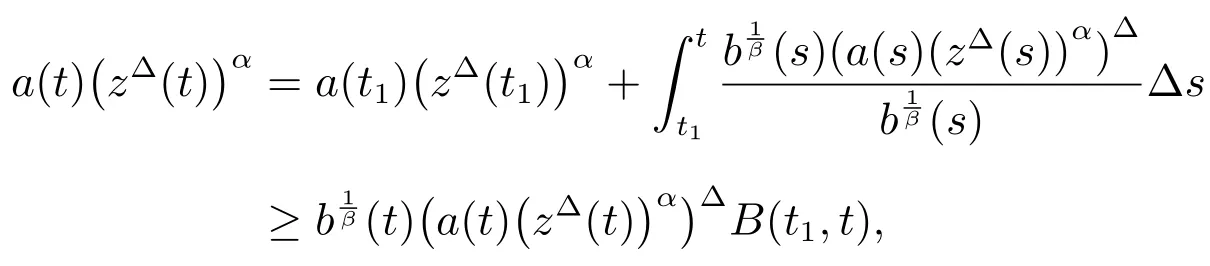
consequently

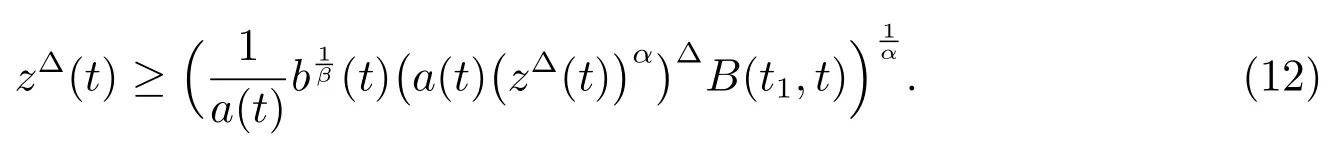
Sinceis decreasing onwe obtain

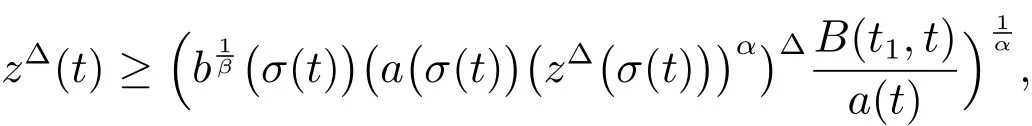
and(11).The proof is completed.

Lemma 4Assume thatx(t)is an eventually positive solution of(1)and satifies the property(I)of Lemma 2.If

then there exists asuch that

Thusis strictly decreasing on

ProofDefine.Thus

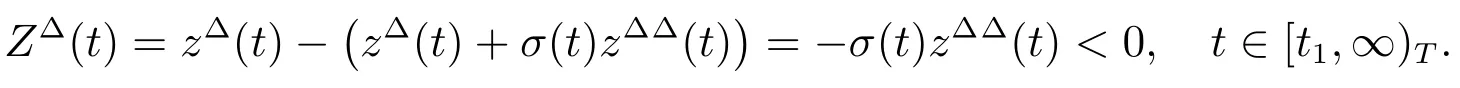
We claim thatZ(t)＞0 eventually.Otherwise,onwhen

Then

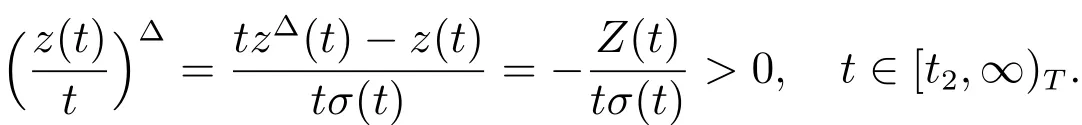
Which implies thatis strictly increasing onWe claim that there exists asuch thatand

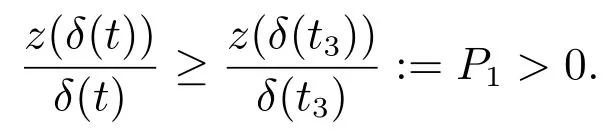
By the definition ofz(t),we getFrom(A3)and(1),we obtain

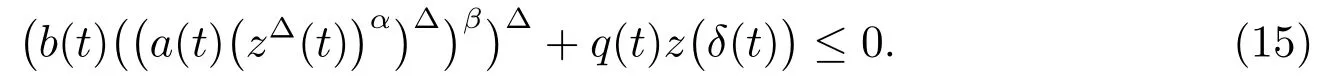
Integrating(15)fromt3tot,we have

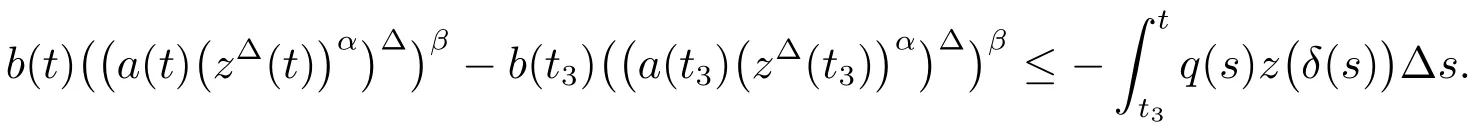
Which yields that

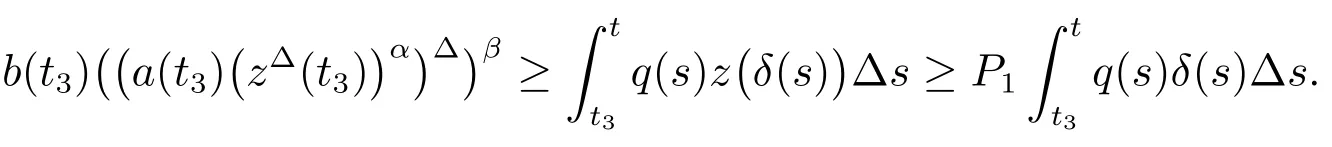
Which contradicts(13).Henceandis strictly decreasing onThe proof is completed.

Lemma 5Assume thatx(t)is an eventually positive solution of(1)and satisfies the property(II)of Lemma 2.If

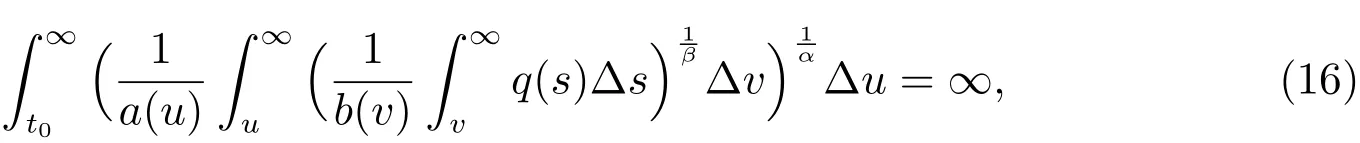
then

ProofIt is clearNext we claim thatl=0.Otherwise,there exists asuch thatfor allBy the definition ofz(t),we get(15).Integrating(15)fromtto∞,we obtain

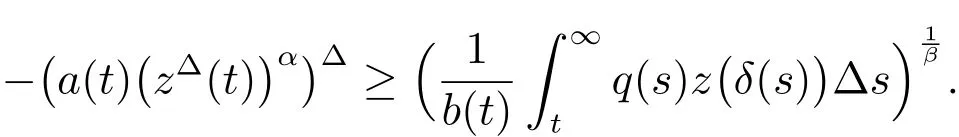
Integrating again fromtto∞,we obtain

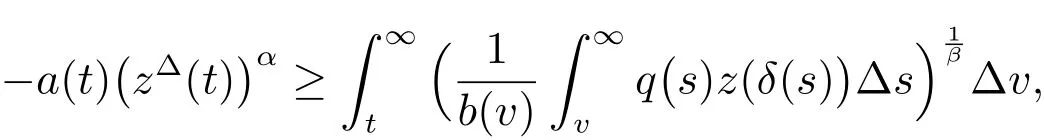
that is

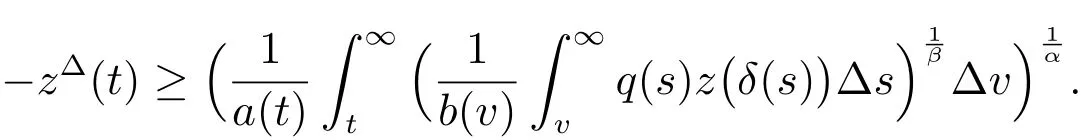
Integrating again fromt0to∞,we have

Which contradicts(16).HenceThe proof is completed.

3 Main results

Theorem 1Assume that(A3),(2),(13),(16)and1 hold.Suppose that there exists a positive functionsuch that for anyc＞0

holds,then every solutionx(t)of(1)is either oscillatory or

ProofSuppose thatx(t)is a nonoscillatory solution of(1).Without loss of generality,there exists asuch thatonThe proof is similar to Lemma 2 ifx(t)is an eventually negative solution.By Lemma 2,z(t)satisfies property(I)or(II)of Lemma 2.Assumez(t)satisfies property(I)of Lemma 2.Define the functionωby

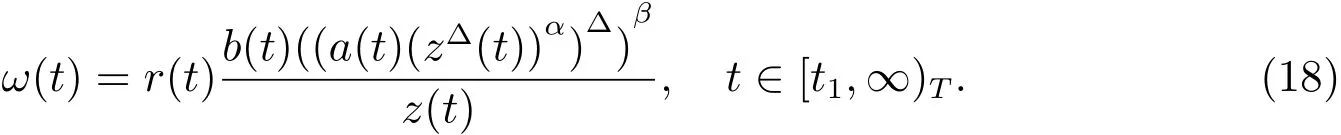
This impliesω(t)＞0.Using the product rule,we get

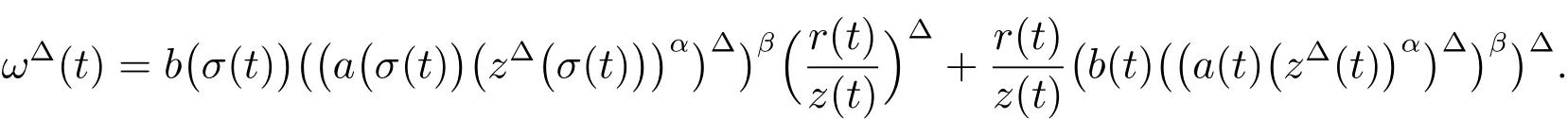
By quotient rule and(15),we obtain

From(18),we get

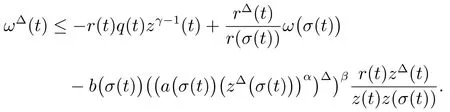
Sinceis decreasing onthere exists a constant 1such that

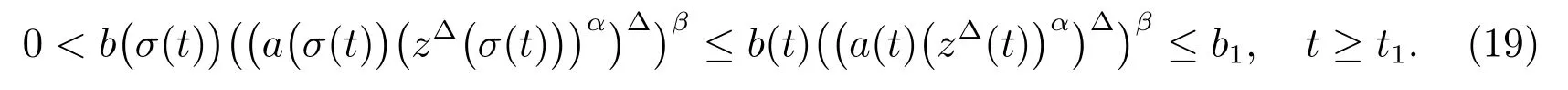
Substituting(19)into(11),we have

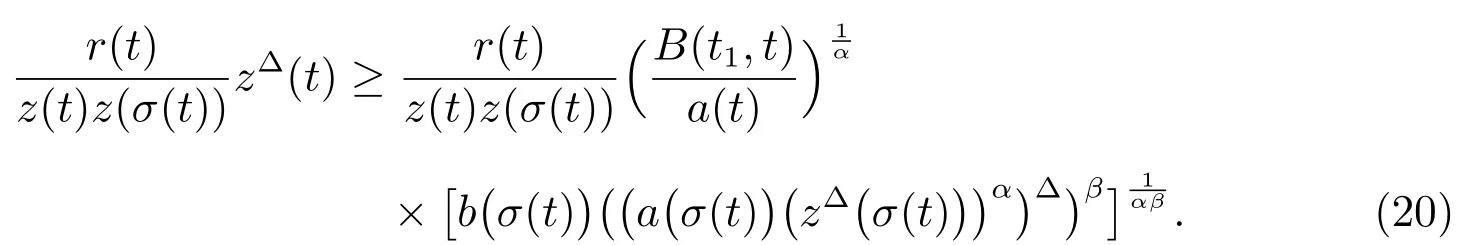
From(18),(19),andthere exists a constantc＞0,such that

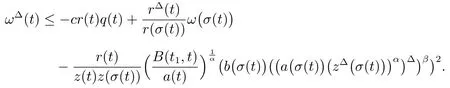
Sinceand with the help of(14),we obtain

From(20)and(21),we get

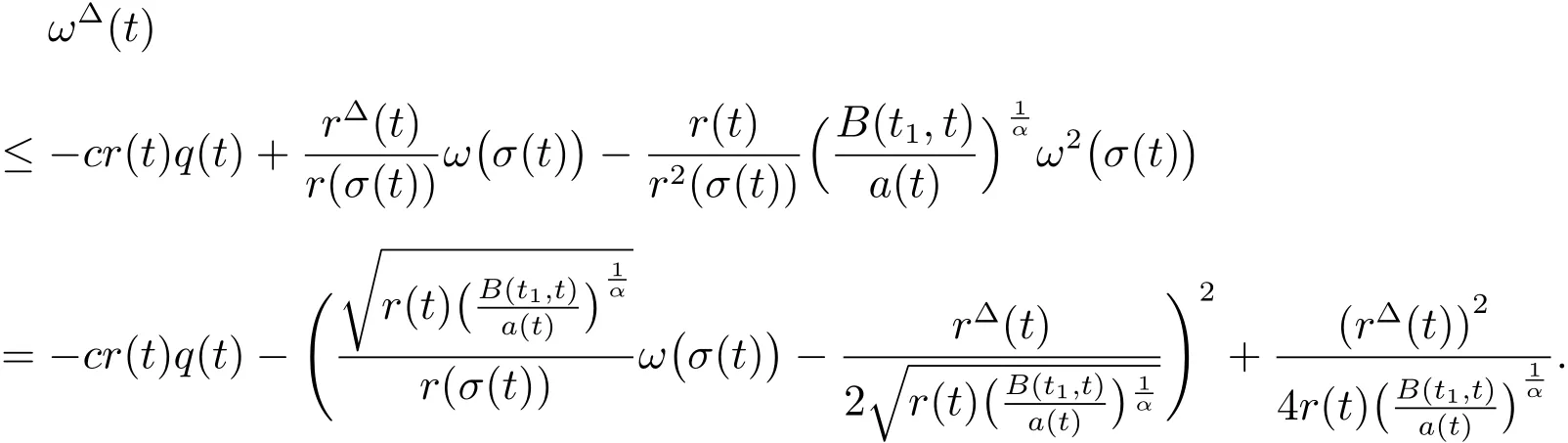
Hence

Integrating(22)fromt1tot,we have

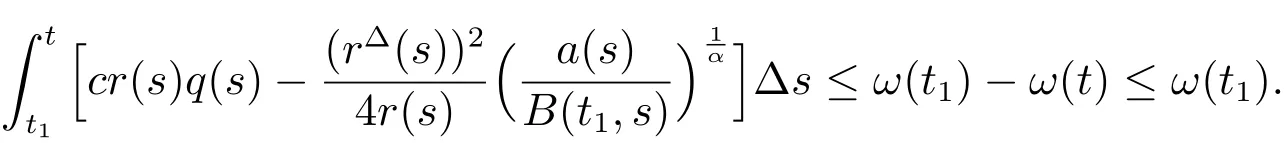
Which contradicts(17).By Lemma 5,we geteventually if the property (II) of Lemma 2 holds.The proof is completed.

Corollary 1Assume that(A3),(2),(16)andhold.If

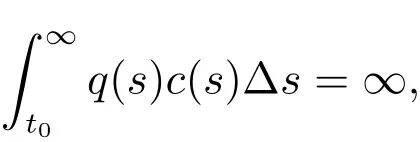
then every solutionx(t)of(1)is either oscillatory or

Corollary 2Assume that(A3),(2),(13),(16)and1 hold.If

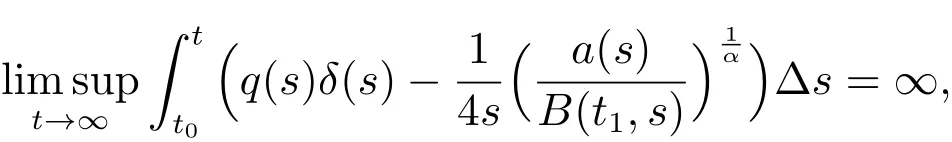
then every solutionx(t)of(1)is either oscillatory or

Theorem 2Assume that(A3),(2),(13),(16)andhold.Furthermore,assume that there exists a positive functionsuch that for somem≥1 and for anyc＞0,

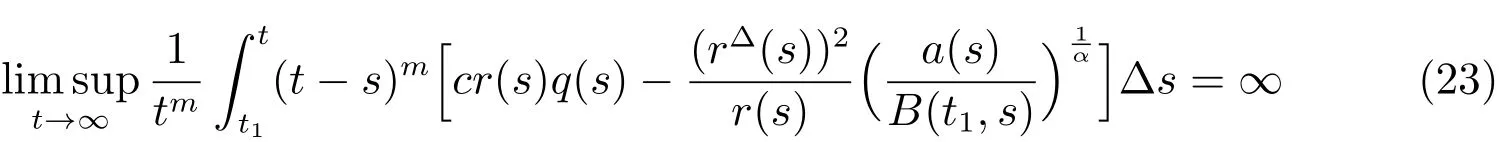
holds,then every solutionx(t)of(1)is either oscillatory or

ProofSuppose thatx(t)is a nonoscillatory solution of(1).Without loss of generality,there exists asuch thatonBy Lemma 2,z(t)satisfies property(I)or(II)of Lemma 2.Ifz(t)satisfies property(I)of Lemma 2.It is clear that(22)holds by Theorem 1.Multiplying(22)byand integrating it fromt1tot,we get

furthermore

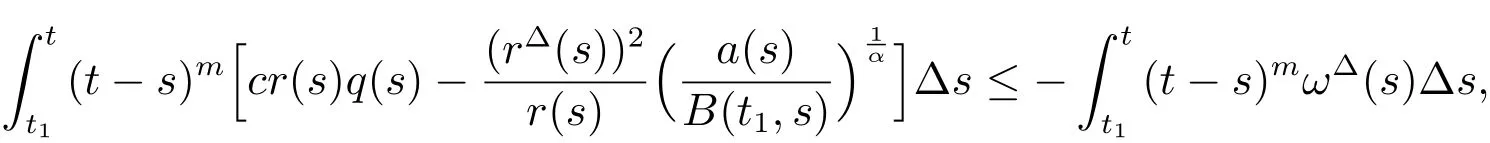
whereω(t)is defined as in(18).The rest proof is similar as in Theorem 1,which contradicts(23).By Lemma 5,we obtaineventually if property(II)of Lemma 2 holds.The proof is completed.

Based on Theorem 1 and Theorem 2,we prove two new Kamenev oscillation criteria for(1).Besides two new Philos oscillation criteria for(1)are given in Theorem 3 and Theorem 4.

Define

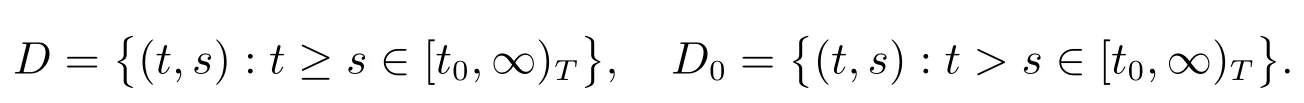
We conclude that a functionH:D→Rhas the property ofP,if it satisfies:

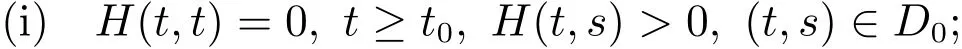
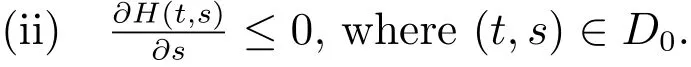
Theorem 3Assume that(A3),(2),(13),(16)andhold.Suppose that there exists a functionHwith propertyP,a functionand a functionsuch that for any

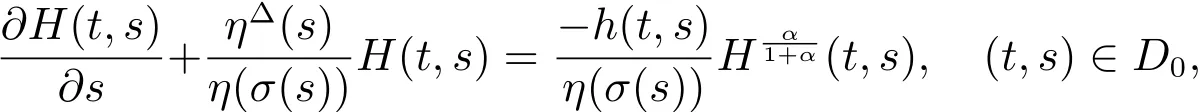
and

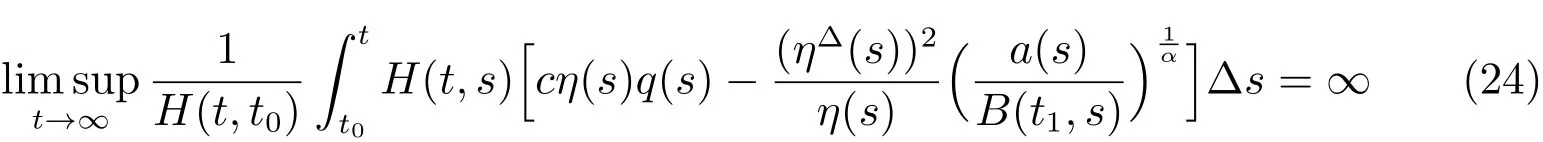
hold,then every solutionx(t)of(1)is either oscillatory or

ProofSuppose thatx(t)is a nonoscillatory solution of(1).Without loss of generality,there exists asuch thatonBy Lemma 2,we obtain thatz(t)satisfies property(I)or(II)of Lemma 2.It is clear that(22)holds by Theorem 1 ifz(t)satisfies property(I)of Lemma 2.Multiplying(22)byH(t,s) and integrating it fromt1tot,we obtain

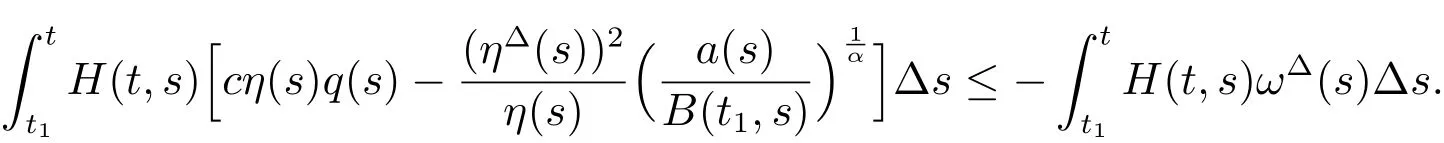
The rest proof is similar as in Theorem 2.This contradicts(24).The proof is completed.

Theorem 4Assume that(A3),(2),(13),(16)andαβ≤1 hold.If

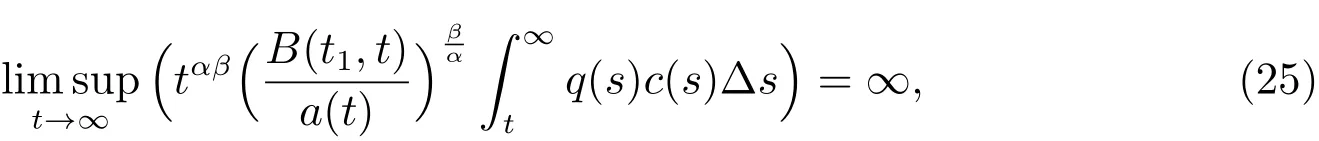
then every solutionx(t)of(1)is either oscillatory or

ProofSuppose thatx(t)is a nonoscillation solution of(1).Without loss of generality,there exists asuch thatonBy Lemma 2,z(t)satisfies property(I)or(II)of Lemma 2,then from(15)and for sufficiently largewe have

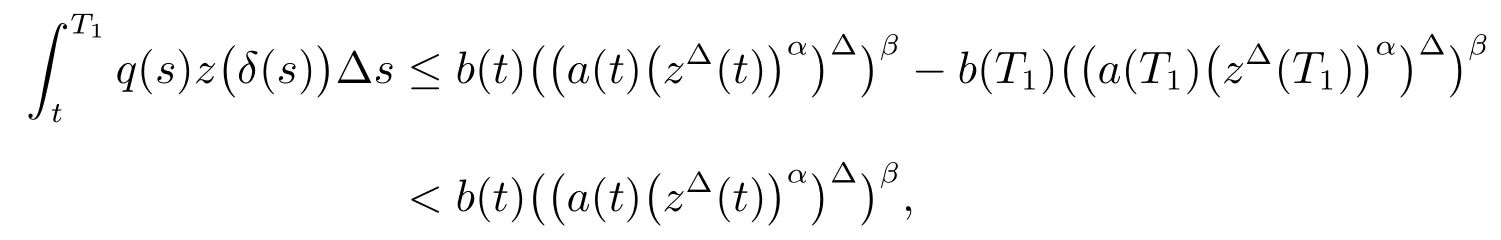
that is

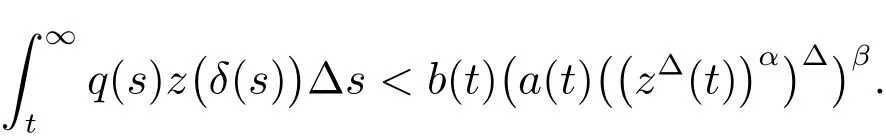
From(12),we get

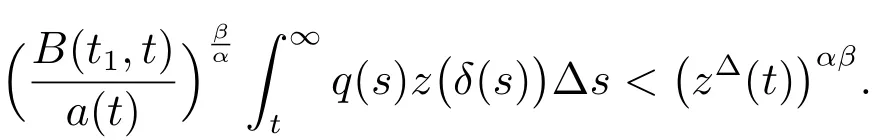
Fromand letwe obtain

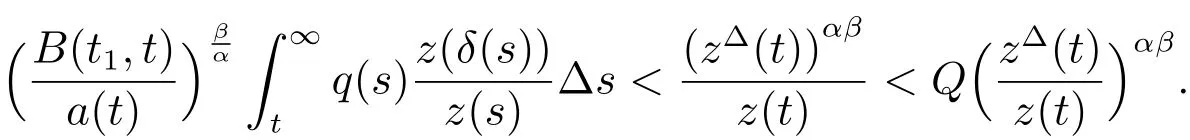
From(14),we have

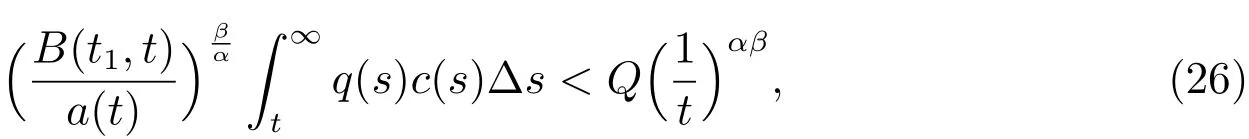
furthermore

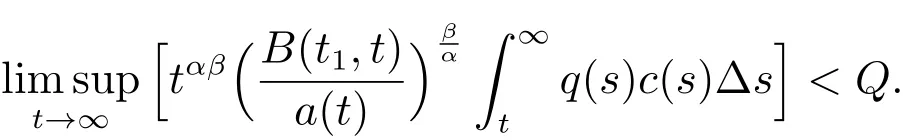
This contradicts(25).By Lemma 5,we can concludeif property(II) of Lemma 2 holds.The proof is completed.

Example 1Consider the third-order nonlinear equation on time scales

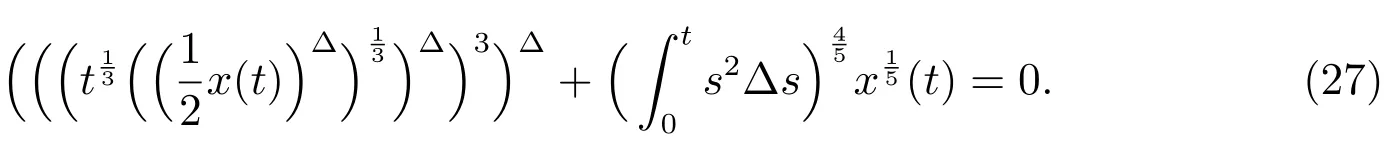
Here

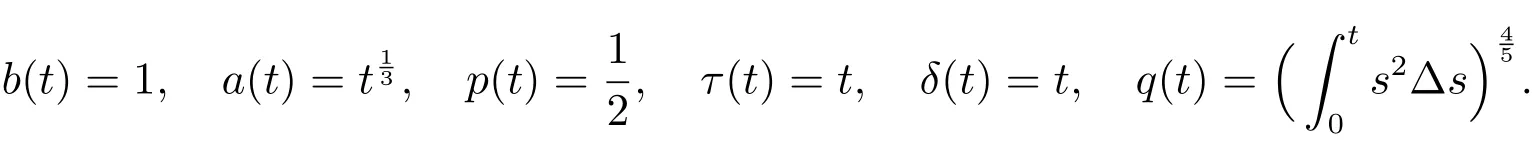
It is clear that(2),(13)and the(16)hold.By Theorem 2,it remains to prove(23)holds.Letm=1,r(t)=1.We have

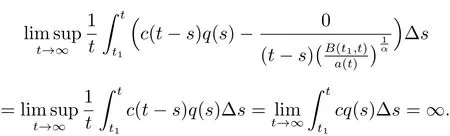
From Theorem 2,we claim that every solutionx(t)of(27)is either oscillatory or

This paper establishes some new Kamenev oscillation criteria and new Philos oscillation criteria.Theorem 1,Corollary 1,Corollary 2 and Theorem 2 establish some new Kamenev oscillation criteria;Theorem 3 and Theorem 4 establish some new Philos oscillation criteria.Lemma 2 generalizes Lemma 1[10];Lemma 5 generalizes Lemma 2[10];Theorem 1 generalizes Theorem 3.1.1[12];Theorem 2 generalizes Theorem 3.1.2[12];Theorem 3 generalizes Theorem 3[10]and Theorem 3.1.3[12].Furthermore,oscillation criteria in the papers[1–14]can not concluDeevery solution of(27)is either oscillatory or converge to zero.Therefore,theorems of this paper generalize the results in above papers.

References:

[1]Bohner M,Peterson A.Dynamic Equations on Time Scales,an Introduction with Applications[M].Boston:Birkhauser,2001

[2]Han Z L,Li T X,Sun S R,et al.Oscillation criteria for third order nonlinear delay dynamic equations on time scales[J].Annales Polonici Mathematici,2010,99(2):143-156

[3]Erbe L H,Peterson A C,Saker S H.Asymptotic behavior of solutions of a third-order nonlinear dynamic equations on time scales[J].Journal of Computational and Applied Mathematics,2005,181(1):92-102

[4]Erbe L H,Peterson A C,Saker S H.Hille and Nehari type criteria for third order dynamic equations[J].Journal of Mathematical Analysis and Applications,2007,329(1):112-131

[5]Erbe L H,Peterson A C,Saker S H.Oscillation and asymptotic behavior a third-order nonlinear dynamic equations[J].The Canadian Applied Mathematics Quarterly,2006,14(2):129-147

[6]Li T X,Han Z L,Sun Y B,et al.Asymptotic behavior of solutions for third-order half-linear delay dynamic equations on time scales[J].Journal of Applied Mathematics and Computing,2011,36(1):333-346

[7]Han Z L,Li T X,Sun S R,et al.Oscillation behavior of third-order neutral Emden-Fowler delay dynamic equations on time scales[J].Advances in Difference Equations,2010,2010(1):1-23

[8]Yu Z H,Wang Q R.Asymptotic behavior of solutions of third-order nonlinear dynamic equations on time scales[J].Journal of Computational and Applied Mathematics,2009,225(2):531-540

[9]Bohner M,Guseinov G S.Improper integrals on time scales[J].Dynamic Systems and Applications,2003,12(1-2):45-65

[10]Zhang Z Y,Wang X X,Yu Y H.Oscillation theorems for third-order neutral differential equations with distributed delay[J].Chinese Journal of Engineering Mathematics,2013,30(6):871-880

[11]Han Z L,Shi B,Sun S R.Oscillation of a class of second order delay dynamic equation on time scales[J].Journal of Shanghai Jiao Tong University,2007,41(10):1718-1721

[12]Sun Y B,Han Z L.Research on oscillation behaviour of delay dynamic equation[D].Jinan:University of Jinan,2012:33-43

[13]Zhang Q X,Gao L,Wang L.Oscillation of second-order nonlinear delay dynamic equations on time scales[J].Computers and Mathematics with Applications,2011,61(8):2342-2348

[14]Hassan T S.Oscillation criteria for half-linear dynamic equations on time scales[J].Journal of Mathematical Analysis and Applications,2008,345(2):176-185