一个具有时滞和阶段结构的比率依赖型捕食系统的稳定性∗

王玲书,张雅南,冯光辉

(1-河北经贸大学数学与统计学学院，石家庄 050061;2-军械工程学院基础部，石家庄 050003)

1 引言

捕食者–食饵(捕食)系统是种群动力学中一类非常重要的模型，已经被许多学者所研究.经典的Lotka-Volterra型捕食模型均假定，捕食者种群的平均捕食率只依赖于食饵种群的密度.近年来，在生物学和生理学中越来越多的证据表明：在许多情形下，特别是当捕食者不得不搜寻食物(因此不得不分享或竞争食物)时，一个更切合实际且更一般的捕食模型应基于“比率依赖”理论.粗略地讲，即捕食者种群的平均增长率应为食饵种群密度与捕食者种群密度之比的函数，这一理论已被大量的野外观察结果或实验室数据所证实[1,2].一般地，一个比率依赖型捕食系统具有下列形式

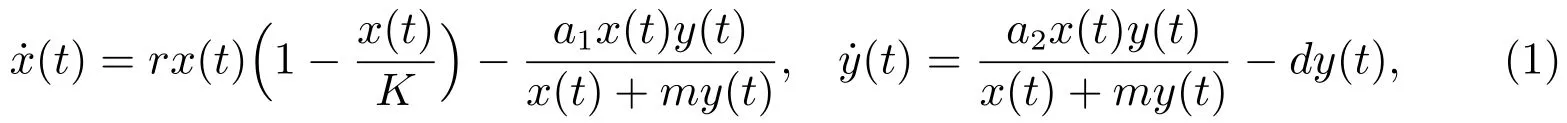
其中x(t)和y(t)分别表示食饵种群和捕食者种群在时刻t的密度.参数r,K,a1,a2,d和m均是正常数.Kuang和Beretta在文献[3]中系统地研究了系统(1)的边界平衡点和正平衡点的全局稳定性，得到了系统(1)持续生存的充分条件.在文献[4]中，Xu等在系统(1)的基础上，考虑了Holling-III型功能性反映函数及时滞的影响，讨论了下列系统的稳定性

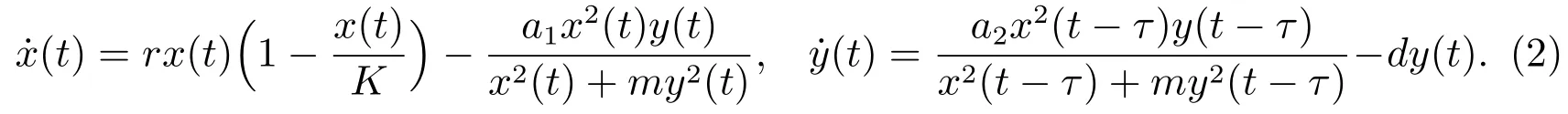
注意到在上述捕食系统中，人们总假定每个捕食者具有相同的捕食和生产能力，而每个食饵具有相同的受捕食者攻击的风险，这个假设对许多动物来说似乎是不切实际的.在自然界中，物种的增长常常有一个成长发育的过程，如从幼年到成年等，而且在其成长的每一个阶段都会表现出不同的特征.因此，考虑具有阶段结构的种群模型更具有实际意义.近年来，具有阶段结构的捕食模型引起了许多学者的兴趣[5-9].基于前面的讨论，本文分别将捕食者种群和食饵种群分成两个阶段：成年种群和幼年种群，并且假设仅有成年捕食者捕食成年食饵，并讨论由捕食者种群的孕期所引起的时滞对种群动力学性态的影响.为此，研究下列微分系统

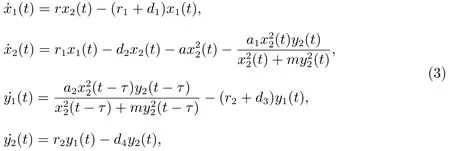
其中x1(t)和x2(t)分别表示幼年食饵和成年食饵在时刻t的密度，y1(t)和y2(t)分别表示幼年捕食者和成年捕食者在时刻t的密度.参数a,a1,a2,d1,d2,d3,d4,r,r1,r2和m均是正常数.τ≥0表示捕食者种群的妊娠时间.

本文讨论的系统(3)将基于以下初始条件

其中

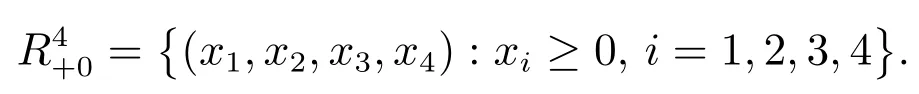
由泛函微分方程的基本理论[10]易知，系统(3)存在唯一满足初始条件(4)的解.易证系统(3)满足初始条件(4)的所有解在上有定义且保持恒正，本文将系统(3)满足初始条件(4)的解称为正解.

2 局部稳定性和Hopf分支

容易验证，当时，系统(3)存在一个边界平衡点

其中

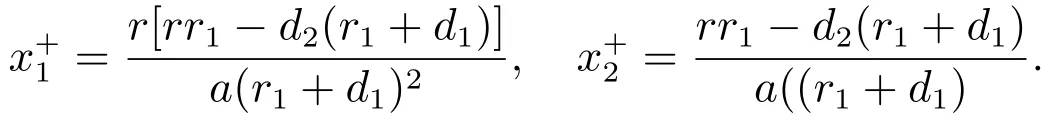
当下列条件成立时

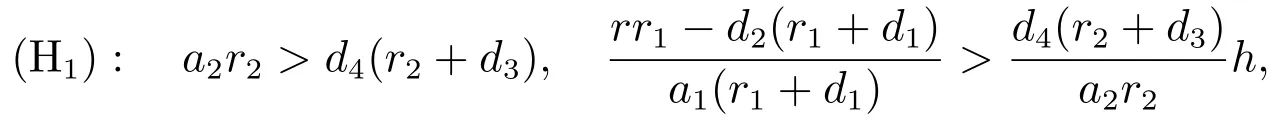
系统(3)存在一个正平衡点其中

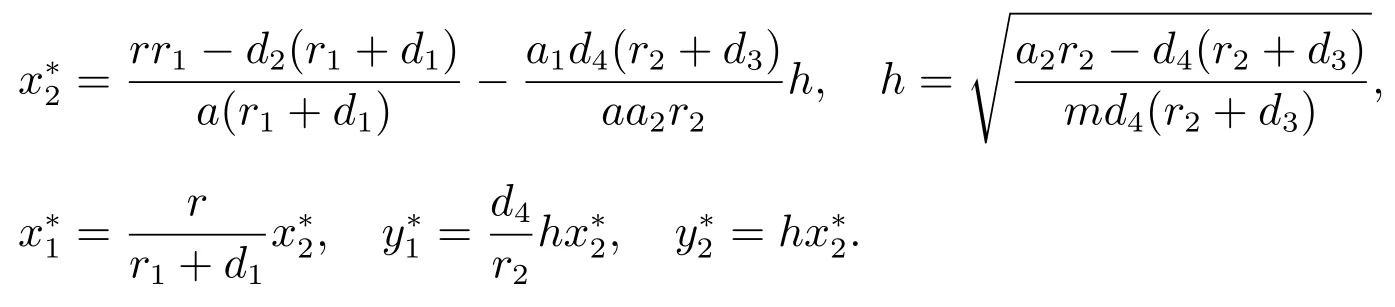
系统(3)在平衡点的特征方程为

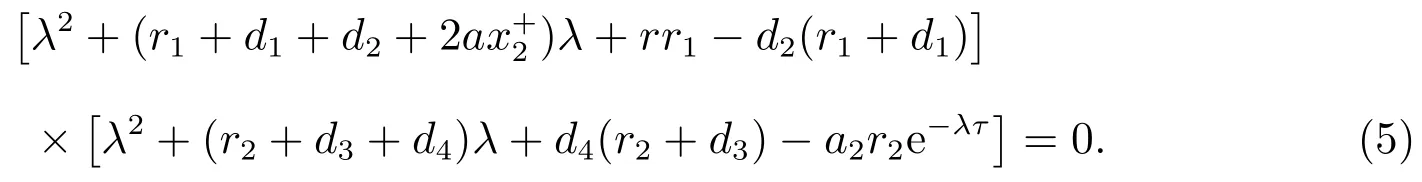
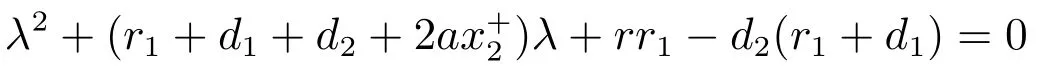
的两个根均是负的.因此方程(5)的其它根由

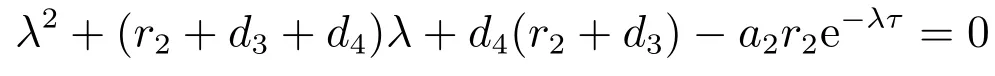
决定.令

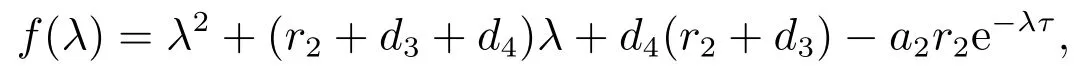
如果我们有

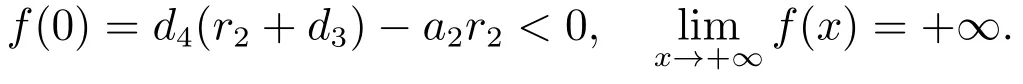
因此，f(λ)=0存在一个正实根，此时E1是不稳定的.如果直接计算可得

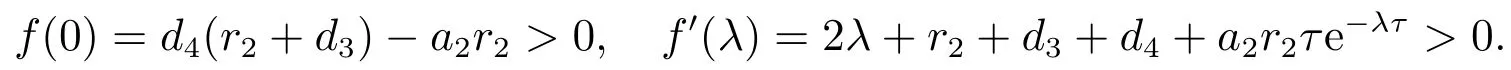
此时，E1是局部渐近稳定的.由文献[5]的引理B可以得到，对所有的τ＞0,E1是局部渐近稳定的.

系统(3)在平衡点处的特征方程为

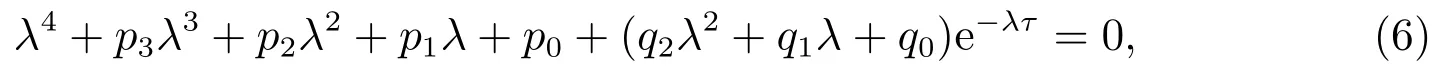
其中

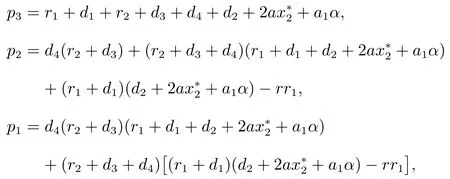
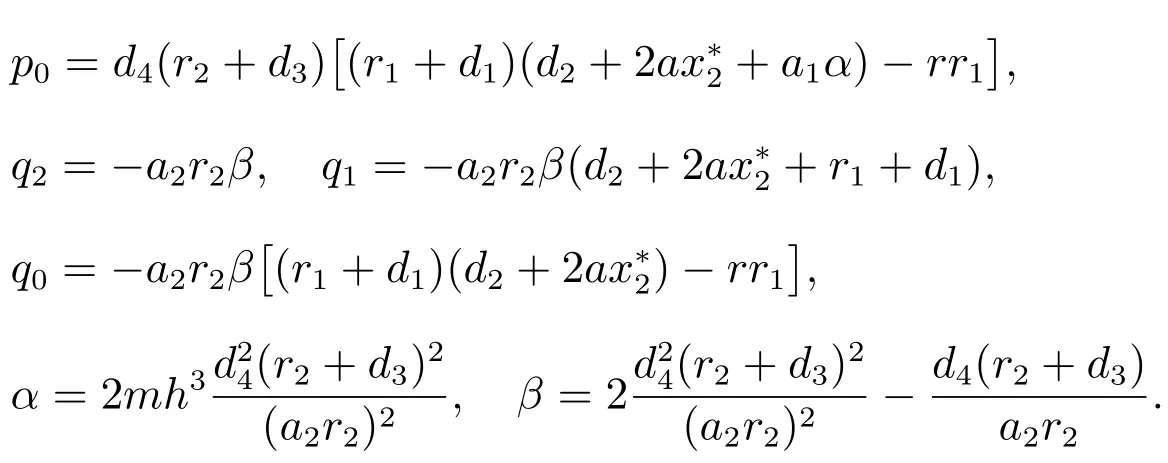
当τ=0时，方程(6)变为

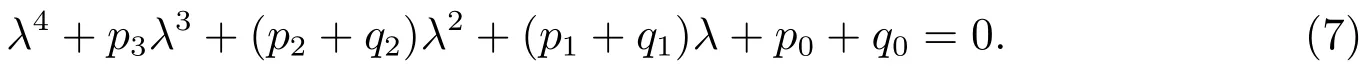
显然，p3＞0.当下列条件成立时

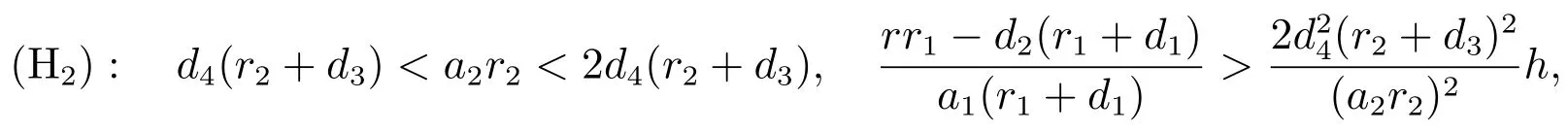
可以得到

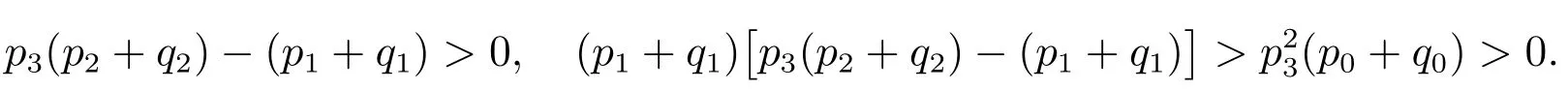
由Hurwitz判定定理可知，平衡点E∗是局部渐近稳定的.

如果iω(ω＞0)是方程(6)的解，可以验证ω满足下列方程

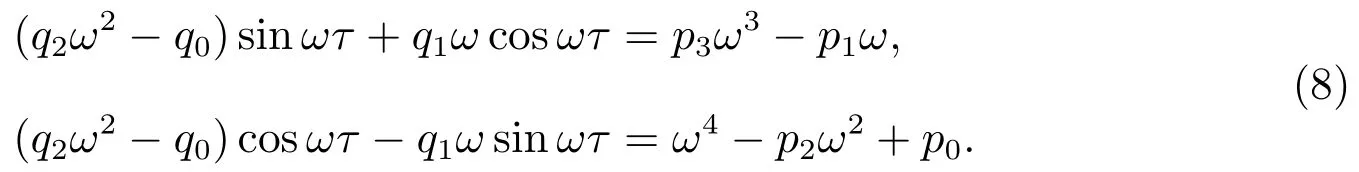
把方程(8)的等式两边平方相加，可得

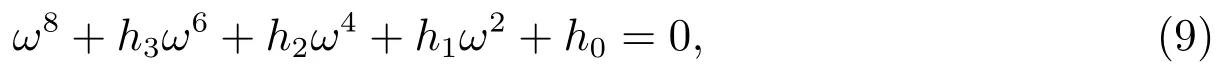
其中

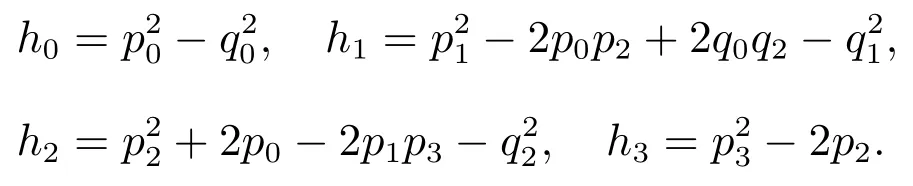
如果(H2)成立，直接计算可以得到

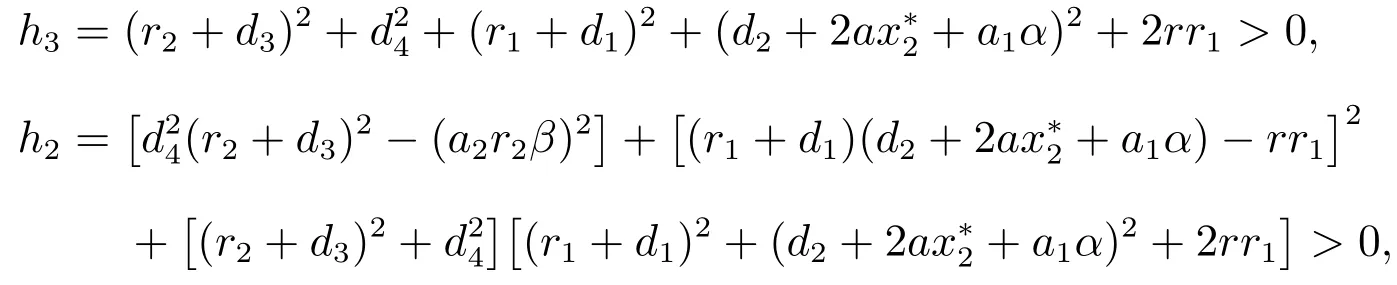
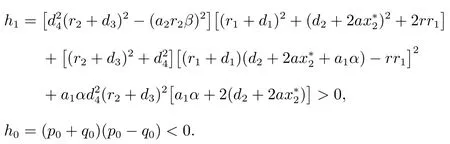
因此，方程(9)存在唯一的正实根ω0，即特征方程(6)存在一对共轭复数根由方程(8)，可以求得相应的τk，计算结果如下

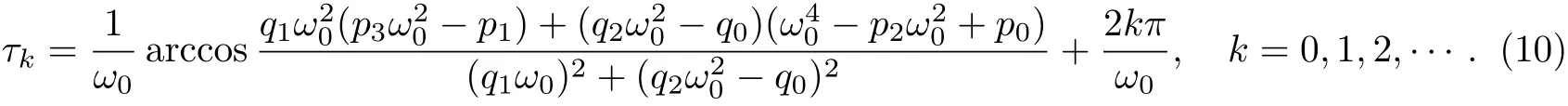
由文献[11]，可以得到当(H2)成立时，对是局部渐近稳定的.

现在证明下列横截条件

计算方程(6)关于τ的导数，可以得到

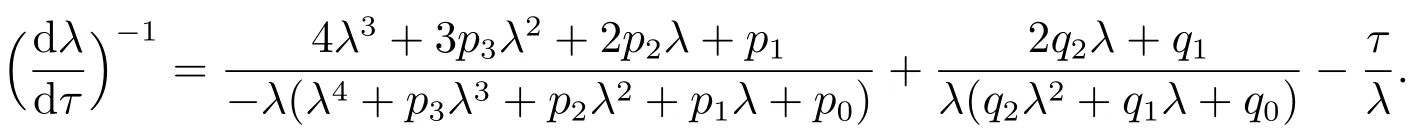
由此可以推出

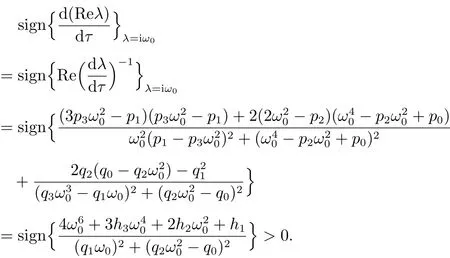
因此，横截条件(11)成立.由文献[10]可知当时，系统(3)存在一个Hopf分支.

综上所述，可以得出下列结论.

定理2.1对于系统(3)，有下列结论：

(i)假设当成立时，平衡点是局部渐近稳定的；当成立时，平衡点E1是不稳定的；

(ii)假设(H2)成立，则存在正常数τ0，使得当时，E∗是局部渐近稳定的，当τ＞τ0时，E∗是不稳定的，在τ=τ0处，系统(3)存在一个Hopf分支.

3 全局稳定性

本节我们将运用单调迭代方法和比较定理，讨论系统(3)的边界平衡点和正平衡点的全局稳定性.

定理3.1假设则当时，平衡点是全局渐近稳定的，即捕食者种群将走向灭绝.

证明 设为系统(3)满足初始条件(4)的任一正解.由系统(3)的第二个方程可得

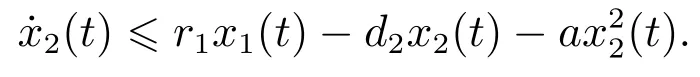
考虑辅助系统

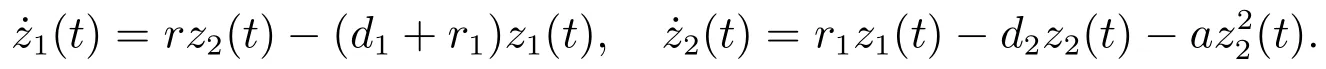
由文献[8]的引理2.2可知，当时

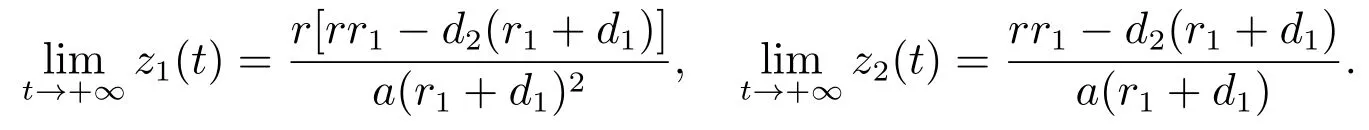
由比较定理可以得到

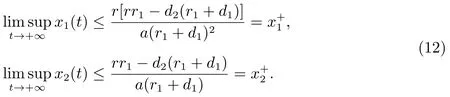
因此，对充分小的ε＞0，存在一个T1＞0，当t＞T1时，

对于t＞T1+τ，由系统(3)的第三个方程可得

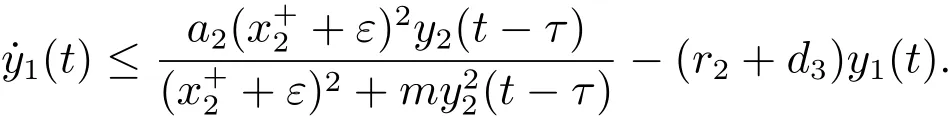
考虑辅助系统

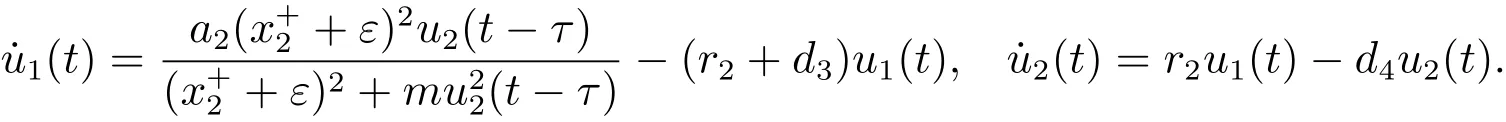
由文献[9]的引理2.4可知，当时

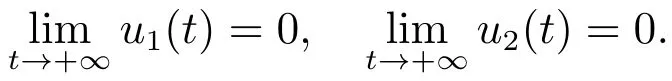
由比较定理可以知道

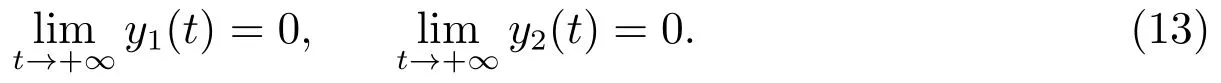
因此对充分小的ε＞0，存在一个T2＞T1，当t＞T2时，y2(t)＜ε.

对于t＞T2，由系统(3)的第二个方程可以得到

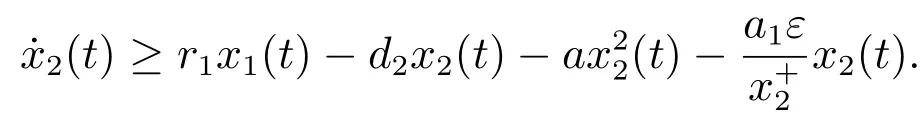
考虑辅助系统

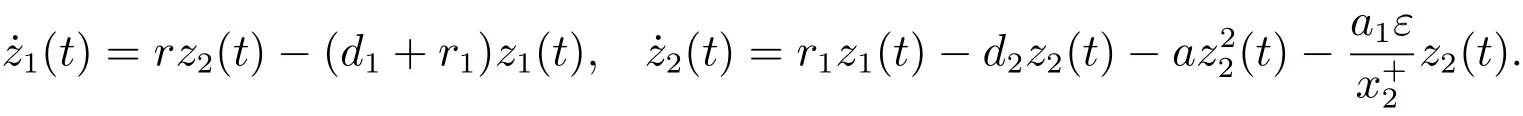
由文献[8]的引理2.2可知，当时

对充分小的ε＞0，由比较定理可以得到

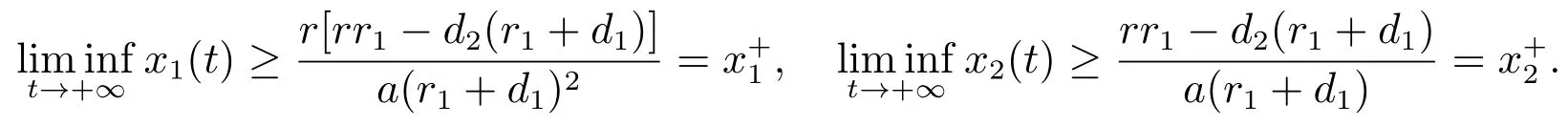
结合(12)和(13)可以得到

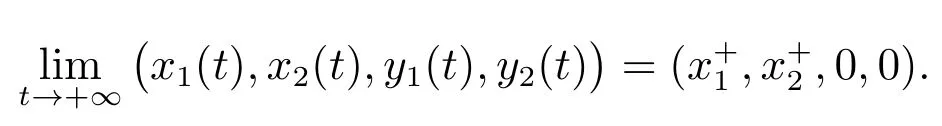
这样，我们就证明了当成立时，E1是全局渐近稳定的.

定理3.2设成立，若下列条件满足：

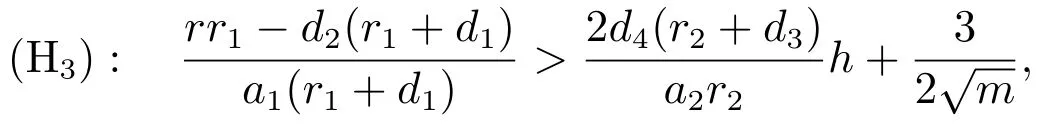
则系统(3)的平衡点是全局吸引的.

证明 设为系统(3)满足初始条件(4)的任一正解.令

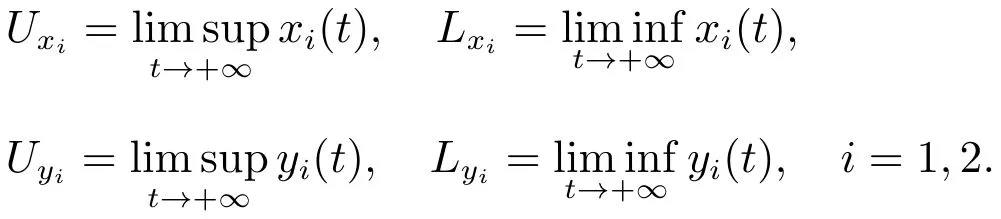
下面我们将用迭代法和比较定理证明

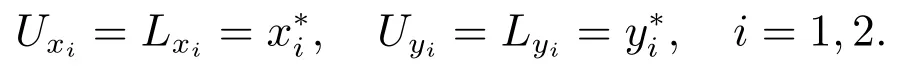
由系统(3)的第二个方程可得

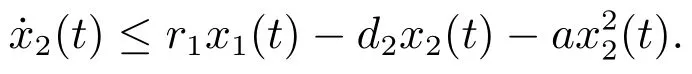
考虑辅助系统

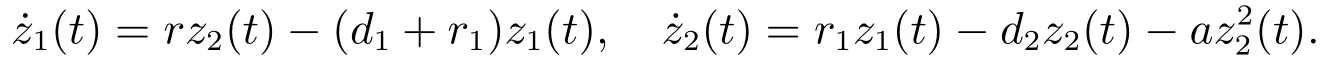
由文献[8]的引理2.2可知，当时

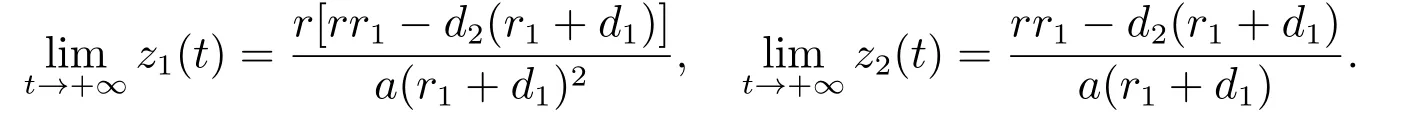
由比较定理可以得到

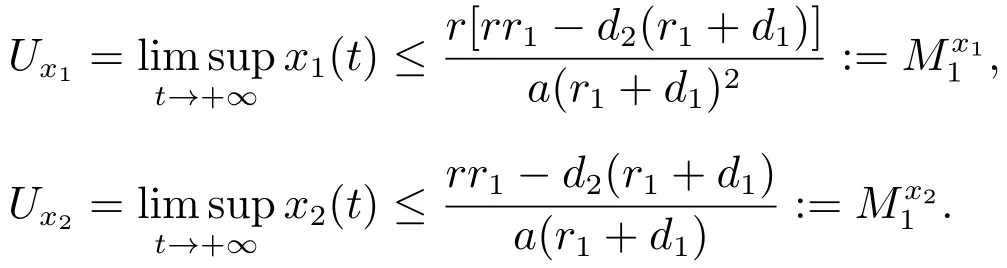
因此，对充分小的ε＞0，存在一个T1＞0，当t＞T1时，

对于t＞T1+τ，由系统(3)的第三个方程可得

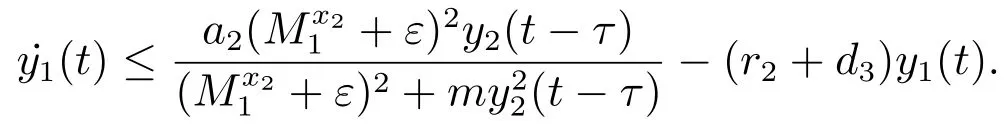
考虑辅助系统

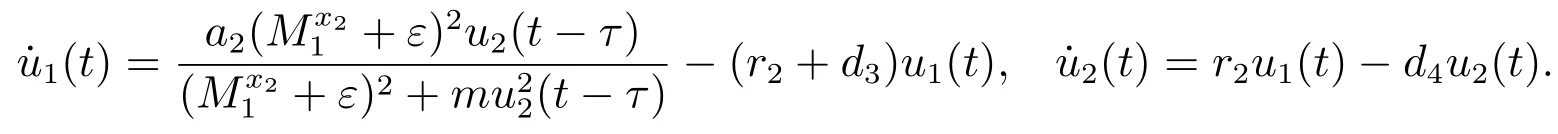
由文献[9]的引理2.4可知，当时

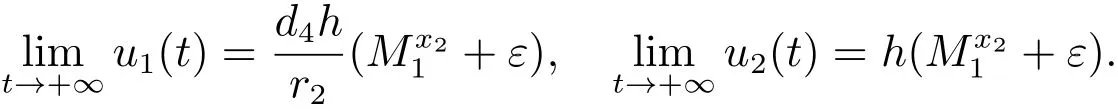
对充分小的ε＞0，由比较定理可以得到

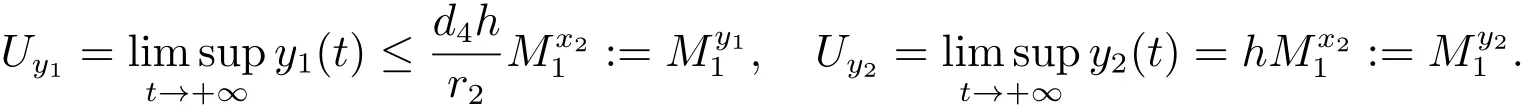
因此，对充分小的ε＞0，存在一个T2≥T1+τ，当t＞T2时，

对于t＞T2，由系统(3)的第二个方程可得

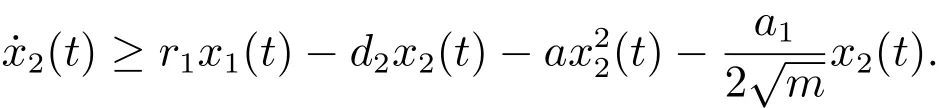
考虑辅助系统

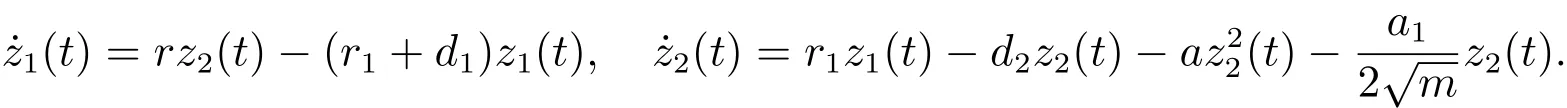
由文献[8]的引理2.2可知，当时

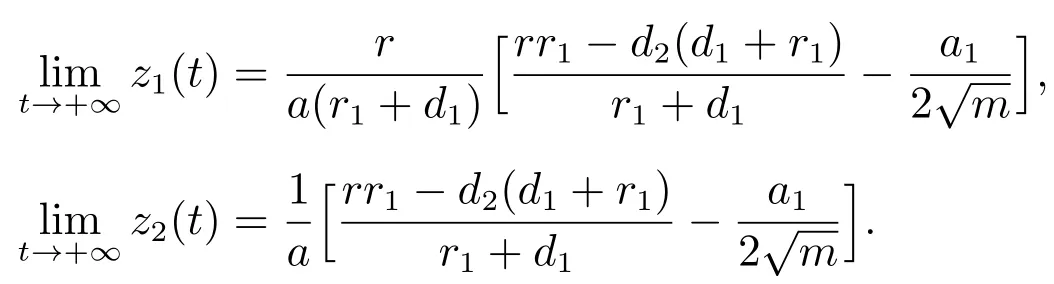
由比较定理可以得到

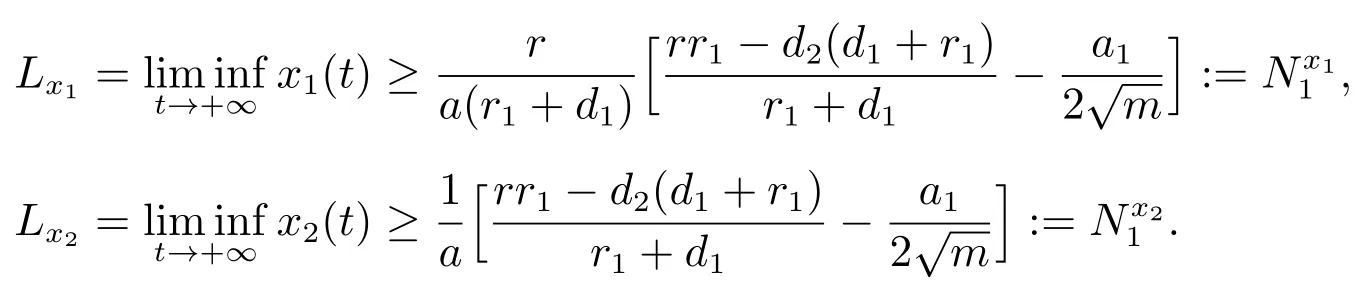
因此，对充分小的ε＞0，存在T3≥T2，当t＞T3时，

对于t＞T3+τ，由系统(3)的第三个方程可得

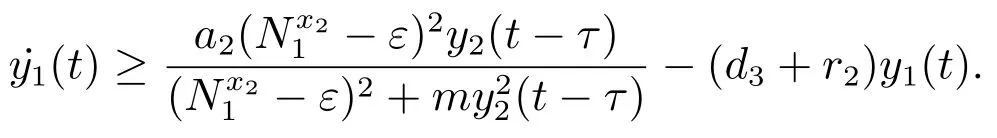
考虑辅助系统

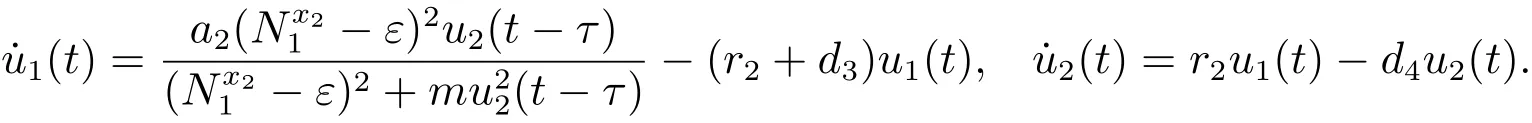
由文献[9]的引理2.4可知，当时，对充分小的ε＞0，由比较定理可以得到

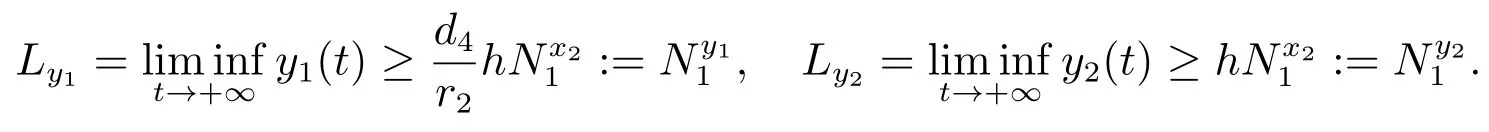
因此，对充分小的ε＞0，存在一个当t＞T4时，

对于t＞T4，由系统(3)的第二个方程可得

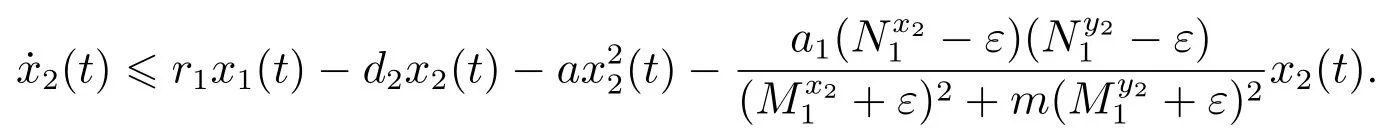
考虑辅助系统

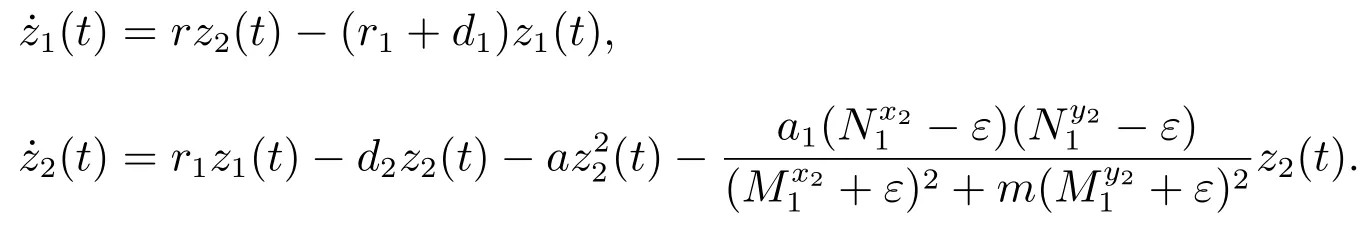
当(H3)成立时，由文献[8]的引理2.2，对充分小的ε＞0，由比较定理可以得到

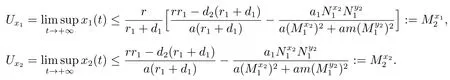
因此，对充分小的ε＞0，存在T5≥T4，使得当t＞T5时，

对于t＞T5+τ，由系统(3)的第三个方程可得

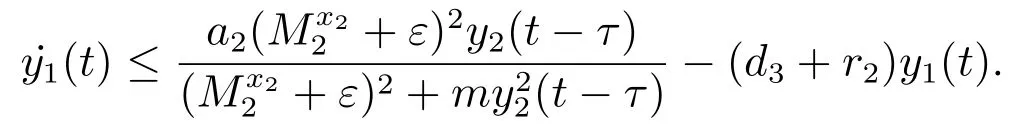
考虑辅助系统

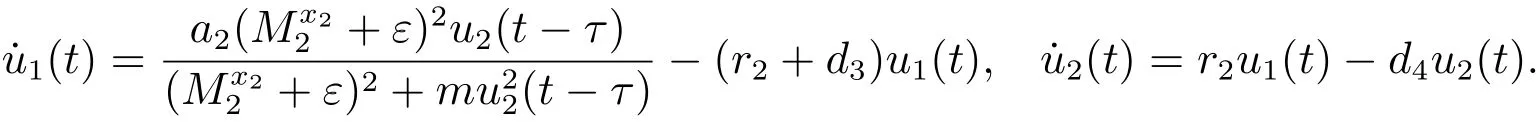
由文献[9]的引理2.4可知，当时，对充分小的ε＞0，由比较定理可以得到

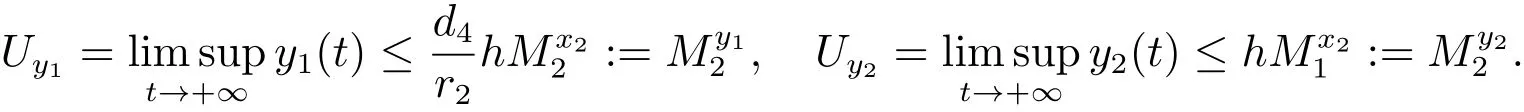
因此，对充分小的ε＞0，存在使得当t＞T6时，

对于t＞T6，由系统(3)的第二个方程可得

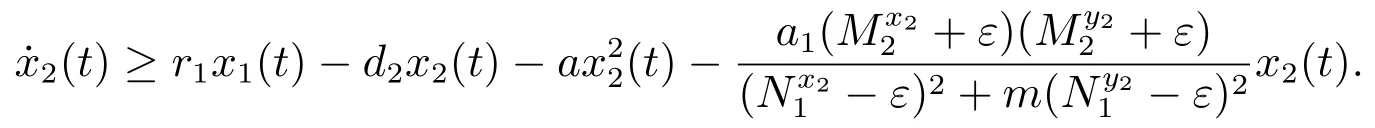
考虑辅助系统

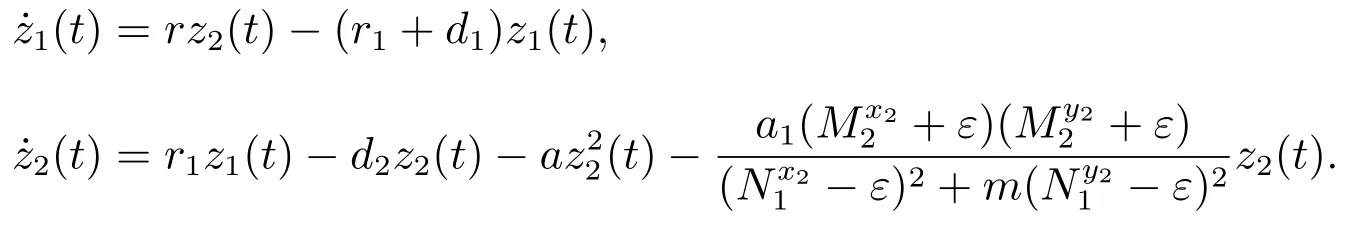
当(H3)成立时，由文献[8]的引理2.2，对充分小的ε＞0，由比较定理可以得到

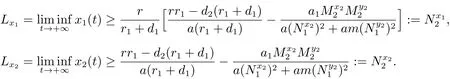
因此，对充分小的ε＞0，存在T7≥T6，使得当t＞T7时，

对于t＞T7+τ，由系统(3)的第三个方程可得

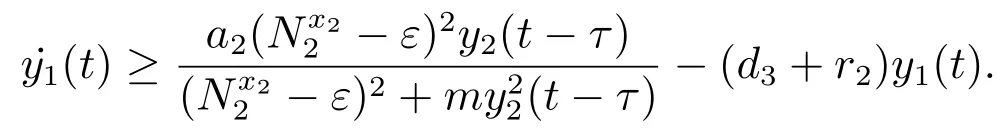
考虑辅助系统

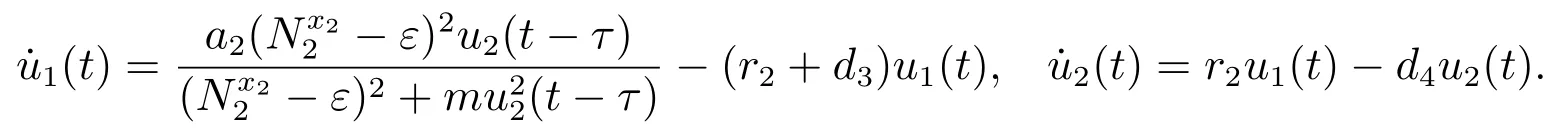
由文献[9]的引理2.4可知，当时，对充分小的ε＞0，由比较定理可以得到

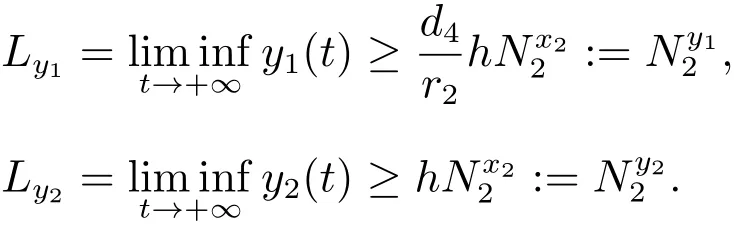
重复上述过程，我们可以得到八个序列对于n≥2，有下列关系式

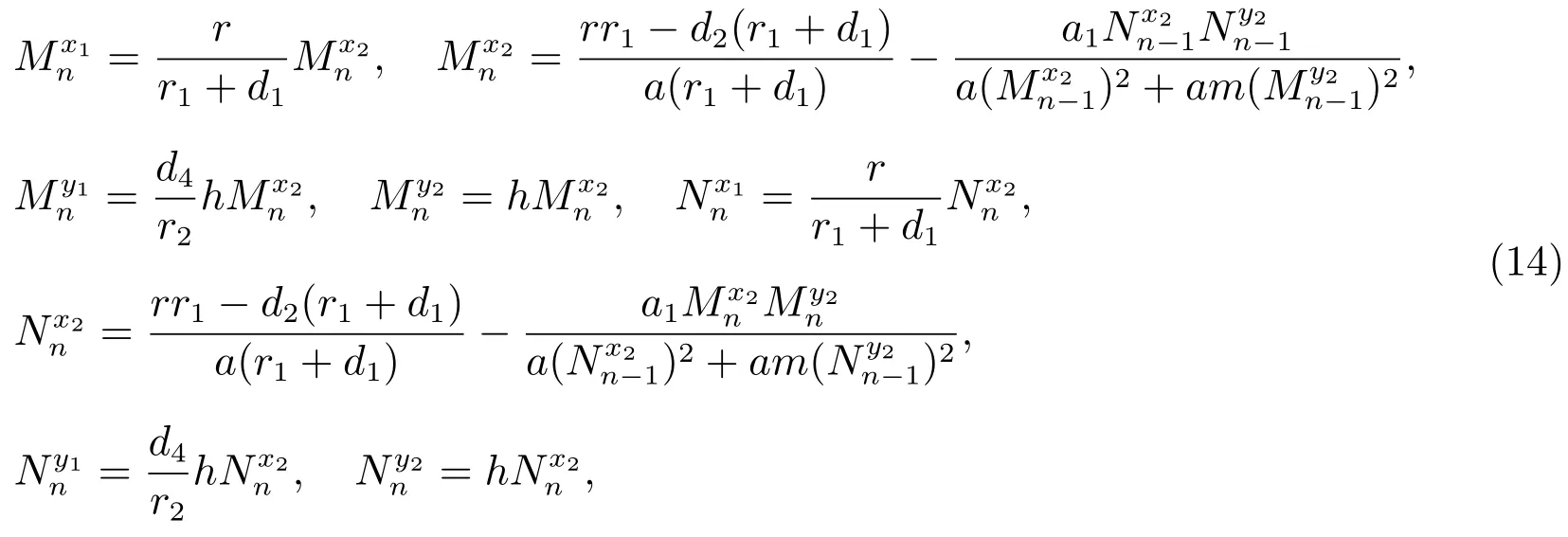
其中M和N满足下列关系式

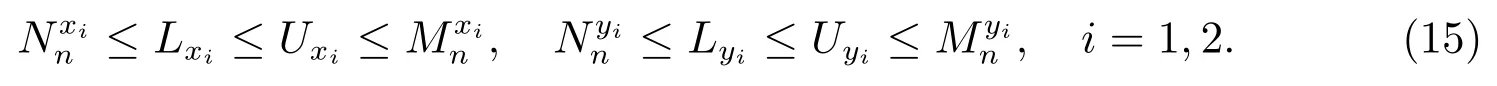
容易验证，序列和是单调递减的，和是单调递增的，因此序列和的极限存在，设

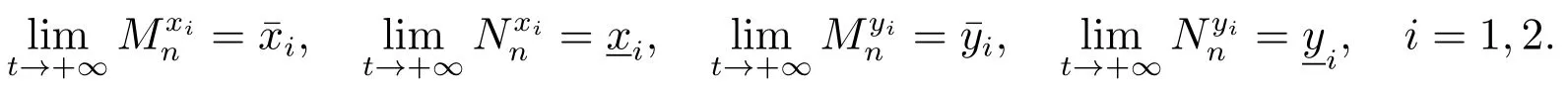
由(14)直接计算可以得到

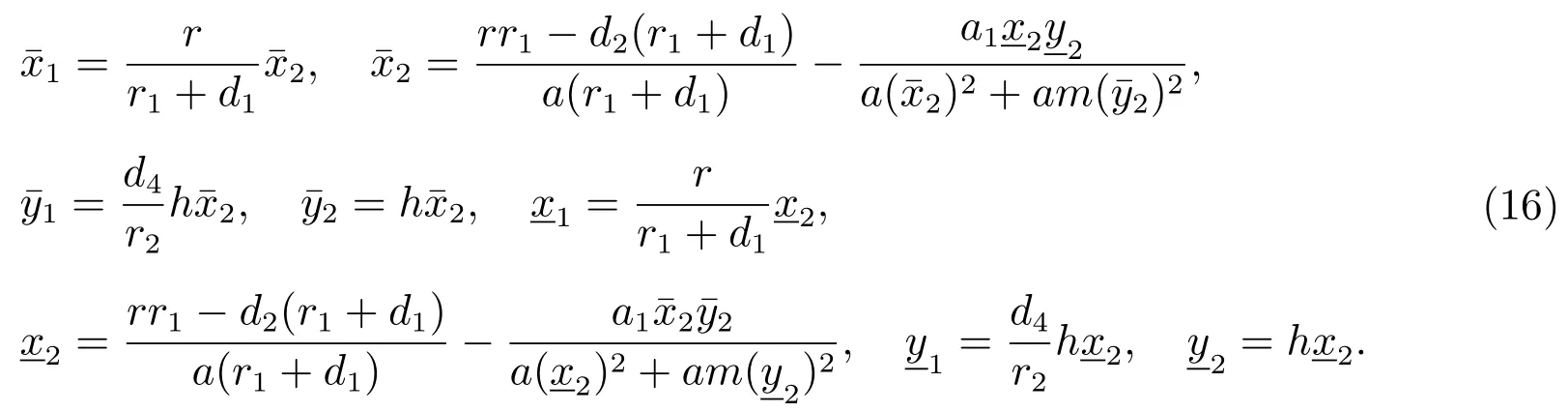
下面我们来证明由(16)计算可以得到

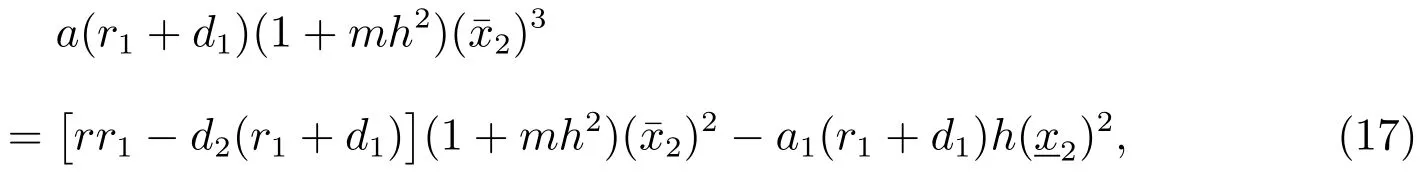
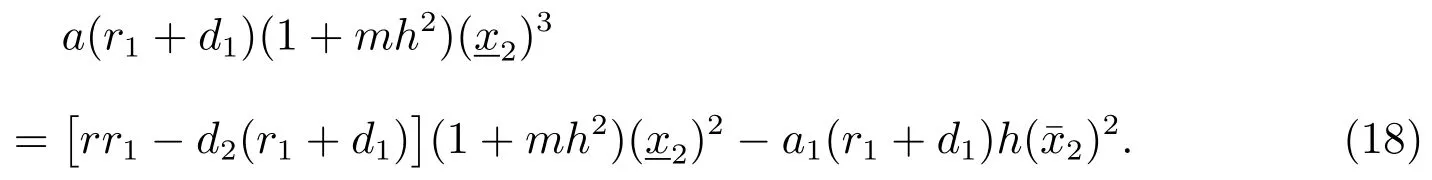
把(17)式减去(18)式可以得到

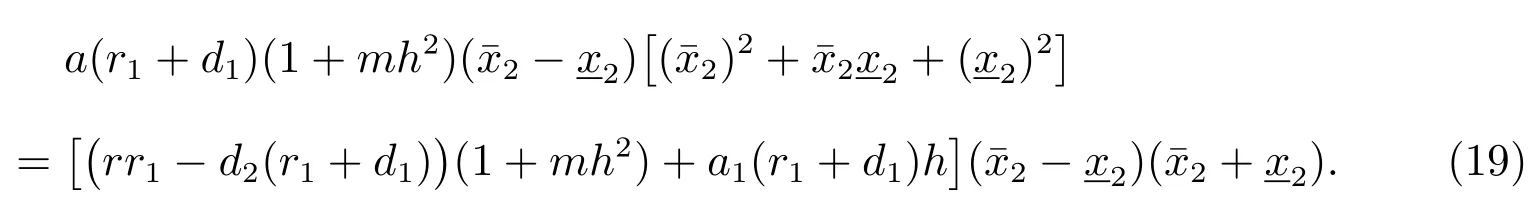
假设由(19)可以得到

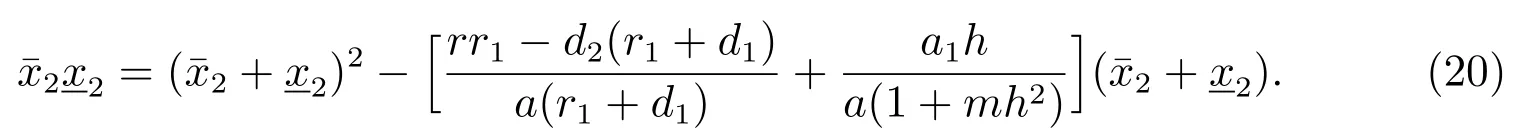
这样可以得到

注意到因此，当(H3)成立时，矛盾.因此由(16)可以得到和这样我们就证明了E∗是全局吸引的.

定理3.3设成立，对0若下列条件满足

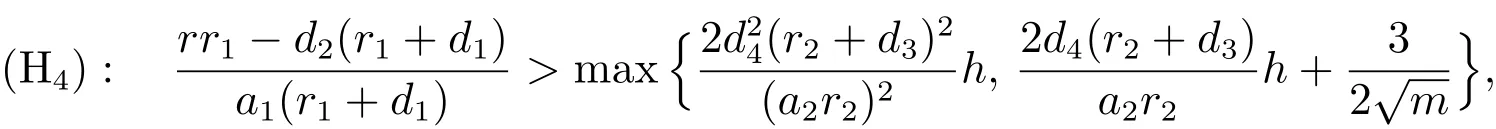
则系统(3)的正平衡点是全局渐近稳定的.

4 结论

本文中，我们讨论了一个比率依赖的捕食者种群和食饵种群均具有阶段结构的捕食模型的稳定性.通过分析特征方程，由Hurwitz判定定理分别讨论了该模型的边界平衡点和正平衡点的局部稳定性，得到了Hopf分支存在的充分条件；运用迭代法，由比较定理得到了该模型的边界平衡点和正平衡点全局稳定的充分条件.由定理3.1至定理3.3可以看出，当时，捕食者种群将灭绝；当和(H4)成立时，模型(3)将会持续生存.

参考文献：

[1]Arditi R,Perrin N,Saiah H.Functional response and heterogeneities:an experiment test with cladocerans[J].Oikos,1991,60(1):69-75

[2]Arditi R,Saiah H.Empirical evidence of the role of heterogeneity in ratio-dependent consumption[J].Ecology,1992,73(5):1544-1551

[3]Kuang Y,Beretta E.Global qualitative analysis of a ratio-dependent predator-prey system[J].Journal of Mathematical Biology,1998,36(4):389-406

[4]Xu R,Gan Q T,Ma Z E.Stability and bifurcation analysis on a ratio-dependent predator-prey model with time delay[J].Journal of Computational and Applied Mathematics,2009,230(1):187-203

[5]Kuang Y,So J W H.Analysis of a delayed two-stage population model with space-limited recruitment[J].SIAM Journal on Applied Mathematics,1995,55(6):1675-1695

[6]Wang W D,Chen L S.A predator-prey system with stage-structure for predator[J].Computers and Mathematics with Applications,1997,33(8):83-91

[7]Kuang Y.Delay Differential Equations with Applications to Population Dynamics[M].San Diego:Academic Press,1993

[8]Xu R,Ma Z E.The effect of stage-structure on the permanence of a predator-prey system with time delay[J].Applied Mathematics and Computation,2007,189(2):1164-1177

[9]Xu R,Ma Z E.Stability and Hopf bifurcation in a ratio-dependent predator-prey system with stage structure[J].Chaos Solitons and Fractals,2008,38(3):669-684

[10]Hale J.Theory of Functional Differential Equations[M].New York:Springer Heidelberg,1977

[11]Kuang Y.Delay Differential Equation with Application in Population Synamics[M].New York:Academic Press,1993