非奇异H-矩阵的一组判定条件∗

崔静静,陆 全,徐 仲,安晓虹

(西北工业大学应用数学系，西安 710072)

1 引言

在实际应用中如何有效地判定一个矩阵是否为非奇异H-矩阵，一直是人们关注的问题.近年来国内外众多学者对非奇异H-矩阵进行了深入的研究[1-11].本文利用矩阵指标集的k-级划分给出了非奇异H-矩阵一组判定条件，该判定条件推广和改进了已有的相关结果，丰富和完善了非奇异H-矩阵的判定方法.

用Cn×n表示n×n阶复矩阵的集合.设矩阵的指标集的k-级划分为

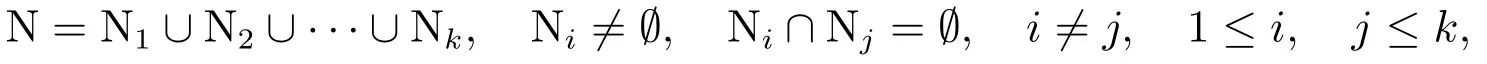
记

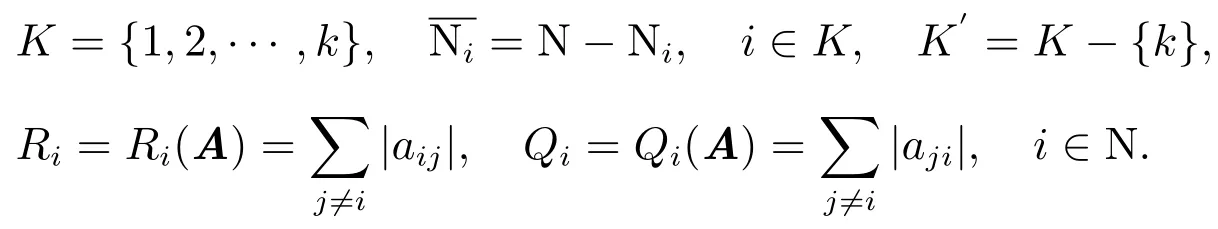
在本文总假设

定义1设如果则称A为严格对角占优矩阵，为A∈D；若存在正对角矩阵X，使得AX∈D，则称A为广义严格对角占优矩阵(即A为非奇异H-矩阵)，记

定义2设若存在使得

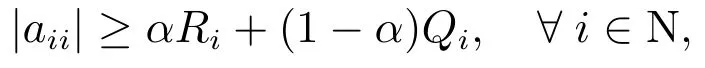
则称A为α-对角占优矩阵，记为若式中的不等式均严格成立，则称A为严格α-对角占优矩阵，记为若存在正对角矩阵X，使得则称A为广义严格α-对角占优矩阵，记为若式中至少有一个严格不等式成立且A不可约，则称A为不可约α-对角占优矩阵，记为；若对式中每个等式成立的下标i，都存在非零元素链满足则称A为具非零元素链α-对角占优矩阵，记为

引理1[1]设若满足下列条件之一，则

1)2)3)

引理2[2]设若存在正对角矩阵X，使得则

2 非奇异H-矩阵的一组判定条件

利用α-对角占优矩阵的性质，并利用划分矩阵指标集的方法，给出了如下的判定非奇异H-矩阵的新充分条件.

记

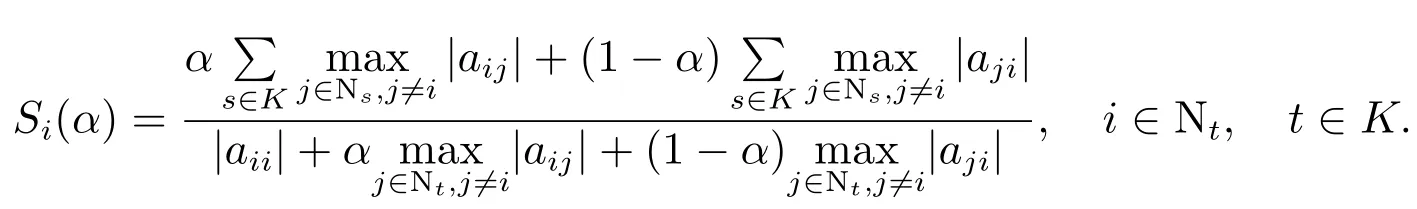
定理1设存在使得对任意的，有

令Wα为所有满足以上严格不等式的Nt之并集，若下列条件之一成立，则

1)Wα=N；2)A为不可约矩阵，且

3)对任意的存在非零元素链，使得

证明 由Ri/=0知，N.对，由Wα定义知

从而存在正数ε，使得

取正对角矩阵令其中

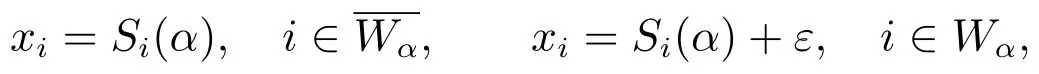
不失一般性，设

1)对任意的由(1)、(2)及

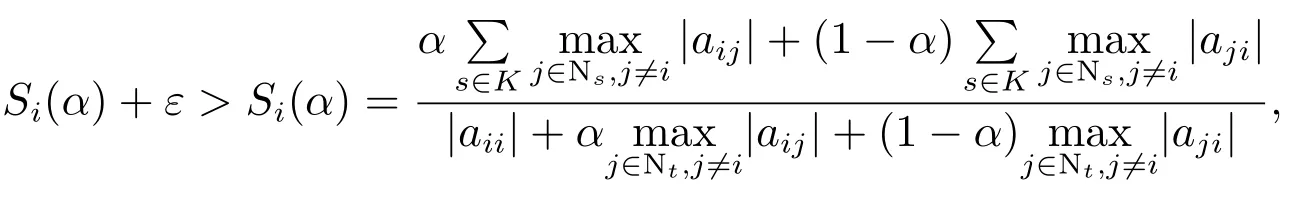
得

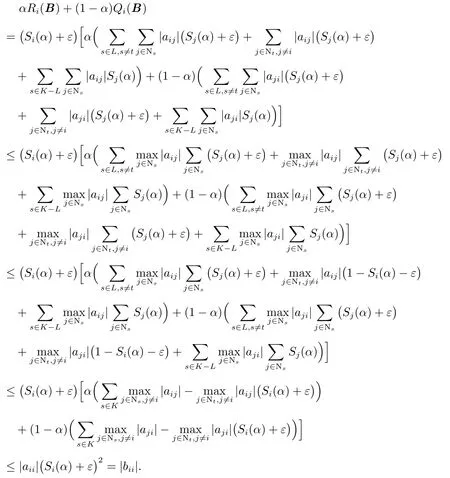
2)对任意的有

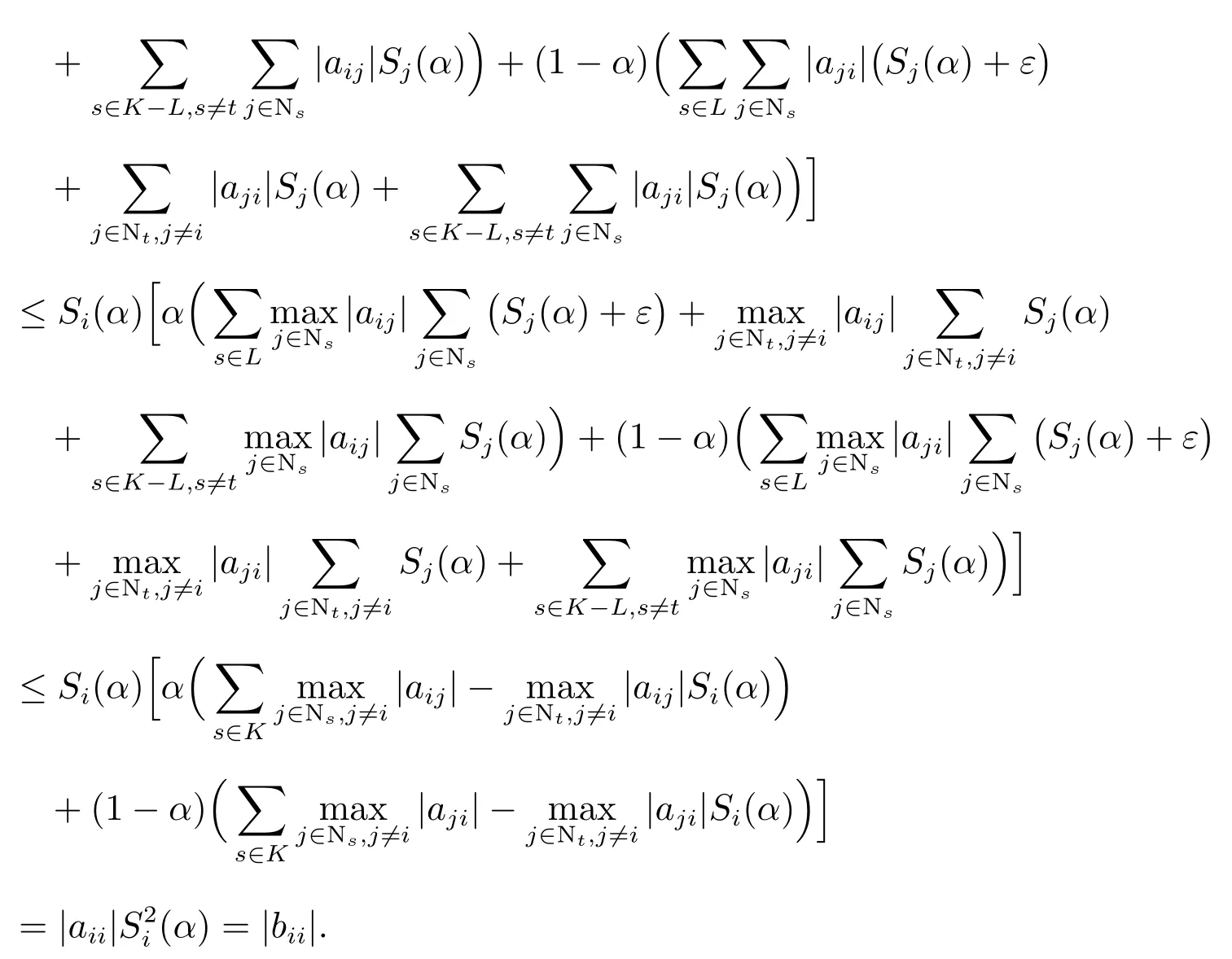
综上所知：且：

1)若Wα=N，则

2)因B不改变A的不可约性，且故由定义2知

3)因B不改变A的非零元素链，故由定义2知

于是，由引理1知再由引理2知

注1文献[4]中定理2.1(III)是本文定理1当k=1时特例；文献[7]中定理2为本文定理1当k=2,α=1时特例；文献[9]中定理1为本文定理1当α=1时特例.

记

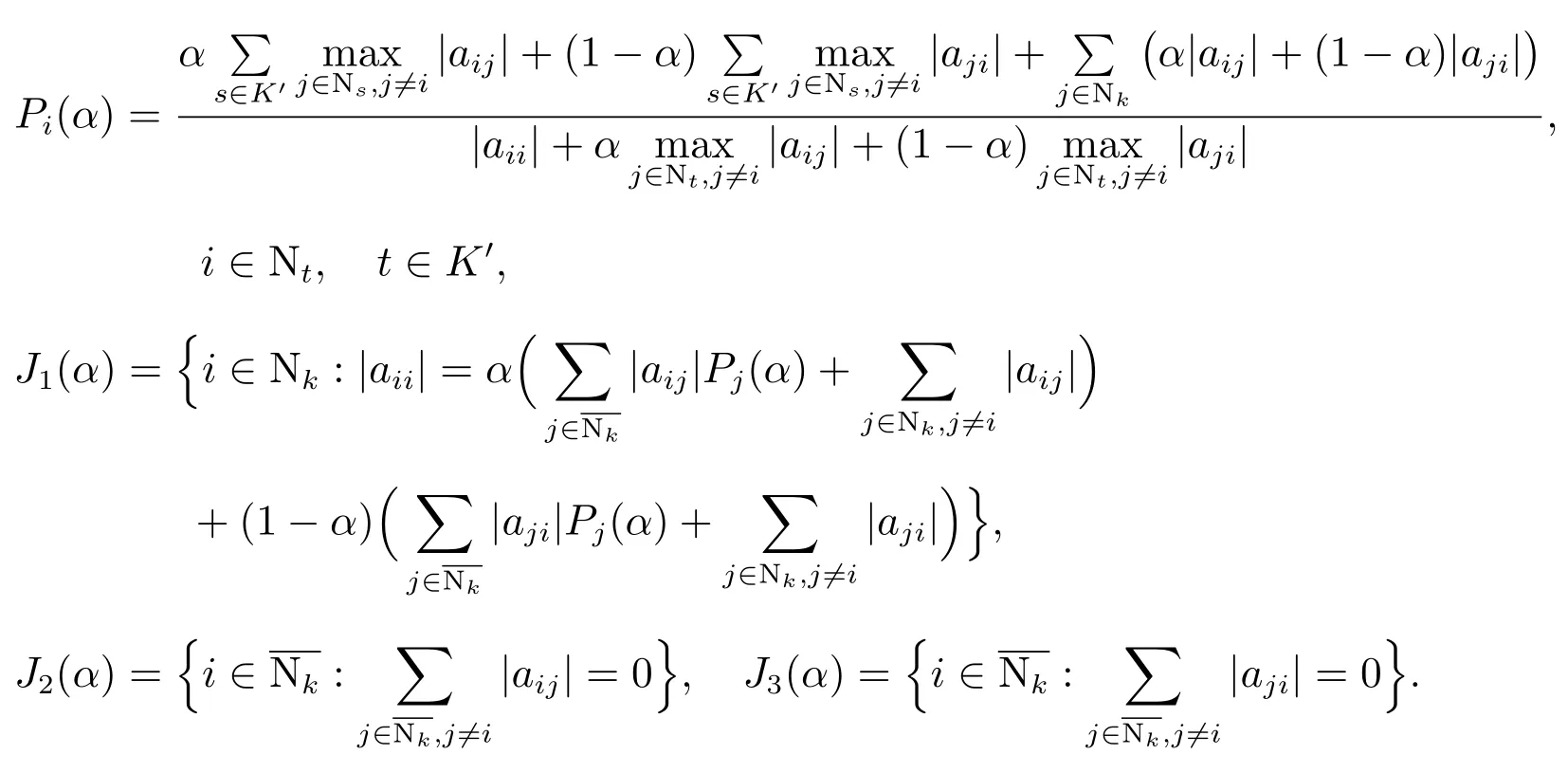
定理2设存在使得对任意的有

且

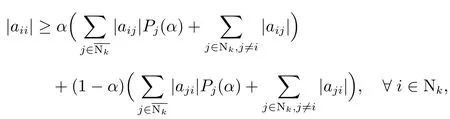
若A还满足下列条件之一，则

1)

2)A为不可约矩阵，且

3)对任意的存在非零元素链使得

图1中阴影部分为空白部分为

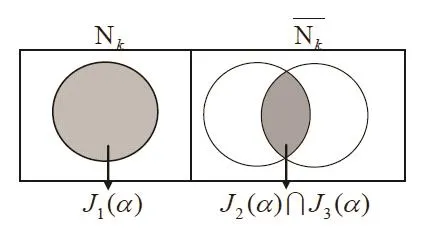
图1:J1(α),J2,(α),J3(α)之间关系图

证明 由Ri/=0知且由式(3)，有

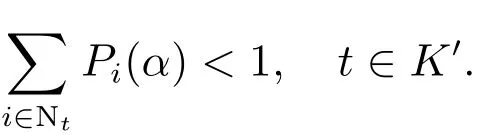
令

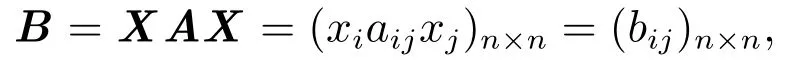
其中

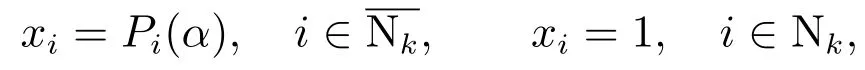
下证

(a)对任意的

首先，考虑情形.

当时，有

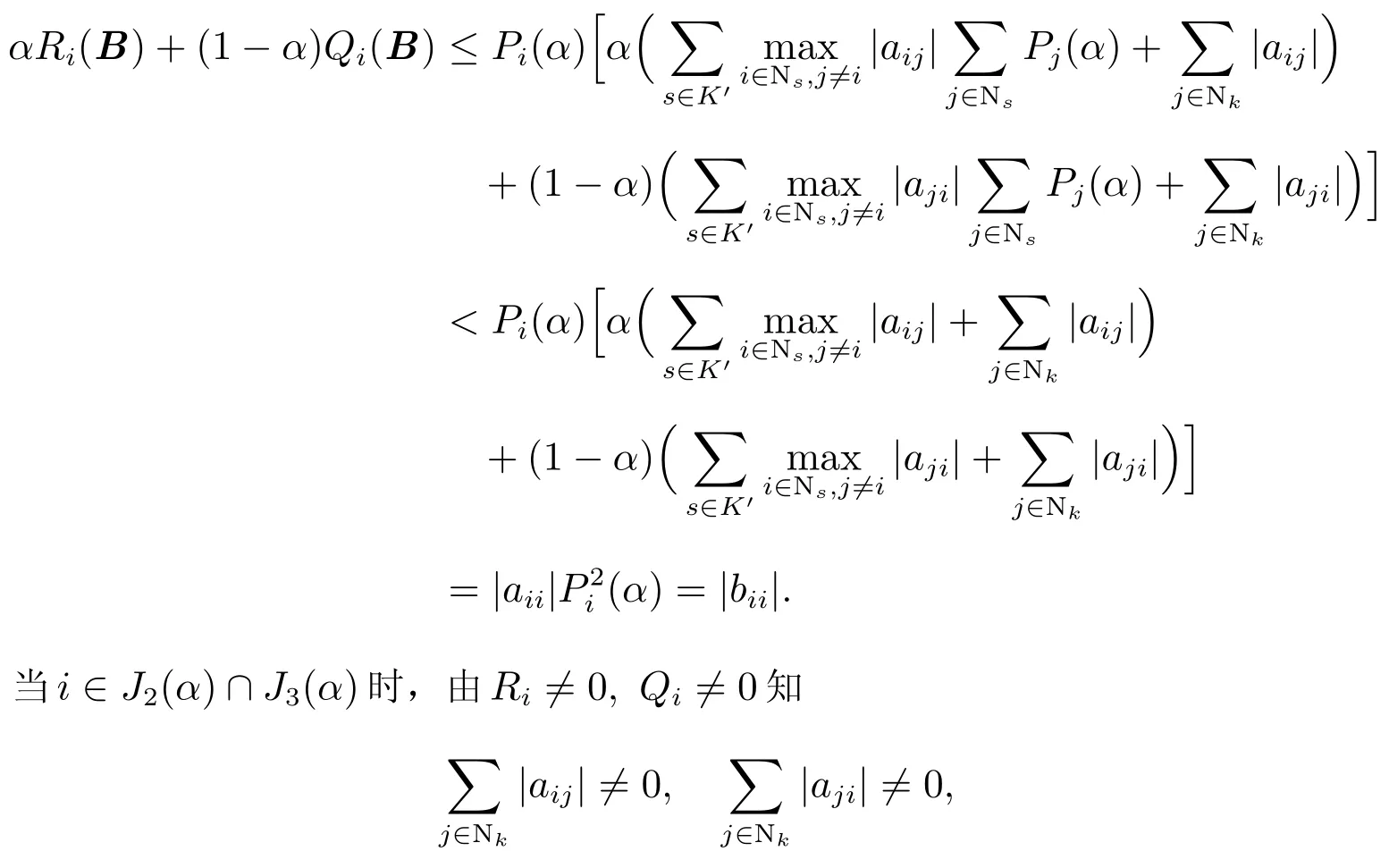
从而

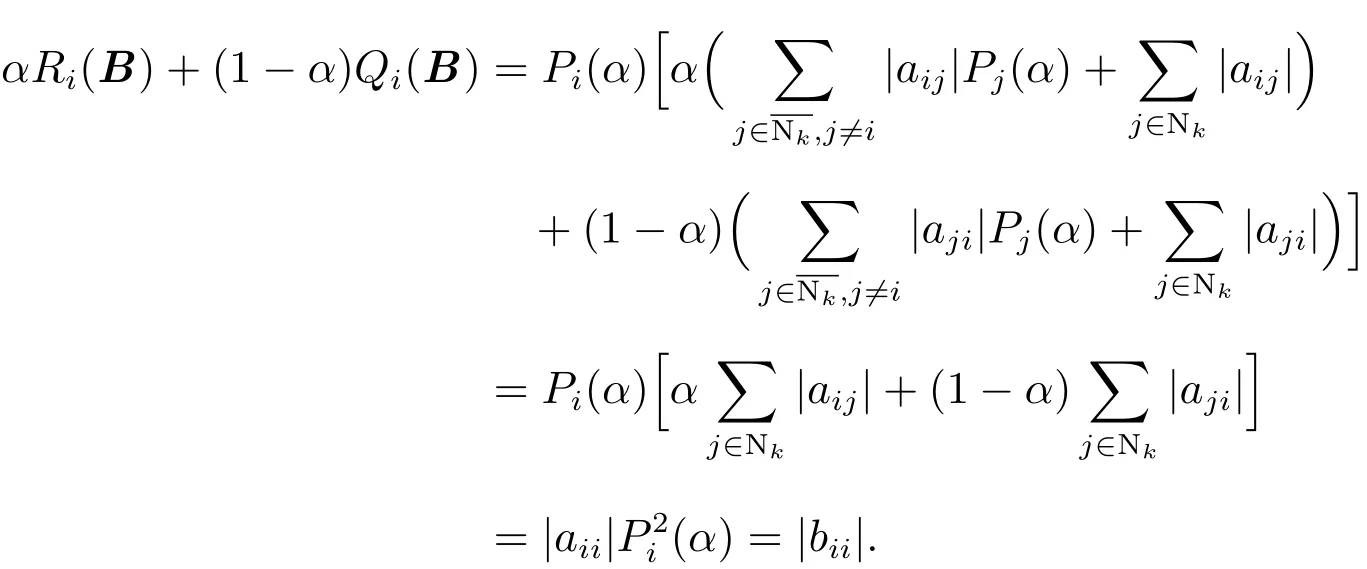
其次，考虑与至少有一个不为零的情形.

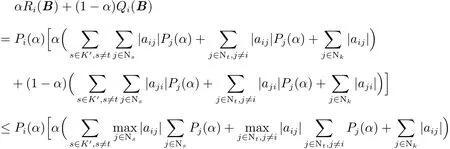
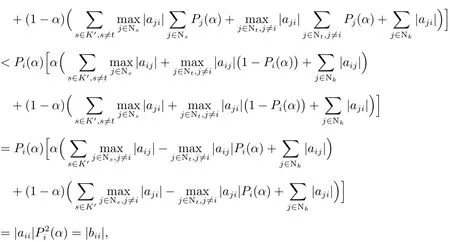
故对任意的

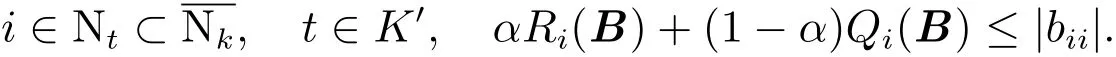
(b)对任意的当时，有

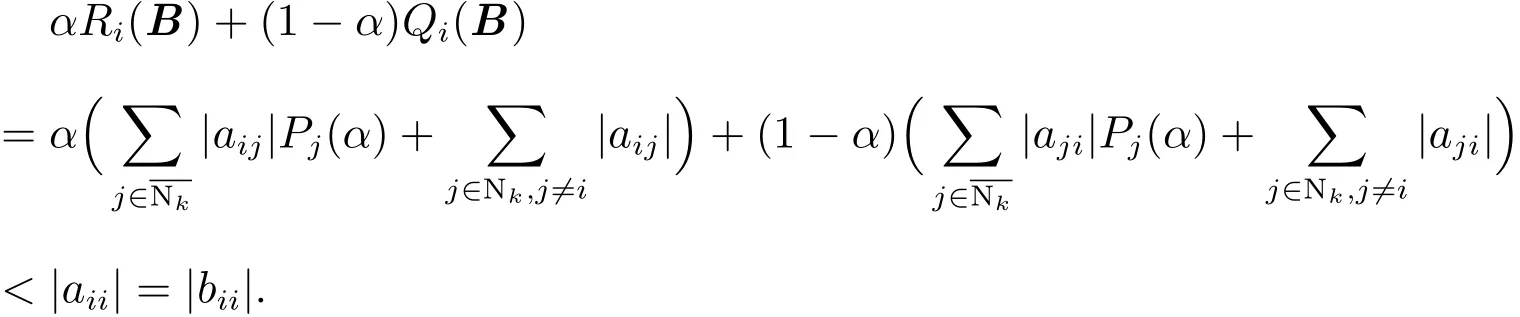
当时，有

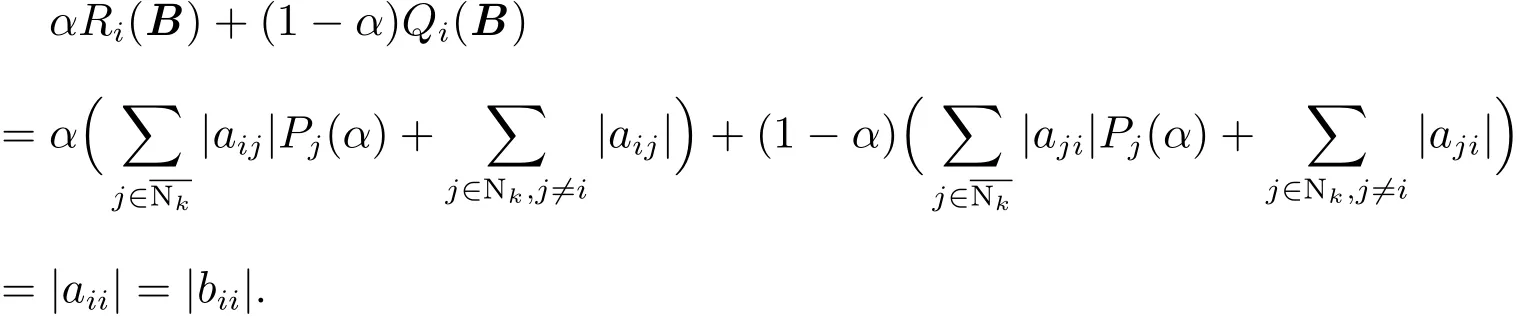
综上所述：且：

1)由(b)可知，当J1(α)=Ø时，有

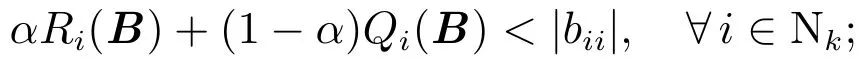
由(a)可知，当时，有

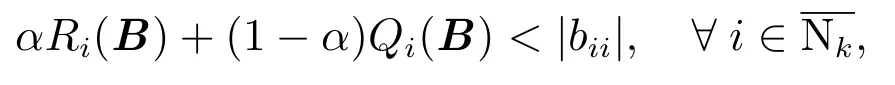
故当时，

2)当时，有

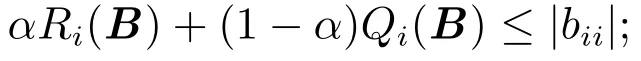
由于

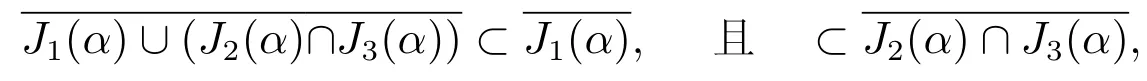
故由(a)及(b)可知，当时

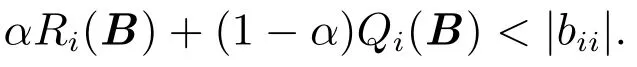
又因B不改变A的不可约性，故若则

3)由于对任意的存在非零元素链使得故B具非零元素链，则

于是由引理1知再由引理2知

注2文献[4]中定理2.2(II)是本文定理2当k=2时特例；文献[9]中定理2为本文定理2当α=1时特例；文献[10]中定理1为本文定理2当都是单点集，并且都是A的对角占优行，而Nk是A的非对角占优行集时特例.

3 数值算例

例1 设矩阵

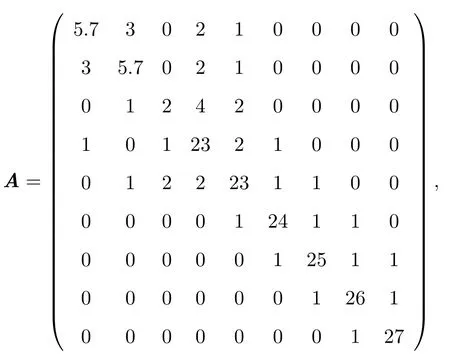
则用文献[3]中定理1(3°)，文献[4]中定理2.1(III)，文献[10]中定理1及文献[11]中定理1均不能判定A是否为非奇异H-矩阵，而用本文定理1可判定A为非奇异H-矩阵.事实上，对文献[3]中定理1，有

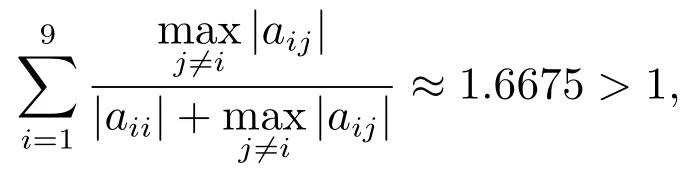
文献[4]中定理2.1，有

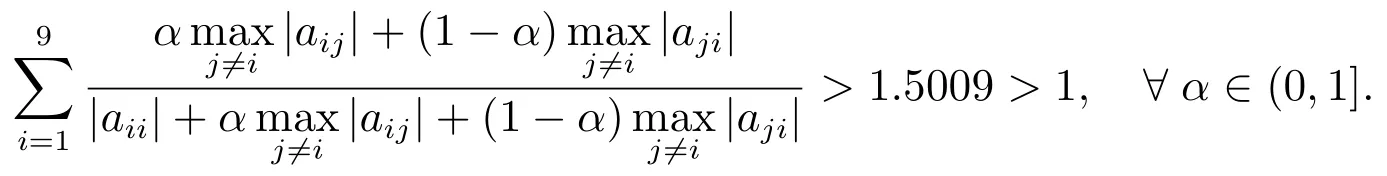
对文献[10]中定理1，有且

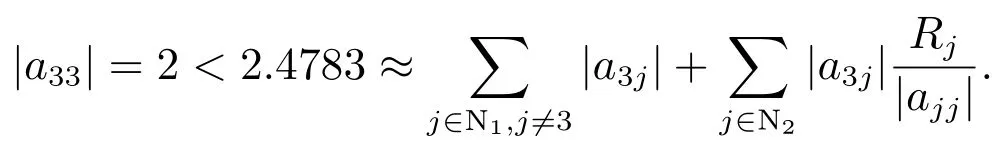
对文献[11]中定理1，有且

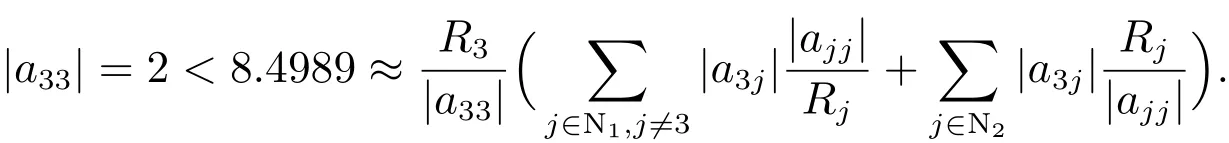
而对本文定理1，取α=0.1,k=3，即

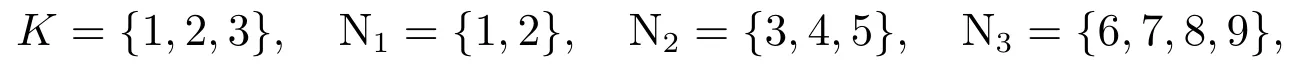
则

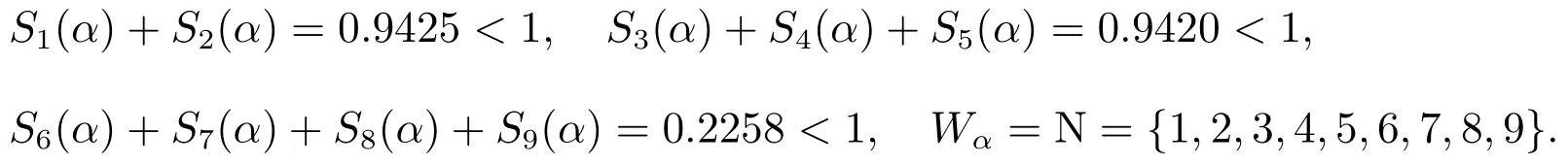
满足本文定理1条件(1)，故用本文定理1可判定A为非奇异H-矩阵.事实上，取正对角矩阵D=diag(1,1,5,0.5,1,1,1,0.5,1)时，有

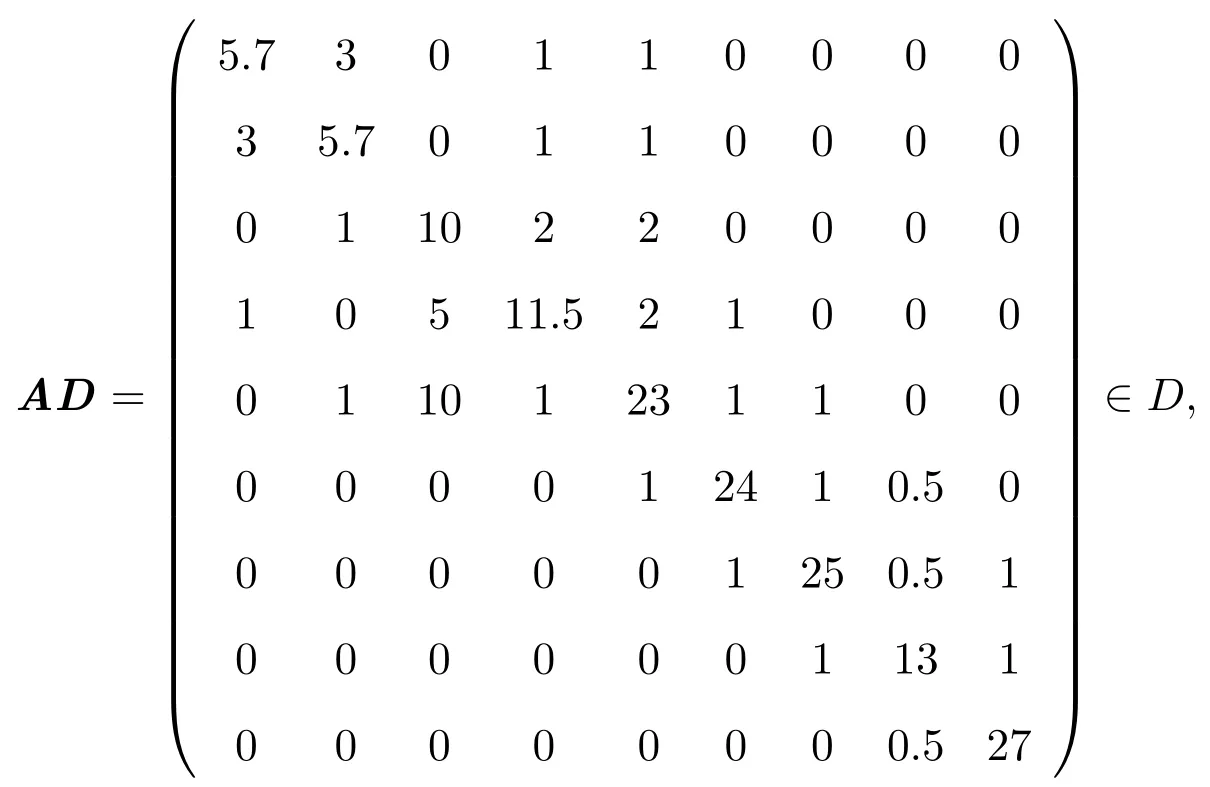
即A确为非奇异H-矩阵.

例2设矩阵

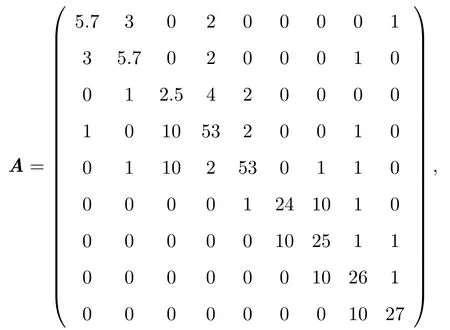
则用文献[3]中定理2(2°)，文献[4]中定理2.2(II)，文献[10]中定理1及文献[11]中定理1均不能判定A是否为非奇异H-矩阵，而用本文定理2可判定A为非奇异H-矩阵.事实上，在文献[3]中，有且

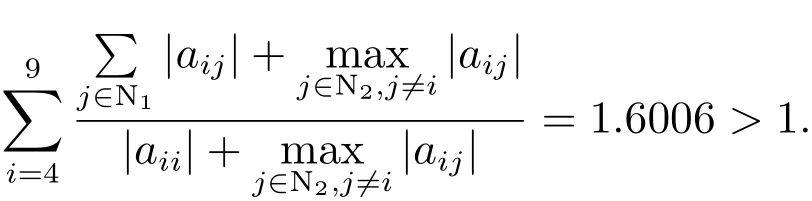
在文献[4]中，对任意的均有且令则对任意的有

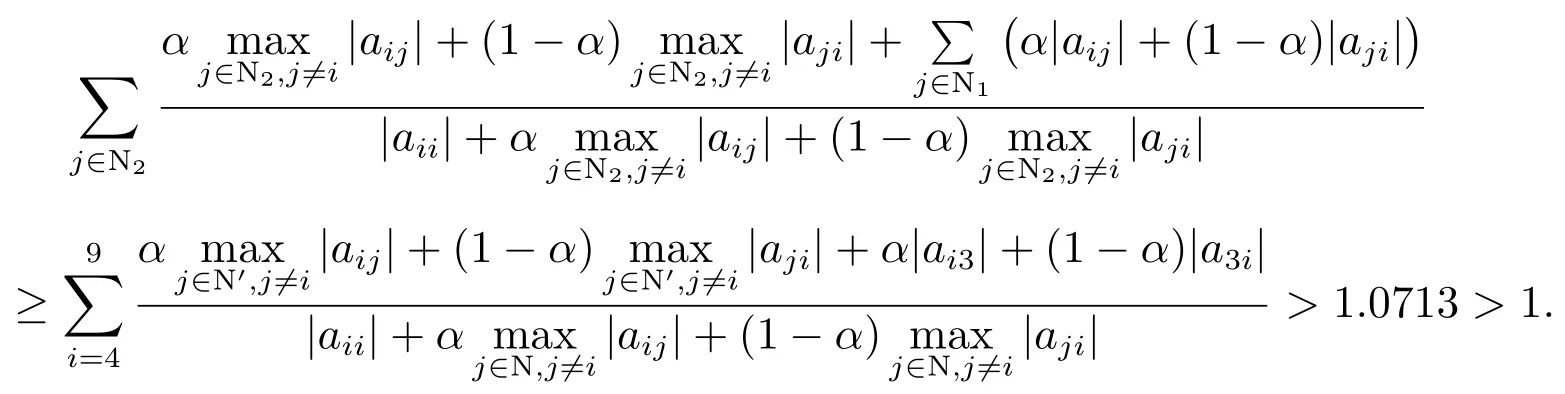
在文献[10]中，有且

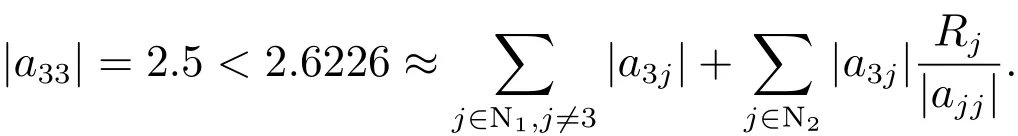
在文献[11]中，有且

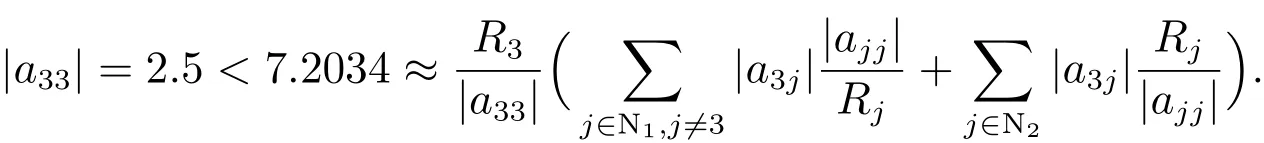
而对本文定理2，取α=0.1,k=3，即

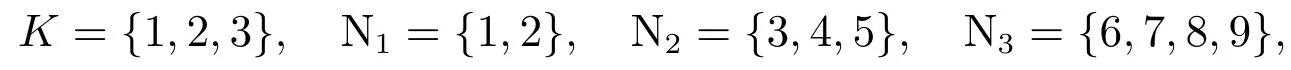
则

且

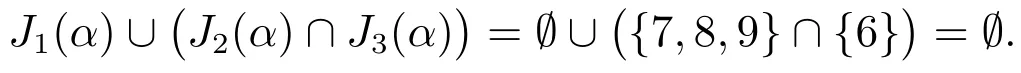
满足本文定理2条件(1)，故用本文定理2可判定A为非奇异H-矩阵.事实上，取正对角矩阵D=diag(1,1,2,0.5,0.5,1,1,0.5,1)时，有

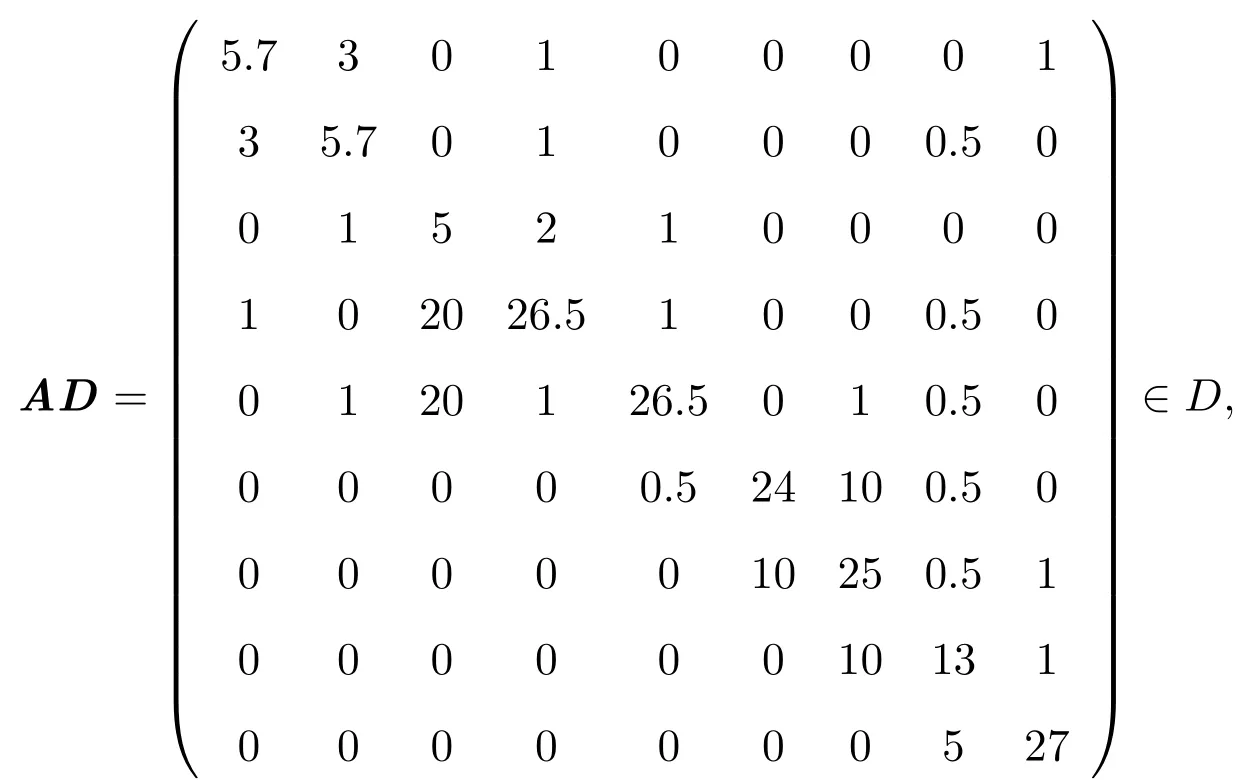
即A确为非奇异H-矩阵.

参考文献：

[1]Sun Y X.An Improvement on a theorem by ostrowski and its applications[J].Northeastern Mathematical Journal,1991,7(4):497-502

[2]Liu J Z,Zhang C Q.Some criteria for nonsingularH-matrices[J].Natural Science Journal of Xiangtan University,2008,30(3):21-29

[3]徐仲，陆全.判定广义严格对角占优矩阵的一组充分条件[J].工程数学学报，2001,18(3):11-15 Xu Z,Lu Q.A set of sufficient condition for identifying generalized strictly diagonally dominant matrices[J].Chinese Journal of Engineering Mathematics,2001,18(3):11-15

[4]匡巧英.H-矩阵和广义H-矩阵的一些判别方法[D].湘潭：湘潭大学，2013 Kuang Q Y.Some determinate conditions for nonsingularH-matrices and generalizedH-matrices[D].Xiangtan:Xiangtan University,2013

[5]孙玉祥.广义对角占优矩阵的充分条件[J].高等学校计算数学学报，1997,19(3):216-233 Sun Y X.Sufficient condition for generalized dominant matrices[J].Numerical Mathematics a Journal of Chinese Universities,1997,19(3):216-233

[6]王磊磊，席博彦，刘建州.非奇异H-矩阵的几个充分条件[J].高校应用数学学报，2014,29(1):55-62 Wang L L,Xi B Y,Liu J Z.Several sufficient conditions for judging nonsingularH-matrices[J].Applied Mathematics a Journal of Chinese Universities,2014,29(1):55-62

[7]侯进军，李斌.H-矩阵的一组新判定[J].应用数学学报，2008,31(2):266-270 Hou J J,Li B.Some new condition for nonsingularH-matrices[J].Acta Mathematicae Applicatae Sinica,2008,31(2):266-270

[8]谢清明.判定广义对角占优矩阵的几个充分条件[J].工程数学学报，2006,23(4):757-760 Xie Q M.Sufficient condition for generalized diagonally dominant matrices[J].Chinese Journal of Engineering Mathematics,2006,23(4):757-760

[9]冷春勇.非奇异H-矩阵的判定[J].应用数学学报，2011,34(1):50-56 Leng C Y.Criteria for nonsingularH-matrices[J].Acta Mathematicae Applicatae Sinica,2011,34(1):50-56

[10]黄廷祝.非奇H-矩阵的简捷判据[J].计算数学，1993,15(3):318-328 Huang T Z.Some simple determinate conditions for nonsingularH-matrices[J].Mathematical Numerica Sinica,1993,15(3):318-328

[11]Gan T B,Huang T Z.Simple criteria for nonsingularH-matrices[J].Linear Algebra and its Applications,2003,374:317-326