众多临近空间飞行器的最优轨迹规划

马晓华, 南英, 惠耀洛, 万正富, 周生龙

(1.南京航空航天大学 航天学院, 江苏 南京 210016;2.火箭军驻307厂军事代表室, 江苏 南京 210006)



众多临近空间飞行器的最优轨迹规划

马晓华1,2, 南英1, 惠耀洛1, 万正富2, 周生龙2

(1.南京航空航天大学 航天学院, 江苏 南京 210016;2.火箭军驻307厂军事代表室, 江苏 南京 210006)

摘要:针对众多临近空间飞行器在复杂飞行环境的最优轨迹规划问题,采用改进的动态规划法和基于共轭梯度法的多点边值组合算法求解了多目标优化问题,得到了全部飞行器的最优飞行轨迹。仿真结果表明,该算法能够在考虑多种环境条件约束和飞行器自身条件约束的情况下,快速规划出众多飞行器的最优飞行轨迹,具有一定的学术价值和工程应用价值。

关键词:众多临近空间飞行器; 飞行威胁区; 飞行任务点; 最优飞行轨迹

0引言

近年来,国内外学者在复杂飞行环境中飞行器轨迹优化问题的研究方面取得了重要进展。考虑的典型飞行环境主要有两大类:一是要求飞行器路过给定的任务点[1-4];二是要求飞行器躲避(或绕开)威胁区(或飞行禁区)[5-7]。在同时存在飞行威胁区和飞行任务点约束的轨迹优化问题方面,文献[8]采用伪谱法和非线性动态规划法,以飞行时间最短为性能指标,得到了单架高超声速巡航飞行器的最优飞行轨迹。文献[9]采用基于支持向量机与遗传算法的组合优化算法，提高了临近空间飞行器轨迹优化的效率。

本文综合考虑存在飞行任务点和飞行威胁区等约束条件,采用改进的动态规划法和共轭梯度法的组合算法,对众多临近空间飞行器在复杂飞行环境中的轨迹进行全局一体化优化。

1问题的提出与表述

众多临近空间飞行器在复杂飞行环境中的最优轨迹规划,要求全部飞行器从各自起始点飞行至最终目标点的过程中,使飞行器编队整体飞行总时间最小,同时受到威胁区的危险度最小，并且最准确地飞行路过目标点,完成对地面预定目标的攻击。

飞行器的复杂飞行环境包括:飞行威胁区、飞行任务点以及全部临近空间飞行器在飞行过程中相互之间需要保持一定的安全距离。主要考虑的性能指标和约束条件有:

(1)使全部飞行器避开飞行威胁区,选用性能指标:

(1)

(2)

其中:

式中:n为飞行器编号,n=1,2,…,nmax;i为飞行威胁区编号,i=1,2,…,imax;rni为第n架飞行器与第i个飞行威胁区的安全距离;dimin为各飞行器与第i个飞行威胁区边界之间必须满足的最小安全距离。

(2)使飞行器编队路过全部飞行任务点,要求飞行器编队尽量准确地通过设定的任务点,每架飞行器路过每个任务点最多一次,且至少路过一个任务点,每个任务点至少被一架飞行器路过。取性能指标:

(3)

(4)

(5)

式中:pnj=0则第n架飞行器不路过第j个任务点,pnj=1则第n架飞行器路过第j个任务点;tnj为第n架飞行器到达第j个任务点所需时间,由于每架飞行器速度差别不大,实际计算过程中可用第n架飞行器到第j个任务点的距离rnj代替。

以上是假设共有nmax架临近空间飞行器,imax个飞行威胁区,jmax个飞行任务点;(xi,yi,zi)为第i个飞行威胁区的边界坐标,(xj,yj,zj)为第j个飞行任务点的坐标,(xn,yn,zn)为第n架飞行器的位置坐标。

(3)为使临近空间飞行器编队最快到达地面指定目标进行攻击任务,以飞行器编队攻击地面固定目标的总体飞行时间最短的性能指标为:

(6)

(4)全部临近空间飞行器在飞行过程中任意两架之间的空间距离:

(7)

其中:

式中:n1,n2=1,2,…,nmax,n1≠n2;dnmin为两架临近空间飞行器之间的最小安全距离。

综合考虑上述因素,得到众多临近空间飞行器在复杂飞行环境中的最优轨迹规划的性能指标为:

式中:p1,p2,p3为加权系数。

2轨迹优化数值算法

为采用直接法与间接法的组合优化算法,将约束条件分为可视性约束条件和非可视性约束条件两类:(1)可视性约束条件:在三维几何空间中具有明显边界条件的空间区域约束;(2)非可视性约束条件:在三维几何空间中没有明显边界条件的其他飞行条件约束。

临近空间飞行器的运动方程为:

(8)

式中:xn=[xn(t),yn(t),zn(t),vn(t),θn(t),ψvn(t)],其中的各元素依次为飞行器的三维位置坐标、飞行速度、轨迹倾角和偏航角;un为飞行器的控制量;ξn为包括随机风场在内的随机干扰。把全部飞行器的运动微分方程式(8)转化成非线性离散化的状态差分方程:

xn(k+1)=f ′(xn(k),un(k), ξn(k),k)

(9)

式中：n=1,2,…,nmax;k=0,1,…,N-1。

首先采用改进的动态规划法求解满足可视性约束条件的众多临近空间飞行器的近似最优轨迹。计算步骤由N+1步组成:

第1步:计算xn(0)～xn(1)的轨迹。

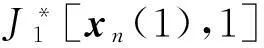
第2步:计算xn(1)～xn(2)的轨迹。

式中:un(1)∈Φn(1)，un(1)为第2步动态规划的决策变量,Φn(1)为第2步动态规划的允许决策集合。由xn(2)=f(xn(1),un(1),ξn(1),1)可以求得un(1)与J2*[xn(2),2]。

……

第N步:计算xn(N-1)～xn(N)的轨迹。

式中:un(N-1)∈Φn(N-1),un(N-1)为第N步动态规划的决策变量,Φn(N-1)为第N步动态规划的允许决策集合。

第N+1步:由上述N步求得的最优决策变量得到全部飞行器的最优控制决策变量和近似最优飞行轨迹。采用微分法获得全部飞行器的近似飞行速度和加速度,以及相应的控制变量序列。

然后在非可视性约束条件下,基于最优控制中的极值原理与共轭梯度法,采用多点边值算法,以动态规划法得到的控制变量序列作为初值,进行多目标轨迹优化而求得最优控制律。

关于多点边值问题的求解算法简述如下:

由动态规划法得到的全部N段飞行器近似最优轨迹xn(k)(k=0,1,2,…,N),从起点飞行状态xn(0)开始,以每一段飞行轨迹的末端为约束,每一段的起始点飞行状态xn(k)(k=1,2,…,N-1)均为上一段由两点边值问题求解获得的末端飞行状态点xn(k-1)(k=1),即:

其中,轨迹优化的性能指标为:

由此,逐段求解两点边值问题,便可得到满足全部各种约束条件的所有飞行器的四维飞行轨迹xn*(t)和飞行控制律un*(t)。

3数值仿真与分析

以7架临近空间飞行器协同攻击地面固定目标为例,整个巡航飞行过程中需避开9个飞行威胁区和路过4个飞行任务点。

全部飞行器的起点均为x轴的零点,释放高度为50 km,在z轴上一字排开，且在z轴上的位置坐标为(-400,-80,-20,90,220,290,310) km。发射时初始速度为1 800 m/s,初始轨迹倾角和偏航角均为0°。地面目标点位置坐标为(1 800 km,0,0)。其他仿真条件为:(dimin,dnmin,dfmax)=(1 000,100,10) m;vfmin=1 200 m/s,aymax=azmax=15g;(θfmin,θfmax,ψvfmin,ψvfmax)=(-90°,-50°,-10°,10°);rni>1 km时,(p1,p2,p3)=(0.3,0.2,0.5);rni≤1 km时,(p1,p2,p3)=(0.5,0.4,0.1)。

定义A1～A4为半球型飞行威胁区,A5～A9为柱形飞行威胁区,B1～B4为飞行任务点,其区域中心位置坐标和半径大小信息如表1和表2所示。数值仿真结果如图1～图3所示。

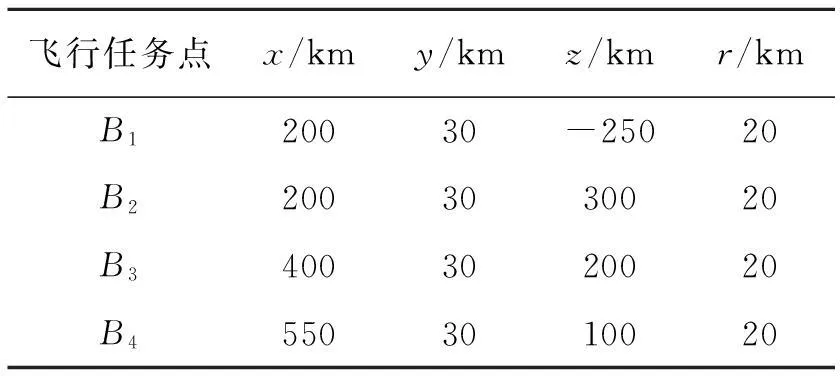
表2　飞行任务点的位置分布情况

图1　飞行器的三维飞行轨迹Fig.1　3D flight trajectories of vehicles

由图1和图2可知,7架临近空间飞行器自发射点开始飞行,都避开或者绕过了飞行威胁区,并且在飞行过程中尽量多且准确地路过了全部飞行任务点。

图3为飞行轨迹优化结果。由图3(a)可知，临

近空间飞行器在50 km高度发射后在铅垂面内作跳跃式机动,延长了飞行距离,能够满足飞行器编队对突防的要求。在飞行末端,飞行器迅速压低弹道,俯冲攻击目标。由图3(b)和图3(d)可知,飞行器的速度波动式减小,命中目标时最小速度均在1 500 m/s左右。飞行器在铅垂面内作跳跃式机动期间,弹道倾角波动范围在-10°～10°之间,在水平面内避障飞行和通过任务点期间,偏航角波动范围在-70°～70°之间。由图3(e)可知,飞行器的法向和侧向制导指令波动较大,这是因为临近空间飞行器需要在水平面内不断完成躲避或绕开飞行威胁区以及路过飞行任务点的飞行路径要求,且在垂直面内作跳跃式机动。由图3(c)和图3(f)可知,飞行器的总过载、最大动压和最大气动加热率均能满足飞行器的设计技术指标要求。

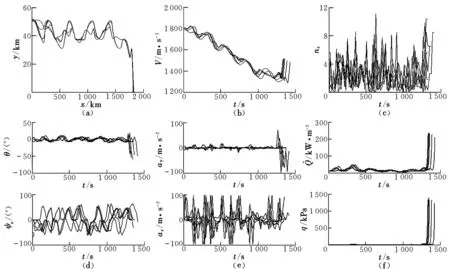
图3　飞行轨迹优化结果Fig.3　Flight trajectory optimization results

4结束语

针对众多临近空间飞行器在复杂飞行环境中的最优轨迹规划问题,本文给出了一个突防飞行方案:综合考虑避开全部飞行威胁区、路过全部飞行任务点、跳跃式滑翔飞行,同时使飞行器编队整体飞行时间最短、可靠准确地命中地面目标等性能指标。在满足飞行器各种飞行约束条件下,采用改进的动态规划法和基于共轭梯度法的多点边值问题求解算法，获得了最优控制律及相应的全部飞行器的四维飞行轨迹。

参考文献：

[1]Whang I H,Whang T W.Horizontal waypoint guidance design using optimal control[J].IEEE Transactions on Aerospace and Electronic Systems,2002,38(3):1116-1120.

[2]Yang I,Zhao Y.Efficient trajectory synthesis through specified waypoints[R].AIAA-2004-6525,2004.

[3]IBaralli F,Pollini L,Innocenti M.Waypoint-based fuzzy guidance for unmanned aircraft a new approach[R].AIAA-2002-4993,2002.

[4]nnocenti M,Pollini L,Turra D.Guidance of unmanned air vehicles based on fuzzy sets and fixed waypoints[J].Journal of Guidance,Control,and Dynamics,2004,27(4):715-720.

[5]Judd K B,McLain T W.Spline based path planning for unmanned air vehicles[R].AIAA-2001-4238,2001.

[6]Twigg S,Calise A,Johnson E.On-line trajectory optimization including moving threats and targets[R].AIAA-2004-5139,2004.

[7]Raghunathan A U,Gopal V,Subramanian D,et al.3D conflict resolution of multiple aircraft optimization[R].AIAA-2003-5675,2003.

[8]Jorris T R,Cobb R G.Three-dimensional trajectory optimization satisfying waypoint and no-fly zone constraints[J].Journal of Guidance,Control,and Dynamics,2009,32(2):551-572.

[9]晁涛,王松艳,杨明,等.基于组合优化算法的临近空间飞行器轨迹优化[J].宇航学报,2012,33(2):183-189.

[10]谢俞,刘鲁华,汤国建,等.多约束条件下高超声速滑翔飞行器轨迹优化[J].宇航学报,2011,32(12):2499-2504.

(编辑：方春玲)

Optimal trajectory planning for multiple near-space vehicles

MA Xiao-hua1,2, NAN Ying1, HUI Yao-luo1, WAN Zheng-fu2, ZHOU Sheng-long2

(1.College of Astronautics, NUAA, Nanjing 210016, China;2.Resentative Office of the Rocket Force in 307 Factory, Nanjing 210006, China)

Abstract:This paper presents a combinational algorithm of optimal 4-D trajectory planning for multiple near-space vehicles. An improved dynamic programming method and multiple-point-boundary algorithm based on conjugate gradient method are used to solve the multiple-object optimization problem. Flight numerical simulation results shown that this trajectory planning algorithm can globally optimize all trajectories for multiple near-space vehicles in real-time, considering external various environmental constraints and performance constraints of vehicles. Therefore this academic paper can be widely applied in engineering projects.

Key words:multiple near-space vehicles; flight threat zone; flight way-points; optimal flight trajectory

中图分类号：V412.1

文献标识码：A

文章编号：1002-0853(2016)02-0068-04

作者简介:马晓华(1980-)，男，山东济南人，工程师，硕士研究生，研究方向为导航、制导与控制；南英(1964-)，男，江西南昌人，教授，博士生导师，研究方向为飞行力学与控制、飞行器总体设计。

基金项目:航空科学基金资助(20140152002)

收稿日期:2015-08-13;

修订日期:2015-11-16; 网络出版时间:2016-01-10 14:13