四旋翼无人机风场扰动轨迹控制器设计
2016-05-23刘锦涛吴文海李静周思羽高丽
刘锦涛, 吴文海, 李静, 周思羽, 高丽
(1.海军航空工程学院 青岛分院, 山东 青岛 266041;2.海军航空工程学院 战略导弹系, 山东 烟台 264001)
四旋翼无人机风场扰动轨迹控制器设计
刘锦涛1, 吴文海1, 李静2, 周思羽1, 高丽1
(1.海军航空工程学院 青岛分院, 山东 青岛 266041;2.海军航空工程学院 战略导弹系, 山东 烟台 264001)
摘要:针对四旋翼无人机飞行时受风场扰动影响大的问题,以及在任务场景中对期望姿态角有约束的要求,提出了一种具有输出指令限制的自适应滑模位置控制器,将位置控制器指令转换成为期望姿态指令后,能够保证所生成的期望姿态有界,且能够有效抑制风场扰动对轨迹跟踪的影响。针对旋转矩阵形式表示的期望姿态指令,设计了一种SO(3)滑模姿态跟踪控制器,并分别用Lyapunov稳定性理论进行了分析,得到了全局稳定性的结论。最后进行了无人机在风场中盘旋爬升飞行的仿真,结果表明控制器具有较好的轨迹跟踪性能。
关键词:特殊正交群; 滑模变结构; 轨迹控制; 四旋翼
0引言
四旋翼无人机由于其结构简单、成本低、可垂直起降等优点,在军事侦察、防恐救生、环境监控、电力巡检、航拍摄影等领域得到广泛应用。在很多应用场景中,需要准确、长时间地按预定航线飞行,传统的人工操纵难以实现,因而四旋翼无人机需要精确的自动轨迹跟踪控制能力。
四旋翼无人机是一种欠驱动、多变量、强耦合的非线性系统,近年来,四旋翼无人机的轨迹控制问题得到了广泛关注。但目前研究的不足之处是未能充分考虑风扰动对四旋翼飞行器的影响。由于四旋翼无人机飞行速度相对较低,尤其在野外飞行时,外界风场的扰动对位置控制效果影响尤为显著,因而风场扰动下的高精度航迹控制是飞控系统的关键技术之一。虽然已有学者充分考虑了风扰动并设计了相应的轨迹跟踪控制器,如文献[1]将风扰动分解成常值扰动和随机扰动两部分,并设计了相应的自适应滑模轨迹控制器。但不足之处在于未考虑机动飞行时对姿态角的约束,然而四旋翼无人机在实际飞行时,为了满足挂载设备使用要求,通常需要对最大姿态角进行限制。
针对以上问题,本文将四旋翼无人机非线性模型分解成位置与姿态两个级联子系统。位置控制器主要针对阵风对四旋翼无人机轨迹跟踪的影响,且跟踪时对期望姿态角的约束限制,设计了一种具有饱和滑模面的自适应滑模位置控制器,能够保证所生成的期望姿态角有界,抑制风场扰动对轨迹跟踪的影响。另外,位置控制器利用滑模控制迅速补偿未知扰动的影响,在线估计常值风的影响并进行预先补偿,缓解了滑模控制开关所产生的不利影响。最终在期望飞行速度和风扰动的上界满足一定假设的条件下,实现稳定的轨迹跟踪性能。
1模型建立
本文研究的四旋翼无人机结构如图1所示。图中:Ow1w2w3为惯性参考坐标系;Ob1b2b3为机体参考坐标系。
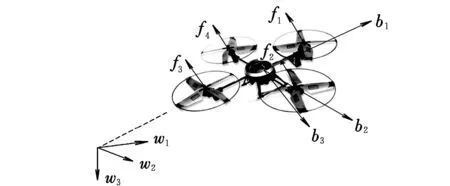
图1 四旋翼无人机模型Fig.1 Model of quadrotor UAV
假设以合力f和力矩矢量M作为四旋翼无人机系统的控制输入量[1],则四旋翼无人机的运动方程可表示为:
(1)

在实际飞行中,作用在四旋翼飞行器上的通常是紊流风场[3]。本文仅考虑常值风和随机风的影响。
2问题描述
设给定轨迹跟踪的指令:位置xd(t),速度vd(t),姿态矩阵Rd(t),角速度Ωd(t)。 定义误差状态量如下:
(2)
(3)
(4)
得到位置误差模型:
(5)
式中:h(·)=u-(f/m)Rb3为位置误差模型与姿态误差模型之间的耦合部分。由姿态误差模型式(3)和式(4)得到相应的姿态误差模型为:
(6)
其中:
(7)
(8)
3控制器设计及稳定性分析
3.1总体设计思路
考虑到四旋翼无人机模型耦合关系复杂,直接分析其全局稳定性比较困难[4],因而可进行系统解耦,分别设计姿态控制器使得系统的姿态稳定,设计位置控制器实现对飞行器质心的位置控制。如文献[5]使用了backstepping方法,将四旋翼无人机复杂的非线性系统分解成位置子系统和姿态子系统,并分别进行Lyapunov函数的选取与控制器的设计。但考察式(5)和式(6)可发现,系统并不满足严格反馈规范型要求,无法直接使用backstepping设计方法。为此,文献[6-7]给出了与式(9)相似的一种稳定性判据:
(9)
文献[4]对形如式(9)的四旋翼无人机误差方程进行了位置-姿态解耦控制设计,分析了子系统和耦合部分的性质,得到了闭环系统的全局稳定条件。在此结构基础上,本文所设计的控制系统结构如图2所示。分别设计位置控制器和姿态控制器,由于四旋翼无人机自身欠驱动的动力学特点,四旋翼无人机的平移运动需通过改变姿态来实现,需要增加一个姿态提取算法由位置控制器输出的平移加速度指令u生成期望姿态Rd(t)和期望角速度Ωd(t)。
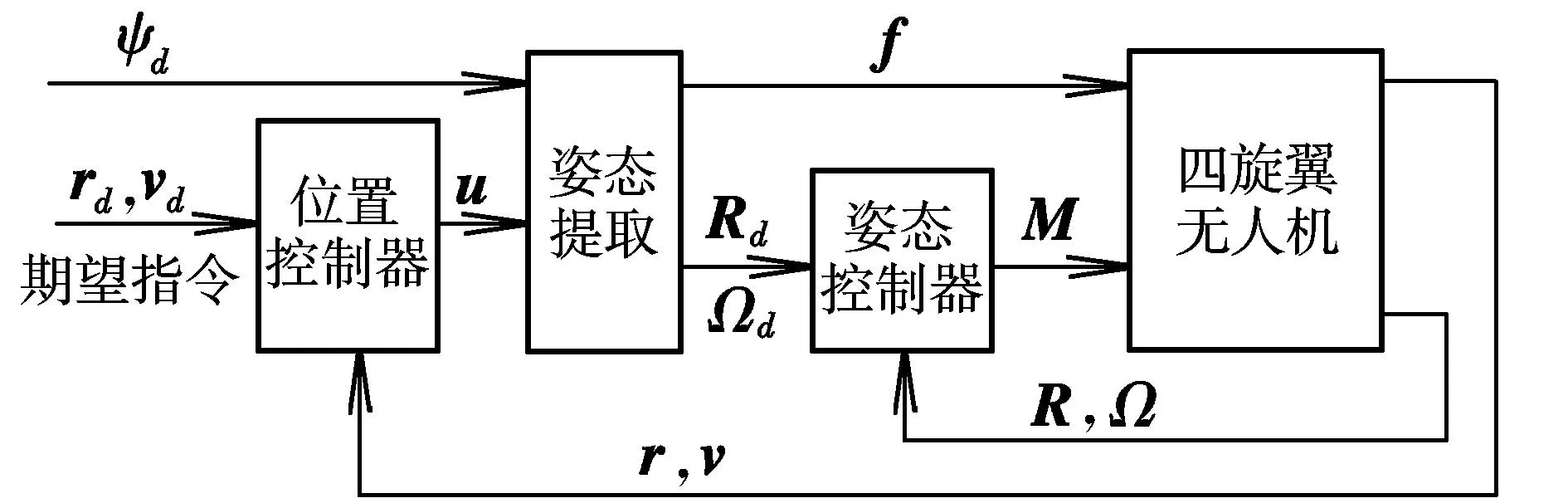
图2 四旋翼无人机控制系统结构图Fig.2 Structure of quadrotor UAV control system
3.2滑模位置控制器设计
设计滑模面:
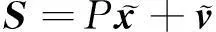
(10)
设饱和函数χ(x)=[σ(x1),σ(x2),σ(x3)]T,考虑到水平运动和升降运动的不同,分别设计其饱和函数为:
设计抗饱和位置自适应滑模控制器为:
(11)
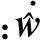
提出如下假设:
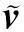
以下证明位置子系统的稳定性。
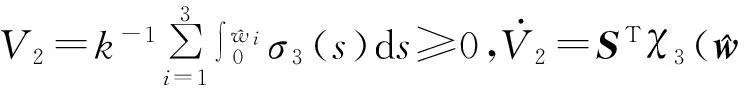
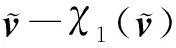
ST‖Δx‖-ksSTsgn S
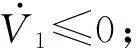
4姿态控制器设计
4.1期望姿态指令生成
将期望的升力矢量u=[u1,u2,u3]T投影至机体轴b3得到合力输出f=FdesRb3=muRb3,则期望的机体轴b3,des的方向与Fdes的方向重合,有:
设期望的偏航角为ψd,有:
得到:
假设b3,des×byaw,des≠0(等于0为唯一奇点),则由b1,des,b2,des,b3,des可得到Rd。
当对飞行器最大姿态角及升降加速度有限制要求时,可通过设置饱和函数上界来限制虚拟指令的u=[u1,u2,u3]T的范围。
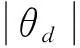
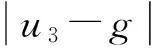
当u=[u1,u2,u3]T满足约束方程(12)时,则满足约束1和约束2:
(12)
为简化分析,假设升降加速度较小时,可将约束方程(12)适当放宽:
(13)
因此饱和函数及参数kp选取时应满足:
(14)
4.2滑模姿态控制器设计与稳定性分析
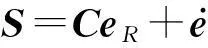
(15)
其中:
K1=diag{k11,k12,k13}
K2=diag{k21,k22,k23}
k1i,k2i>0(i=1,2,3)
(16)
其中:
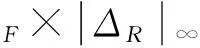
5仿真分析
设飞行器质量m=0.455 kg,转动惯量矩阵J=diag{0.43,0.43,1.02}×10-2kg·m2。初始位置、速度、姿态、角速度均为0。仿真时长设定为30 s。轨迹跟踪指令为:xd=sin(0.5t),yd=cos(0.5t),
zd=-2t。
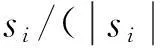
设计盘旋上升运动指令,期望轨迹与实际飞行轨迹如图3所示。在初始阶段,受风的影响,轨迹偏差较大,后期跟踪效果不断变好。仿真曲线如图4所示,为便于观察分析,用欧拉角表示三轴期望姿态角。风扰动估计曲线表明,风扰动能够迅速收敛(见图4(f))。所生成的合力控制指令如图4(e)所示。最终无人机能够在具有不确定风扰动下跟踪预定轨迹,且所生成的期望姿态有界。
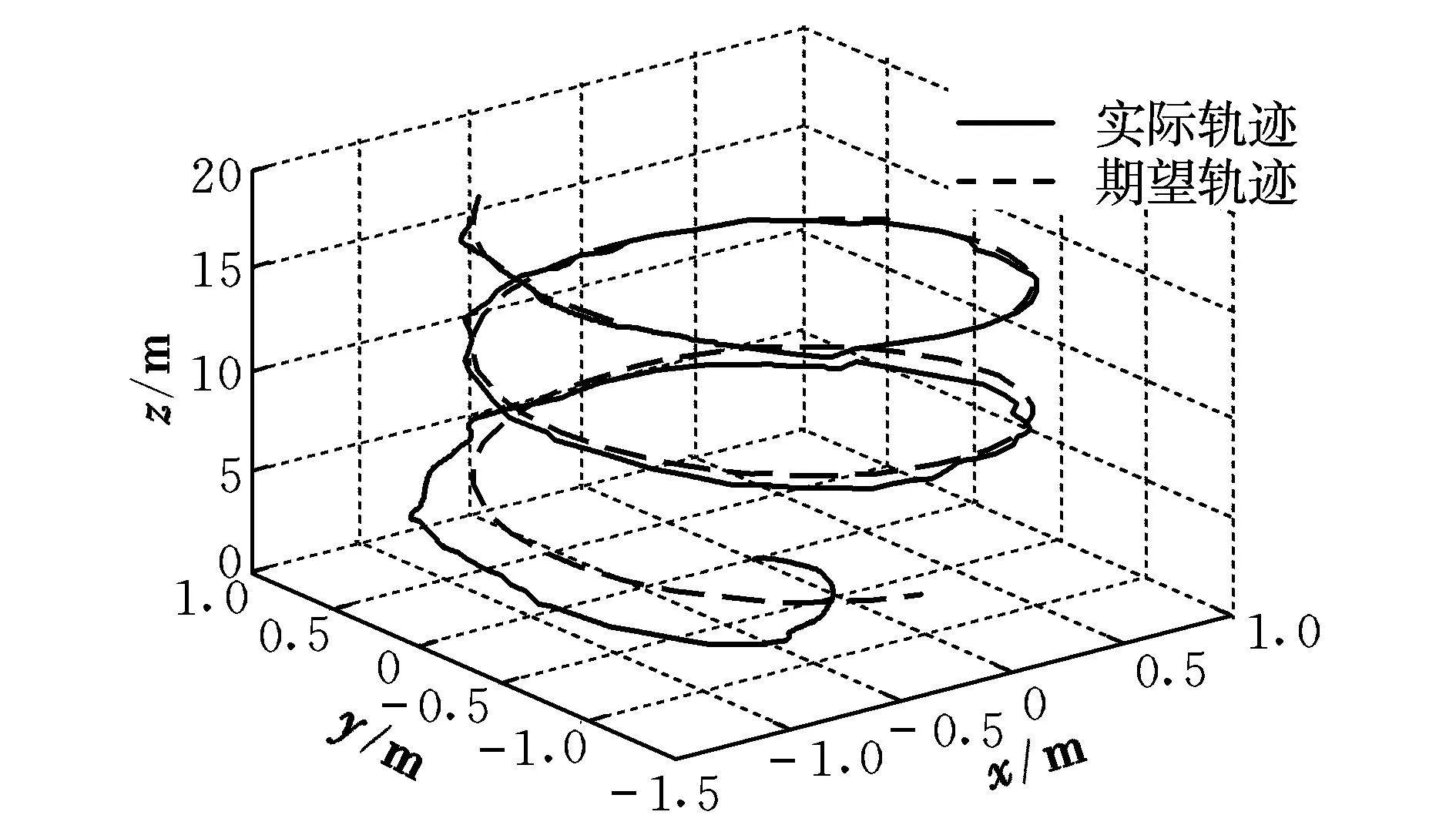
图3 期望轨迹与实际轨迹Fig.3 Desired trajectory and actual trajectory
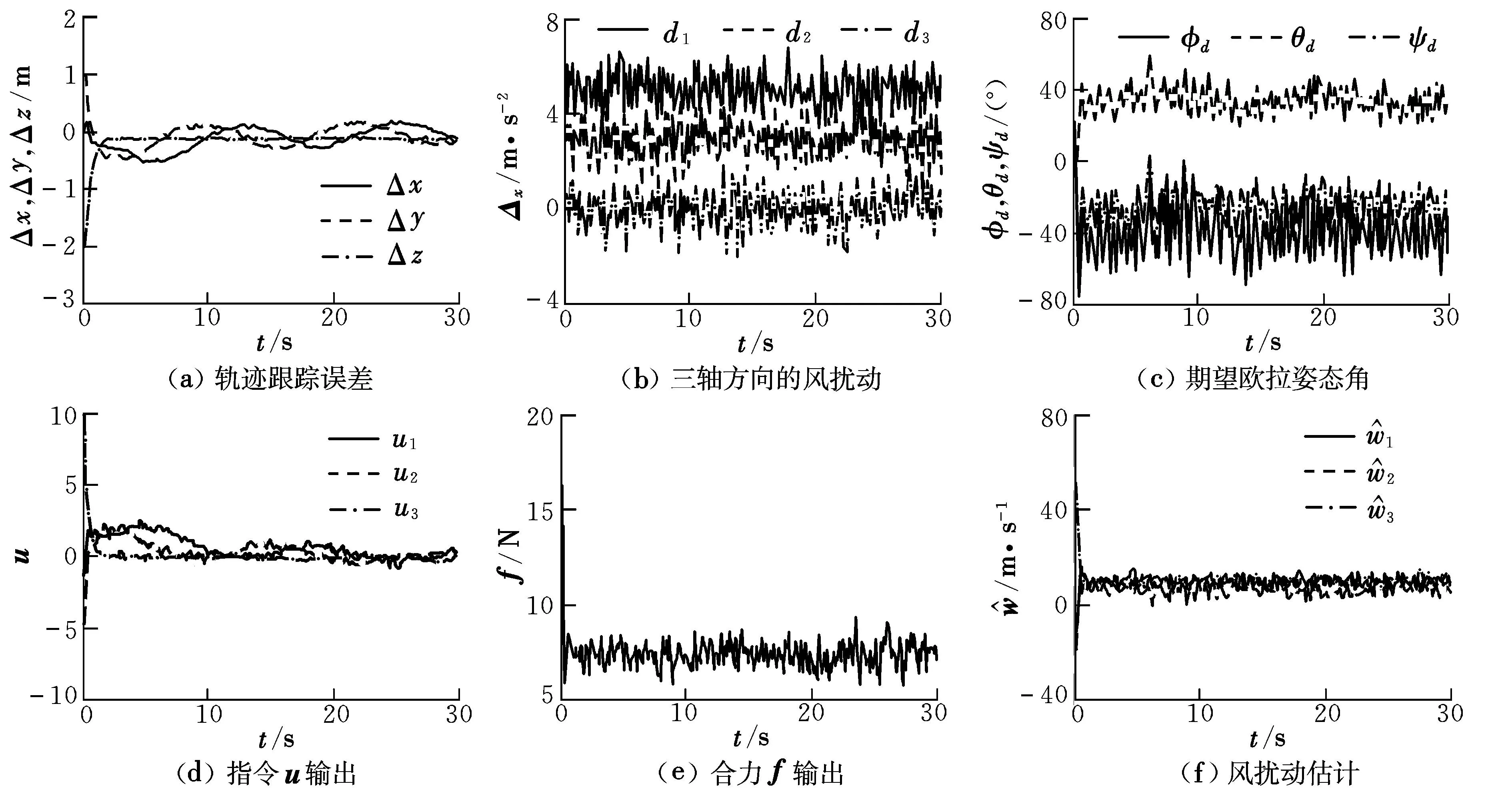
图4 仿真曲线Fig.4 Simulation curves
6结束语
本文主要针对阵风对四旋翼无人机的影响设计了一种滑模自适应轨迹控制器,并进行了稳定性证明。轨迹控制器利用滑模控制的开关特性能够迅速补偿未知扰动的影响,能够在线估计常值风的影响并进行预先补偿,同时缓解了滑模控制颤振的不利影响,最终实现了在阵风扰动的情况下仍具有较好的轨迹跟踪性能。并通过饱和滑模面的设计,保证了所生成的期望姿态角有界,满足了任务场景中对期望姿态角有约束的要求。最后通过仿真试验表明,所提出的滑模变结构控制方法具有快速而良好的轨迹跟踪性能。本文所提出轨迹控制器可应用于类似的运动控制系统中,具有良好的可推广性。
参考文献:
[2]吴文海,刘锦涛,李静,等.四旋翼无人机SO(3)快速终端滑模姿态控制器设计[J].电光与控制,2015,22(11):6-10.
[3]何勇灵,陈彦民,周岷峰.四旋翼飞行器在风场扰动下的建模与控制[J].中国惯性技术学报,2013,21(5):624-630.
[4]李光春,王璐,王兆龙,等.基于四元数的四旋翼无人飞行器轨迹跟踪控制[J].应用科学学报,2012,30(4):415-422.
[5]Bouabdallah S,Siegwart R.Backstepping and sliding-mode techniques applied to an indoor micro quadrotor[C]//International Conference on Robotics and Automation.Spain:ICRA,IEEE,2005:2247-2252.
[6]Panteley E,Lefeber E,Loria A,et al.Exponential tracking control of a mobile car using a cascaded approach[C]//Proceedings of the IFAC Workshop on Motion Control.Vanderhaegen,France,1998:221-226.
[7]Panteley E,Loria A.On global uniform asymptotic stability of nonlinear time-varying systems in cascade[J].Systems & Control Letters,1998,33(2):131-138.
(编辑:方春玲)
Trajectory controller design for quadrotor UAVs on wind field disturbance
LIU Jin-tao1, WU Wen-hai1, LI Jing2, ZHOU Si-yu1, GAO Li1
(1.Qingdao Branch, NAEI, Qingdao 266041, China;2.Department of Strategic Missile Engineering, NAEI, Yantai 264001, China)
Abstract:For the problems of wind field disturbance in quadrotor UAVs flight, and the constraint of attitude angle in the task scenario, this paper proposes a self-adaptive sliding mode position controller with output constrains。With the position controller transferred to desired attitude command, the controller could guarantee that the created desired attitude has a boundary, and could effectively inhibit the wind field influence on trajectory tracking. For the desired attitude represented by the rotation matrix, a SO (3) sliding mode attitude tracking controller is designed. And the stability is analyzed by Lyapunov stability theory, the resulted conclusion is global. Finally, the simulation of spiral climb in wind field has been carried on, the results show that the controller has good trajectory tracking performance.
Key words:special orthogonal group; sliding mode variable structure; trajectory control; quadrotor
中图分类号:V279; V249
文献标识码:A
文章编号:1002-0853(2016)02-0047-04
作者简介:刘锦涛(1981-),男,山东莱阳人,工程师,博士研究生,研究方向为无人机控制。
收稿日期:2015-06-29;
修订日期:2015-11-23; 网络出版时间:2016-01-10 14:13
