型钢-混凝土组合结构地震恢复力模型研究

龚倩倩

(长江大学城市建设学院，湖北 荆州 434023)

赵清民

(荆州市江陵银龙水务有限公司，湖北 荆州 434000)



型钢-混凝土组合结构地震恢复力模型研究

龚倩倩

(长江大学城市建设学院，湖北 荆州 434023)

赵清民

(荆州市江陵银龙水务有限公司，湖北 荆州 434000)

[摘要]为了研究型钢-混凝土组合结构的抗震性能，对地震恢复力模型进行了研究。通过比较国内外学者已提出的恢复力模型，分析了其优势与不足，得出刚度退化三折线恢复力模型适用于型钢-混凝土组合结构的恢复力模型研究中。在该恢复力模型的基础上，考虑到正反向弹性刚度不一致，提出了改进恢复力模型，并给出了模型建立的内容、数据处理与拟合方法以及拟合时加载与卸载规则。通过分析研究已有刚度退化三折线恢复力模型的研究结果，并对比各试验模型，提出引入修正系数，建立一个适用所有型钢-混凝土组合结构的参考恢复力模型，为型钢-混凝土组合结构的地震恢复力模型研究提供参考依据。

[关键词]型钢-混凝土组合结构；刚度退化三折线恢复力模型；建议恢复力模型；修正系数

近年来由于世界各地地震频繁发生，带来的人力、财力及物力损失不计其数，因此人们把抗震研究作为建筑结构性能研究的重中之重。国内外学者先后对型钢-混凝土结构展开了大量低周往复荷载试验，大多学者根据研究分析试验滞回曲线和骨架曲线得出的相关指标对结构的抗震性能进行分析，而少数学者通过建立的恢复力模型进行分析。目前对型钢-混凝土组合结构的恢复力模型研究没有具体的建立步骤与数据处理方法，为得出一套系统的符合实际情况的型钢-混凝土组合结构恢复力模型，通过比较分析国内外已提出的恢复力模型的优缺点，考虑包辛格效应[1]，提出了改进刚度退化三折线恢复力模型，并给出了改进模型建立的内容、方法与步骤。少数采用刚度退化三折线恢复力模型进行恢复力特性试验研究的结果表明，各试验拟合得出的刚度退化规律公式中各参数相近但不一致，为得出一个统一的公式，提出了引入相关修正系数，建立一个适用所有型钢-混凝土组合结构的刚度退化规律参考公式，以供所有型钢-混凝土组合结构进行非线性抗震分析。

1曲线与折线形恢复力模型

图1　兰伯格-奥斯古德模型

恢复力模型研究可分为材料的恢复力模型、构件的恢复力模型和结构的恢复力模型3个层次。由于材料、结构或构件的实际滞回曲线和恢复力曲线十分复杂，国内外许多学者先后开展了大量材料层次的恢复力研究，并逐渐过渡到构件、结构层次的恢复力模型研究。已提出的恢复力模型大致可分为2大类，即曲线形恢复力模型和折线形恢复力模型[2]。

1.1曲线形恢复力模型

曲线形恢复力模型能体现加载、卸载过程中刚度是连续变化的事实，但其刚度曲线形变化过程比较复杂，难以得出直观的刚度退化公式。其典型代表是兰伯格-奥斯古德模型[3]，如图1所示。该模型由屈服荷载Py及其对应的屈服位移Δy、形状指数γ这3个基本参数确定的骨架曲线模型，其模型曲线定义为：

(1)

式中，η为常系数，由材料的特性决定；γ为形状指数，当γ=1时，为线弹性状态，当γ趋于无穷时，骨架曲线也逐渐趋向理想弹塑性状态。

该模型虽能体现刚度连续变化，较为符合工程实际，但其缺点在于常系数η与形状指数γ针对同一组合结构或不同的组合结构在不同因素及环境作用下难以得出明确的数值或范围，现有建筑规范也未给出其相关取值的参考或规定。

1.2折线形恢复力模型

折线形恢复力模型是由若干折线段构成，能反映结构在强度和刚度退化、开裂和屈服、裂缝闭合等阶段刚度变化特性的数学模型，已提出的折线形恢复力模型有刚度退化二线型模型和刚度退化三线形模型。

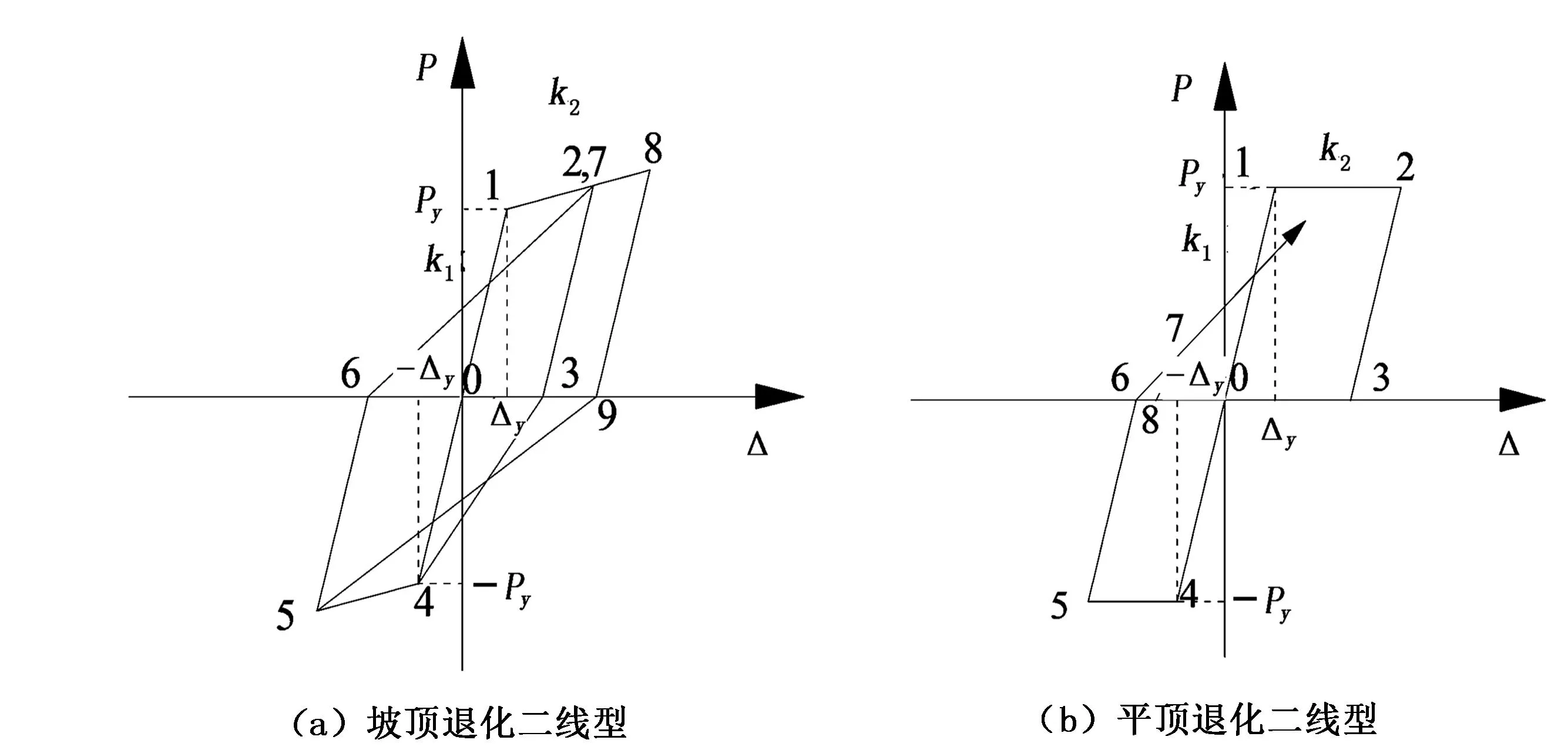
图2　刚度退化二线型模型

1)刚度退化二线型模型刚度退化二线型模型是用两段折线来描述正反向加载路径，并考虑了刚度退化及屈服后硬化效应所构建的模型。根据是否考虑屈服后的硬化情况，又可将二线型恢复力模型分为刚度坡顶退化二线型和刚度平顶退化二线型，如图2所示。图2中， k1、k2分别表示弹性刚度与弹塑性刚度；第一个折点1为屈服点，对应的荷载与变形分别用Py、Δy表示。典型刚度退化二线型模型有Bi-linear模型、Clough模型[4]等。

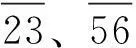
图3　刚度退化三线型模型

2) 刚度退化三线型模型刚度退化三线型模型是在刚度退化二线型模型的基础上，考虑屈服后卸载刚度发生退化，用三段折线反映正反向加载、卸载规律的模型。与刚度退化二线型模型类似，根据是否考虑结构屈服后的硬化情况，又可将其分为刚度坡顶退化三线型和刚度平顶退化三线型，如图3所示。图3中，OA(OA′)、AB(A′B′)、BC(B′C′)段折线分别表示弹性阶段、屈服阶段、破坏阶段。A(A′)、B(B′)、C(C′)点分别表示屈服点、极限点、破坏点。典型三线型模型有Takeda[5]模型、Park三折线模型等。

2改进恢复力模型

从上述两大类模型研究可知坡顶刚度退化三折线恢复力模型更符合实际。因此，在该模型基础上，考虑到屈服前正反向弹性刚度不一致，提出改进刚度退化三折线恢复力模型。恢复力模型建立的方法通常有理论计算法、系统识别法与试验拟合法3种。对结构构件的恢复力特性的研究，通常都是基于试验数据及其滞回曲线的滞回规则进行的。因此，采用试验拟合法建立改进刚度退化三折线恢复力模型。下面给出试验拟合法建立改进三折线骨架曲线模型的过程。

图4　正反向加载与卸载规律

2.1骨架曲线模型

将各试验滞回曲线上正反向数据点分别除以该滞回曲线正反向最大极限荷载对应坐标的绝对值，得到无量纲化数据点。分别将试验骨架曲线中弹性段、屈服段、破坏段的所有数据进行线性回归，即可得到图4中正反向弹性刚度不一致，用C′B′A′OABC表示的三折线骨架曲线模型，并得出各折线段线性方程。图4中，OA、OA′线段斜率分别表示正、反向初始相对弹性刚度；+Pu与-Pu、+Δu与-Δu分别表示正、反向极限荷载及其对应的位移。3个特征点分别为屈服点A与A′，荷载峰值点B与B′，破坏点C与C′。

2.2刚度退化规律

滞回曲线上每个滞回环可分为正向加载段、正向卸载段、反向加载段与反向卸载段4部分，将各1/4环数据点线性回归即可得到一个正向加载刚度、正向卸载刚度、反向加载刚度与反向卸载刚度，各部分刚度总数由滞回曲线数与各滞回曲线滞回环数决定。以各向加载与卸载刚度分别除以各向初始相对弹性刚度为纵坐标点，以对应的各向加载与卸载位移分别除以各向加载点位移、极限点位移为横坐标点，运用Origin软件进行对数拟合即可分别得到各向加载、卸载刚度退化公式。

2.3正反向加卸载规律

非线性回归出正反向加载与卸载刚度退化公式后，即可按照图4所示的正反向加载与卸载规律进行滞回曲线拟合，得到模型滞回曲线。现给出加载与卸载规律如下：

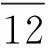
将按照上述正反向加载与卸载规律得到的模型滞回曲线的各环最大荷载点连接起来，即得到模型骨架曲线，将模型曲线与试验曲线进行比较，其吻合度较好，则证明该恢复力模型建立过程和回归方法正确，考虑因素全面，可为型钢-混凝土结构抗震性能研究的提供参考依据。

3型钢-混凝土结构改进恢复力模型

型钢-混凝土组合结构包括型钢混凝土和钢管混凝土等组合结构，其中型钢混凝土结构又分为对称配钢型钢混凝土结构、非对称配钢型钢混凝土结构；钢管混凝土结构又分为圆钢管混凝土结构、矩形钢管混凝土结构和多边形钢管混凝土结构等,如图5所示。目前少数学者分别针对型钢混凝土结构、钢管混凝土结构进行了恢复力模型试验研究，各自得出了对应的参数与恢复力模型。郭子雄等学者通过开展6个1/2比例的型钢混凝土框架柱试件低周往复加载试验，考虑位移延性和轴压比，建立了三折线骨架曲线模型，试验结果表明，采用建议方法确定的恢复力模型与试验结果较为接近，能较好地模拟延性和轴压比对抗震性能的影响[6]。王彦斌等为研究非对称配钢型钢混凝土柱的抗震性能，对12个T形配钢和12个L形配钢柱进行了恢复力特性试验研究，提出了P-Δ恢复力模型，将提出的恢复力模型用直线简化后基本上能与外包骨架曲线较好吻合，能为非对称配钢型钢混凝土柱弹塑性反应分析提供参考价值[3]。马凯泽等通过理论回归分析23根方钢管高强混凝土柱反复荷载作用下的试验结果，提出方钢管高强混凝土柱的恢复力模型，研究结果表明按建议恢复力模型计算的骨架曲线与试验骨架曲线符合较好，说明该模型可对结构进行非线性动力分析[7]。徐亚峰等对5个钢骨-钢管混凝土柱进行了低周反复荷载作用下受力特性试验研究，提出了考虑含骨率和轴压比、延性、耗能和强度、刚度退化等影响因素的多折线型钢骨-钢管混凝土柱恢复力模型，为钢骨-钢管混凝土柱的弹塑性时程分析提供了参考[8]。杨炳等基于3根碳纤维布加固方钢管柱低周反复荷载试验结果，建立了碳纤维布加固方钢管混凝土柱三折线骨架曲线模型，比较试验骨架曲线与模型骨架曲线，两者较为符合，可供碳纤维布加固钢管混凝土柱及其结构非线性地震反应及抗震加固应用[9,10]。

图5　型钢-混凝土组合结构不同截面

分析比较以上各学者所得提出的恢复力模型，得出所有模型均采用刚度退化三折线恢复力模型，且拟合所得模型曲线与试验曲线相比较，吻合度均较好。所有试验所得模型的正反向刚度退化规律公式中，各参数只有些许差别，于是提出引入修正系数ψ、φ、θ，建立一个适用所有型钢-混凝土组合结构的刚度退化规律参考公式：

(2)

4结论

1)为了对型钢-混凝土组合结构的地震恢复力模型进行研究，分析总结研究国内外学者提出的各种恢复力模型优缺点，得出刚度退化三折线恢复力模型最符合实际工程条件。

2)在刚度退化三折线恢复力模型的基础上，考虑屈服前正反向弹性刚度不一致因素，提出改进刚度退化三折线恢复力模型。

3)参考已有恢复力模型影响因素及其建立过程，给出了改进恢复力模型的建立过程，数据处理与拟合方法等较系统全面的模型建立步骤。

4)提出了引入3个修正系数ψ、φ、θ，建立一个适用所有型钢-混凝土组合结构的统一公式。为得出3个系数具体数值，需要获取已有相关试验数据，同时进行大量不同型钢-混凝土组合结构构件试验，通过拟合得出，以便今后对型钢-混凝土组合结构进行滞回特性分析与地震恢复力特性分析。

[参考文献]

[1]郭子雄,杨勇.恢复力模型研究现状及存在问题[J].世界地震工程,2004,20(4):47～51.

[2]张新培.钢筋混凝土抗震结构非线性分析[M].北京:科学出版社,2003.

[3] 王彦斌.非对称配钢型钢混凝土柱抗震性能试验研究[D].荆州:长江大学,2012.

[4]刘义.型钢混凝土异形柱框架节点抗震性能及设计方法研究[D].西安:西安建筑科技大学,2009.

[5]Takeda T, Sozen M A，Nielson N N.Reinforced concrete response to simulated earthquakes[J].Journal of Structural Division, ASCE,1970,96(ST12):2557～2572.

[6]郭子雄,张志伟,黄群贤,等.型钢混凝土柱恢复力模型试验研究[J].地震工程与工程振动,2009,29(5):79～85.

[7]马凯泽,梁兴文,李斌.方钢管高强混凝土柱恢复力模型研究[J].世界地震工程,2011,27(1):54～59.

[8]徐亚峰,赵敬义,李宁,等.钢骨-钢管混凝土柱恢复力模型[J].沈阳建筑大学学报(自然科学版)，2009,25(3):482～485.

[9]赵斌,杨炳,卢梦潇,等.碳纤维布加固方钢管混凝土柱恢复力模型研究[J].长江大学学报(自科版),2015,12(25):52～57.

[10]赵鸿铁.钢与混凝土组合结构[M].北京:科学出版社,2001.

[编辑]计飞翔

[文献标志码]A

[文章编号]1673-1409(2016)10-0047-05

[中图分类号]TU398

[作者简介]龚倩倩(1989-)，女，硕士生，现主要从事钢与混凝土组合结构方面的研究工作； 通信作者，赵清民，825493256@qq.com。

[基金项目]国家自然科学基金项目(51108041)。

[收稿日期]2016-01-01

[引著格式]龚倩倩，赵清民.型钢-混凝土组合结构地震恢复力模型研究[J].长江大学学报(自科版)，2016,13(10)：47～51.