考虑不确定性成本的含风电场群电力系统短期优化调度
2016-05-23曲正伟王京波王云静
曲正伟,王京波 ,张 坤 ,王云静 ,郑 磊
(1.燕山大学 电力电子节能与传动控制河北省重点实验室,河北 秦皇岛 066004;2.国网湖北省电力公司检修公司,湖北 武汉 430000)
0 引言
随着能源危机的加剧和环境问题的日益突出,风电作为一种清洁可再生能源成为能源供应的重要选择。然而,随着风电基地的集约化建设,同一区域风电场密度和并网容量增加,风速的时空分布特性给电力系统的稳定运行和调度计划的制定带来前所未有的挑战。
含风电场的电力系统经济调度问题,关键在于考虑风电功率的不确定性对调度决策的影响。以往的研究中很少考虑风电功率的不确定性对旋转备用容量的额外要求,同时也经常忽略相邻风电场之间的空间相关性,这必然会影响调度结果的客观性。研究初期,常通过增加一定比例的旋转备用容量,将其转化为传统的确定性调度问题,但由于没有定性分析风电的不确定性对调度的影响,该方法容易得出保守或者冒进的决策方案,经济性和安全性无法得到有效保证[1]。 文献[2-3]基于模糊集理论,通过定义隶属度函数来处理风电的不确定性,但其所得调度决策方案却受制于主观因素。文献[4-6]在优化模型中引入机会备用约束对风电系统的短期优化进行研究,但该方法难以确定机会备用约束的最佳置信度。文献[7-9]在短期经济运行中,将“失负荷”和“弃风”惩罚成本纳入经济性考量,或者在目标函数中加入发电成本期望等风险度量项,对更广意义的电力系统优化进行了有益探索。然而上述模型均忽略了各风电场之间的风速相关性,从而降低了调度方案的准确度。同一区域的风电场由于受同一风源的影响,各维风速之间具有一定的时空分布关系。为有效考虑风速的相关性因素,文献[10-11]通过协方差矩阵变换法或Nataf逆变换技术,得到不同风电场之间具有线性相关的风速分布样本,并分析了风速的线性相关性对概率潮流计算的影响。然而,风速的分布具有不对称的厚尾特性,使得风电出力的概率分布也呈现出相应的厚尾特性,从而导致线性相关系数具有一定的局限性,不加分析地使用该指标可能会导致错误的结论。鉴于此,有学者提出运用Copula函数构建电力系统随机变量联合概率分布的思想,并采用Copula函数描述了离岸和近岸风力发电以及风电示范工程中相邻风电场的时空分布特征,对含风电场群的系统优化问题进行了探索,取得了较好的效果[12-13]。
本文首先结合Copula函数生成具有已知时空分布特性的多维风电功率的场景空间。在优化模型中,将风电计划出力作为优化变量,并在目标函数中加入因风电计划出力偏差导致的“电能短缺”和“电能盈余”等不确定成本项,从经济性的角度量化了风电不确定性带来的成本的增加。通过对风电功率和负荷等随机变量的场景运算,并采用改进的量子粒子群优化(IQPSO)算法求解,提高了模型求解速度并准确直观地反映出系统的风险水平和最佳置信度,有助于调度人员制定更加经济、灵活、合理的调度方案。
1 多维风速的时空分布特性分析
1.1 Copula函数定义
Sklar定理[12-14]指出,任何联合分布函数都可用描述其随机性的边缘分布Fi(xi)以及描述相关结构的Copula函数来刻画。即存在这样一个Copula函数 C(F1(x1),F2(x2),…,Fn(xn)),使得:

其中,F(x1,x2,…,xn)为随机变量 x1、x2、…、xn的联合分布函数。
1.2 Copula函数的构造
本文以某相邻风电场(W1和W2)风速样本为研究对象,简述构建Copula函数模型的步骤如下。
a.确定风速的边缘分布。实测数据表明,各风电场风速的短期概率分布特性可用正态分布来描述,即:

其中,Fi,t(x)为风电场 i在 t时段的风速概率分布函 数 ;和分别为t时段预测风速平均值和标准差。
b.Copula 函数的选择与评估。 令 U=F1(x)、V=F2(x),由Copula函数的性质可知,对变量进行严格单调增变化时,由Copula函数导出的相关性测度不会改变[13]。因此,不同时段的风速Copula函数具有相同的相关性结构,因此根据各风电场的历史风速选择合适的Copula模型。图1所示为U和V的历史频率直方图,它是(U,V)联合概率密度的估计。由于其具有明显的对称性,通过分析常用的Copula函数及其特点可知,选择Gau-Copula或t-Copula函数分析W1和W2的风速时空分布特性比较合适。其Copula 概率分布函数分别为[12-13]:

其中,u和v为Copula函数的三维变量;ρ为变量间的线性相关系数;k为自由度;Φ-1(·)为标准正态分布函数的逆函数;tk-1(·)表示自由度为k的t分布函数的逆函数。

图1 W1和W2联合频率直方图Fig.1 Joint frequency histogram of W1and W2
为进一步比较所选Copula函数的优劣,引入欧氏距离的概念,其定义式如下[12-13]:

其中,为 EMC 函数,是实际分布函数的一个逼近;C(ui,vi)为 THC 函数。
c.Copula函数的参数估计。极大似然法是一种经典的参数估计方法,在数理统计和参数估计领域有广泛的应用。该方法可分为精确法和两阶段法,虽然精确法能够同时估计模型中的所有参数,但由于Copula模型参数过多而不利于最大似然函数的寻优,因此本文选用两阶段极大似然法估计Copula模型的参数,因而将参数估计的过程分解为两步。
第一步:估计出边缘分布函数的参数。

第二步:估计出Copula函数中的相关参数。

根据W1和W2的历史风速数据,通过参数估计得到各Copula模型的相关参数,结果如表1所示。显然,二元t-Copula函数的欧氏距离更小,由此认为t-Copula函数在描述多维风速的时空分布特性方面具有更好的适用性。图2给出了其概率密度函数图。

表1 各Copula函数参数估计结果Table 1 Parameter estimation results of different Copula functions

图2 W1和W2联合概率密度函数图Fig.2 Joint probability density function of W1and W2
2 系统运行风险建模
一方面,由于风电的并网改变了系统的电源分布,因而系统的潮流分布也要发生巨大变化,这使得原有的系统面临线路过载的风险,即[12]:

其中为线路过载风险指标;Nline为系统中线路数量;Prob{·}表示事件发生的概率为各线路的传输功率极限;pline,l为线路l流过的功率,可通过直流潮流模型求取,表达式如下所示。

其中,θ为各节点电压相位矢量;θi和θj为线路两端的相位;B为系统电纳矩阵;Pg、Pw和Pload分别为各节点的常规机组出力、风电出力和负荷组成的向量。
另一方面,由于《可再生能源法》明文规定风电应全部上网,因此风电功率的随机性必然使得系统的旋转备用需求增加。在运行过程中,系统将不可避免地面临因正负旋转备用不足而导致的系统“切负荷”或者“弃风”的危险。因此,本文以“切负荷”和“弃风”概率作为系统的运行风险指标,即:

其中,为风电计划出力;Δpload为系统负荷预测误差,通常采用均值为0的正态分布来描述;pw为实际风电总功率;Su和Sd分别为系统能提供的最大正、负备用容量,表达式如下所示。

其中,Ng为常规机组台数和分别为第 i个常规机组的上、下爬坡速率;T10为旋转备用响应时间,取值10 min;分别为常规机组i的最大和最小出力极限。
imax和为常规机组i在t时段的有功出力的上、下限,即:

其中,T60为单位运行时间,在本文中取1 h。
由于系统负荷预测误差Δpload和实际风电总功率均为随机变量,为方便分析,本文将两者之和定义为等效风电出力pe,即:

其中,Nw为风电场群中的风电场数量。
3 考虑不确定成本的电力系统优化调度模型
3.1 确定性成本建模
电力系统中确定性成本即为常规机组的燃料成本,其单时段的火电机组成本函数通常用该机组有

其中,di、ei为阀点效应系数。
3.2 不确定成本建模
由上文可知,各时段的风电出力均为服从一定概率分布的随机变量,而参与优化的各时段风电计划出力是一个确定值。如图3所示,利用将风电功率的概率密度曲线一分为二,其左边和右边即分别为风电出力短缺和盈余情况。功出力的二次函数表示,即:

其中,ai、bi和 ci为火电成本系数。
此外,汽轮机进气阀开启瞬间出现的拔丝现象会在机组耗量曲线上产生阀点效应,从而造成能耗成本的增加,即[5]:

图3 风电功率短缺与盈余概率分布Fig.3 Shortage and surplus probability distribution of wind power output
如果计划出力偏高,需调用常规机组的备用容量来补偿风电出力的不足,则造成能源消耗成本增加;同理,当计划出力偏低,需调用负备用容量补偿风电出力的盈余,则造成风能资源的损失。因此,本文定义的系统不确定成本为因电能短缺和电能盈余而导致的运行成本的增加,即:

其中,为电能短缺成本,反映了正备用调用成本或备用不足造成的停电损失;为电能盈余成本,反映了负备用调度成本和风能浪费造成的环保效益的降低。
a.电能短缺成本。
电能短缺时,风电场负效率运行,系统必须通过增加旋转备用容量出力甚至是切掉部分负荷的方式达到维持系统稳定的目的。电能短缺造成的成本增加主要取决于风电场实际运行情况下对风电出力不足的概率、正备用需求以及旋转备用容量调度的难易程度等指标的量化[15]。因此,风电出力短缺概率成本如下式所示:
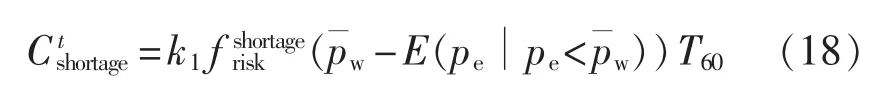
b.电能盈余成本。
电能盈余时,系统必须通过减小常规机组出力或弃风的手段维持系统功率平衡。与电能短缺成本类似,影响该项成本的因素包括:风电场出力盈余情况发生的概率、负旋转备用需求量以及负旋转备用的调度难易程度[15]。因此,特定风电计划出力情况下,相应的电能盈余成本可表示为:

式(18)和(19)中和分别为风电场出力短缺和出力盈余的概率;k1和k2分别为电能短缺和电能盈余成本系数,其大小的厘定参见文献[16]。
3.3 目标函数
含风电场电力系统经济调度的目标是在优先考虑风电并网的基础上合理分配常规机组出力使系统获得最大的经济和社会效益。

3.4 约束条件
a.功率平衡约束:

b.风电场出力计划约束:

c.常规机组出力约束:

d.常规机组爬坡约束:

e.系统运行风险约束。
在系统运行中,须将风险指标约束在允许的范围内以保证系统的安全稳定,并避免大量的弃风。

其中,Nd为系统负荷节点个数为第 j节点的负荷预测值;T为一个调度周期;wmax,j为风电场j装机容量;μ1、μ2和μ3为各风险指标的风险阈值,通常取值 0~10% 。
4 模型处理与求解
4.1 基于场景运算的机会约束处理
该模型中含有机会约束条件和等效风电出力等随机变量,以致采用蒙特卡洛技术求解时效率低下。本节运用“场景运算”方法对随机变量的不确定性进行处理,直接求取系统的运行风险指标。
4.1.1 多维风电出力的场景化
场景化可理解为用一组离散的概率分布序列[yi,Pr(i)](i=1,2,…,S)近似描述连续分布函数的过程。 其中,yi和 Pr(i)分别表示场景 i的分位点以及相应的概率,多维风电出力场景化的方法为[13,17]:
a.产生满足t-Copula分布的系列二维风速样本,并将样本分为S类,将各类中心(该类中所有样本的均值)ui=(ui1,ui2,…,uin)(i=1,2,…,S)作为场景的分位点;
b.统计每类中的样本数占样本总数的比例,将其作为各场景的概率值 P(i)(i=1,2,…,S);
c.采用式yi=Fi-1(ui)将各场景的分位点转换为原联合分布函数的场景,再计算出所需的风电场出力场景分位点,各分位点对应的概率为 P(i)(i=1,2,…,S)。
4.1.2 基于场景运算的系统风险评估
本文以“切负荷”风险约束为例,简述风险指标的计算过程。
a.进行风电出力场景化建模,并计算风电总出力的场景分位点
b.将系统负荷波动Δpload进行场景化建模,并利用全概率公式得到等效风电出力pe的场景概率序列[pe(i),Pr(i)](i=1,2,…,S)。
c.当pe以某一概率取值pe(i)时,系统所需的正旋转备用容量将以相同概率取值,因此,若其场景序列为[ru(i),Pr(i)],则场景分位点 ru(i)为:

d.若此时系统能提供的最大正旋转备用为Su,则系统“切负荷”风险水平为:

其中,rumax(i)和 rumin(i)分别为正旋转备用需求的最大和最小场景分位点;nmax为满足条件 Su<ru(i)的最大场景个数。
4.2 基于IQPSO算法的模型求解
4.2.1 QPSO算法基本原理
QPSO算法是在PSO算法粒子收敛行为的研究成果基础上,从量子力学的角度出发,对经典PSO算法进行简化后提出的一种新型PSO算法[18-20]。QPSO算法不仅能有效地应用于优化问题的求解,并且粒子状态只需通过位置向量描述,更加易于实现。
当粒子在搜索空间中移动时,存在着一个以局部吸引点为中心的delta势能吸引着粒子,这正是粒子能够保持聚集性的原因[18-19]。定义该局部吸引点为:

其中,pi,j(r)为第 r代第 i个体第 j维的局部吸引点;pbesti,j为个体最优值;gbest,j为全局最优值;u 为[0,1]之间的随机数。
粒子的位置更新方程为[20]:

其中,β 为控制参数;rand(0,1)表示一个[0,1]之间的随机数;mb,j(r)为第 r代第 j维的平均最优位置,即所有粒子自身最优位置的中心,如式(30)所示。

其中,ns为粒子群体大小。
4.2.2 IQPSO算法
(1)动态参数调整。
QPSO算法中,控制参数少,易于实现,但对该参数的控制和选择将直接影响到算法的收敛性。因此,本文采用动态控制策略调整β,使其值按余弦规律变化。这样可使得β既能在迭代初期较长时间保持较大值以保证算法的搜索效率,又能在迭代后期保持较小值以提高算法的搜索精度,即:

其中,r为当前迭代次数;rmax为允许迭代的最大次数;βmax和βmin分别为控制参数的初始值和最终值。
(2)精英学习模式。
为提高算法的全局寻优能力,本文建立了粒子早熟判断机制并在算法中引入精英学习模式。首先,为每个粒子设置一个停滞计数器,若粒子在迭代中停止更新,则计数器加1。当粒子停止更新的次数小于设定的阈值时,按QPSO算法寻优,否则认定其早熟并进入精英学习模式。在本文中,选取全局最优解的任意一维pd(根据机组出力费用灵敏度大小选取)作为扰动项,并在其附近搜索。精英学习模式通过Beta分布表示如下:

其中,min(Δ)为系统中所有常规机组的最小爬坡速率;Betarnd(α,λ)为均值和方差分别为 μ=α /(α+λ)、的随机Beta分布,本文设λ为1,类似于时变的神经网络策略,α也随着迭代次数线性变化,即:

其中,αmax、αmin分别为α的最大值和最小值。
将场景运算与IQPSO算法相结合,对含风电场的电力系统动态经济调度模型进行求解,算法流程图4所示。
5 算例结果与分析
本文对图5所示含2个邻近风电场的IEEE 30节点系统进行仿真计算,验证所提方法的可行性和有效性。假设风电场装机容量均为60 MW,风机的切入、额定和切出风速分别为4 m/s、14 m/s和30 m/s,σv=0.5。电能短缺和电能盈余等不确定成本系数分别为 k1=30$/(MW·h),k2=15$ /(MW·h)[16]。各节点负荷信息见文献[21],研究周期为3 h(每时段为1 h)。常规机组参数见表2,各时段的风速预测值如表3所示,风险阈值为0.05。αmax、αmin分别取1.0和 0.2,βmax=1.0、βmin=0.5[20]。为对比分析风电场的接入以及风速相关性对系统优化调度的重要影响,设计了如下3种运行方式,优化结果如表4所示。

图4 算法流程图Fig.4 Flowchart of algorithm

图5 IEEE 30节点系统拓扑结构Fig.5 Topology of IEEE 30-bus system

表2 常规机组部分参数Table 2 Parameters of conventional units

表3 风速和负荷预测结果Table 3 Forecasted wind speeds and loads

表4 不同运行方式下的优化结果对比Table 4 Comparison of optimization results among different operating modes $
方式1:不考虑风电功率并网。
方式2:考虑考虑风速t-Copula分布,但风电计划出力不参与优化,即以风电功率预测值作为计划出力值。
方式3:考虑考虑风速t-Copula分布且风电计划出力参与优化。
由表4可知:相比风电场并网前,方式2、3的系统不确定性成本均有不同程度的上升,然而系统的发电总成本却分别节省了10.4%和10.8%,这表明,风电场的“替代”效应,虽然牺牲了一定的系统可靠性,但能获取更大的经济利益;对比方式2和方式3可知,通过优化风电计划出力,降低了没有充分利用风电资源而造成的资源浪费,因此系统的总成本能够降低0.471%,为此带来相当可观经济效益。
表5给出了考虑风速t-Copula分布时的常规机组和风电场各时段的最优计划出力值,即方式3的动态经济调度方案,该最优解下各时段的风险指标如表6所示。由表5可知,各时段的风电最优计划出力均明显高于其预测值,因此,系统的“切负荷”风险也明显高于“弃风”风险。同时,由于风电场并网位置为节点10、20,与其相连接的线路有较大的功率传送能力,因而线路过载风险为0。若此时风电并网位置改为节点22、27,由于与其相邻的线路25-27承担风电功率的外送且传送容量较小,因而成为系统的最薄弱环节,此时线路过载风险达到4.9%,成为制约系统经济运行的主要因素,而系统的调度总成本也上升了2.65%,达到$2.7088×104。

表5 经济调度方案Table 5 Economic dispatch scheme

表6 系统优化结果Table 6 Result of system optimization
在前文的基础上,忽略风电场彼此之间的相关关系,即分别将2个风电场视为统一的整体以及假设两者相互独立,研究风电场相关性对调度结果的影响,结果如表7所示。由表7可知,随着风速间的相关性降低,调度成本呈下降趋势。其中与考虑风速的t-Copula分布的情形相比,风速相互独立时的调度成本下降$5.08×102。这是由于随着风速趋于独立时,系统中的风电总功率的波动范围将随之变小。这不仅使得系统潮流的波动范围及其对系统的扰动随之变小,而且系统约束条件满足的概率相对提高,风险指标下降,风电计划出力相对提高。因此系统确定性成本和不确定性成本都有所下降。由此可以预见,若风电场间的风速分布为负相关时,则各并网风电场出力趋于互补,电网运行成本将大幅下降。然而一般而言,邻近风电场的风速均为正相关,若忽略其相关关系,不仅会造成调度决策上的误差,而且以该调度方案运行势必会造成系统越限,危害系统运行安全。

表7 不同相关性下的调度结果Table 7 Dispatch results for different correlations $

表8 不同方法结果对比Table 8 Comparison of optimization results among different methods
针对第1时段优化结果,以本文所提方法的计算值和其他方法计算结果进行比较,从而验证场景运算处理机会约束的有效性以及IQPSO算法的优越性,结果如表8所示。由此表明本文所提IQPSO算法具有更强的全局寻优和局部求精能力。同时,由于算例中含多个随机变量,采用蒙特卡洛模拟时,为保证求解精度,须进行大量的随机抽样,因此运行速度较慢。在本算例中,采用场景运算对风险指标直接求解,可以全面考虑各随机变量的可能取值,准确直观地反映出系统运行中的风险水平,且大幅提高了模型求解速度。
此外,本文在不考虑常规机组成本的情况下,研究风电不确定成本与计划出力的关系,如图6所示。随着风电计划出力的增加,系统的不确定性成本呈现先降低后增高的趋势,各曲线对应的最低点即为各时段不确定性成本的最优值,对应的计划出力即为该时段最优风电计划出力。由图可知,各时段最优风电计划出力和不确定性成本均低于方式3的优化结果。可见,在所给定的电能短缺和盈余成本系数下,风电的“替代”效应所降低的火电机组燃料成本显然要比风电不确定性带来的成本更高。因此,在此条件下制定调度计划时,更希望让风电场多发电而不是让其的不确定性成本达到最低。

图6 风险成本与风电计划出力关系曲线Fig.6 Curve of risk cost vs.scheduled wind power output
在方式4的基础上,考虑风电系统的风险阈值对调度结果的影响,如图7所示。由图7可知,总成本与风险阈值成负相关,特别地,当时α=β=0,该模型变为确定性优化模型,系统调度成本为$2.6660×104,远高于 α=β=0.1时的$2.6378×104。 这是由于随着风险阈值的增大,系统可靠性要求降低,一方面允许更大的风电计划出力,另一方面允许某些概率很低但不满足约束条件的情况出现,降低了系统备用需求,提高了机组运行效率,因此运行成本有较大程度的下降。这也说明牺牲一定系统可靠性,能在一定程度上获得更大的经济利益。当其风险阈值超过0.063时,由于系统受到其他约束条件的限制,总成本基本趋于恒定,在此风险水平下时,牺牲系统可靠性对运行总成本的贡献被大幅削弱。因此可以认为该风险阈值即为系统最佳风险水平。可见,要保证系统绝对可靠地运行,且不允许任何浪费,电网投运成本非常高。因此,在实际电力系统中,只需将风险指标约束在可控的风险阈值范围之内。规划人员可根据实际情况,兼顾电网对经济性和可靠性的要求综合评估最佳风险阈值。

图7 总成本与置信水平关系曲线Fig.7 Curve of total cost vs.confidence level
6 结论
本文在利用Copula函数分析风电场群的风速时空分布特性的基础上构造了风电功率的场景空间。通过定义风险指标,并在目标函数中加入风电概率成本项,建立了不确定环境下含风电场群的电力系统经济调度模型,有效地解决了调度决策中经济性与安全性之间的博弈问题。该模型采用基于场景运算的IQPSO算法进行求解,不仅提高了求解速度,且直观地反映系统运行的风险程度。研究表明,风速的时空分布特性、网络结构以及系统风险阈值等因素对调度结果都有重要的影响。
参考文献:
[1]周玮,彭煜,孙辉,等.含风电场的电力系统动态经济调度[J].中国电机工程学报,2009,29(25):13-17.ZHOU Wei,PENG Yu,SUN Hui,et al.Dynamic economic dispatch in wind power integrated system[J].Proceedings of the CSEE,2009,29(25):13-17.
[2]陈海焱,陈金富,段献忠.含风电场电力系统经济调度的模糊建模及优化算法[J].电力系统自动化,2006,30(2):22-26.CHEN Haiyan,CHEN Jinfu,DUAN Xianzhong.Fuzzy modeling and optimization algorithm on dynamic economic dispatch in wind power integrated system[J].Automation of Electric Power Systems,2006,30(2):22-26.
[3]MIRANDA V,HANG P S.Economic dispatch model with fuzzy wind constraints and attitudes of dispatchers[J].IEEE Transactions on Power Systems,2005,20(4):2143-2145
[4]LIU Yujiao,JIANG Chuanwen,XUE Guiting,et al.Risk reserve constrained economic dispatch of wind power penetrated power system based on UPSMC and SAGA algorithms[J].Research Journal of Applied Sciences,Engineering and Technology,2013,5(3):1067-1074.
[5]刘德伟,郭剑波,黄越辉,等.基于风电功率概率预测和运行风险约束的含风电场电力系统动态经济调度[J].中国电机工程学报,2013,33(16):9-14.LIU Dewei,GUO Jianbo,HUANG Yuehui,et al.Dynamic economic dispatch of wind integrated power system based on wind power probabilistic forecasting and operation risk constraints[J].Proceedings of the CSEE,2013,33(16):9-14.
[6]周玮,孙辉,顾宏.计及风险备用约束的含风电场电力系统动态经济调度[J].中国电机工程学报,2012,32(1):47-55.ZHOU Wei,SUN Hui,GU Hong.Dynamic economic dispatch of wind integrated power systems based on risk reserve constraints[J].Proceedings of the CSEE,2012,32(1):47-55.
[7]ORTEGA-VAZQUEZ M A,KIRSCHEN D S.Estimating the spinning reserve requirements in systems with significant wind power generation penetration[J].IEEE Transactions on Power Systems,2009,24(1):114-124.
[8]HETZER J,YU D C,BHATTARAI K.An economic dispatch model incorporating wind power[J].IEEE Transactions on Energy Conversion,2008,23(2):603-611.
[9]LI X H,JIANG C W.Short-term operation model and risk managementforwind powerpenetrated system in electricity market[J].IEEE Transactions on Power Systems,2011,26(2):932-939.
[10]邓崴,李欣然,徐振华,等.考虑风速相关性的概率潮流计算及影响分析[J].电网技术,2012,36(4):45-50.DENG Wei,LI Xinran,XU Zhenhua,etal.Calculation of probabilistic load flow considering wind speed correlation [J].Power System Technology,2012,36(4):45-50.
[11]潘雄,周明,孔晓民,等.风速相关性对最优潮流的影响[J].电力系统自动化,2013,37(6):37-41.PAN Xiong,ZHOU Ming,KONG Xiaomin,et al.The influence on optimal power flow caused by wind speed correlation [J].Automation of Electric Power Systems,2013,37(6):37-41.
[12]曲正伟,王京波,王云静,等.考虑运行风险约束的风电场群准入容量分析[J].电网技术,2013,38(7):1861-1866.QU Zhengwei,WANG Jingbo,WANG Yunjing,et al.Analysis on acceptable capacity of wind farm group considering operation risk constraints[J].Power System Technology,2013,38(7):1861-1866.
[13]黎静华,文劲宇,程时杰,等.考虑风电场群出力Copula相关关系的场景生成方法[J].中国电机工程学报,2013,33(16):30-36.LI Jinghua,WEN Jinyu,CHENG Shijie,et al.A scene generation method considering Copula Correlation relationship of multiwind farms power[J].Proceedings of the CSEE,2013,33(16):30-36.
[14]韦艳华,张世英.Copula理论及其金融分析上的应用[M].北京:中国环境科学出版社,2008:10-23.
[15]SHI Libao,WANG Chen,YAO Liangzhong,et al.Optimal power flow solution incorporating wind power[J].IEEE Systems Journal,2012,6(2):233-241.
[16]董晓天,严正,冯冬涵,等.计及风电出力惩罚成本的电力系统经济调度[J].电网技术,2012,36(8):76-80.DONG Xiaotian,YAN Zheng,FENG Donghan,etal.Power system economicdispatch consideringpenalty costofwind farm output[J].Power System Technology,2012,36(8):76-80.
[17]黎静华,韦华,莫东.含风电场最优潮流的Wait-and-See模型与最优渐近场景分析[J].中国电机工程学报,2012,32(22):15-23.LI Jinghua,WEI Hua,MO Dong.Asymptotically optimal scenario analysis and Wait-and-See model for optimal power flow with wind power[J].Proceedings of the CSEE,2012,32(22):15-23.
[18]SUN J,FENG B,XU W B.Particle swarm optimization with particles having quantum behavior[C]//Proceedings of the 2004 IEEE Congress on Evolution Computation.Piscataway,NJ,USA:IEEE,2004:325-331.
[19]陈功贵,陈金富.含风电场电力系统环境经济动态调度建模与算法[J].中国电机工程学报,2013,33(10):27-35.CHEN Gonggui,CHEN Jinfu.Environmental economic dynamic dispatch modeling and method for power systems integrating wind farms[J].Proceedings of the CSEE,2013,33(10):27-35.
[20]康燕,孙俊,须文波.具有量子行为的粒子群优化算法的参数选择[J].计算机工程与应用,2007,43(23):40-42.KANG Yan,SUN Jun,XU Wenbo.Parameter selection of quantumbehaved particle swarm optimization[J].Computer Engineering and Applications,2007,43(23):40-42.
[21]雷亚洲,王伟胜,印永华.基于机会约束规划的风电穿透功率极限计算[J].中国电机工程学报,2002,22(5):32-34.LEIYazhou,WANG Weisheng,YIN Yonghua.Wind power penetration limitcalculation based on chance constrained programming[J].Proceedings of the CSEE,2002,22(5):32-34.
