考虑变流器暂态调控的双馈风电机组三相短路电流计算方法
2016-05-23丁秀香林湘宁黄天意王增平
马 静,丁秀香 ,林湘宁 ,黄天意 ,王增平
(1.华北电力大学 新能源电力系统国家重点实验室,北京 102206;2.华中科技大学 强电磁工程与新技术国家重点实验室,湖北 武汉 430074)
0 引言
双馈风力发电机DFIG(Doubly-Fed Induction Generator)是当前风电领域应用最普遍的风电机组,具有逆变器容量小、有功和无功功率独立解耦控制等优点[1]。但是,在外部电网发生故障情况下,DFIG产生的过电流、过电压将严重危害发电机和变流器的正常运行[2-3],研究DFIG的短路特性,对于建立相应的保护方案意义重大。
目前,电网严重短路导致转子保护投入时短路电流暂态特性的研究已有较多文献报道[4-9],但都不涉及变流器的暂态调控分析,研究结果不能全面反映DFIG的故障特性。在电网电压发生轻度跌落、不足以投入转子保护时,DFIG将经历电机的电磁暂态和变流器调控的耦合过程,导致其短路暂态特性更为复杂[3]。文献[3]推导了转子保护未动作时定转子短路电流表达式,但未考虑变流器输出对定转子电流的影响;文献[10-11]推导了仅考虑转子侧变流器调控因素的短路电流表达式,未考虑网侧变流器调控作用。
鉴于此,本文提出一种考虑双侧变流器暂态调控的DFIG定转子短路电流的计算方法。首先建立电网发生短路时的故障等值网络,考虑转子变流器控制因素,求取该网络下的定转子电流,基于此,通过数学解析方法推导能描述直流母线电压波动的暂态公式以及网侧变流器短路过程的暂态调控公式,据此剖析直流母线电压波动特性以及网侧变流器的暂态特性,并揭示定子短路电流二倍频谐波分量的产生机理,同时推导谐波分量的表达式,最后得到定转子短路全电流表达式。仿真结果验证了网侧变流器暂态调控理论和短路电流表达式的正确性。
1 DFIG系统数学模型
DFIG系统等效电路如图1所示,其中RSC和GSC分别表示转子侧变流器和网侧变流器,目前交-直-交变流器通常采用脉宽调制PWM(Pulse Width Modulation)控制方式提供励磁电源[12]。

图1 双馈风力发电系统等效电路图Fig.1 Equivalent circuit of DFIG-based wind-power system
DFIG系统在同步旋转坐标系下矢量数学模型表示为[13]:


其中,us、ur、is、ir、ψs、ψr分别为双馈发电机定子和转子电压、电流和磁链的空间矢量;ω1为同步角速度,ω=ω1-ωr为转差角速度,即同步角速度与转子角速度的差值;eg为电网电压,eg=us;ug、ig分别为网侧变流器电压和电流;Udc、Cdc分别为直流侧电压和直流侧电容;Pg、Pr分别为网侧变流器和转子侧变流器输入功率;Lm、Ls、Lr分别为等效的励磁电感、定子电感和转子电感,且 Ls=Lm+Lls、Lr=Lm+Llr,Lls、Llr分别为双馈电机定、转子漏感。
2 考虑变流器暂态调节的DFIG短路特性
2.1 考虑转子侧变流器控制的DFIG故障等值网络
电网发生故障时,建立考虑转子变流器暂态调控影响的故障等值网络,将其分解为正常运行网络和故障附加网络,如图2所示。故障附加网络不仅受定子侧附加电源控制,即Δus=-Aus0,其中A为机端电压跌落深度率,us0为稳态定子电压矢量;而且还受变流器调节的转子侧故障附加电源控制,忽略开关暂态,并设转子侧变流器电流回路闭环宽带足够大[14],变流器交流侧电压可无差跟踪参考值。则转子侧故障附加电源可以表示为:

其中,Δi*r为故障附加网络中转子电流参考值矢量;Δir为故障附加网络中转子电流增量;kp、ki分别为转子变流器电流内环PI控制器的比例和积分参数。
假设在t=t1时刻,电网发生对称短路,正常运行网络如图2(b)所示,该网络下的定转子电流可表示为:

其中,ψsm为定子磁链幅值;Ps.ref、Qs.ref分别为定子侧有功和无功功率的参考值,可直接设定。
故障附加网络如图2(c)所示,此网络下的数学模型可表示为:

其中,s为转差率。

图2 考虑转子侧变流器调节的三相短路故障等值网络Fig.2 Equivalent networks considering RSC adjustment for three-phase short circuit fault
由式(9),根据磁链守恒定律及故障附加网络下定子磁链初值为零的条件,可求得故障附加网络下的定子磁链为:
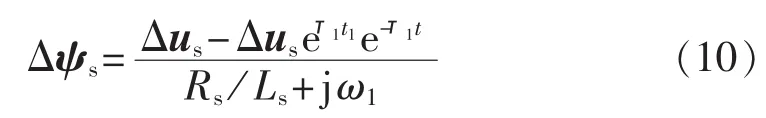
其中,τ1=Rs/Ls+jω1,为定子暂态磁链衰减常数。
将式(7)、式(10)代入式(9)的转子电压方程可得,故障附加网络下转子电流的二阶微分方程:

将式(9)中的定子磁链方程代入式(11),可得故障附加网络中定子电流的二阶微分方程:
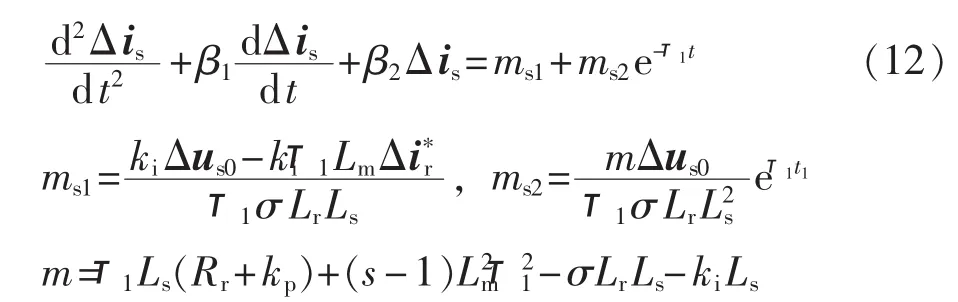
联立式(11)和式(12),可得故障附加网络下的定转子电流增量为:

式(13)与式(14)中,Δir0、Δis0分别为定转子电流强制分量,大小只与电机参数、机端电压跌落深度及短路发生时刻有关:

式(13)与式(14)中,Δirm、Δism分别为故障附加网络下的定转子暂态直流分量,其产生原因是定转子磁链不能突变,其大小还与转子侧变流器控制器参数密切相关:

式(13)与式(14)中,暂态自然电流分量 Δir1、Δis1分别为故障附加网络中,受定子磁链和转子变流器耦合控制作用下的电流增量,其衰减时间常数α1、α2受PI参数影响,其大小也与机端电压跌落深度及转子侧变流器控制器参数有关:

由式(8)、式(13)—(18)可知,考虑转子侧变流器暂态调节作用的故障等值网络中定转子短路电流表达式为:

由式(19)和式(20)可知,故障等值网络中定转子短路电流包含强制分量、暂态直流分量和暂态自然分量,其大小与电机参数、PI控制器参数有关。
由上述分析可知,电网发生短路时,机端电压瞬间跌落,导致DFIG电机电磁和转子变流器耦合调控,定转子电流瞬间增大,造成直流母线电压两侧功率交换不再平衡,直流母线电压发生波动,为了抑制其波动,网侧变流器将进行调控,而调控又将进一步影响定转子电流暂态特性,因此,研究直流母线电压波动特性是剖析网侧变流器暂态特性的前提和基础。
2.2 直流母线电压波动特性分析
考虑到DFIG转子变流器采用定子磁链定向矢量控制策略,有 usd=0、usq=Us,由式(1)和式(4)可得稳态运行的定转子磁链为:

其中,Us为电网电压幅值。
式(1)—(4)中,考虑到 Lls=Lm、Llr=Lm,转子电压和网侧电流可表示为:

图1中,忽略电抗器的损耗以及开关功率器件的损耗,则网侧变流器输入功率Pg表示为:

转子变流器输入功率Pr为:
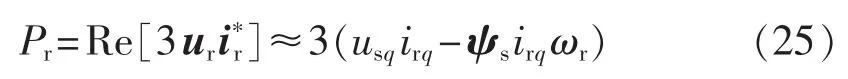
在网侧变流器中,直流母线电容储存电能为W=,其中Cdc为直流侧电容,由此可得直流母线电压平衡公式为:

由式(26)可知,DFIG稳定运行时,在网侧变流器的控制作用下,两侧变流器的功率交换为零,直流母线电压恒为定值。
当电网发生短路故障时,为便于分析直流母线电压波动特性,忽略机端电压相位跳变,同时,以超同步运行状态为例,故障后机端电压可表示为:

其中,k为电网发生短路故障后机端电压幅值跌落率,且k=1-A;Us0为稳态运行的机端电压幅值。
根据磁链守恒定律,由式(1)和式(27)可得短路后定子磁链为:
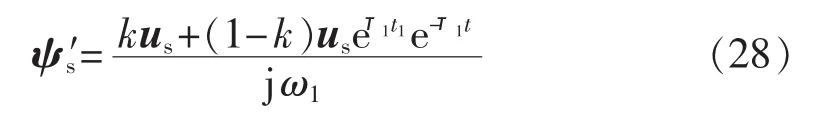
由式(22)、式(28)可得故障后转子电压为:

由式(24)、(25)与(28)可得故障后网侧变流器功率Pg和转子变流器功率Pr为:

根据式(26),可得直流侧的功率扰动为:

考虑到网侧变流器采用电网电压定向矢量控制策略,即将同步旋转dq坐标系d轴定向于电网电压矢量us的方向,则直流侧母线电压的静态增益可近似表示为[15]:

由式(32)和式(33),可得直流母线电压扰动为:

由式(32)和式(34)可知,直流侧扰动大小不仅与机端电压跌落程度、电机转速有关,还与转子短路电流密切相关,且机端电压跌落越深,直流母线电压波动越大。因此,为了稳定直流母线电压的波动,网侧变流器将进行调控,使直流母线电压差逐步降低,并最终保持在参考值附近。
2.3 网侧变流器短路控制过程分析
图3是网侧变流器控制模型,其通过引入电网电压前馈与反馈控制相结合,达到网侧d、q轴电流的独立控制,实现交流侧单位功率因数控制和直流母线电压稳定控制[16]。

图3 网侧变流器控制模型Fig.3 Control model of GSC
根据式(19),转子q轴电流分量可表示为:
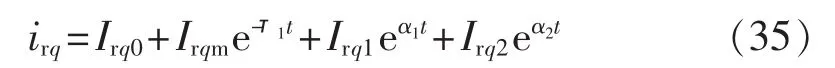
由式(34)、(35)可得,短路后直流母线电压为:

短路后,网侧变流器输入无功功率可表示为:
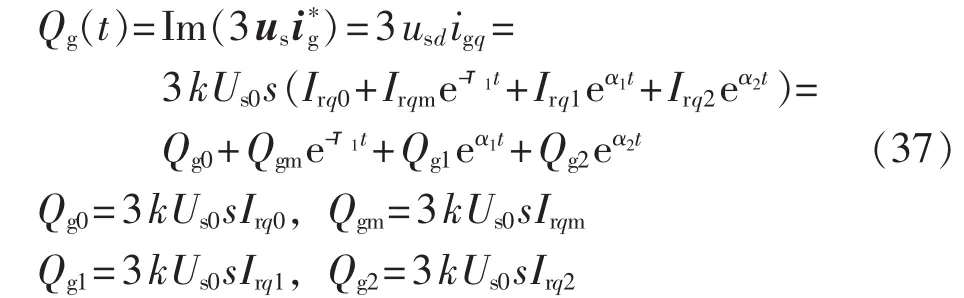
对式(36)和式(37)采用 Laplace 变换,可得其对应的拉氏方程为:

由图3外环PI控制器传递函数和式(38),可得网侧电流参考值的d、q轴分量拉氏方程为:

其中,Kp1、Ki1和 Kp2、Ki2分别为网侧变流器电压外环和功率外环的PI参数。
对式(39)进行Laplace逆变换,得到网侧电流参考值d、q轴时域表达式:

对式(40)进行Laplace变换后,代入图3中的电流环,经PI控制器计算得到网侧变流器电压参考值d、q轴分量解析式:

其中,Kp3、Ki3和 Kp4、Ki4分别为网侧变流器 d轴和 q轴电流环PI控制器参数。
对式(41)进行Laplace逆变换,可得网侧变流器电压参考值的时域表达式为:


由式(42)可以看出:电网发生对称短路时,网侧变流器控制器环节输出的参考电压d、q轴分量包含以τ1时间常数衰减且仅受网侧变流器影响的直流分量,以及受网侧变流器和转子侧变流器共同影响的暂态直流分量和暂态自然分量;每个分量的幅值与变流器PI参数、短路发生时刻、衰减时间常数、直流母线电压振荡幅值以及网侧变流器功率振荡幅值有关。
2.4 定转子短路电流解析式推导
式(40)与式(42)均在同步旋转坐标系下求取,将其归算至三相静止坐标系,可得网侧变流器电压和电流参考值中主要包含基频分量和二倍频分量。
根据PWM原理[17],网侧变流器的二倍频电流分量,经过双PWM将在转子侧产生相对于定子的2 f1谐波电流分量,此电流产生的旋转磁场相对于转子绕组本身角速度是 2ω1-ωr=(1+s)ω1,且该电流可表示为:

其中,Uge(2f1)为网侧变流器交流侧调制信号中频率为2f1的电压分量;Utri为载波信号幅值。
对于(1+s)f1电流分量,由于电机内部绕组的耦合作用,定子绕组将感应出2ω1频率的短路电流。假定电网电压仅含基波分量,则电网侧近似短路[18],将定子绕组参数归算到转子绕组后,转子(1+s)f1电流分量等效电路如图4所示。

图4 转子(1+s)f1电流分量等效电路Fig.4 Equivalent circuit of rotor(1+s)f1current
由图4可知,定子短路电流二倍频的谐波电流分量为:

其中,ssr为转子(1+s)f1电流分量等效电路的等效转差;X′s(1+s)为归算至转子绕组的等效定子漏感;Xm(1+s)为等效互感。
定子短路电流二倍频分量产生的机理是电网发生短路时,由于定子磁链和转子变流器的控制作用,定转子绕组分别产生含有强制分量、暂态直流分量和暂态自然分量的电流,导致直流母线电压和网侧无功功率发生振荡,引起网侧变流器进行综合调控,网侧变流器电压和电流都将产生二倍频分量,经过双PWM,在转子绕组产生(1+s)f1的谐波电流分量,最后在定子绕组感应出二倍频的谐波电流分量。因此,电网发生三相短路故障时的定、转子短路全电流为:
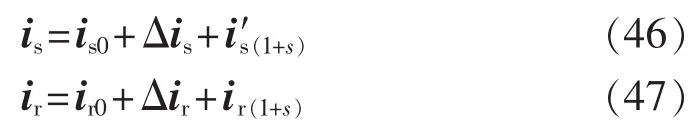
其中,is0、ir0为正常网络下的电流增量;Δis、Δir为故障附加网络下的电流增量;i′s(1+s)、ir(1+s)为综合双侧变流器暂态调控下的电流谐波增量。
3 仿真验证
3.1 仿真系统简介
为了验证本文所推导的短路电流表达式和短路过程变流器调控理论的正确性,以全面分析DFIG的短路电流暂态特性,在PSCAD/EMTDC软件搭建了2 MW DFIG单机无穷大系统仿真模型。实验系统如图5所示,风机主要参数为:额定功率2 MW,定子额定电压690 V,额定频率50 Hz,定子电阻0.0054 p.u.,转子电阻0.00607 p.u.,定子漏感0.102 p.u.,转子漏感0.11 p.u.,互感为4.362 p.u.。双侧变流器参数见表1。
3.2 短路电流验证
假设在t=2s时刻,变压器高压侧发生三相对称短路故障,DFIG机端电压跌落约至60%,由式(46)和式(47)求得定转子三相电流(标幺值),以a相为例,如图6所示。
由图6可知,定转子短路电流计算值与仿真值的大小和变化趋势吻合,且暂态衰减明显,符合故障时刻以及故障过程中定转子短路电流暂态特性。特别是第一周期基本吻合,但在200 ms之后转子电流计算波形逐步滞后于仿真波形,这是因为计算中未计及转速变化,即计算结果的频率保持不变,但DFIG实际运行中为了保持电网频率不变,转子电流频率增加。考虑到电网短路持续时间较短,可以忽略稳态转速带来的误差。

图5 仿真系统图Fig.5 Simulation system
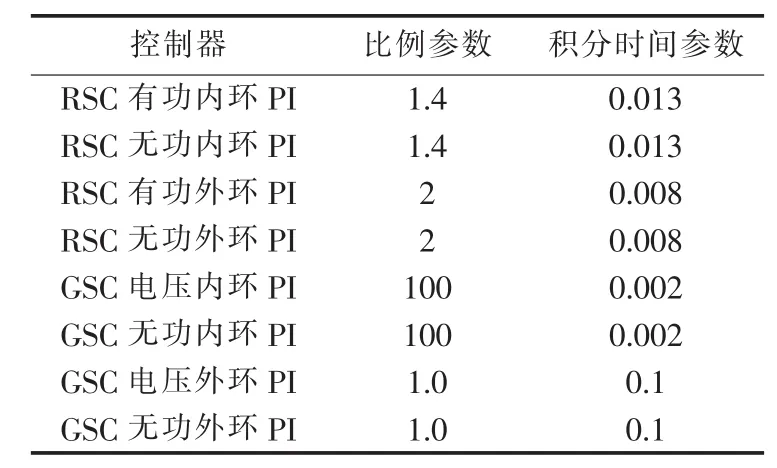
表1 转子侧变流器和网侧变流器参数Table 1 Parameters of RSC and GSC

图6 考虑变流器暂态调节的定、转子短路电流Fig.6 Stator and rotor short circuit currents considering converter adjustment
3.3 直流母线电压波动特性验证
图7是直流电容侧功率差和直流母线电压偏差(均为标幺值)对比曲线。由图7可以看出:电网发生三相对称短路时,直流电容侧功率差和直流母线电压偏差变化基本一致,说明短路时正是因为电容两侧功率差不再为零,导致电容电压发生较大波动,在网侧变流器容量足够大情况下,它的调控作用将使直流母线电压偏差和功率差逐步降低,并最终稳定至参考值附近。图8为不同机端电压跌落下的直流母线电压偏差(标幺值)曲线。由图8可知,电网故障越严重,即机端电压跌落越深,直流电压偏差最大值越大,波动也越大。
3.4 定子短路电流二倍频谐波分量验证
为了验证定子短路电流存在二倍频谐波分量,通过采用改进的全波傅里叶算法提取短路电流中的二倍频谐波[19],如图9所示。图9中,机端电压跌落率约0.5时,定子短路电流仿真值A、B、C相谐波含量分别约为16.12%、12.36%和14.96%,网侧短路电流仿真值A、B、C相谐波含量分别为12.70%、8.74%和7.03%,说明电网发生短路时,在双侧变流器的综合调控作用下,定子电流和网侧电流都产生二倍频谐波电流分量,使短路电流特性更为复杂。

图7 电网短路下直流母线功率差和电压偏差对比曲线Fig.7 Comparison between power deviation and voltage deviation of DC bus during grid short circuit

图8 不同机端电压跌落下的直流母线电压偏差曲线Fig.8 Curve of DC bus voltage deviation for different terminal voltage drops

图9 短路电流二倍频谐波含量Fig.9 Percentages of double-frequency harmonic in stator short circuit current

表2 不同电压跌落情况下的定子短路电流二倍频谐波含量百分比Table 2 Percentage of double-frequency harmonic in stator short circuit current for different terminal voltage drops
表2和表3分别是不同机端电压跌落程度下的定子短路电流和网侧短路电流的二倍频谐波含量(机端电压为标幺值)。从表2中可知:机端电压跌落10%时,A相谐波含量为12.80%,B相谐波含量为9.21%,C相谐波含量为10.80%;机端电压跌落50%时,A相谐波含量高达16.12%,B、C相也分别含有12.36%和14.96%的谐波分量。从表3也能得出类似结论。表2和表3的仿真结果均表明:机端电压跌落越严重,短路电流的二倍频谐波含量也越多,并已出现超过变压器二次谐波制动整定值(15%)的情况[20],有可能引起二次谐波制动元件误动作。

表3 不同电压跌落情况下的网侧短路电流二倍频谐波含量百分比Table 3 Percentage of double-frequency harmonic in grid-side short circuit current for different terminal voltage drops
4 结论
电网发生对称短路时,将引起DFIG与变流器的耦合控制,导致DFIG定转子电流的暂态特性变得十分复杂。本文提出综合考虑双侧变流器暂态调节的DFIG短路电流计算方法,特点如下:
a.建立考虑转子变流器控制的故障等值网络,推导该网络下的定转子电流,并指出每个分量的产生原因和影响因素;
b.计及直流母线电压波动情况,推导了网侧变流器双环暂态调控公式,揭示了网侧变流器暂态特性机理,探讨了双侧变流器综合调控是短路电流二倍频谐波分量产生的原因,并进一步推导了谐波分量的表达式;
c.仿真实验结果验证了本文所推导公式及相关理论的正确性,该结果有利于掌握DFIG与变流器暂态过程的耦合机制,对于计算故障电气量具有重要意义。
参考文献:
[1]龚文明,胡书举,许洪华,等.一种适用于大型风电场实时仿真的双馈风力发电机响应模型[J].电力自动化设备,2014,34(4):114-119.GONG Wenming,HU Shuju,XU Honghua,et al.Response model of DFIG for real-time simulation of large-scale wind farms[J].Electric Power Automation Equipment,2014,34(4):114-119.
[2]RAHIMI M,PARNIANI M.Grid-fault ride through analysis and control methods for wind turbines using doubly-fed induction machines[J].Electric Power Systems Research,2010(8):184-195.
[3]欧阳金鑫,熊小伏,张涵轶.并网双馈风电机组在电网短路时的特性研究[J].中国电机工程学报,2011,31(22):17-25.OUYANG Jinxin,XIONG Xiaofu,ZHANG Hanyi.Characteristics of DFIG-based wind generation under grid short circuit[J].Proceedings of the CSEE,2011,31(22):17-25.
[4]MORREZ J,HSSN S W H.Short-circuit current of wind turbines with doubly fed induction generator[J].IEEE Transactions on Energy Conversion,2007,22(1):174-180.
[5]周宏林,杨耕.不同电压跌落深度下基于撬棒保护的双馈式风机短路电流特性研究[J].中国电机工程学报,2009,29(增刊 1):184-191.ZHOU Honglin,YANG Geng.Short circuit current characteristics of doubly fed induction generator with crowbar protection under different voltage dips[J].Proceedings of the CSEE,29(Supplement 1):184-191.
[6]张建华,陈星莺,刘皓明,等.双馈风力发电机三相短路分析及短路器最大电阻整定[J].电力自动化设备,2009,29(4):6-10.ZHANG Jianhua,CHEN Xingying,LIU Haoming,etal.Threephase short-circuit analysis for doubly fed wind-driven generator and short-circutiter maximal resistance calculation[J].Electric Power Automation Equipment,2009,29(4):6-10.
[7]徐殿国,王伟,陈宁.基于撬棒保护的双馈电机风电场低电压穿越动态特性分析[J].中国电机工程学报,2010,30(22):29-36.XU Dianguo,WANG Wei,CHEN Ning.Dynamic characteristic analysisofdoubly-fed induction generatorlow voltage ridethrough based on crowbarprotection [J].Proceedingsofthe CSEE,2010,30(22):29-36.
[8]朱晓东,石磊,陈宁,等.考虑Crowbar阻值和退出时间的双馈风电机组低电压穿越[J].电力系统自动化,2010,34(18):84-89.ZHU Xiaodong,SHI Lei,CHEN Ning,et al.An analysis on low voltage ride through of wind turbine driven doubly fed induction generator with different resistances and quitting time of Crowbar[J].Automation of Electric Power Systems,2010,34(18):84-89.
[9]郑重,杨耕,耿华.电网故障下基于撬棒保护的双馈风电机组短路电流分析[J].电力自动化设备,2012,32(11):7-14.ZHENG Zhong,YANG Geng,GENG Hua.Short-circuit current analysis for DFIG-based wind generation system with crowbar protection under grid faults[J].Electric Power Automation Equipment,2012,32(11):7-14.
[10]熊小伏,欧阳金鑫.电网短路时双馈感应发电机转子电流的分析与计算[J].中国电机工程学报,2012,32(28):115-121.XIONG Xiaofu,OUYANG Jinxin.Analysis and calculation of rotor currents for doubly-fed induction generators under short circuits in power grids[J].Proceedings of the CSEE,2012,32(28):115-121.
[11]OUYANG Jinxin,XIONG Xiaofu.Research on short-circuit current of doubly fed induction generator under non-deep voltage drop[J].Electric Power Systems Research,2014,107:158-166.
[12]李晶,宋家骅,王伟胜.考虑变频器特性的变速恒频双馈风力发电机组控制策略的研究与仿真[J].电网技术,2004,28(21):11-16.LI Jing,SONG Jiahua,WANG Weisheng.Study and dynamic simulation of control strategy for variable speed wind turbine with double-fed generator considering frequency converter characteristics[J].Power System Technology,2004,28(21):11-16.
[13]张艳霞,童锐,赵杰,等.双馈风电机组暂态特性及低电压穿越方案[J].电力系统自动化,2013,37(6):7-12.ZHANG Yanxia,TONG Rui,ZHAO Jie,et al.Transient characteristics analysis and low voltage ride-through scheme of doublyfed wind turbine generators[J].Automation of Electric Power Systems,2013,37(6):7-12.
[14]HARNEFORS L,NEE H P.Model-based current control of AC machines using the internal model control method[J].IEEE Transactions on Industry Applications,1998,34(1):133-141.
[15]郭家虎,张鲁华,蔡旭.双馈风力发电系统在电网三相短路故障下的响应与保护[J].电力系统保护与控制,2010,38(6):40-44.GUO Jiahu,ZHANG Luhua,CAI Xu.Response and protection of DFIG system under three-phase short circuit fault of grid[J].Power System Protection and Control,2010,38(6):40-44.
[16]邹高域,赵争鸣,袁立强,等.双PWM变换器的系统安全工作区及其应用[J].电力自动化设备,2014,34(3):82-88.ZOU Gaoyu,ZHAO Zhengming,YUAN Liqiang,et al.Systematic safe operating area of dual-PWM converter and its application[J].Electric Power Automation Equipment,2014,34(3):82-88.
[17]HU Lihua,ROBER Y.Harmonic transfer through converters and HVDC links[J].IEEE Transactions on Power Electronics,1992,7(3):514-525.
[18]熊小伏,齐晓光,欧阳金鑫.双馈风电机组短路电流对变压器保护二次谐波制动的影响[J].中国电机工程学报,2014,34(13):2201-2209.XIONG Xiaofu,QI Xiaoguang,OUYANG Jinxin.Effect of doublyfed wind turbinesshort-circuitcurrenton second harmonic escapement of transformer protection [J].Proceedingsofthe CSEE,2014,34(13):2201-2209.
[19]苏文辉,李钢.一种能滤去衰减直流分量的改进全波傅氏算法[J].电力系统自动化,2002,26(23):42-44.SU Wenhui,LI Gang.An improved full-wave Fourier algorithm for filtrating decaying DC component[J].Automation of Electric Power Systems,2002,26(23):42-44.
[20]张保会,尹项根.电力系统继电保护[M].2版.北京:中国电力出版社,2009:181.
