基于风险评估和机会约束的不确定性可中断负荷优化调度
2016-05-23牛文娟
牛文娟,李 扬,王 磊
(东南大学 电气工程学院,江苏 南京 210096)
0 引言
需求响应[1]DR(Demand Response)项目中的可中断负荷IL(Interruptible Load)项目在国外电力市场中已得到了广泛的应用,一些国家和地区先后引入了IL措施。它通过与用户签订合同来确定IL,灵活性较强,能有效控制峰谷差,提高社会资源利用率。随着需求侧的逐步放开,IL作为一种虚拟的备用发电容量资源和输电容量资源,在调峰、降低阻塞和新能源消纳等方面越来越受到关注[2-4]。我国经济发展迅速而出现的电力供应紧张局面、人们环保节能意识的增强以及IL自身所具有的优势,使得IL项目的开展具有迫切性和可行性。
复杂系统的处理往往难以回避定性的、不精确的、不完全的和不确定的信息[5]。在实施IL项目时,从获取数据、下发命令、用户执行等各个环节均存在不确定性。文献[6]考虑各不确定性影响因素建立了IL风险收益评估模型。文献[7-9]在IL优化决策过程中分别考虑了现货价格的不确定性、发生意外事故的不确定性对备用水平的影响,以及多种能源需求的不确定性。但IL优化决策中的成本模型基本都是采用确定性成本模型,文献[10-12]以合同中约定的补偿价格来确定IL成本,文献[3,7,13-14]根据激励相容原理使用户上报用户类型参数,从而建立二次模型来确定IL成本。但由于没有考虑IL不确定性的影响,无法反映IL的实际成本,在调用IL资源时难免有一定的盲目性,因此必须要考虑IL的不确定性[15]。
文献[16]中已建立了初步的IL成本模型,考虑了IL削减量不确定造成的补偿费用成本不确定性,但该模型中不确定性越大,成本越低,导致削减不可靠的用户会被优先调用以降低成本,在优化模型中将方差作为优化目标的一部分,物理意义不清晰,且未考虑发电机与IL共同参与的调度流程。本文在已有研究成果的基础上对IL项目中的不确定性进行分析梳理,阐述了各种不确定性因素的分类和影响,提出了有IL参与的日前优化调度流程,对IL响应不确定性和削减需求不确定性进行描述,建立IL成本和风险的期望值模型。该不确定性模型能更为合理地反映电力公司在负荷高峰期调用IL的真实成本。
1 考虑响应不确定性的IL成本
1.1 IL不确定性分析
在电力市场过渡期的IL管理主要通过合同进行。多时间尺度的IL调度可作为电力系统调度的补充[17]。IL的不确定性主要来源于用户基线负荷、用户的响应行为、IL削减需求等多个因素。用户基线负荷预测类似于短期负荷预测,针对单个用户负荷进行预测,不确定性问题更为突出。当系统调度员向用户发出中断命令时,用户应自觉地做出响应进行负荷削减。合同中补偿价格的设置是以经济手段激励用户履行合同积极响应,惩罚价格的设置是以经济手段提高合同约束力,降低用户违约概率。但用户的实际响应情况受用户对响应效益的理性判断、次日突发状况和用户响应信誉的影响,使得用户的响应行为具有不确定性。IL削减需求取决于负荷预测、传统机组出力、新能源发电预测、线路阻塞情况、元件故障情况、备用水平等因素,由于这些因素的不确定性,IL削减需求存在不确定性。
1.2 IL支付成本
对签订了IL合同的用户下发负荷削减命令后,应定期进行费用结算,合理的补偿和惩罚可以刺激消费者积极可靠地参与IL项目。但用户响应情况存在不确定性,用户有可能欠响应或过响应,即用户实际负荷削减量有可能比要求的少或者多,因此用户得到的费用结算也存在不确定性。本文在文献[18]的基础上提出一种考虑用户响应不确定性,同时计及补偿成本和惩罚成本的IL用户费用结算方法。本文所提及的时段长度均为1 h。由于用户响应不确定性,实际削减负荷与要求削减负荷之差ξ是随机量,采用充足的历史数据可对用户实际负荷的预测误差进行估计,一般认为其服从正态分布[19-20]。可以得到用户i在时段t的总收入为:
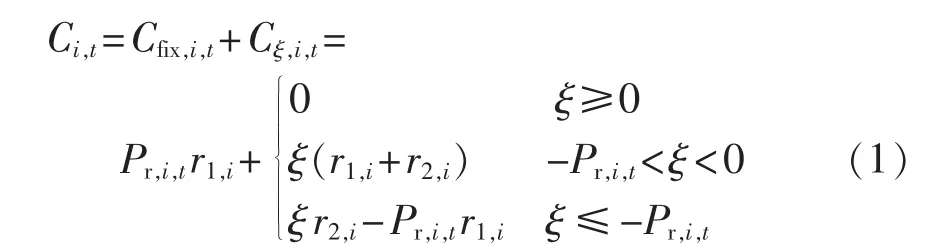
其中,Pr,i,t为用户 i在时段 t被要求削减的容量;r1,i和r2,i分别为 IL合同中约定的补偿单价和惩罚单价。
1.3 IL风险成本
根据风险理论,风险费用评估是一种将风险和经济因素放在同一价值尺度上来衡量的方法[21]。风险损失费用可用单位停电费用损失r乘以期望缺供电量计算。当用户欠响应时,电力公司需要承担重新购买高价备用容量和维护网络安全稳定性等风险,假设单位停电损失ro已知。当用户过响应时,电力公司需要承担售电量减小的风险,此时的损失价格为售电价格rp。对于电力公司而言,用户i每小时风险成本为:
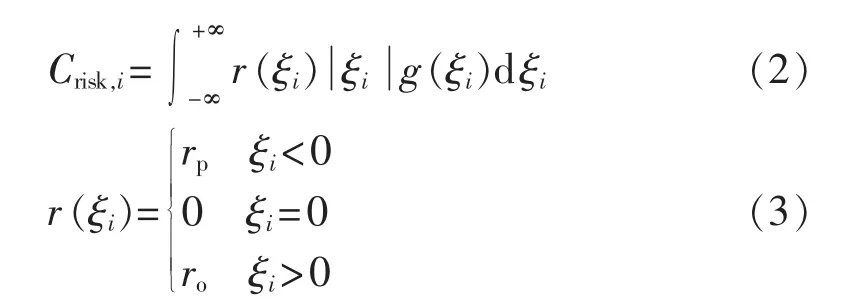
其中,ξi为第i个用户实际削减负荷与要求削减负荷之差;假设电力公司可根据历史统计数据得到用户响应情况的概率分布,g(ξi)为 ξi的概率密度函数。
2 削减总需求不确定性
在负荷高峰期由于负荷水平很高,供电能力和机组爬坡能力有限,往往会形成容量缺额。新能源发电的参与,使得备用水平提高,加剧了容量缺额紧张。本文假设IL的优化决策在同时间尺度调度系统之后,由IL来满足系统容量缺额。
2.1 容量缺额的不确定性描述
容量缺额主要源于两方面:一是系统供电不足,二是机组爬坡能力不足。
(1)系统供电不足导致的容量缺额。
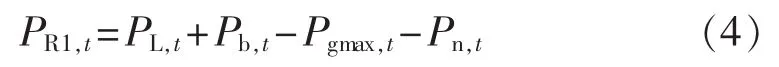
其中,PL,t为时段 t的预测负荷;Pb,t为时段 t的备用容量;Pgmax,t为时段 t可开机机组最大总出力;Pn,t为新能源发电时段t预测出力。
由于负荷预测和新能源的不确定性等,容量缺额呈现一定的不确定性,可用均值和随机偏差来表示:
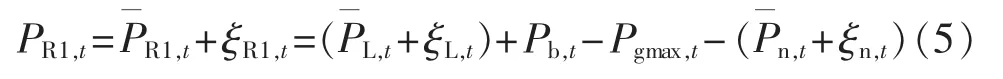
其中,分别为时段 t的削减需求、负荷预测期望值和新能源出力的均值;ξR1,t、ξL,t和 ξn,t为随机偏差,ξR1,t的概率密度函数为 ξL,t和 ξn,t的概率密度函数的卷积,假设 ξL,t和 ξn,t都服从正态分布,均值都为 0,方差分别是 σL,t和 σn,t,根据独立正态分布随机变量的特性,ξR1,t也服从正态分布,均值为 0,方差 σR,t= σL,t+ σn,t。
(2)机组爬坡能力不足导致的容量缺额。

其中,Pramp,t为所有机组从时段t-1到时段t的爬坡能力之和。
考虑负荷预测的不确定性,机组爬坡能力不足导致的容量缺额也可表示为的形式。
2.2 削减总需求的机会约束建模
在IL优化决策中,若要调用IL资源来完全满足削减需求,代价会非常高,比较合理的选择是满足削减需求的概率达到一个可接受的值。本文采取机会约束规划来描述削减需求的不确定性,机会约束规划中,允许决策在一定程度上不满足约束,但该决策使约束成立的概率不小于某一置信水平α[5]。因此削减需求与IL用户削减总量的关系如下:
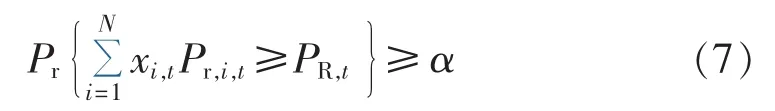
其中,N 为 IL 用户总数;Pr{·}为事件发生的概率;PR,t为容量缺额,PR,t=max(PR1,t,PR2,t);xi,t表示 IL 是否中断,是本文模型中的控制变量,xi,t=1表示用户i在时段t中断负荷,xi,t=0则表示用户正常用电。
可见,置信水平 α 越高,ξR,t的方差越大,需要调用的IL就越多。因此选择合适的置信水平,并提高负荷预测和新能源出力预测的精度是提高IL项目经济性的重要手段。
3 IL调度优化决策模型
根据提前通知时间和用户特性的不同,IL可参与日前计划、滚动计划和实时调度等多种时间尺度的系统调度。上文提出的考虑响应不确定性的IL成本建模方法,可适用于多时间尺度的优化决策。本文侧重于研究IL参与日前调度的优化决策,日前调度有充足的时间进行动态优化计算,一般是以安全为约束,以经济为目标。应充分利用IL,与高峰期调度结合,缓解容量缺额降低备用压力,提高系统可靠性。
3.1 IL参与日前调度的方式
根据2.1节所描述的容量缺额特点,给出IL参与日前调度的方式如图1所示。
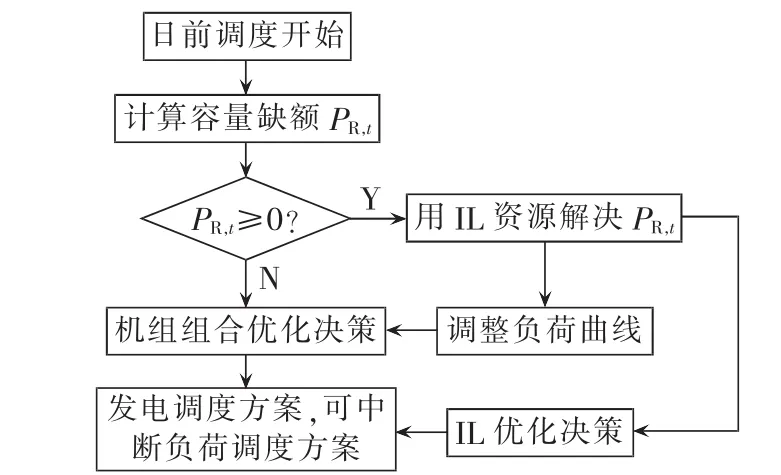
图1 IL参与日前调度流程图Fig.1 Flowchart of day-ahead dispatch including ILs
3.2 优化决策模型的目标函数和约束条件
本文在IL优化决策模型中考虑用户响应的不确定性和负荷削减需求的不确定性,建立单目标期望值模型,以调用IL总成本的期望值最小为优化目标。目标函数如下:
其中,T为IL事件总时长。
由该模型结构特点和期望值算子基本性质可得:
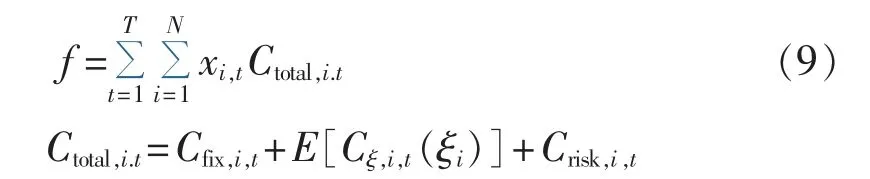
由此可见,在进行优化计算之前,可先计算出电力公司在时段t调用用户i的IL成本期望值Ctotal,i.t,以此避免采用蒙特卡洛法带来的庞大计算量。
为了与传统方法对比,在算例中也对固定补偿成本目标函数f1进行了优化计算。
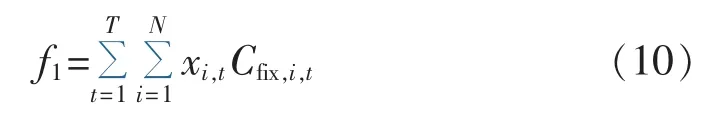
由于不同的电力企业对风险的考虑侧重程度不同,可为优化目标设定风险系数。通过调节风险系数大小来选择对风险不确定性的侧重程度,如下:
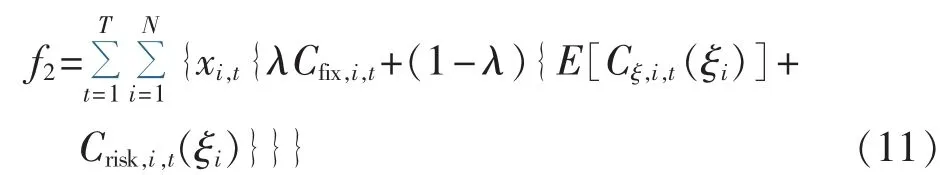
其中,λ为风险系数,λ<0.5为风险回避者,偏好于低风险的用户,λ>0.5为风险偏好者,偏好于风险大的用户,λ=0.5为风险中立者,希望预期成本最小化。
该目标函数须满足如下约束条件。
a.削减量约束条件见式(7),可将该问题转化为其等价类进行求解[5]。
b.削减间隔时间约束条件:
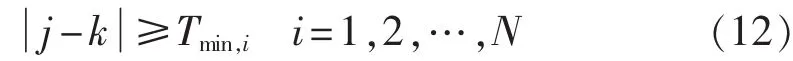
其中,时段j开始中断负荷;时段k恢复用电;Tmin,i为用户i 2次负荷削减事件间隔时间的最小值。
c.削减持续时间约束条件:
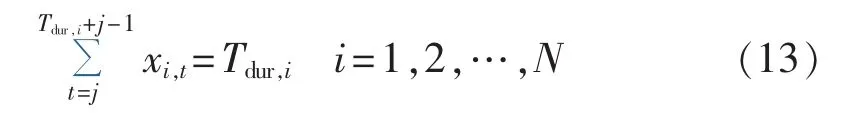
其中,时段 j开始中断负荷;Tdur,i为用户i的负荷削减持续时间。
d.削减总次数约束条件:

其中,NT,i为用户i在T时段内中断最大次数。
由此可见,本文所提出的基于风险评估和机会约束的不确定性IL优化决策模型,通过优化目标期望化和约束条件等价化处理后,是一个整数规划模型。
4 算例及分析
4.1 算例数据介绍
为了验证本文提出的IL参与日前调度的流程以及不确定性IL优化决策模型的有效性,算例采用广西某市的负荷数据和IEEE 30节点系统的发电机数据,并以该市若干工业负荷数据为基础进行计算。IL可视为多个用户的集合,根据中心极限定理,负荷削减量可近似视为服从正态分布[22]。假设实际削减负荷与要求削减负荷之差ξ呈均值为0的正态分布。用ξ的标准差 σ占要求削减负荷量Pr,i的比例来表示用户的响应可靠程度,即σ/Pr,i越小表示用户响应越可靠。
(1)第1组。不同行业的企业由于电价在成本效益中所占比例不同,当用户的补偿价格和惩罚价格越高时,一般情况下用户响应可靠性越高。60个用户来自3个行业,数据在表1的基础数据上变化得到。

表1 3个行业的用户基础数据Table 1 Basic customer data of three industries
(2)第2组。60个用户分为3个小组,每一小组都固定2个参数不变,第3个参数变化,如表2所示。
假设电力公司缺电成本为10元/(kW·h),电价为1元/(kW·h)。在MATLAB中采用YALMIP建模工具箱进行建模,调用CPLEX求解。

表2 3个用户组的IL参数Table 2 IL parameters of three customer groups
4.2 IL参与日前调度
根据3.1节的流程图进行日前调度计算,得到各个时段的负荷削减量如表3所示。假设每个时段的负荷削减需求均呈正态分布,方差为均值的1%,置信水平为0.9。采用第1组用户参与IL优化决策,机组组合和IL调度结果如图2所示。
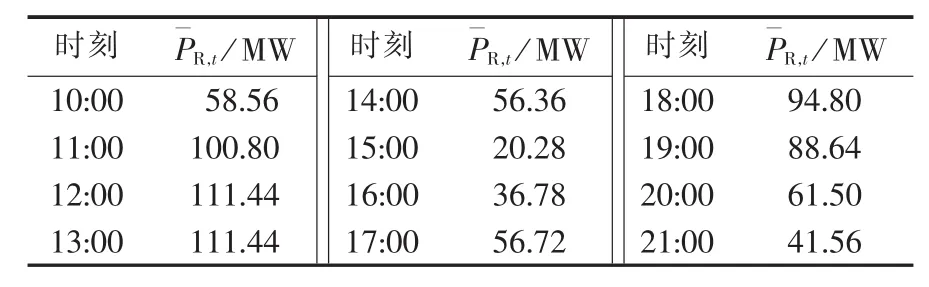
表3 各个时段的负荷削减量Table 3 Load curtailment for different periods
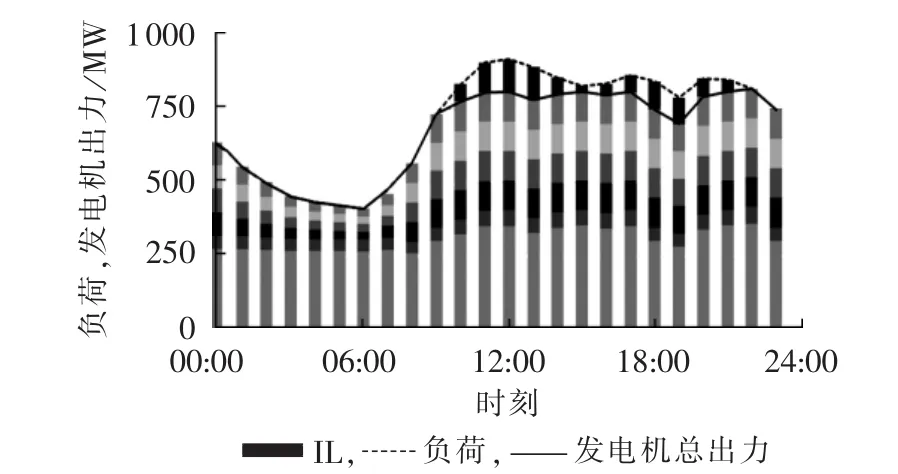
图2 IL参与的机组组合结果Fig.2 Results of UC considering ILs
4.3 确定性和不确定性IL优化决策对比
采用第1组用户参与优化决策,并设置3种优化场景如表4所示。

表4 优化场景定义Table 4 Definition of optimized scenarios
计算电力公司在整个优化时段f、f1和对IL的实际支付成本期望值以对比分析不同优化场景对各成本的影响,见表5。场景3优化结果只能保证50%的概率满足削减总需求。由于总需求要求低,因此所调用的用户较少,导致场景3成本最低,但也会导致电力公司不能达到削减负荷要求,额外削减负荷的风险增大。
为了与补偿价格对比,将用户的总成本期望值除以IL容量得到用户的综合价格。图3和图4分别为IL用户调用情况与补偿价格和综合价格的关系,阴影表示该用户被调用。场景2、3优先调用补偿价格较低的用户,但总成本期望值较高。场景1能够调用一些虽然补偿价格较高但综合价格较低的用户,合理反映IL成本。
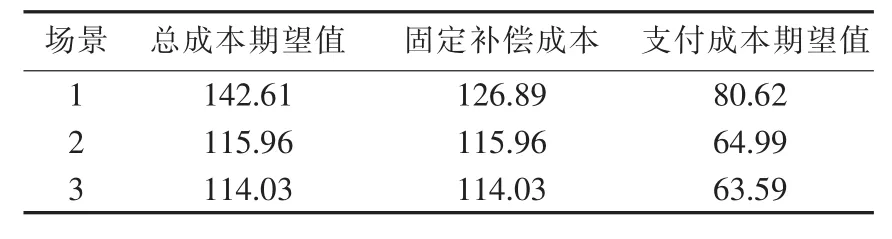
表5 3种场景下的成本Table 5 Costs of three scenarios 万元

图3 IL用户调用情况(用户按照补偿价格排序)Fig.3 IL dispatch(sorted by compensation price)
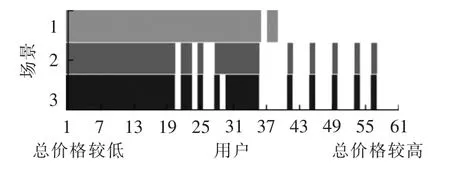
图4 IL用户调用情况(用户按照综合价格排序)Fig.4 IL dispatch(sorted by total price)
确定性模型无法考虑用户响应不确定性对成本的影响,削减需求估计较为保守,使得负荷削减较少,但增加了额外削减负荷的风险。而本文提出的不确定性模型则在考虑用户响应不确定性的基础上更为合理地反映IL成本,能考虑削减需求的满足概率。
4.4 用户IL成本的影响因素
为了分析用户响应可靠程度、补偿价格和惩罚价格对IL成本的影响,采用第2组负荷进行计算。将用户的支付成本期望值除以IL中断容量得到用户的支付价格。各用户的综合价格和支付价格分别如图5和图6所示。
可见,随着补偿价格的降低、惩罚价格的升高,IL综合价格和支付价格均降低;但随着用户响应可靠程度的增大,IL综合价格降低,IL支付价格升高。
基于本文所提出的模型,会在满足约束条件的情况下优先选择IL综合价格较低的用户,即那些补偿价格较低、惩罚价格较高且响应更为可靠的用户。而用户在合同约定补偿价格和惩罚价格不变的情况下,提高响应可靠程度,有助于提高所得到的支付费用。因此按照该模型进行优化调度,对于用户而言,能够促进用户努力提高响应可靠程度,以提高参与IL项目的收益;对于电力公司而言,则有助于降低电力用户调用IL的总成本。
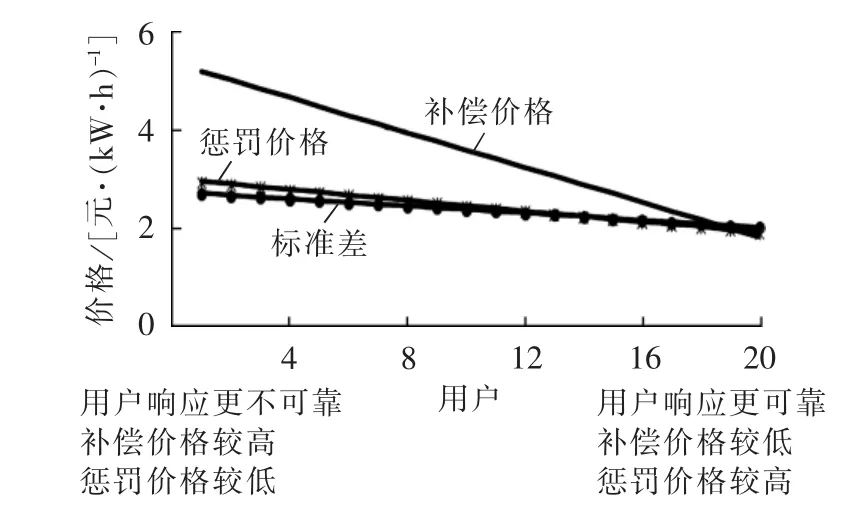
图5 IL综合价格曲线Fig.5 Total IL price curves
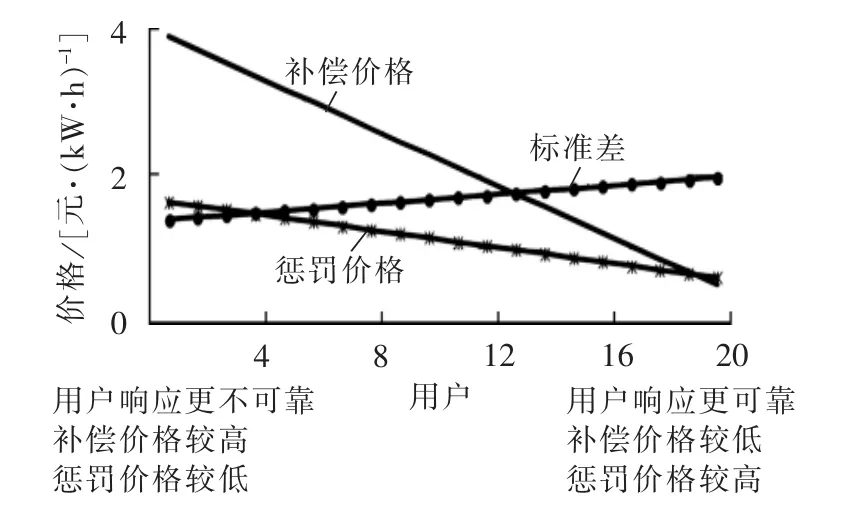
图6 IL支付价格曲线Fig.6 IL payment curves
4.5 风险系数的影响
采用第1组用户参与优化计算,当风险系数λ从0至1变化时,固定补偿成本、不确定性总成本和风险成本变化趋势见图7。随着风险系数增大,固定补偿总成本变小,风险成本变大。而当风险系数为0.5时,不确定性总成本达到最小值。

图7 权重变化时的成本变化情况Fig.7 Curves of cost vs.weight
4.6 削减需求不确定性对优化结果的影响
在削减需求均值和置信水平不变的情况下,改变削减需求的概率分布方差进行求解。削减需求的变化以时段1为例,其他时段的变化趋势相同。
削减需求方差占均值的百分比变化时成本及削减需求曲线如图8所示。可见,削减需求方差减小即削减需求的预测更为精确时,实际削减需求减少,此时相应的IL成本降低。根据本模型中的机会约束条件,提高削减需求预测准确度有助于减小削减需求,相应地减小IL成本。换言之,相同的IL总成本下提高预测准确性可以减少运行风险。
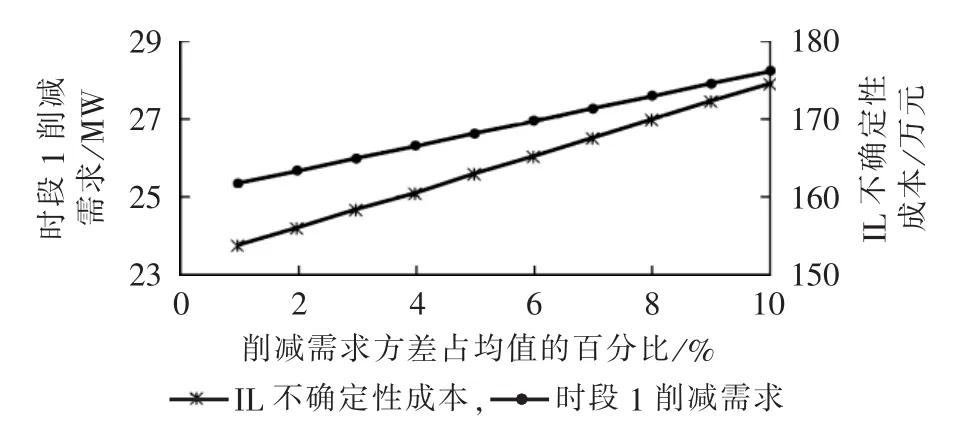
图8 削减需求方差占均值的百分比变化时成本及削减需求曲线Fig.8 Curves of cost and load-shedding requirement vs.variance-mean ratio of load-shedding requirement
5 结论
本文基于风险评估和机会约束对不确定性IL优化决策方法及其参与日前调度的流程进行研究。首先对IL的不确定性进行分析,再考虑用户响应不确定对可中断支付成本和风险成本进行建模,考虑削减需求不确定性建立机会约束模型,提出不确定性IL优化决策模型,最后给出算例分析。可得以下结论。
首先,IL参与日前调度有助于解决由于系统供电不足和机组爬坡能力不足导致的容量缺额。
其次,所提出的模型采用考虑不确定性的IL支付成本和考虑不确定性的IL风险成本之和作为目标函数,优化结果能更为合理地反映受用户响应不确定性影响的IL总成本,使电力公司调用IL总成本的期望值最低。根据所提出模型的特点,在进行优化计算前,可首先计算出每个用户IL支付成本期望值和风险成本,避免了在优化过程中采用蒙特卡洛法带来的巨大计算量。
第三,用户响应可靠程度较高时,用户获得的IL支付金额较高,并能降低电力公司调用IL的总成本,从而促使用户积极提高IL响应可靠性。相同的IL总成本下提高削减需求预测准确性可以减少运行风险,这有助于促使电力公司努力提高负荷和出力的预测准确度。
随着需求侧管理和需求响应的作用逐渐受到重视并获得了更多的政策支持,IL的应用将越来越广泛。在本文研究的基础上,更为深入地探讨IL项目的各种不确定性因素的影响,将有助于IL在调峰、降低阻塞和新能源消纳等方面发挥更大的作用。
参考文献:
[1]张钦,王锡凡,王建学,等.电力市场下需求响应研究综述[J].电力系统自动化,2008,32(3):97-106.ZHANG Qin,WANG Xifan,WANG Jianxue,etal.Surveyof demand response research in deregulated electricity markets[J].Automation of Electric Power Systems,2008,32(3):97-106.
[2]杨彦,陈皓勇,张尧,等.计及分布式发电和不完全信息可中断负荷选择的电力市场模型[J].中国电机工程学报,2011,31(28):15-24.YANG Yan,CHEN Haoyong,ZHANG Yao,et al.An electricity market model with distributed generation and interruptible load under incomplete information[J].Proceedings of the CSEE,2011,31(28):15-24.
[3]刘小聪,王蓓蓓,李扬,等.智能电网下计及用户侧互动的发电日前调度计划模型[J].中国电机工程学报,2013,33(1):30-38.LIU Xiaocong,WANG Beibei,LI Yang,et al.Day-ahead generation scheduling modelconsidering demand side interaction under smart grid paradigm[J].Proceedings of the CSEE,2013,33(1):30-38.
[4]张国新,王蓓蓓.引入需求响应的电力市场运行研究及对我国电力市场改革的思考[J].电力自动化设备,2008,28(10):28-33.ZHANG Guoxin,WANG Beibei.Study of power market operation with demand response and consideration ofChina’s power marker reform[J].Electric Power Automation Equipment,2008,28(10):28-33.
[5]刘宝碇,彭锦.不确定理论教程[M].北京:清华大学出版社,2005:序言.
[6]张颖,张有兵,曹一家,等.基于证据理论的可中断负荷不确定性风险收益评估模型[J].电力系统保护与控制,2009,37(16):1-6.ZHANG Ying,ZHANG Youbing,CAO Yijia,et al.An evaluating model of interruptible load uncertain risks and returns based on evidence theory[J].Power System Protection and Control,2009,37(16):1-6.
[7]王金凤,李渝曾,张少华.基于机会约束规划的可中断负荷管理[J].电力系统及其自动化学报,2008,20(2):42-45.WANG Jinfeng,LI Yuzeng,ZHANG Shaohua.Interruptible load management based on chance-constrained programming[J].Proceedings of the CSU-EPSA,2008,20(2):42-45.
[8]KHORSAND M A,HEYDARI H,ZAKARIAZADEH A.Interruptible load participation asoperating reserve in jointenergy and spinning reserve markets using stochastic security analysis[C]//The 2nd International Conference on Computer and Automation Engineering(ICCAE).Singapore:[s.n.],2010:8-12.
[9]OH SC,D’ARCY JB,ARINEZ JF,etal.Assessmentof energydemand response optionsin smartgrid utilizing the stochastic programming approach[C]//Power and Energy Society General Meeting,2011 IEEE.San Diego,CA,USA:IEEE,2011:1-5.
[10]于娜,芙蓉薇.电力市场高峰时段可中断负荷优化购买模型[J].电力系统及其自动化学报,2010,22(4):89-93.YU Na,FU Rongwei.Optimization model of interruptible load dispatch during the peak load time periods in the earlier power market[J].Proceedings of the CSU-EPSA,2010,22(4):89-93.
[11]刘新东,陈焕远,姚程.计及大容量燃煤机组深度调峰和可中断负荷的风电场优化调度模型[J].电力自动化设备,2012,32(2):95-100.LIU Xindong,CHEN Huanyuan,YAO Cheng.Economic dispatch consideringdeep peak-regulation and interruptibleloadsfor power system incorporated with wind farms[J].Electric Power Automation Equipment,2012,32(2):95-100.
[12]李丹,刘俊勇,刘友波,等.风电接入后考虑抽蓄-需求响应的多场景联合安全经济调度模型 [J].电力自动化设备,2015,35(2):28-34.LI Dan,LIU Junyong,LIU Youbo,et al.Joint secure&economic dispatch considering wind power,pumped storage and demand response[J].Electric Power Automation Equipment,2015,35(2):28-34.
[13]李海英,李渝曾,张少华.一种激励相容的输电阻塞管理模型[J].中国电机工程学报,2006,26(19):36-40.LI Haiying,LI Yuzeng,ZHANG Shaohua.An incentive compatible model for transmission congestion management[J].Proceedings of the CSEE,2006,26(19):36-40.
[14]FAHRIOGLU M,ALVARADO F L.Designing incentive compatible contracts for effective demand management[J].IEEE Transactions on Power Systems,2000,15(4):1255-1260.
[15]王蓓蓓,李义荣,李扬,等.考虑响应不确定性的可中断负荷参与系统备用配置的协调优化[J].电力自动化设备,2015,35(11):1-8.WANG Beibei,LI Yirong,LI Yang,et al.Optimal coordination between system reserve and interruptible loads with response uncertainty[J].Electric Power Automation Equipment,2015,35(11):1-8.
[16]NIU W,LI Y.Uncertain optimization decision of interruptible load in demand response program[C]//2014 IEEE Innovative Smart Grid Technologies-Asia(ISGT Asia 2014).Kuala Lumpur,Malaysia:[s.n.],2014:675-679.
[17]杨胜春,刘建涛,姚建国,等.多时间尺度协调的柔性负荷互动响应调度模型与策略[J].中国电机工程学报,2014,34(22):3664-3673.YANG Shengchun,LIU Jiantao,YAO Jianguo,et al.Model and strategy for multi-time scale coordinated flexible load interactive scheduling[J].Proceedings of the CSEE,2014,34(22):3664-3673.
[18]牛文娟,王磊,李扬.需求响应项目中用户基线负荷计算方法及其应用[J].东南大学学报:自然科学版,2014,44(3):556-560.NIU Wenjuan,WANG Lei,LI Yang.Calculation method and application of customer baseline load in demand response project[J].Journal of Southeast University:Natural Science Edition,2014,44(3):556-560.
[19]BO R,LI F X.Probabilistic LMP forecasting considering load uncertainty[J].IEEE Transactions on Power Systems,2009,24(3):1279-1289.
[20]BILLINTON R,HUANG D.Effects of load forecast uncertainty on bulk electric system reliability evaluation[J].IEEE Transactions on Power Systems,2008,23(2):418-425.
[21]李文沅.电力系统风险评估——模型、方法和应用[M].北京:科学出版社,2006:7.
[22]ARGIENTO R,FARANDA R,PIEVATOLO A,et al.Distributed interruptible load shedding and micro-generator dispatching to benefitsystem operations[J].IEEE Transactionson Power Systems,2012,27(2):840-848.
