短时傅里叶变换在火成岩储层中裂缝识别中的应用
2016-05-23王祝文周大鹏杨晓辉王文华
郑 武, 王祝文, 向 旻, 周大鹏, 杨晓辉, 王文华
(1.吉林大学地球探测与科学技术学院,吉林 长春 130026;2.吉林大学地球科学学院,吉林 长春 130061)
短时傅里叶变换在火成岩储层中裂缝识别中的应用
郑武1,王祝文1,向旻1,周大鹏1,杨晓辉1,王文华2
(1.吉林大学地球探测与科学技术学院,吉林 长春130026;2.吉林大学地球科学学院,吉林 长春130061)
摘要:火成岩的储层具有物性差.非均质性强的特征。因此裂缝发育程度是制约火成岩油气藏的重要因素,那么如何识别火成岩储层的裂缝就成为火成岩油气藏开发的难点。通常采用双侧向电阻率的大小和差异识别裂缝,由于电阻率还受其他因素影响,故裂缝识别的分辨率不高。以辽河油田为例,利用电阻率与裂缝之间的关系,从短时傅里叶变换的原理出发,利用时-频方法来挖掘双侧向电阻率曲线的蕴含信息识别裂缝,并将常规的测井曲线识别裂缝与该方法相结合效果更佳显著。研究表明,采用汉明窗函数并取55个采样点来求取电阻率曲线频谱及幅值效果更好,其裂缝的识别度也较高。这种时频分析方法较好地解决了火成岩识别裂缝的问题,对地区火成岩油气藏的裂缝识别有一定的借鉴意义。
关键词:火成岩油气藏;双侧向电阻率;短时傅里叶变换;裂缝识别
郑武,王祝文,向旻,等.2016. 短时傅里叶变换在火成岩储层中裂缝识别中的应用[J].东华理工大学学报:自然科学版,39(1):42-47.
Zheng Wu,Wang Zhu-wen,Xiang Min,et al.2016. Short-time Fourier transform in the application of the igneous rock reservoir in fracture identification[J].Journal of East China University of Technology (Natural Science), 39(1):42-47.
火成岩储层中的勘探开发结果表明,裂缝在储层中不但是流体渗流通道,还是主要的储集空间,而且孔隙空间类型十分复杂。所以怎样用测井资料识别出裂缝是火成岩储层勘探开发的基础。现在对于识别裂缝主要是成像测井和常规测井;虽然成像测井能够提供丰富的井壁及井眼周围的信息,可以直观地从测井图像中定性地识别裂缝,但是这种方法成本高,不易大范围的应用,所以用常规的测井资料更好的识别裂缝是现在主要的任务和方向。而现在的常规测井主要是根据双侧向电阻率的大小和差异提出的(司马立强,2005),但是影响深浅双侧向幅度和差异大小的因素除了裂缝之外还有岩性(包括泥质含量)、流体性质等等,导致直接用双侧向来识别裂缝其效果不够理想,因此挖掘电阻率曲线上的隐含的信息便成了攻克这一困难的重点,而短时傅里叶变换正是对信号的一种有效的处理方法,可以直观的表述信号在时域和频域的特征(司马立强等, 2001),并且通过这些特征的显示可以更好的去识别裂缝的发育程度。
1双侧向电阻率的裂缝响应特征及其影响因素
通过物理模型模拟以及数值模型模拟,可以得出双侧向电阻率和不同产状裂缝之间的关系,并且利用这样的关系分析裂缝的发育程度。
1.1裂缝响应特征
1.1.1物理模型模拟结果
四川石油管理局测井公司于1982年在世界上第一个对不同角度的裂缝电阻率测井响应进行物理实验研究(用石蜡模拟地层的平板状裂缝)——双侧向水槽模型实验(柯式镇等,2003; 谭廷栋,1987; 赵良孝等, 1994),这一实验表明裂缝的产状与双侧向的差异有着直接的关系,双侧向测井对水平缝的测量结果呈负差异,对垂直缝的测量结果为正差异(司马立强等 2009)。

表1 裂缝产状与双侧向之间的关系
1.1.2数值模型模拟结果
斯仑贝谢公司的Sibbit等(1985)、Cuo等(2005)采用有限元法模拟出了不同角度、不同张开度的裂缝的双侧向测井响应。假设的模型为直径127 m、高102 m的圆柱体地层,对深侧向测井来讲,其范围已足够大。基岩块电阻率Rb=10 000 Ω·m,钻井液电阻率Rm=0.1 Ω·m,基岩块孔隙度为l %,相对于地层模型来说,其侵入深度趋于无限大(邓少贵等, 2005; 李善等, 1996; 史謌等,2004)。且其模拟结果也证明了物理模型模拟结果的正确性(Boyeldieu, 1982)。
1.2其它因素对双侧向电阻率的影响
这些因素有岩性(包括泥质含量)、流体性质等(谭廷栋等, 1991; 张树东, 2005)。
1.2.1岩性的影响
储层中岩石的体积占整个岩石体积的大部分或绝大部分,故岩石的导电特性将直接影响电阻率大小。表2列出了不同岩石和矿物的导电特性。

表2 主要岩石和矿物电阻率
总体来说,火成岩的电阻率大小受所含岩石和矿物电阻率的大小来决定,如玄武岩的电阻率普遍较高而流纹质凝灰岩的电阻率较低等(刘海君, 2003),故岩性的不同也是影响双侧向电阻率的重要因素。
1.2.2泥质含量的影响
泥质含量的增加将会增加岩石的导电性,同时会改变岩石的骨架结构,使其形成发达的导电网络,同时泥质的附加导电性也与矿物成分有关,阳离子交换能力强的,其附加导电能力强,对地层电阻率的影响也较大。
所以,泥质含量也会影响双侧向电阻率的差异和大小。
1.2.3流体因素
流体因素主要指钻井滤液电阻率和地层中流体的电阻率的大小和差异。由于钻井液侵入造成的冲洗带电阻率为Rxo与未侵入带电阻率为Rt之间的不同,会使测得的双侧向电阻率值产生变化,若Rt
由于流体因素的存在,使测得的双侧向电阻率值产生变化,进而会影响对研究层段裂缝发育程度的推断。
2短时傅里叶变换
由于在实际工作中所遇到的信号往往都是时变的,即信号的频率随时间变化,而传统的傅立叶变换由于其基函数是复正弦,缺少时域定位的功能,因此傅立叶变换不适用于时变信号。信号分析和处理的一个重要任务一方面是要了解信号所包含的频谱信息,另一方面还希望知道不同频率所出现的时间。而短时傅里叶变换(李振兴, 2010; 唐向宏等,2008)正具备上面的两种优点。
短时傅里叶变换的原理是在时域用窗函数去截取所要处理的信号,对截取下来的局部信号作傅立叶变换,即得在该时刻该段信号的傅立叶变换。不断地移动窗函数,即可得到不同时刻的傅立叶变换。这些傅立叶变换的集合,即为短时傅里叶变换。则给定一信号x(t)∈L2(R),其STFT定义为:
∫x(τ)g*(τ-t)e-jΩτdτ=
(1)
当要在计算机上实现一个信号的短时傅立叶变换时,该信号必须是离散的,且为有限长。设给定的双侧向信号为x(n),n=0,1,……,L-1,对应(2.1.1)式,有
(2)
式中N是在时间轴上窗函数移动的步长,ω是圆周频率,ω=ΩTs,Ts为由x(t)得到x(n)的抽样间隔。该式对应傅立叶变换中的DTFT(Cohen, 1995),即时间是离散的,频率是连续的。为了在计算机上实现,应将频率ω离散化,令
(3)
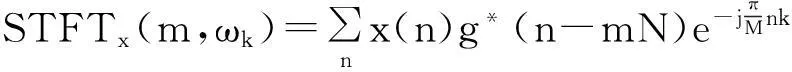
(4)
上式将频域的一个周期2π分成了M点,显然,上式是一个标准的M点DFT,若窗函数g(n)的宽度正好也是M点,那么上式可写成
(5)
若g(n)的宽度小于M,那么可将其补零,使之变成M,若g(n)的宽度大于M,则应增大M使之等于窗函数的宽度。总之,(4)式为一标准DFT,时域、频域的长度都是M点。
当对信号作时-频分析时,一般对快变的信号,希望它有好的时间分辨率以观察其快变部分(如尖脉冲等),即观察的时间宽度要小,受时宽-带宽积的影响,这样,对该信号频域的分辨率必定要下降。由于快变信号对应的是高频信号,因此对这一类信号希望有好的时间分辨率,但同时就要降低高频的分辨率。反之,对慢变信号,由于它对应的是低频信号,所以希望在低频处有好的频率分辨率,但不可避免的要降低时域的分辨率。
显然,当利用STFT时,若希望能得到好的时-频分辨率,或好的时-频定位,应选取时宽、带宽都比较窄的窗函数,遗憾的是,由于受不确定性原理(张贤达, 2001)的限制,无法做到使时宽和频宽同时为最小,所以选取合理的时窗进行时频分析可以提高裂缝识别的程度。
3裂缝储层识别应用
选择合适的窗函数进行短时傅里叶分析主要考虑的问题:(1)分辨率问题。如何选择合适的窗函数使得窗口在时域上能够尽量严格地划分信号空间,同时要求窗函数的傅里叶变换具有尽量窄的频域主瓣宽度。(2)频谱泄漏问题。对时域的窗函数作傅里叶变换后,理想情况下对应的频域窗为个单一的主瓣、旁瓣的出现会导致信号分析时的频谱泄漏。
为解决上述问题,对4种窗函数(表3)分析发现,汉明窗的频域主瓣宽度为1.30 Δw,比矩形窗多0.41 Δw,并且汉明窗的旁瓣峰值比主瓣低43 dB,同其他窗函数比较,汉明窗能够更好的解决分辨率和频谱泄露的问题,因此,本文将汉明窗作为短时傅里叶变换的分析窗。
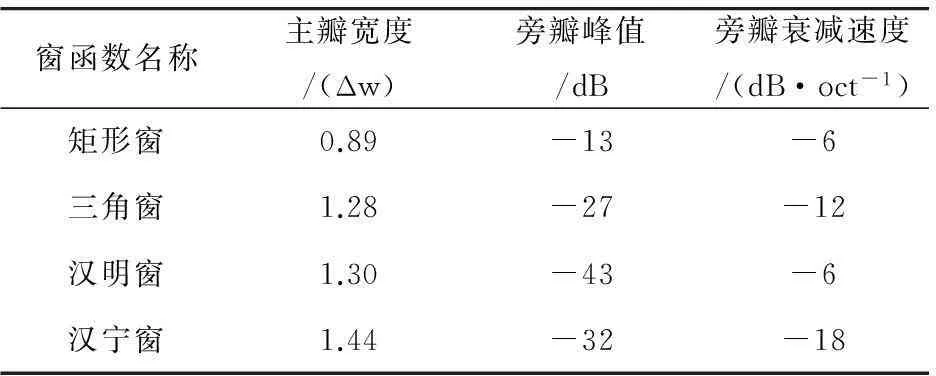
表3 常用窗函数标准值
同时为满足深度域和频率域的综合分辨能力,同时结合研究区资料并通过计算发现,采用汉明窗函数为分析的时窗、窗长为55个采样点时,STFT时频分析的效果相对较好,但是,对于幅值高低的大小要根据具体的深度段进行具体分析,才能正确地分析出裂缝发育层段。
图1为辽河油田X1井的双侧向电阻率的时-频分析图(3 460 ~3 500 m),图中3 477~3 480 m的深度段的幅值在10 dB以上,明显高于图上其它深度段的幅值,即该深度段上的电阻率曲线差异性较大,表明该段为裂缝发育段。
在3 460~3 500 m深度段(图2),其岩性是上下两大段玄武岩中间夹着一段细砂岩,再对常规测井曲线分析发现,其井径规则,自然伽马值在3 475~3 480 m和3 492~3 495 m处有明显的波动,三孔隙度曲线也有明显的小范围波动,电阻率曲线也存在较小的正异常,推测可能是中间这段砂岩造成的,但这些差异仍然不能够很好地突出该深度段上裂缝的发育情况,也无法知道到底哪段发育,哪段不发育。
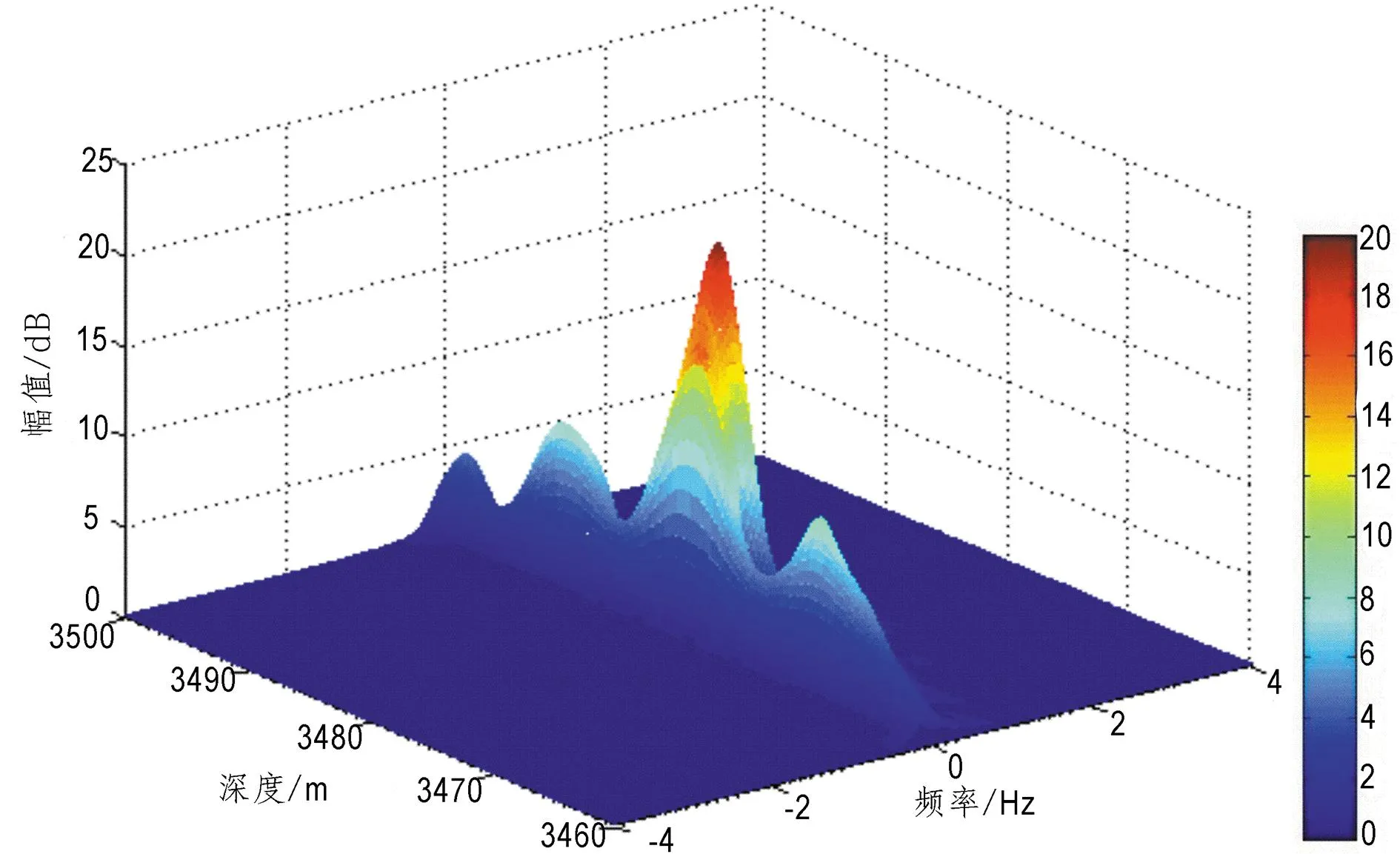
图1 X1井时频分析图Fig.1 X1 well time-frequency analysis plot
但在时频分析图中,3 475~3 480 m表现为较高的幅值,可知在该段电阻率曲线发生了变化,正是这些变化指示了裂缝的发育程度。进而推测该段相比其它深度段来说,为裂缝的发育段。而试油资料表明在3 475~3 482.4 m层段,其日产油52.8 m3,试油结果为工业油层。对比试油分析结果与时-频分析的解释结果发现深度段几乎一致,所以也证明了时频分析结果的正确性。
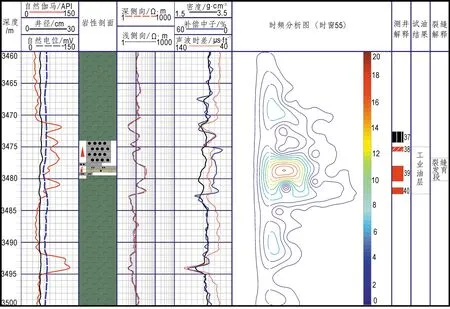
图2 X1井3460-3500m常规测井曲线与时-频分析综合解释图Fig.2 The comprehensive interpretation graph of common well logging and time-frequency analysis in 3460-3500m X1 well
同时利用时频分析方法也确定了3 475~3 480 m为裂缝发育层段,而3 492~3 495 m并不是裂缝发育段,所以将常规测井资料与时频分析方法相结合能够更好的对研究层段进行裂缝识别。
通过对辽河油田X2井3 760~3 808 m的深度段进行分析发现(图3),其井径规则,自然伽马值较高,且在3 785~3 790 m处存在一个极值,双侧向电阻率也较为稳定,且在同样的深度段有明显的正差异出现,三孔隙度曲线在该深度段波动较为明显,但是这些特征并没有很好的表明该段到底是否为裂缝发育段。
从时-频分析图中可以发现,其时-频分析的结果显示在3 788~3 793 m处幅值较高,表明电阻率曲线差异性较大,证明该深度段有一定的裂缝发育,并能够形成较好地储层。而试油结果显示在3 760~3 808 m,其日产油50.18 t,气46 893 m3,累计产油51.57 t,气71 908 m3,试油结论为气层,再对比时-频分析图与试油结果可知,两者的深度段大体一致,也证明了时频分析的正确性,同时还说明在这个深度段很有可能是该储层的成藏区域。
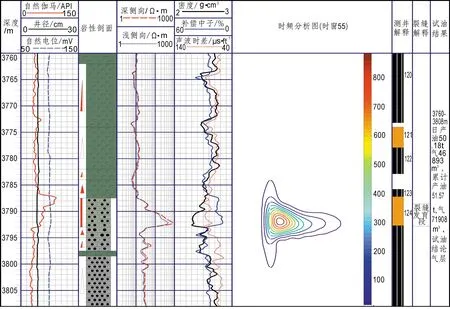
图3 X2井3 760~3 808 m常规测井曲线与时-频分析综合解释图Fig.3 The comprehensive interpretation graph of common well logging and time~frequency analysis in 3 760-3 808 m X2 well
总体来说,时-频分析适用于火成岩的裂缝识别,且与常规测井方法相比,对于一些利用常规测井资料无法确定该层段是否为裂缝发育段时,再结合时频分析结果可以得出更为确切的结论,说明在该研究区将常规测井识别裂缝的方法与时频分析方法相结合来识别裂缝效果较好。而且针对火成岩储层的特点,时-频分析的结果更能够突出该储层的裂缝发育段,对于接下来分析储层及裂缝都会有所帮助。
4结论
(1)由于直接用双侧向电阻率来识别裂缝时,除了裂缝的影响因素之外,还有岩性、泥质、流体因素的共同作用,导致直接识别起来效果较差,很难判断所研究深度段的裂缝发育情况,故采用短时傅里叶变换的方法研究其时域和频域的特征并与常规测井资料相结合来识别裂缝,效果更佳。
(2)对于短时傅里叶变换的时频分析的方法识别裂缝,首先是时窗和窗长的选择问题,对于不同的研究区,要经过一定的尝试才能够知道该研究区更适合什么样的时窗和窗长,才能更好地应用这种方法。
(3)通过时-频分析方法将电阻率测井曲线转化到时-频域上,突出了电阻率曲线的在时-频域的响应特征,将电阻率的信息映射在其时-频域的能量特征上,进而可以提取裂缝发育信息,分析裂缝发育段。
(4)该方法适用于火成岩储层的裂缝识别。通过分析可以给出关于该裂缝相对于该储层的一些隐含信息,更有助于以后对于该火山岩储层的研究和勘探。对于其它地区火山岩储层及裂缝研究,本文提出的方法也有一定的借鉴意义。
参考文献
邓少贵,范宜仁. 2005.致密砂岩储集层裂缝的双侧向测井响应快速算法[J].石油大学学报:自然科学版,29(3):31-34.
柯式镇,冯启,袁秀荷,等,2003.裂缝地层双侧向测井响应物理模拟研究[J].测井技术,27(5):353-356.
李善,肖承文、汪涵明,等. 1996.裂缝双侧向测井响应的数学模型及裂缝孔隙度的定理解释[J].地球物理学报,39(6):845-852.
李振兴. 2010.细化FFT的短时傅里叶变换方法[J].四川兵工学报,31(2):133-135.
刘海君. 2003.火成岩岩性分析与含油气性关系[D].大庆石油学院.
史謌,何涛,许岳奇,等.2004.用正演数值计算方法开展双侧向测井对裂缝的响应研究[J].地球物理学报,47(2):359-363.
司马立强,疏壮志. 2009.碳酸盐岩储层测井评价方法及应用[M].北京:石油工业出版社.
司马立强,杨洪鹏. 2001. 基于时频分析的储层裂缝识别方法[J].成都西南石油大学, 35(4):331-334.
司马立强. 2005.碳酸盐岩缝-洞性储层测井综合评价方法及应用研究[D].成都:西南石油大学.
谭廷栋. 1991.测井资料在油田开发中的应用[M].北京:石油工业出版社.
谭廷栋.1987.裂缝性油气藏测井解释模型与评价方法[M].北京:石油工业出版社.
唐向宏,李齐良. 2008.时频分析与小波变换[M].北京:科学出版社.
雍世和,张超谟. 1996.测井数据处理与综合解释[M].北京:石油大学出版社.
张树东. 2005.复杂高电阻率碳酸盐储层深浅侧向的解释讨论[J].测井技术, 29(1):33-35.
张贤达,保铮. 2001.非平稳信号分析与处理[M].北京:国防工业出版社.
赵良孝,补勇. 1994.碳酸盐岩储层测井评价技术[M].北京:石油工业出版社.
Sibbit A M,Faivre O.1985.The dual laterolog response in fracture rocks[J]. SPWLA 26th.
Boyeldieu C, Winchester A. 1982. Use of the Dual Laterlog for the Evaluation of the Fracture Porosity in Hard Carbonate Formations. Offshore south East Aisa conference[J]. Society of Petroleum Engineers.
Guo J,Zhao J, Chen L,et al. 2005. The Stimulation Technology Research and Application in the Heavy-Oil Carboneate Recsvroir of the Facture and Cavity[J]. SPE97712.
Cohen L. 1995.Time-Frequency Analysis[M].New Jersey:Prentice Hall PTR.
Short-time Fourier Transform in the Application of the Igneous Rock Reservoir in Fracture Identification
ZHENG Wu1,WANG Zhu-wen1,XIANG Min1,ZHOU Da-peng1,YANG Xiao-hui1,WANG Wen-hua2
(1. College of Geoexploration Sci.&Tech., Jilin University, Changchun JL 130026, China;2. College of Earth Sciences, Jilin University, Changchun,JL 130061, China)
Abstract:The volcanic rock reservoir is poor physical property and heterogeneity is strong. So the degree of fracture development is an important factor of restricting the volcanic rock reservoirs, and then it would become the difficulty of the development of volcanic rock reservoirs that how to identify the volcanic reservoir cracks. The size and difference of dual laterolog resistivity are commonly used to identify fractures. But it is also affected by other factors,so the resolution of fracture identification is not high. In Liaohe oilfield as an example, using the relationship between the resistivity and crack, starting from the principle of short-time Fourier transform, using the time-frequency dual lateral resistivity curve method to mining of implicit information to identify cracks, the effect is better that the method combined with conventional logging curve to identify cracks and that. It is shown that its effect is better with using the hamming window function and take 55 samples to calculate the resistivity curve of spectrum and amplitude, and the fracture identification degree also is higher. The time-frequency analysis method is better solved the problem of the volcanic rock identification of fracture, and volcanic rock reservoirs has a certain reference significance in other areas of fracture identification.
Key Words:volcanic rock reservoirs; dual lateral resistivity; short-time Fourier transform; fracture identification
中图分类号:P631.81
文献标识码:A
文章编号:1674-3504(2016)01-0042-06
doi:10.3969/j.issn.1674-3504.2016.01.007
作者简介:郑武(1990—),男,硕士,主要研究地球物理学测井方向。E-mail:1034208000@qq.com通讯作者:王祝文( 1961—),男,教授,博士生导师,主要从事地球物理测井新方法新技术、以及复杂岩性的地球物理测井解释和评价、核地球物理、辐射与环境评价等方面的教学和科研工作。 E-mail:wangzw@jlu.edu.cn
基金项目:国家973项目“辽河盆地东部凹陷火成岩分布特征与典型区解剖研究》”(2012CB822002)
收稿日期:2015-09-19
