考虑电压约束的分布式电源接入配电网最大准入容量计算方法
2016-05-22刘科研刘永梅盛万兴孟晓丽
刘科研,刘永梅,盛万兴,孟晓丽
(中国电力科学研究院,北京 100192)
0 引言
分布式电源(DG)的接入给配电网的运行带来了一系列的影响:一方面它能够改善网络电压质量、降低网络损耗;另一方面当分布式电源接入渗透率较高时可能会影响网络的安全运行。对于分布式电源接入配电网的最大渗透率计算,传统的研究主要集中在给定分布式电源接入点和接入数量下分布式电源所能接入网络的最大渗透率[1]。这是一个最优规划问题,所求解的是分布式电源的最优接入方式,目标是接入容量最大。这种应用场景主要出现在分布式电源即将接入配电网前的规划阶段。但是如果从配电网的角度来看,在所求解的最大接入容量下,当分布式电源接入的位置和容量改变时,无法保证网络约束不越限。
因此,在分布式电源接入位置、数量、容量未知时,评价配电网所能接纳的分布式电源最大渗透率就无法采用前面所述的模型和方法求解[2-5]。在这种情况下求解的最大渗透率相对于以分布式电源接入容量最大为目标所求解的最优值是一个更为保守的值。因为在该渗透率下,不管分布式电源以何种方式接入均应保证网络各项约束不越限,而不只是存在某一种接入方式使得约束不越限,因此需要建立一种新的数学模型,从配电网侧讨论其接纳分布式电源的最大渗透率问题。
本文在研究分布式电源接入配电网的最大渗透率时,从配电网侧的角度出发,在考虑节点电压约束的前提下建立了计及负荷不确定性的分布式电源接入配电网最大准入容量的双层规划数学模型,最后给出了求解算法。该问题的求解有助于在分布式电源接入配电网前,对配电网整体的分布式电源接纳能力做出评估,在求解得到的最大渗透率下,无论分布式电源接入位置、数量、容量如何,网络均能安全运行。
1 配电网负荷及分布式电源有功出力数学特性
1.1 配电网负荷数学特性
配电网中的负荷一般具有较强的时序特性,但是从中长期的负荷数据来看,配电网负荷的概率分布基本符合正态分布模型,其正态密度函数描述如下[6]:
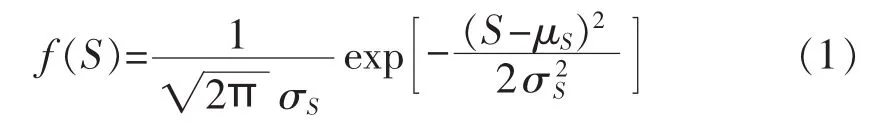
其中,σS、μS分别为基于统计数据的负荷视在功率的方差和均值。在本文中,将负荷的不确定性描述为区间的形式,即,其中 S和 S分别为负荷某一时段历史数据中的最小值和最大值。在网络正常运行时,负荷的取值可能为其区间中的任意值。
1.2 分布式电源有功出力数学特性
目前接入配电网中的分布式电源主要为风电机组和光伏机组,二者一次能源均为可再生能源,因此都具有较强的随机特性。
风电机组的风轮从风中吸收能量并将其转化成电能的数学式如下:
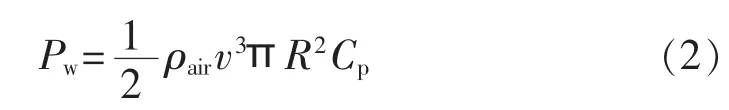
其中,Pw为输出功率;ρair为空气密度;v为风速;R为风轮扫风面的半径;Cp为功率系数。风电机组输出功率与风速的三次方成正比,受风速影响很大。而风速概率分布一般满足两参数Weibull分布的概率密度函数:
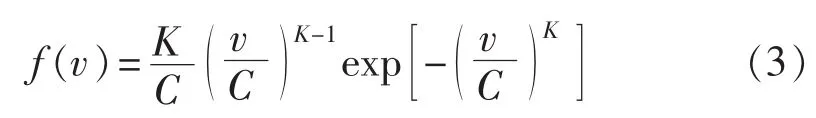
其中,K为形状参数,反映风速分布的特点;C为尺度参数,反映该地区平均风速的大小。
太阳能光伏发电系统主要由太阳能电池方阵、控制器和逆变器组成,其中,太阳能电池方阵是核心部件。太阳能电池方阵的输出功率为:

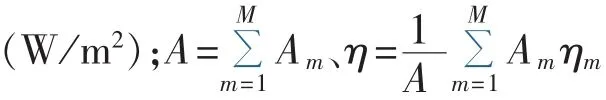
太阳光照辐射度r在一定时间段内可以近似服从Beta分布,其概率密度函数为:
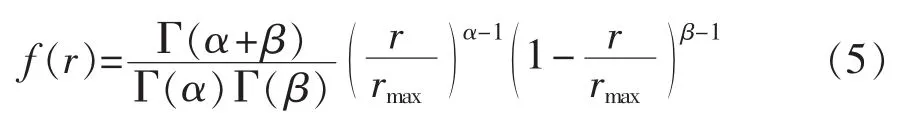
其中,rmax为最大辐射度;α、β均为Beta分布形状参数。
由式(4)、(5)可得 Psolar的概率密度函数:

其中,Psolar,max=rmaxAη为太阳能电池方阵最大输出功率。光伏发电系统一般只向电网提供有功功率,其无功功率可以不予考虑。
2 分布式电源最大准入容量计算的数学模型及求解方法
2.1 分布式电源最大准入容量数学模型
本文所提出的最大准入容量并非一般意义上满足各项约束下所能接入的最大容量。准入容量是指在接入网络的分布式电源总容量小于该容量值时,能满足各分布式电源以任何位置、任何容量接入网络均不会造成网络约束越限。一般而言,对于特定的网络通过其历史数据可以获得各节点负荷的分布图。按前文所述,在这里将负荷的不确定性以变化区间的形式表示,即认为负荷是在某一区间随机变化的。
影响分布式电源接入配电网的因素有多种,本文仅考虑分布式电源接入网络的节点电压约束问题,即系统电压幅值以及线路潮流约束。综上所述,可以得到计及负荷不确定性及节点电压约束的分布式电源最大准入容量的数学模型:

其中,M为待确定的准入容量值;分别为节点i所允许的电压幅值上限和下限;Ui为节点i的电压幅值;分别为节点i在准入容量下负荷变化时不同分布式电源接入方式所能产生最高电压幅值和最低电压幅值;Sij、Pij、Qij分别为 i-j支路上流过的视在功率、有功功率和无功功率;Gij、Bij为节点导纳矩阵中所对应的元素。其中的潮流等式约束、负荷区间约束和分布式电源有功出力约束具体如式(8)所示。
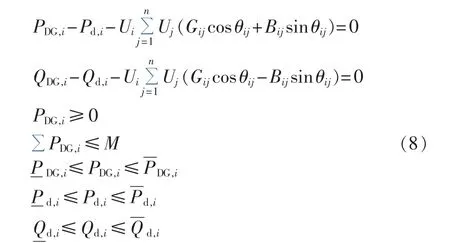
其中,PDG,i、Pd,i、Qd,i分别为节点 i处所接 DG 有功出力及有功、无功负荷;分别为有功、无功负荷区间的最小值;分别为有功、无功负荷区间的最大值。
将式(7)和式(8)模型简化为式(9)所示的简单数学模型:

其中,x、p、s分别为网络状态量、各分布式电源待接入节点接入的分布式电源有功和各节点负荷值;为各负荷的区间,和分别对应有功、无功负荷区间的最小值和最大值;等式约束 f(x,p,s)=0 为潮流方程,g(x)≤0为网络的安全约束,包括节点电压幅值上下限约束和支路功率约束,C为约束的个数,j=1,…,C。数学模型中不等式约束的物理意义为当网络中接入分布式电源有功小于M时,无论负荷在各自区间怎样变化,各项约束均不会越限。
通过式(9)所确定的分布式电源最大准入容量具有重要意义,其本质是网络的最大安全负功率接入量。考虑到配电网中分布式电源的出力通常是随机性的,因此不论各分布式电源出力如何变化,接入网络的总有功功率总是小于分布式电源总额定容量值。若接入网络的分布式电源额定容量总值不超过准入容量值,不论各分布式电源出力随机性如何,网络均处于安全状态。所以式(9)实际上也间接地包含了分布式电源出力不确定的情况。
式(9)并非一般的约束优化问题,而是属于双层优化的问题,目前并没有通用的求解算法[7],但是对于某些特殊形式的双层优化问题可以通过一系列的变换来寻求求解方法。现构造式(10):
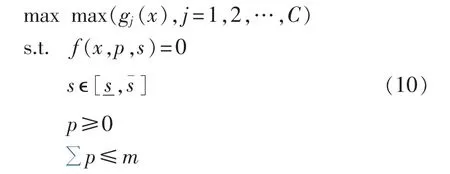
对于式(10),当给定m的值时,便可以求出该优化问题的最优值。式(9)即转变成寻求最大的m,使得 φ(m)≤0。
进一步,式(10)可以分解为如下C个子优化问题,其中 j=1,2,…,C:
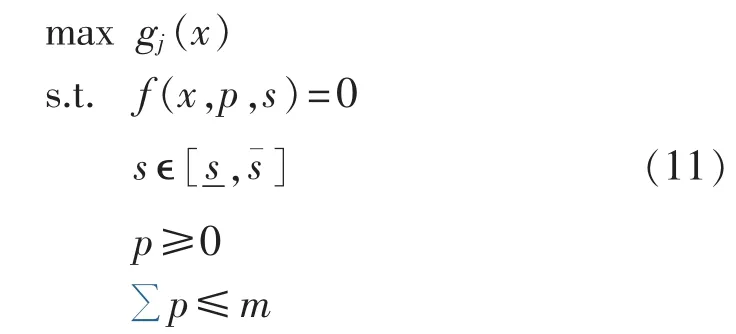
将第j个子优化问题的最优值定义为φj(m),则φ(m)=max(φ1(m),…,φC(m))。 若 k 是最大的 φj(m)值对应的脚标,则第k个子问题的最优解即对应着式(10)的最优解。这也说明第k个约束是最容易越限的一个约束,对应到原电力网络为此时网络的最薄弱环节。
可以证明函数φ(m)是连续且单调递增的函数,限于篇幅,证明过程省略。根据函数φ(m)的连续且单调递增的特性,原来的式(9)即转变为寻找φ(m)=0的解。
为求解方程 φ(m)=0,本文利用函数 φ(m)连续且递增的性质,采用一种简单的二分方法来求出m的值。
(1)设定方程的精度ε(ε为一个较小的正数)。确定方程解所在的大致区间[tn,tp],满足 φ(tp)≥0,φ(tn)≤0。
(2) 求解 φ((tn+tp)/2)的值,若求得的值为负则取 tn=(tn+tp)/2;否则取 tp=(tn+tp)/2。
(3) 判断是否成立,若成立则方程φ(m)=0的解为 m=tn,计算完成;若不成立,则转步骤(2)。
根据分布式电源接入配电网络的实际经验,可以选取初始的。其中为网络最大的总有功负荷值,此时各负荷取其变化区间的最大值,在大多数电力系统中当m取该值时,对应的 φ(m)>0。
2.2 基于信赖域的序列二次规划算法
求解约束优化问题的常用算法有逐次线性规划法[8]、序列二次规划法[9-11]、原对偶内点法及其改进算法[12-15]等算法,但是各算法都有一定的局限性。本文提出采用基于信赖域思想的序列二次规划算法来求解约束优化问题,其继承了传统序列二次规划法收敛速度快的特点,并且加上了信赖域指导的方法来防止因迭代步长过大而导致数值振荡甚至不收敛的问题。
2.2.1 信赖域方法的基本原理
信赖域方法的基本思想是:首先给定一个信赖域半径作为位移长度的上界,并以当前迭代点为中心、以此上界为半径确定一个称为信赖域的闭球区域。然后,通过求解该区域内的信赖域子问题(目标函数的二次近似模型)的最优点来确定候选位移。若候选位移能使目标函数值有充分的下降量,则接受该候选位移作为新的位移,并保持或扩大信赖域半径,继续新的迭代;否则,说明二次模型与目标函数的近似度不够理想,需要缩小信赖域半径,再通过求解新的信赖域内的子问题得到新的候选位移。如此重复下去,直到满足迭代终止条件。
对于无约束优化问题:

设 xk是第 k 次迭代点,记 fk=f(xk),gk=f(xk),Bk=△2f(xk),则第k次迭代步的信赖域子问题具有如下形式:
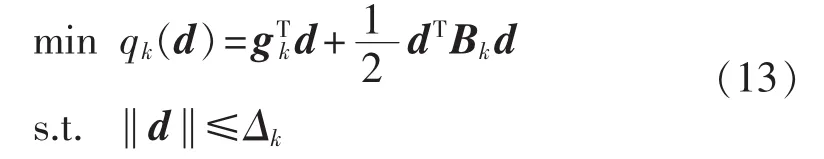
其中,qk(d)为函数 f(x)在xk处以 d 为步长的预测增量;Δk为信赖域半径;‖·‖为任一种向量范数,通常取2-范数或∞-范数。
定义Δfk为f(x)在第k步的实际下降量:

定义Δqk为对应的预测下降量:
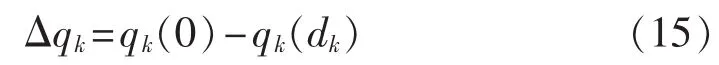
定义Δfk和Δqk的比值为:

通常情况下,有 Δqk>0。 因此,若rk<0,则 Δfk<0,xk+dk不能作为下一个迭代点,需要缩小信赖半径重新求解问题;若rk比较接近于1,说明二次模型与目标函数在信赖域范围内有很好的相似性,此时xk+1=xk+dk可以作为新的迭代点,同时下一次迭代时可以增大信赖半径;对于其他情况,信赖半径可以保持不变。
2.2.2 约束优化问题的信赖域序列二次规划法
对于约束优化问题式(11)可以表述为式(17):
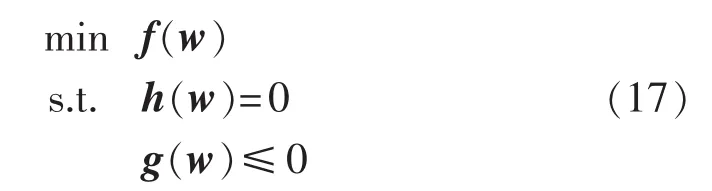
其中,w 为式(11)中各变量;等式约束 h(w)=0 对应潮流方程,不等式约束g(w)≤0对应约束不等式。
采用外罚函数的方法将式(17)改写为无约束优化问题,定义价值函数 Pσ(w):
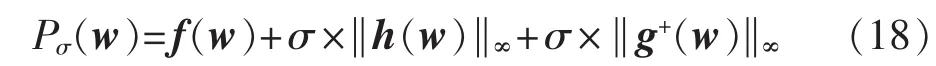
其中,σ为约束惩罚系数,当σ足够大时无约束问题式(18)的解即为约束优化问题式(17)的解;g+(w)表示对于约束函数中的每一项有。令当前迭代点为wk,信赖域半径为Δk,惩罚系数为σk。则第k次迭代的信赖域内子二次规划问题模型为:
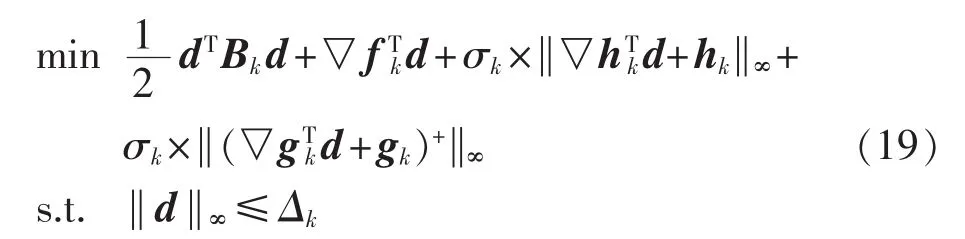
Bk为原目标函数的海森矩阵,d为需要求解的本次迭代最优步长。由于式(19)中还含有无穷范数,将式(19)进一步等效为式(20)形式。
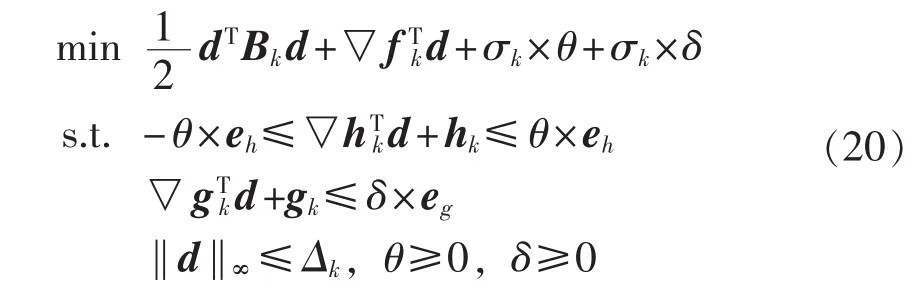
其中,θ、δ为人工添加的正变量用以等效无穷范数形式,事实上式(20)的最优解满足,均为单位列向量,二者行数分别为等式约束个数和不等式约束个数。考虑到实际潮流等式的一阶方程组总能有解,因此可以将θ变量去除,将式(20)进一步简化为如下形式:

求解式(21)得到最优步长d后,需要对步长和当前信赖域半径进行判断。在此定义原目标函数的二阶泰勒展开式Φ(d)为:
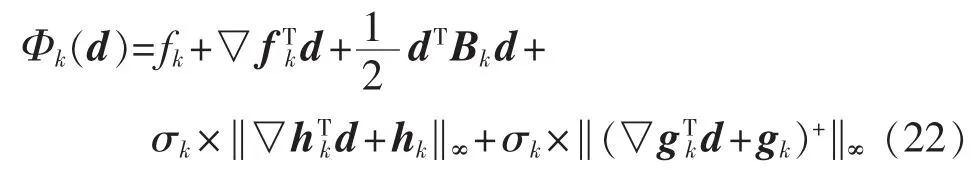
定义参数rk来表征当前步长下实际目标函数改进值和二阶模型函数的改进值的比值:

若rk越接近1,则表明在当前步长下,二阶模型函数能够很好地拟合实际目标函数,在这种情况下可以接受当前步长并增大信赖域半径和罚参数;反之则考虑拒绝步长并减小信赖域半径。参考经典无约束优化问题的信赖域指导方法,采取如式(24)所示的信赖域指引方法:

其中,分别为预设的最大罚参数和信赖域半径。若在当前迭代点处信赖域内,所求解的子二次规划问题得到步长矢量的无穷范数小于设定的精度值且罚参数达到指定最大值时,即认为已达到最优点。采用式(24)所示的信赖域指导方法能够自适应的调节信赖域半径,以使原优化问题快速地收敛至最优点。
求解约束优化问题的信赖域序列二次规划法如图1所示。
3 分布式电源接入配电网最大准入容量计算流程
综合前述内容,可将分布式电源接入配电网最大准入容量的计算流程归结如下。
a.根据系统各节点负荷的历史数据,统计各节点负荷有功、无功的波动区间。
b.令 k=1,设定和最大准入容量的计算精度 ε。 令 tn=rk,tp=rk+1。
c.令分布式电源准入容量为 M=rk+2=(tn+tp)/2,计算在该准入容量下负荷在其区间内变化时各节点负荷所能达到的最大和最小值以及各线路输送功率容量的最大值,即求解式(11)。
d.利用2.2节所述的信赖域序列二次规划法求解式(11)。
e.统计系统约束越限最大值,即对应φ(M)=max(φ1(M),…,φC(M)),其中 C 为系统节点电压幅值约束和线路输送容量约束的个数。
f.若φ(M)>0则说明在该准入容量下,系统约束可能会越限,应降低准入容量值,令tp=M;反之则说明在当前准入容量下,系统约束不可能越限,应提高准入容量值,令tn=M。

图1 信赖域序列二次规划法Fig.1 Flowchart of trust region sequential quadratic programming algorithm
g.判断是否成立,若成立则系统分布式电源的最大准入容量值为tn,计算完成;若不成立,则转步骤c。
4 算例分析
本章以IEEE 33节点系统为例计算,通过本文提出算法计算该系统接入分布式电源的最大准入容量。设定系统最高允许电压幅值为12×1.07=12.84(kV),最低允许电压幅值为12×0.93=11.16(kV)。对IEEE 33节点系统闭合联络支路前后进行仿真,仿真软件为MATLAB,对比仿真结果并对其进行分析。求解最大准入容量的仿真精度为10-3MW。
IEEE 33节点系统单线图如图2所示,虚线为系统的联络线。由于本文考虑了负荷的波动特性,因此增加了负荷数据的变动区间,定义了3种负荷区间类型,系统各节点负荷区间类型及区间最大、最小值(均为标幺值)见表1。

图2 IEEE 33节点系统图Fig.2 Diagram of IEEE 33-bus system
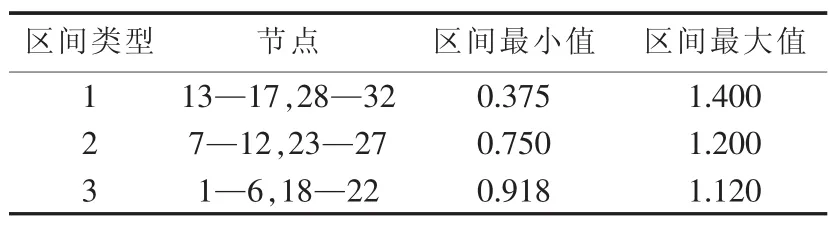
表1 系统各节点负荷区间类型及区间值Table 1 Load variation types and ranges of system nodes
对开环的IEEE 33节点系统进行仿真并记录迭代过程,如表2所示。其中,k为迭代次数;rk为第k次迭代时计算的准入容量值;φ(rk)为准入容量值为rk时的最大约束越限值,若其值小于零则表示该准入容量值下不会出现网络安全约束越限,反之则会出现安全约束越限;越限节点/支路表示在当前准入容量下可能会出现越限现象的节点和支路。

表2 迭代过程数据Table2 Data during iterations
表2中+0和-0分别表示大于0和小于0的极小数,由于精度关系未在表中具体写出(表3同)。系统仿真时长为40.8 s,从表2的迭代过程可以看到该系统最大DG准入容量为0.908MW。当接入系统中的DG总容量小于0.908MW时,无论系统负荷在其区间内如何变化也无论DG接入方式如何,系统均能运行在安全状态。由表2中第8—15行可知,制约DG接入容量的因素主要在于节点17的电压幅值。观察第15次迭代节点17电压幅值达到最大值时的其他变量情况,发现仿真结果中负荷均取到最小值,而DG全部接入了节点17。这表明当系统负荷全部处于低谷时,节点17接入过多的DG会导致该节点电压约束首先越限。
对闭合了所有联络支路的IEEE 33节点系统进行仿真,得到如表3所示的迭代过程数据。
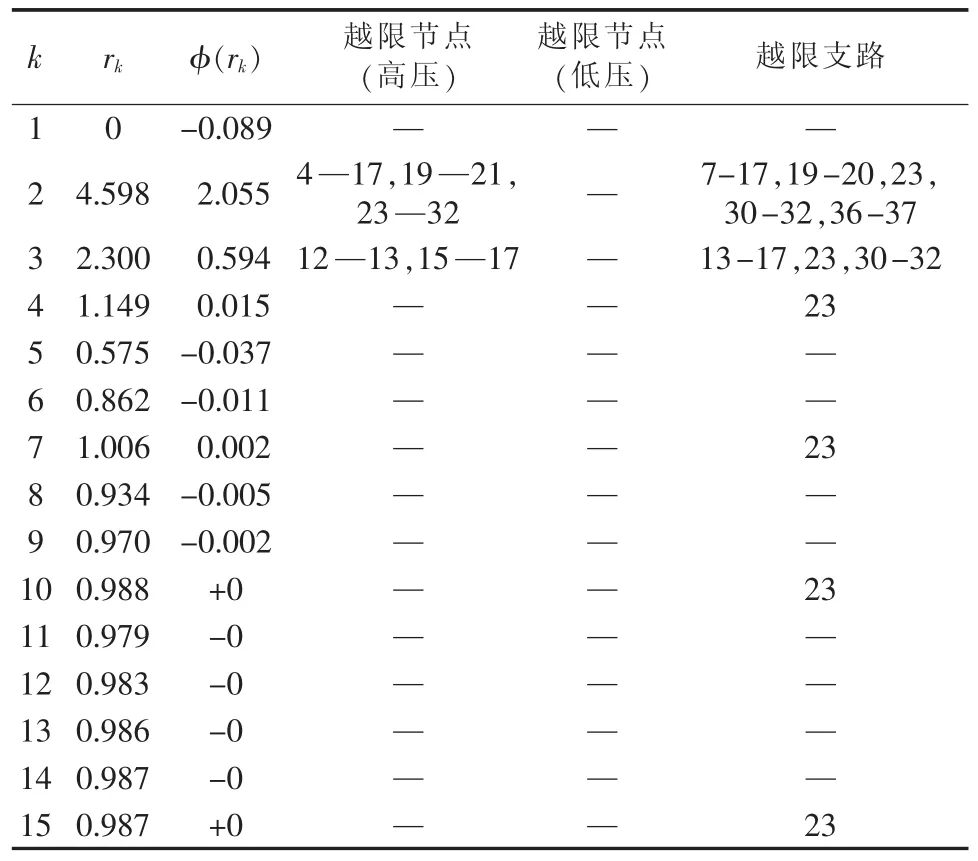
表3 迭代过程数据Table3 Data during iterations
仿真时长为52.0 s,由表3可以看出,IEEE 33节点系统闭合联络线后的DG最大准入容量为0.987MW,比闭合联络线前系统的最大准入容量增加约10%。另外,与辐射状的IEEE 33节点系统不同的是,系统最薄弱环节不再是节点电压幅值,而是支路23。增加支路23的线路容量可以增强DG接纳能力。将支路23的线路容量提高为一较高值时,如4MV·A,再次对系统进行仿真得到的结果为1.326MW,此时DG的最大准入容量得到了较大提高。通过本文的算法对系统进行DG最大准入容量仿真能够在求解过程中发现制约DG接入的系统薄弱环节,加以改进能够提高系统对于DG的接纳能力。
另外,对比IEEE 33节点系统闭合联络线前后的DG最大准入容量可以发现,环网系统由于潮流分布更为均匀,因此具有更强的DG接纳能力。
下面分析负荷的波动特性对DG最大准入容量的影响。表1所示的3种负荷区间特性,分别对应配电网负荷峰谷差极大、较大和较小3种情况。分别对3种负荷区间特性进行仿真,计算3种负荷区间特性下的DG最大准入容量。
表4所示为环网下系统所有负荷区间特性均为表1中的类型1、类型2和类型3时,DG的最大准入容量和系统接入DG的最薄弱环节。将系统负荷区间特性均设置为类型1时,系统总负荷峰值相对于原系统有了较大的提高,即使没有DG的接入,系统也将运行在安全约束越限的状态。因此进行表4的仿真时,将原系统线路容量均增加了一倍。
由表4可见,在相同网络和负荷条件下负荷区间类型1的DG最大接入容量最小,而负荷区间类型3的DG最大准入容量最大。这说明负荷的峰谷差较大时,会影响DG的最大接入容量;而负荷变化较为平稳时,系统能够接入更多的DG。
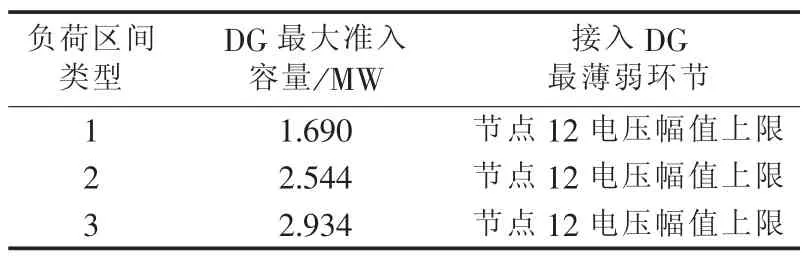
表4 不同负荷区间特性下的DG最大准入容量Table 4 Maximal allowable DG penetration capacity for different load variation types
5 结论
本文在考虑配电网负荷区间特性的基础上,采用最优化问题的形式建立了考虑节点电压约束的分布式电源接入配电网的最大准入容量的双层规划数学模型。通过变换将求解双层规划问题变成求解多次单层规划的问题,然后提出采用信赖域序列二次规划算法来求解变换后的单层规划问题。仿真结果表明本文算法能较好地求解分布式电源接入配电网最大准入容量的问题。采用本文提出算法还能对系统接入分布式电源的薄弱环节进行判断,根据仿真结果对系统进行适当改良能够提高系统接纳分布式电源的能力。另外,仿真结果还表明潮流相对均匀的环网相比辐射网有更强的接纳分布式电源能力,负荷峰谷差较小的系统比负荷峰谷差较大的系统具有更强的接纳分布式电源能力。
[1]Standards Coordinating Committee 21.IEEE standard for interconnecting distributed resources with electric power systems:IEEE Std 1547-2003[S].New York,USA:the Institute of Electrical and Electronics Engineers,Inc,2009.
[2]张沈习,李珂,程浩忠,等.间歇性分布式电源在主动配电网中的优化配置[J]. 电力自动化设备,2015,35(11):45-51.ZHANG Shenxi,LIKe,CHENG Haozhong,et al.Optimal allocation of intermittent distributed generator in active distribution network[J].Electric Power Automation Equipment,2015,35(11):45-51.
[3]徐青山,刘中泽,陈潇鹏,等.含分布式电源的配电网三相时域仿真[J]. 电力自动化设备,2015,35(8):22-30.XU Qingshan,LIU Zhongze,CHEN Xiaopeng,et al.Three-phase time-domain simulation of distribution network with distributed generations[J].Electric Power Automation Equipment,2015,35(8):22-30.
[4]栗然,马慧卓,祝晋尧,等.分布式电源接入配电网多目标优化规划[J]. 电力自动化设备,2014,34(1):6-13.LI Ran,MA Huizhuo,ZHU Jinyao,et al.Multi-objective optimization for DG integration into distribution system[J].Electric Power Automation Equipment,2014,34(1):6-13.
[5]王昌照,汪隆君,王钢,等.分布式电源出力与负荷相关性对配电网可靠性的影响分析[J]. 电力自动化设备,2015,35(6):99-105.WANG Changzhao,WANG Longjun,WANG Gang,et al.Impact of distributed generation output and load correlation on distribution network reliability[J].Electric Power Automation Equipment,2015,35(6):99-105.
[6]张喆,李庚银,魏军强.考虑分布式电源随机特性的配电网电压质量概率评估[J]. 中国电机工程学报,2013,33(13):150-156.ZHANG Zhe,LI Gengyin,WEI Junqiang.Probabilistic evaluation of voltage quality in distribution networks considering the stochastic characteristic of distributed generators[J].Proceedings of the CSEE,2013,33(13):150-156.
[7]夏成军,崔弘,王强,等.考虑静态安全约束的分布式电源准入容量计算[J]. 电网技术,2009,33(16):96-100.XIA Chengjun,CUI Hong,WANG Qiang,et al. Penetration capacity calculation for distributed generation considering static security constraints[J].Power System Technology,2009,33(16):96-100.
[8]WANG Min,LIU Shengsong.A trust region interior point algorithm for optimal power flow problems[J].International Journal of Electrical Power&Energy Systems,2005,27(4):293-300.
[9]SHENG Wanxing,LIU Keyan,CHENG Sheng,et al.A trust region SQP method for coordinated voltage control in smart distribution grid[J].IEEE Transactions on Smart Grid,2016,7(1):381-391.
[10]SHENG Wanxing,LIU Keyan,CHENG Sheng.Optimal power flow algorithm and analysis in distribution system considering distributed generation[J].IET Generation,Transmission&Distribution,2013,8(2):261-272.
[11]ALHAJRIM F,EL-HAWARY M E.Optimal distribution generation sizing via fast sequential quadratic programming[C]∥2007 Large Engineering Systems Conference on Power Engineering.[S.l.]:IEEE,2007:63-66.
[12]NEJDAWI I M,CLEMENTS K A,DAVIS P W.An efficient interior point method for sequential quadratic programming based optimal power flow [J].IEEE Transactions on Power Systems,2000,15(4):1179-1183.
[13]杨林峰,简金宝,韩道兰,等.基于最优中心参数的多中心校正内点最有潮流算法[J]. 中国电机工程学报,2012,32(4):136-144.YANG Linfeng,JIAN Jinbao,HAN Daolan,et al.Multiple centrality corrections interior point optimal power flow algorithm based on optimal centering parameter[J].Proceedings of the CSEE,2012,32(4):136-144.
[14]蔡广林,张勇军,任震.基于非线性多中心校正内点法的最优潮流算法[J]. 电工技术学报,2007,22(12):133-138.CAIGuanglin,ZHANG Yongjun,REN Zhen.Optimal power flow algorithm based on nonlinear multiple centrality corrections interior point method[J].Transactions of China Electrotechnical Society,2007,22(12):133-138.
[15]颜全椿,卫志农,孙国强,等.基于多预测校正内点法的WLAV抗差状态估计[J]. 电网技术,2013,37(8):2194-2200.YAN Quanchun,WEI Zhinong,SUN Guoqiang,et al.A robust WLAV state estimation based on multiple predictor-corrector interior point method[J].Power System Technology,2013,37(8):2194-2200.
