基于二阶锥规划的间歇性分布式电源消纳研究

邢海军，程浩忠 ，曾平良，张 逸

（1．上海交通大学 电气工程系 电力传输与功率变换控制教育部重点实验室，上海 200240；2．中国电力科学研究院，北京 100085；3．福建省电力科学研究院，福建 福州 350007）

0 引言

随着社会经济的快速发展和城市化建设的不断推进，电力需求持续增长；传统的集中式大规模发电已经不能满足电能清洁生产和能源高效利用的要求，同时还给环境保护带来了沉重的压力。这样的背景下，分布式能源特别是间歇性分布式发电IDG（Intermittent Distributed Generation）将凭借其环境友好的优点得到快速发展。

IDG接入中、低压配电网是IDG在配电网主要的消纳方式［1-4］。文献［1］利用多阶段最优潮流研究了以网损最小为目标的IDG最优消纳问题，同时讨论了以网损最小和IDG消纳最大为目标的多目标最优消纳问题。文献［2］考虑通过储能设备来提高IDG的消纳，在IDG出力过大时，通过储能装置来消纳，当IDG出力变小，储能装置放电满足负荷供电。

DG的快速发展也给配电网带来一系列的问题，如接入点电压升高、系统双向潮流、短路电流升高等。由于目前的被动管理模式，系统对DG及网络自身不加以相应的控制，导致系统无法充分利用DG在改善系统网损和电压质量等方面的积极作用，相反在某些情况下DG接入所带来的不确定性将影响系统的安全稳定运行、增加电网的经济成本。因此供电公司不得不严格控制DG的接入容量，限制DG的发电量，发生故障时也首先考虑将DG切除。

针对这种被动的管理模式，很多学者提出了主动配电网 ADN（Active Distribution Network）及主动管理AM（Active Management）的概念，并将AM应用到IDG的消纳中。文献［5-8］介绍了主动配电网的研究现状及其关键技术，分析说明了发展ADN的必要性，总结了适应ADN发展的可行技术。文献［9-10］明确了主动配电网发展面临的挑战。文献［11-14］提出了通过主动潮流管理APFM（Active Power Flow Management）来提高配电系统DG的接入容量。文献［15］提出了使用有功-无功最优潮流，并且比较了使用有功-无功最优潮流相对于仅使用有功最优潮流的优点，包括网损及无功传输的减小。文献［16］提出了2种主动潮流管理的方法，并进行了不同场景下的对比。文献［17］提出了用于AM的多时间段动态最优潮流，并考虑了储能及可控负荷对分布式能源消纳的作用。

AM就是更加细致地测量和评估配电网的系统运行数据之后，对DG和配电网设备进行实时控制并采取一定的措施进行协调。AM模式下的配电网可以采取控制DG的发出功率、调节变压器抽头和无功补偿设备等多种AM措施，使得含有DG的配电系统达到最优的运行状态，从而提高配电网对DG的消纳能力，提高配电系统的供电可靠性，改善配电网的电能质量。

本文着重分析ADN中各种AM措施。基于变压器高压侧电压、负荷及IDG的时序特性，分析DG出力切除、有载调压变压器分接头调节、无功补偿等多种AM措施对IDG消纳的影响。

1 AM

AM策略包括DG出力调度、电容器组无功补偿、有载调压变压器 OLTC（On-Load Tap Changer）抽头调节、可控负荷（需求侧响应）、网络重构等。图1是一个简单的含IDG及无功补偿电容器组的配电网络。下面通过该网络来分析DG接入对接入点电压的影响及AM对DG接入的作用。

图1 AM简单网络Fig.1 Simple network of active management

假设图中负荷功率为 PL、QL；DG（风电）注入节点 T1功率为 PDG、QDG；电容器组（C）注入节点 T1的无功为QC。节点1代表母线B10，节点2代表线路末端节点T1，线路阻抗为R+j X，变压器为OLTC，节点1电压为U1，节点2电压U2可以通过下式计算：

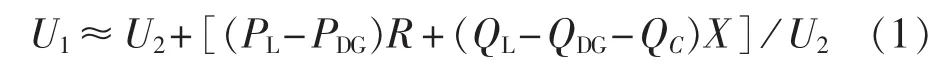
令Q=QL-QDG-QC，Q为节点2无功输出量。由式（1）可知节点2注入的间歇性功率如下：

下面以防止间歇性能源接入节点电压越限为目标来分析主动配电网的AM策略。正常运行情况下U2＞0.5U1，则 U2（U2-U1）+QX 为递增函数，由式（2）知，在负荷最小、间歇性能源出力最大时，接入节点2电压最可能越限。这也是配电网中接入DG最常见、需要解决的问题。假设节点2的电压上限为U2max，则在节点2电压达到允许上限时，间歇性能源允许的接入量为：

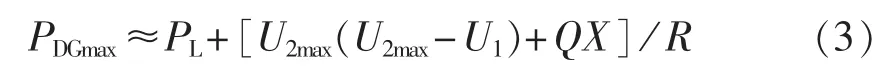
其中，PDGmax为间歇性能源允许接入的最大容量。下面分析各种AM措施下间歇性能源允许接入的最大容量。

a.DG出力调度。

允许间歇性能源运行时进行部分切机，则允许接入的最大间歇性能源如下：

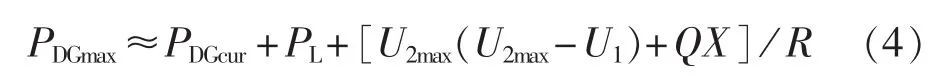
其中，PDGcur为DG允许的切除量。允许电力需求小的时段进行部分切机，可以保证接入更多容量的间歇性能源，在高峰负荷时段为电网运行提供一定支撑。

b.电容器无功补偿。

由Q=QL-QDG-QC知，要增大间歇性能源的接入量，必须使无功补偿设备由向系统提供无功变为从系统吸收无功。

由式（2）知，对于间歇性能源消纳，无功补偿效果取决于电抗X。对于架空线路（电抗较大，无避雷线架空线单导线一般约0.4Ω／km）网络，补偿效果较电缆（电抗较小，10kV三芯电缆一般约0.08Ω／km）网络好。

c.OLTC分接头调整。

由式（2）知，调节OLTC分接头，使节点1电压减小，可以增大间歇性能源的接入。最大可接入DG容量如下：

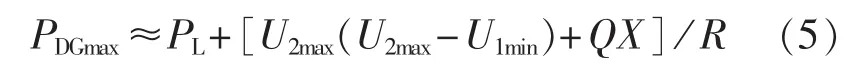
其中，U1min为OLTC调节下限时对应的节点1电压。

2 ADN中间歇性能源消纳

2.1 目标函数

本文规划模型目标函数为最小化某一时间段内总的DG切除量，具体如下：

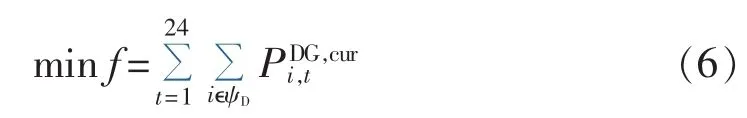
其中，f为目标函数，即最小化总的DG切除量；ψD为DG 安装节点集；为节点 i处 DG 在 t时刻的切除量。

2.2 约束条件

约束条件包括网络运行安全约束、AM约束，具体如下。

a.网络运行安全约束：

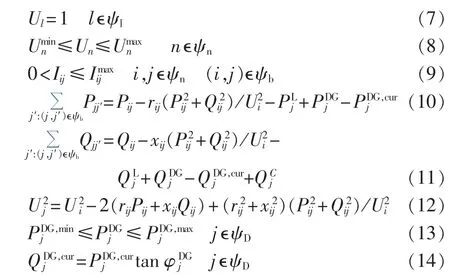
其中，ψl为变电站集；Ul为变电站节点电压；ψn为负荷节点集；分别为节点电压、电压下限及上限；ψb为支路集；分别为支路（i，j）电流及上限；j′∶（j，j′）ϵψb表示所有与节点 j相连支路的末端节点集合；分别为节点j负荷有功功率与无功功率；分别为节点j处DG原始有功出力与无功出力；分别为节点 j处 DG 切除的有功功率与无功功率；为节点j处无功补偿设备注入无功功率；rij、xij分别为支路（i，j）的电阻与电抗；Pij、Qij分别为支路（i，j）的首端有功与无功功率；Ui、Uj分别为节点 i及 j电压幅值；Pjj′、Qjj′分别为 支路（j，j′）首端的有功与无功功率；分别为节点j处DG有功出力下限与上限；为节点j处DG功率因数角。

1843年7月22日，《中英五口通商章程》在香港公布实施。章程对中英贸易过程中船钞的标准、纳税、验货、计量及货船担保等都做了详细的约定。其中，章程第六条明确规定：“凡系进口、出口货物，均按新定则例，五口一律纳税，此外各项规费丝毫不能加增。其英国商船运货进口及贩货出口，均须按照则例，将船钞、税银悉数输纳全完，由海关给发完税红单，该商呈送英国管事官验明，方准发还船牌，令行出口。”

式（7）为变电站电压等式约束；式（8）为节点电压上下限约束；式（9）为支路电流约束；式（10）、（11）为节点功率平衡约束；式（12）为节点电压约束，此处采用配电网潮流［18］；式（13）为 DG 出力约束；式（14）为DG切除有功与无功关系式。

b.AM约束：

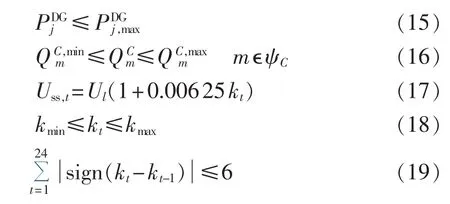
其中，为节点j处DG可以达到的最大出力，对风机而言与该时刻风速有关，即为该时刻风机的切除量；分别为无功补偿容量的下限与上限；Uss，t为变电站电压侧出口电压；Ul为变电站变压器高压侧电压；kt为t时刻OLTC触头位置，在本文第4节算例中，采用50MV·A、110±8×1.25%kV、YNd11三相双绕组变压器，电压变化范围为0.95～1.05 p.u.，所以变压器触头每档调节电压为0.00625 p.u.；kmin、kmax分别为最小及最大允许的调节位置；sign为符号函数；kt-1为t-1时刻OLTC触头位置。根据变电站实际运行经验，110 kVOLTC每天允许调节次数为6次，假定OLTC触头初始位置为0。

式（15）为 DG 实际运行功率约束；式（16）为无功补偿约束；式（17）为OLTC输出电压与触头位置等式约束；式（18）为OLTC触头调节位置约束；式（19）为OLTC实际运行约束。

2.3 二阶锥规划模型

本文ADN的DG消纳问题是混合整数非线性规划 MINLP（Mixed Integer NonLinear Programming）问题，目标函数为线性函数，约束条件包括线性及非线性函数。常规求解方法包括数学规划法及启发式算法。当考虑AM时，规划模型的求解变得非常困难、耗时，一般的求解方法较难找到最优解。本文采用凸规划理论，基于二阶锥规划SOCP（Second-Order Cone Programming）对该问题进行求解。

约束条件中除了式（10）—（12）、（19）外均为线性约束。而且式（10）—（12）与二次型相近，可以转换为SOCP的一般形式；式（19）可转换为线性约束。SOCP问题是一个非线性凸问题，可行解域为一个二阶锥 SOC（Second-Order Cone）［19］，由于 SOCP 问题是多项式时间可计算问题，在大量的实际问题中得到应用。在电力系统方面的研究也在开展，包括最优潮流［20］、网络重构［21］、配电网储能选址定容［22］、无功优化［23］等。

首先需要将约束条件处理成SOC可表示函数。引入新变量，则式（10）—（12）可转换为：

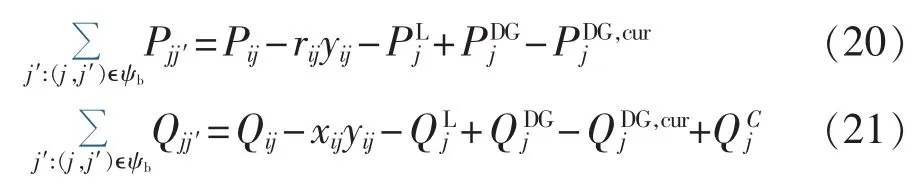
同时增加新的等式约束：

式（23）可通过松弛转换成如下 SOC 形式［24-25］：

其中，‖·‖2为欧几里德范数。 文献［24］证明了式（24）松弛的正确性，不影响规划结果。

同时，式（8）、（9）、（17）按新变量可变为：

式（27）为混合整数非线性约束，不满足SOC模型的要求［19］，对其进行线性化处理，具体如图2所示，图中vss，t为标幺值。可以看出kt在-8～8范围内变化时，用 vss，t=1.001+0.0125kt对式（27）进行拟合可以得到较好的效果，拟合之后误差平方和（SSE）为 1.183×10-5，均方根误差为 0.000 888，确定系数RSquare为0.9998。这样式（27）可表示如下：

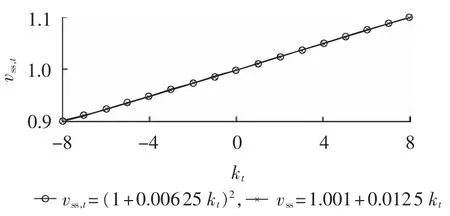
图2 式（27）曲线拟合Fig.2 Linearization for equation（27）

对于约束式（19）的处理，在此引入二进制变量bt，用以表示在t时刻OLTC触头是否动作。则式（19）可以改写成如下2个约束。

bt=0使得 kt=kt-1，即OLTC触头 kt在 t时刻不动作；bt=1限制OLTC触头kt在t时刻在合理的位置变动，即最大变动从 -8到8，或者从8到 -8。式（29）、（30）保证了OLTC触头一天的调节次数限制在6次以内。

3 算例分析

3.1 算例

采用文献［19］中算例对本文模型进行验证，算例初始网络如图3所示。IDG安装信息如表1所示。无功补偿设备安装在节点17、32，安装组数为10组，每组10 kvar，可以进相、滞相运行。OLTC为50MV·A、110±8×1.25%kV、YNd11三相双绕组变压器［26］。 IDG 类型包括风机（WTG）、光伏（PVG），采用的变压器高压侧电压、负荷、风速及光照强度数据来自实际的变电站、风电场及光伏发电厂。风机、光伏出力模型参考文献［27］。

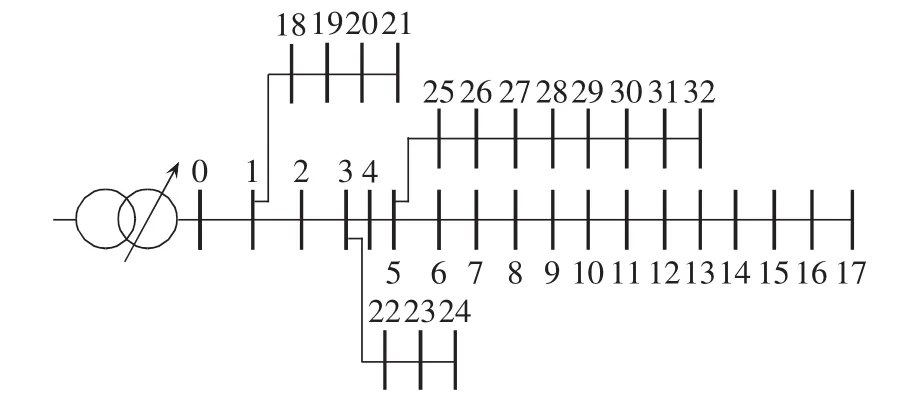
图3 IEEE 33节点算例初始网络Fig.3 Initial IEEE 33-bus network for case study

表1 IDG安装信息Table1 Installation information of IDG

功率基准值取10MV·A，电压基准值取12.66 kV。节点电压约束为0.95～1.05 p.u.，支路功率约束为5 MV·A。

选择典型场景对DG消纳进行研究，按照变压器高压侧电压、负荷、风机、光伏的历史数据选择春、夏、秋、冬4个典型场景。典型场景数据如图4所示，图中纵轴均为标幺值。为了分析不同AM策略对IDG消纳结果的影响，3种AM策略组合在算例中进行了分析，具体如下：AM1，考虑DG调度、OLTC调节、无功补偿；AM2，考虑DG调度、无功补偿；AM3，仅考虑DG调度。

本文利用 CVX［28］建模工具包及 GUROBI［29］解法器对模型进行求解。采用Core（TM）i5-4200MCPU，2.5GHz个人电脑在MATLAB 8.1平台上进行算例验证。

3.2 结果分析

表2给出了IDG年消纳结果，可以看出在AM策略AM1情况下，IDG 100%消纳。在未考虑OLTC调节的AM2情况下，IDG切除率为0.94%，IDG切除时间主要发生在春季及冬季，这是由于春季、冬季负荷较低，同时变压器高压侧电压较高所致。图5给出了冬季AM1情况下节点21所安装WTG2功率（标幺值，后同）、OLTC调节位置、节点21电压变化曲线（标幺值，后同）及负载（标幺值，后同）。由图5（a）知，WTG2安装在轻载馈线1-21末端，在负荷低谷时段，变压器高压侧电压较高，为了全部消纳WTG2发出的功率，防止电压越上限，OLTC位置调至下限-8。此时较小的负荷及较大的变压器高压侧电压，同时加上安装在重载馈线5-32、5-17末端无功补偿设备的电压支撑，保证了重载馈线末端节点17及节点32电压不越下限。图5（b）给出了节点21电压曲线。在负荷低谷时段，由于OLTC触头位置较低，使得节点21电压反而较负荷高峰时段低。

图4 算例数据Fig.4 Data for case study

表2 IDG年消纳结果Table 2 Results of annual IDG accommodation

由图6（a）可以看出冬季AM2情况下WTG2切除主要发生在 05∶00、06∶00。 该时段变压器高压侧电压达到最大，负荷较低，同时WTG2出力较大，由于AM2无OLTC调节，导致系统需进行IDG切除保证节点21负荷安全稳定供电。节点21电压在05∶00、06∶00达到上限。由图6（b）可以看出，为了防止重载馈线5-17末端节点17电压越下限，节点17安装的无功补偿设备在大多数时间都处于上限，并滞相运行。其他时刻，由于变压器高压侧电压过大，或负荷较小等原因，为了保证电压不越上限，无功补偿设备进相运行。春季IDG切除主要发生在24∶00，该时刻变压器高压侧电压较大，同时WTG出力达到最大值。

图5 冬季AM1结果Fig.5 Results of AM1 for winter

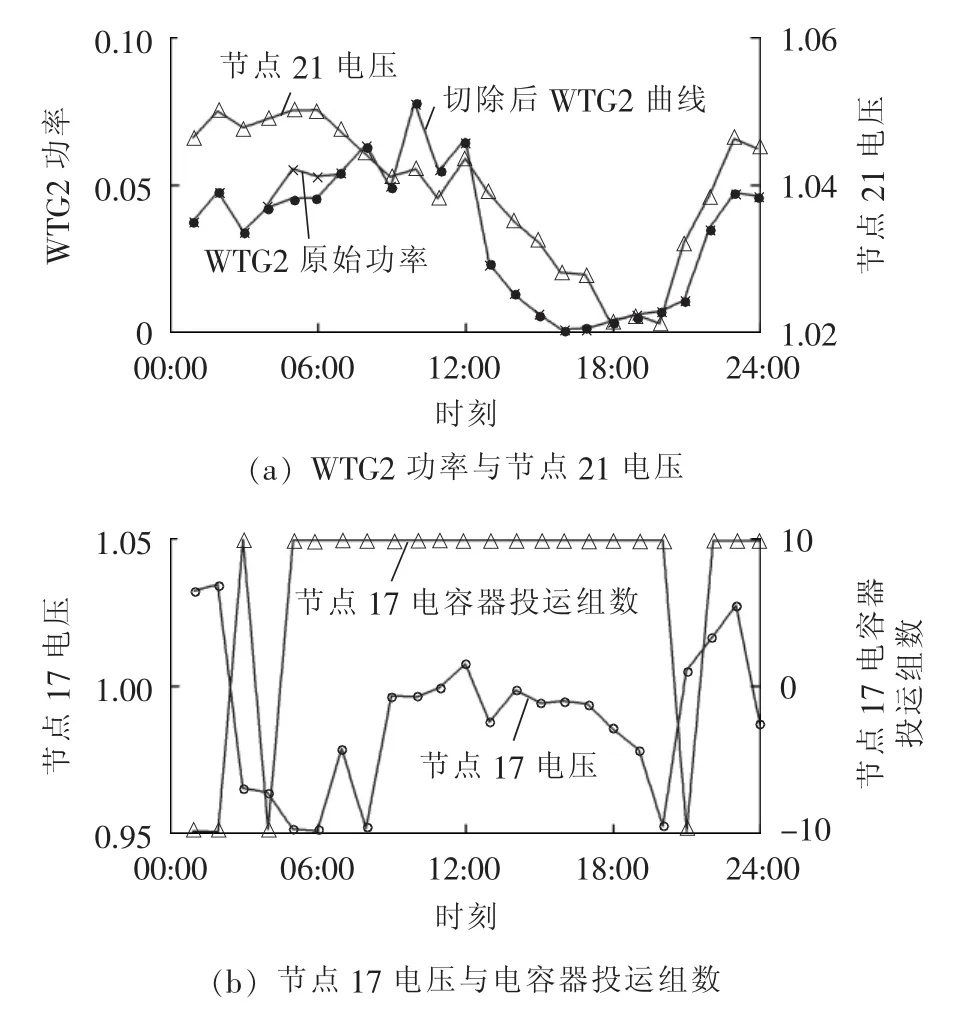
图6 冬季AM2结果Fig.6 Results of AM2 for winter

图7为夏季AM1情况下WTG2功率、OLTC调节位置、节点21电压变化曲线及负载。夏季负荷较重，对DG消纳起到了积极作用，对于所有AM策略组合，通过各种AM策略均能100%消纳分布式发电。

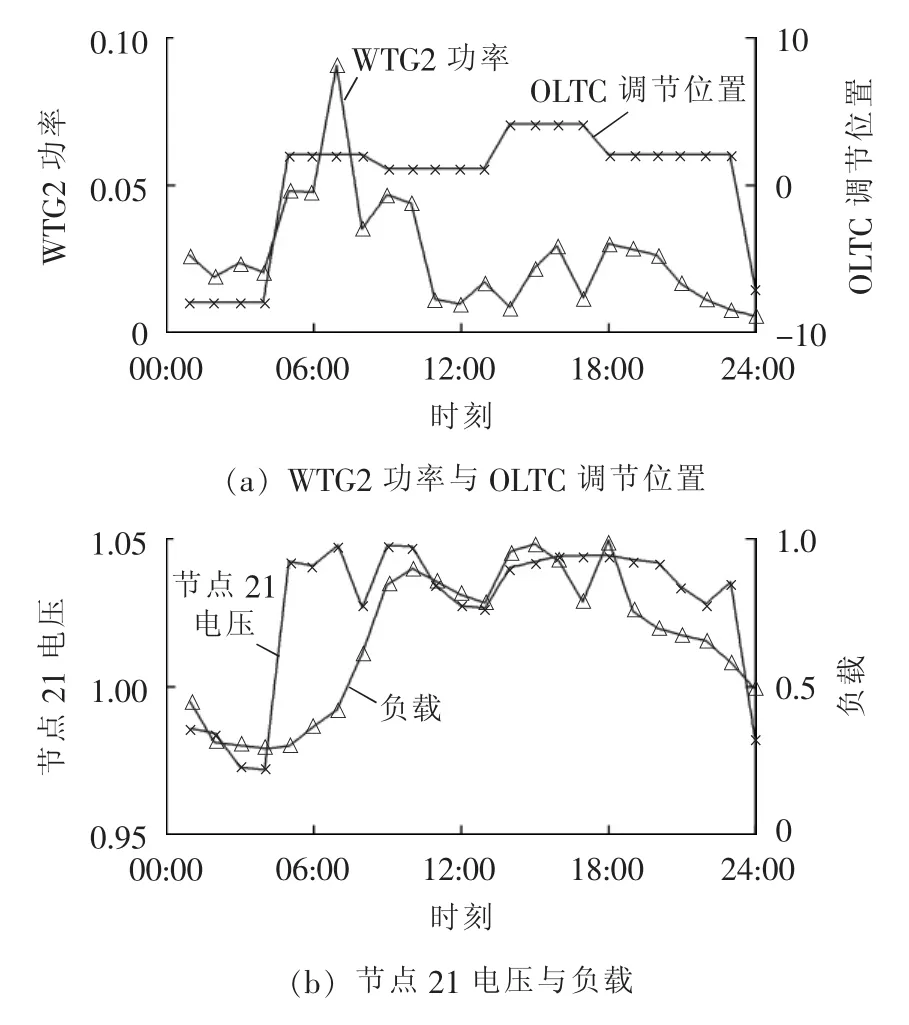
图7 夏季AM1结果Fig.7 Results of AM1 for summer

IDG的消纳量与AM策略的应用密切相关，AM策略应用越多，IDG切除量越少。在IDG规划时，建议IDG安装在重载馈线，轻载馈线IDG安装容量不能过大。

由于配电网有功损耗比重较大，运行调度人员在关注IDG消纳的同时也希望系统网络损耗得到降低。本文借助IDG消纳的SOCP模型对各种AM策略组合情况下网络损耗情况进行了分析。表3给出了不同目标函数下DG的年切除量，表4给出了不同目标函数下网络损耗情况。可以看出本文模型中若以IDG切除量最小为目标函数，则网络损耗较大；若以网络损耗最小为目标函数，则IDG切除量较大；若以IDG切除量与网络损耗之和最小为目标函数，IDG切除量及网络损耗均适中。以AM2为例，若以IDG切除量与网络损耗之和最小为目标函数，IDG切除量占总IDG发电量的5.18%，网络损耗占总负荷的6.69%。若在IDG消纳的同时想兼顾系统网络损耗，建议选择以IDG切除量与网络损耗之和最小为目标函数。由表3、表4可以看出，AM策略应用越多，DG切除量越少，网络损耗越小。

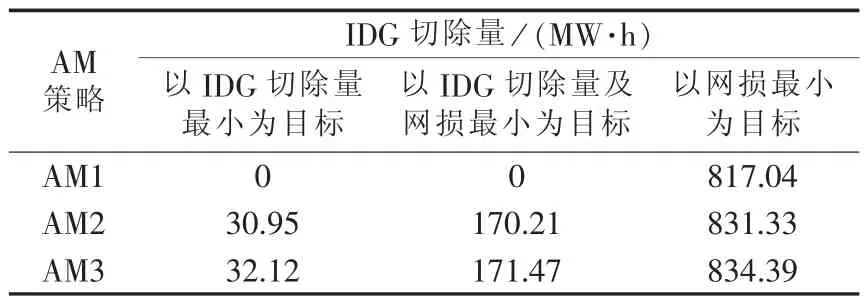
表3 不同目标函数DG年切除量Table3 Annual DG shedding for different objective functions

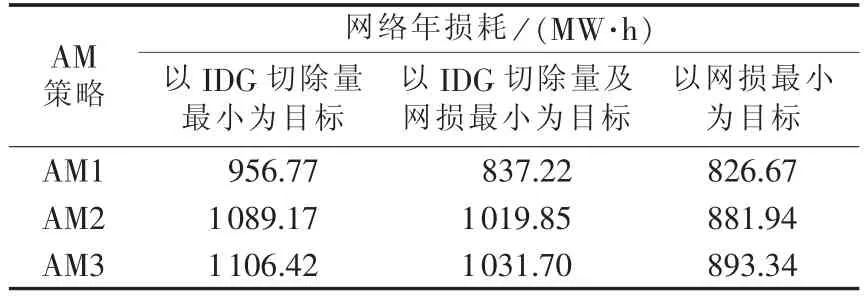
表4 不同目标函数网络年损耗Table4 Annual power loss for different objective functions

4 结语

本文分析了ADN中各种AM措施的机理。考虑IDG出力切除、OLTC分接头调节、无功补偿等多种AM措施，提出了ADN间歇性DG消纳的SOCP模型。通过CVX建模工具包及GUROBI解法器对算例进行求解，得出了算例网络的季度运行方式。同时有如下结论：IDG的消纳量与AM策略的应用密切相关，AM策略应用越多，IDG切除量越少；建议IDG安装在重载馈线，轻载馈线IDG安装容量不能过大；若配电网中同时需要考虑IDG消纳及网络损耗，AM策略应用越多，IDG切除量越少，网络损耗也越小。

［1］OCHOA L F，HARRISON G P.Minimizing energy losses：optimal accommodation and smart operation of renewable distributed generation［J］.IEEE Transactions on Power Systems，2011，26（1）：198-205.

［2］BARTON J P，INFIELD D G.Energy storage and its use with intermittent renewable energy［J］.IEEE Transactions on Energy Conversion，2004，19（2）：441-448.

［3］王孟夏，韩学山，孙宏斌.基于电热协调理论提升电网消纳间歇式能源发电能力的分析［J］. 电力自动化设备，2013，33（9）：7-12.WANG Mengxia，HAN Xueshan，SUN Hongbin. Improving intermittent energy accommodation capability of power grid based on electro-thermal coordination theory［J］.Electric Power Automation Equipment，2013，33（9）：7-12.

［4］XING Haijun，CHENG Haozhong，ZHANG Yi.Optimal coordination of intermittent distributed generation with probabilistic power flow［J］.Journal of Electrical Engineering&Technology，2015，10（6）：2211-2220.

［5］范明天，张祖平，苏傲雪，等.主动配电系统可行技术的研究［J］.中国电机工程学报，2013，33（22）：12-18.FAN Mingtian，ZHANG Zuping，SU Aoxue，et al. Enabling technologies for active distribution systems［J］.Proceedings of the CSEE，2013，33（22）：12-18.

［6］李鹏，窦鹏冲，李雨薇，等.主动配电网技术及其进展［J］.电力自动化设备，2015，35（4）：8-16.LI Peng，DOU Pengchong，LI Yuwei，et al.Application of microgrid technology in active distribution network［J］.Electric Power Automation Equipment，2015，35（4）：8-16.

［7］邢海军，程浩忠，张沈习，等.主动配电网规划研究综述［J］.电网技术，2015，39（10）：2705-2711.XING Haijun，CHENG Haozhong，ZHANG Shenxi，et al.Review of active distribution network planning ［J］.Power System Technology，2015，39（10）：2705-2711.

［8］曾博，刘念，张玉莹，等.促进间歇性分布式电源高效利用的主动配电网双层场景规划方法［J］. 电工技术学报，2013，28（9）：155-163，171.ZENG Bo，LIU Nian，ZHANG Yuying，et al.Bi-level scenario programming of active distribution network for promoting intermittent distributed generation utilization［J］.Transactions of China Electrotechnical Society，2013，28（9）：155-163，171.

［9］CHOWDHURY S，CROSSLEY P.Microgrids and active distribution networks［M］.London，UK：The Institution of Engineering and Technology，2009：2-12.

［10］MCDONALD J.Adaptive intelligent power systems：active distribution networks［J］.Energy Policy，2008，36（12）：4346-4351.

［11］AULT G，CURRIE R，MCDONALD J.Active power flow management solutions for maximising DG connection capacity［C］∥IEEE Power Engineering Society General Meeting.Montreal，Canada：IEEE，2006：1-5.

［12］CURRIE R，AULT G，FOOTE C，et al.Active power-flow management utilising operating margins for the increased connection of distributed generation［J］.IET Generation，Transmission&Distribution，2007，1（1）：197-202.

［13］张沈习，李珂，程浩忠，等.间歇性分布式电源在主动配电网中的优化配置［J］. 电力自动化设备，2015，35（11）：45-51.ZHANG Shenxi，LI Ke，CHENG Haozhong，et al. Optimal allocation of intermittent distributed generator in active distribution network［J］.Electric Power Automation Equipment，2015，35（11）：45-51.

［14］XING Haijun，CHENG Haozhong，ZHANG Yi，et al.Active distribution network expansion planning integrating dispersed energy storage systems［J］.IET Generation，Transmission&Distribution，2016，10（3）：638-644.

［15］GABASH A，LI P.Active-reactive optimal power flow in distribution networks with embedded generation and battery storage［J］.IEEE Transactions on Power Systems，2012，27（4）：2026-2035.

［16］DOLAN M J，DAVIDSON E M，KOCKAR I，et al.Reducing distributed generator curtailment through active power flow management［J］.IEEE Transactions on Smart Grid，2014，5（1）：149-157.

［17］GILL S，KOCKAR I，AULT G W.Dynamic optimal power flow for active distribution networks［J］.IEEE Transactions on Power Systems，2014，29（1）：121-131.

［18］BARAN M E，WU F F.Network reconfiguration in distribution systems for loss reduction and load balancing ［J］.IEEE Transactions on Power Delivery，1989，4（2）：1401-1407.

［19］LOBO M S，VANDENBERGHE L，BOYD S，et al.Applications of secondorder cone programming［J］.Linear Algebra and Its Applications，1998，284（1-3）：193-284.

［20］NA L，LIJUN C，LOW S H.Exact convex relaxation of OPF for radial networks using branch flow model［C］∥2012 IEEE Third International Conference in Smart Grid Communications.Tainan，China：IEEE，2012：7-12.

［21］TAYLOR J A，HOVER F S.Convex models of distribution system reconfiguration［J］.IEEE Transactions on Power Systems，2012，27（3）：1407-1413.

［22］NICK M，CHERKAOUI R，PAOLONE M.Optimal allocation of dispersed energy storage systems in active distribution networks for energy balance and grid support［J］.IEEE Transactions on Power Systems，2014，29（5）：2300-2310.

［23］刘一兵，吴文传，张伯明，等.基于混合整数二阶锥规划的三相有源配电网无功优化［J］. 电力系统自动化，2014，38（15）：58-64.LIU Yibing，WU Wenchuan，ZHANG Boming，et al.Reactive power optimization for three-phase distribution networks with distributed generators based on mixed integer second-order cone programming［J］.Automation of Electric Power Systems，2014，38（15）：58-64.

［24］FARIVAR M，CLARKE C R，LOW S H，et al.Inverter VAR control for distribution systems with renewables［C］∥2011 IEEE International Conference in Smart Grid Communications.Brussels，Belgium：IEEE，2011：457-462.

［25］XING Haijun，CHENG Haozhong，ZHANG Libo，et al.Secondorder cone model for active distribution network expansion planning［C］∥IEEE Power&Energy Society General Meeting.Denver，USA：IEEE，2015：1-5.

［26］中国国家标准化管理委员.油浸式电力变压器技术参数和要求：GB／T6451—2008［S］. 北京：中国标准出版社，2008.

［27］LIU Z，WEN F，LEDWICH G.Optimal siting and sizing of distributed generators in distribution systems considering uncertainties［J］.IEEE Transactions on Power Delivery，2011，26（4）：2541-2551.

［28］GRANT M，BOYD S.CVX：Matlab software for disciplined convex programming，version 2.0 beta［EB ／OL］. （2013-09-01）［2015-01-12］.http：∥cvxr.com／cvx.

［29］Gutobi Optimization，Inc.Gurobi optimizer reference manual，version 5.6［EB／OL］. （2013-01-01）［2015-01-12］.http：∥www.gurobi.com.