基于P-DPC的多端直流输电控制策略

江斌开，王志新 ，陆斌锋，史 莉

（1.上海交通大学 电子信息与电气工程学院，上海 200240；2.嘉兴清源电气科技有限公司，浙江 嘉兴 314031；3.上海纳杰电气成套有限公司，上海 201111）

0 引言

随着传统能源的消耗殆尽，新能源越来越受到人们的关注，而海上风电则因其诸多优点而倍受青睐。目前，大型海上风电场的远距离传输通常采用基于电压源换流器型高压直流输电（VSC-HVDC）的系统［1-2］。在双端高压直流输电的基础上，多端直流输电（MTDC）技术逐渐完善并得以应用［3-4］。 MTDC 系统至少包含3个或3个以上的变流站。由于电力传输的迅速发展，传统的双端高压直流输电已逐渐不能满足要求，MTDC越来越受到人们重视。世界上第一个多端柔性直流输电示范工程——广州南澳±160 kV多端柔性直流输电示范工程，在青澳、金牛与塑城变流站之间完成了三端变流站及系统成功试运行，促进了多端柔性直流输电技术在我国的应用。

与双端高压直流系统相比，MTDC系统除了需要考虑各个变流站自身的控制之外，还要考虑各个变流站之间的协调控制。新能源的传输、分布式电源、无源负荷都可以通过MTDC系统联系在一起，采用有效的控制策略对电压源换流器型多端直流输电（VSC-MTDC）系统的稳定运行至关重要。文献［5］提出了一种直流功率调制技术，使得MTDC系统能更灵活地向所连接的交流系统提供快速的紧急功率支持，但所连接交流系统的强度、各变流站的控制策略和直流系统电流平衡原则的选取会极大地影响直流功率调制的性能，容易造成系统不稳定。文献［6］对海上风电VSC-MTDC提出了基于直流电压的下垂控制，可以控制MTDC系统的电压稳定，但在系统发生故障时，引入频率信号，将MTDC直流电压反映的功率不平衡量转变为频率的形式，控制策略稍显复杂。文献［7］提出了采用基于直流电压偏差控制的多点直流电压控制策略，能实现定有功功率控制模式与定直流电压控制模式之间的自动转换，但要求充当主导站的变流站有足够大的后备容量以完全补偿系统功率的不平衡。文献［8］提出带电压下降特性的控制方式，可以提高整个多端系统的功率调节能力，但直流电压质量差，对于单个变流器无法实现定有功控制。

本文针对VSC-MTDC系统分别设计了基于预测-直接功率控制 P-DPC（Predictive-Direct Power Control）的本地控制器和协调控制器。P-DPC原理不复杂，控制方法简单有效，不需要传统的电压、电流控制器，充分利用了离散化数学模型，计算简单，容易数字化实现。采用该控制策略，可以实现各个变流站之间的功率协调，另一方面可以有效简化控制策略，不影响系统运行的稳定性。某个变流站发生扰动甚至退出时，由主导变流站进行功率补偿，若主导变流站达到功率出额上限，具有功率调节的变流站切换运行模式，自动承担缺额功率，保证系统稳定运行。利用MATLAB/Simulink搭建VSC-MTDC系统和控制模型，验证了所设计控制器的有效性和合理性。

1 VSC-MTDC系统建模

1.1 VSC-MTDC系统结构

MTDC变流站之间不同的连接方式可以组成不同的拓扑结构，每种拓扑可以根据具体问题进行不同的设计。图1、图2分别为VSC-MTDC系统的2种常用接线方式，即环状接线和树形状接线，本文仿真模型采用的是树形状接线。

图1 环状接线图Fig.1 Ring connection

图2 树形状接线图Fig.2 Tree connection

1.2 三相VSC数学建模

由于系统整流器与逆变器的结构相似，因此以并网逆变器为例，推导相应的数学模型。图3为三相并网逆变器［9-10］。

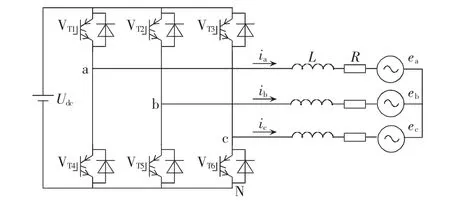
图3 三相VSC并网逆变器Fig.3 Three-phase grid-connected inverter based on VSC

如图3所示，三相并网逆变器包含6个开关，可以将开关状态定义如下：

则上述开关函数的合成矢量为：

其中，α=ej2π/3。

则三相VSC的输出电压矢量可以计算得出：

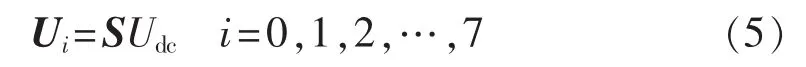
考虑6种开关状态的所有组合，可以得到总共8种电压矢量，其中U0=U7，如图4所示。

图4 三相VSC的电压矢量Fig.4 Voltage vectors of three-phase VSC

结合开关状态与直流电压，可以计算出三相VSC的输出电压，经过坐标变换得到：

如图3所示，可由基尔霍夫电流定律得到如下暂态电流方程：

假设三相电网平衡，上述暂态电流方程经过坐标变换得到如下方程：

2 VSC-MTDC的控制方法

VSC-MTDC系统由于连接了多个变流站，因此对于MTDC的控制也变得更加复杂，目前MTDC的控制系统一般由两部分组成，分别是本地控制和上层控制［8-9］。

a.本地控制接受上层控制的指令，根据不同的电压、电流指标对本地变流器进行控制。

b.上层控制采集各变流器的电流值或功率值，然后将计算出的代数和，再根据系统的控制要求或优化方案，按照一定的比例分配给各变流器（包括主变流器），作为运行参考设定值。

由于MTDC系统包含有多个变流站，各变流站间的控制作用会相互影响，因此各变流站控制器的协调控制十分重要。其中功率之间的协调配合是系统能够稳定运行的基本前提［11-12］。为防止个别变流站出现扰动或者退出运行，保证系统的稳定，各个变流站之间必须进行功率协调。根据本地控制方法的不同，各个变流站的工作模式可以分为以下3种：直流电压控制模式、功率控制模式和交流电压控制模式，其工作特性如图5所示［13-14］。图5中，Ud为直流电压，P为有功功率，Udm、Udn分别为直流电压最大、最小偏差值，Pm、Pn分别为最大、最小有功功率，Udo为额定直流电压，Pio为第i个变流站给定有功功率值，PL为负载消耗功率。

图5 各控制模式下VSC变流站的工作特性Fig.5 Working characteristics of VSC station for different control modes

2.1 变流器模型预测控制

模型预测控制技术由于其相对简单的控制原理和容易实现数字化等优点，在近年来受到广泛关注。对于变流器控制，可以理解为寻找合适的门极驱动信号去控制系统变量x（t），使其尽量接近所希望的参考变量x*（t）。模型预测控制只能在变量状态有限的情况下应用，通过全局寻优，找出最适合的控制驱动信号，将找到的最合适信号作为下一次控制的门极驱动信号。实际应用过程中，控制器计算时间与采样时间不可忽略，通过对系统变量x（t）的暂态行为分析，离散化数学方程，可以得到系统变量上一时刻与下一时刻的联系，即预测函数f。一般情况下，预测函数可以得到多种结果，如何选取最优结果就涉及到价值函数的概念。一种典型价值函数为参考值x*（t）与预测值 xi（tk+1）差的二次方，即 gi=［x*（t）-xi（tk+1）］2，除此之外还有采用参考值与预测值之差的绝对值作为价值函数。将得到的每一个预测值代入价值函数中，全局寻优对比，选择使价值函数gi最小的控制行为［15-17］。 其具体过程如下［18］：假设在 tk时刻，系统已准确控制，开关函数为 S（tk），系统变量为 x（tk）。 则tk+1时刻的系统变量 xi（tk+1）可通过预测函数 f（x（tk），S（tk））计算得出。设定以被控系统变量准确跟踪参考值为控制目标，即价值函数g的设定，则按上述预测函数可以得到价值函数最小的开关函数S（tk+1），将得到的新的开关函数应用到变流器控制上，重复上述过程。算法原理如图6所示。

本文设定被控系统变量为有功功率和无功功率，通过模型预测得出系统的有功功率与无功功率，根据价值函数直接给出变流器控制信号，即P-DPC方法。

图6 模型预测算法原理Fig.6 Principle of MPC

2.2 逆变侧控制器设计

基于P-DPC控制器设计分为如下步骤。

a.离散化所得到逆变器数学模型，即将式（8）离散化，得到如下方程：

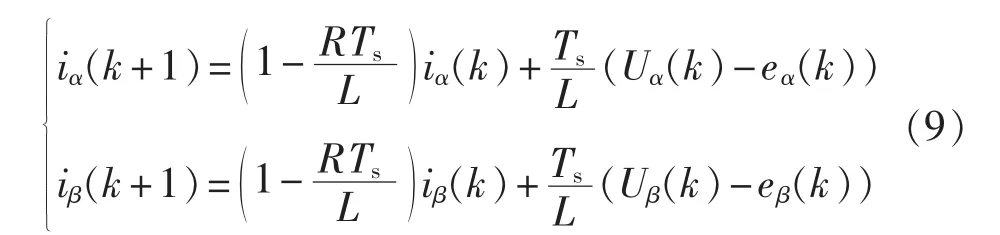
从式（9）可知，经过离散化逆变器数学模型后，可以得到下一时刻的电流与上一时刻电流之间的联系，即可以从k时刻的电流预测出（k+1）时刻的电流。经过旋转变换可得dq旋转坐标下的方程：

其中，θ为电网的空间角度；id（k+1）、iq（k+1）分别为k时刻预测出的三相并网逆变器输出电流d轴、q轴分量。

假设电网稳定，则三相电压可认定为基本不变。这样就可以通过以下方程预测得出（k+1）时刻的有功功率和无功功率。

b.选定价值函数。结合价值函数最小原则与功率平衡，采用如下价值函数：

其中，P*与Q*分别为给定的有功功率和无功功率参考值。利用价值函数式（12），通过全局寻优，可以反推出最接近期望功率的大小，从而可以得到该状态下的电压大小，再由式（6）可以得到最合适的开关状态。整个过程即为通过P-DPC给出开关矢量。

基于P-DPC控制策略的结构框图如图7所示。

2.3 整流侧控制器设计

整流侧变流器承担了稳定直流电压和提供系统功率的功能，因此，整流侧变流器必须采用定直流电压控制模式，控制直流电压和无功功率。由于与逆变侧结构相似，不难得到整流侧VSC数学模型：

图7 基于P-DPC的逆变侧变流器控制结构Fig.7 Control structure of inverter-side converter based on P-DPC

由于认为直流电压稳定，Uα、Uβ仍然可以由式（6）计算得到。离散化式（13）可以得到预测电流函数：

再经过d、q旋转变换以及数学计算，可以得到输入VSC的有功功率和无功功率，体现形式仍然可以由式（11）表示。由于整流侧变流器必须承担调节功率的功能，所以在控制器中需加入直流功率调节环节。对于价值函数的选取，整个系统必须在功率平衡下才能可靠运行，采用如下价值函数：

其中，Pdc为调节后的直流功率；Pi为除整流侧变流器外其他变流站消耗的有功功率。各Pi的大小依赖于较快速的通信系统。整个过程仍然基于P-DPC的矢量控制，控制框图如图8所示。

图8 基于P-DPC的整流侧变流器控制结构Fig.8 Control structure of rectifier-side converter based on P-DPC

3 协调控制器设计

在多端系统中若仅仅指定一个变流器采用定直流电压控制，会导致系统运行可靠性差和有功功率不能准确控制［19］，因此需要对一些变流器采用模式切换控制，当主变流器无法满足功率调节时候，具有功率调节功能的变流器能够自动承担功率缺额。本文中建立三端直流输电系统，其中VSC1为主变流器，采用定直流电压控制；VSC2引入P-DPC协调控制，工作状态能够在功率模式与直流电压模式之间切换，即具有功率调节能力；VSC3工作在功率模式，不可切换。

基于P-DPC协调控制原理如下。

（1）正常工作状态，各个变流器的预测功率通过通信系统传输到主变流器，利用式（6）与价值函数式（15），给出正常工作状态下主变流器的控制门极信号，实现P-DPC，保证各个变流器直接功率平衡；此时VSC1工作在定直流电压模式，VSC2、VSC3工作在功率模式。通常情况，系统工作在这个状态，工作状态如图9（a）所示。

图9 各状态下的VSC变流站的工作运行点Fig.9 Operating point of VSC station for different statuses

（2）VSC3功率突变，VSC1的输出功率超出其自由调节的允许范围［P1min，P1max］，超出功率部分将由直流系统内所有具有功率调节能力的VSC2来承担。此时，VSC1保持最大功率或最小功率输出，工作在定直流电压控制模式。基于P-DPC协调控制，VSC2由功率模式切换到直流电压模式，自动承担功率缺额，使整个系统重新保持功率平衡，VSC3仍然工作在功率模式。工作状态如图9（b）所示。

（3）主变流器VSC1退出运行，VSC2完全承担功率缺额，VSC2由功率模式切换到直流电压模式，VSC3仍然工作在功率模式。此时相当于普通VSCHVDC两端系统。工作状态如图9（c）所示。

图10所示为基于P-DPC的协调功率控制器。当工作在正常状态时，P1min

图10 基于P-DPC的协调功率控制器Fig.10 Power coordinating controller based on P-DPC

4 仿真结果与分析

本文用仿真软件MATLAB/Simulink对图2所示的系统进行数字仿真研究，验证模型和控制策略的有效性，仿真参数如下：VSC1、VSC2、VSC3 线电压为380 V，直流电容为4.7 mF，直流电压为750 V，线路阻抗R=0.005 Ω、L=5 mH，采样频率为20 kHz。 表1为变流器初始工作状态。讨论了系统在以下几种情况的响应过程，即：（1）正常工作状态，VSC3侧有功功率突变，VSC1输出功率在调节范围之内；（2）VSC3侧有功功率突变，VSC1输出功率超出调节范围；（3）VSC1 短时故障退出。

表1 变流器初始工作状态Table 1 Initial working statuses of VSC

图11为情况（1）下的系统响应。从图11可以看出，当处于正常工作状态时，有功功率和直流电压都很稳定，其中，直流电压与预设值一样，保持在750 V。在0.1～0.2 s时，VSC3功率产生波动，由6 kW变化到-6 kW时，主变流器VSC1自动调节功率平衡，系统运行稳定，说明基于P-DPC的控制策略是有效的。此情况下，VSC1工作在定直流电压模式，VSC2和VSC3工作在功率模式。

图12为情况（2）下的系统响应。由图12可以看出，在0.1～0.2 s时，VSC3的有功功率突变，由原来的6 kW变化到-15 kW，引起了直流系统功率不平衡，注入直流网络的功率小于其输出功率，直流电压下降，系统工作点发生变化。为检验控制器的有效性，设置VSC2初始功率为-20 kW，此时功率输出已超出主变流器VSC1的调节范围［-30 kW，30 kW］。VSC1保持最大功率30 kW输出，VSC2工作模式由功率模式自动切换到直流电压模式，调节系统功率平衡。

图11 情形（1）的系统响应Fig.11 System response in Condition 1

图12 情形（2）的系统响应Fig.12 System response in Condition 2

图13给出了情况（3）下的系统响应。0.1～0.2 s，VSC1的短时退出运行造成了直流系统功率不平衡，直流电压发生波动，VSC2由功率模式切换至直流电压模式，调节系统功率平衡，稳定直流电压。0.2 s之后，断路器重合闸，系统在0.05 s内恢复正常运行。

图13 情形（3）的系统响应Fig.13 System response in Condition 3

5 结论

本文利用变流器有限控制集模型预测控制，将预测功率应用到变流器控制中，设计了基于P-DPC的变流器本地控制器和协调控制器。该控制方法保留了预测控制的众多优点，有效避免了传统双闭环控制的PI参数整定和计算，无需线性控制器和脉宽调制，对变流器整流和逆变的控制复杂性大幅降低。同时，基于P-DPC的控制策略充分利用了离散化数学模型，计算简单，容易数字化实现。

MATLAB/Simulink仿真表明所提出的控制策略并不复杂，而且相对传统控制策略更加容易实现，控制效果好，为MTDC控制提供了一种新思路。

［1］WANG Zhixin，JIANG Chuanwen，AI Qian，et al.The key technology of offshore wind farm and its new development in China ［J］.Renewable and Sustainable Energy Reviews，2009，13（1）：216-222.

［2］WU Jie，WANG Zhixin，XU Lie，et al.Key technologies of VSCHVDC and its application on offshore wind farm in China［J］.Renewable and Sustainable Energy Reviews，2014，36（8）：247-255.

［3］张文亮，汤涌，曾南超.多端高压直流输电技术及应用前景［J］.电网技术，2010，34（9）：1-6.ZHANG Wenliang，TANG Yong，ZENG Nanchao.Multi-terminal HVDC transmission technologies and its application prospects in China［J］.Power System Technology，2010，34（9）：1-6.

［4］汤广福，罗湘，魏晓光.多端直流输电与直流电网技术［J］.中国电机工程学报，2013，33（10）：8-17.TANG Guangfu，LUO Xiang，WEI Xiaoguang.Multi-terminal HVDC and DC-grid technology ［J］.Proceedings of the CSEE，2013，33（10）：8-17.

［5］袁旭峰，文劲宇，程时杰.多端直流输电系统中的直流功率调制技术［J］.电网技术，2007，31（14）：57-61.YUAN Xufeng，WEN Jinyu，CHENG Shijie.DC power modulation in multi-terminal HVDC transmission system［J］.Power System Technology，2007，31（14）：57-61.

［6］王伟，石新春，付超.海上VSC-MTDC输电系统协调控制策略［J］.华北电力大学学报，2013（5）：42-47.WANG Wei，SHIXinchun，FU Chao.Coordinated controlof MTDC transmission system for offshore wind farms［J］.Journal of North China Electric Power University，2013（5）：42-47.

［7］陈海荣，徐政.适用于VSC-MTDC系统的直流电压控制策略［J］.电力系统自动化，2006，30（19）：28-33.CHEN Hairong，XU Zheng.Suitable for VSC-MTDC system DC voltage control strategy［J］.Automation of Electric Power Systems，2006，30（19）：28-33.

［8］陈海荣.基于VSC的多端直流输电系统的控制策略研究［J］.电力建设，2011（8）：58-63.CHEN Hairong.Control strategy of VSC based multi-terminal HVDC transmission system［J］.Electric Power Construction，2011（8）：58-63.

［9］王国强，王志新，张华强，等.基于DPC的海上风场VSC-HVDC变流器控制策略［J］.电力自动化设备，2011，31（7）：115-119.WANG Guoqiang，WANG Zhixin，ZHANG Huaqiang，et al.DPC-based control strategy of VSC-HVDC converter for offshore wind farm［J］.Electric Power Automation Equipment，2011，31（7）：115-119.

［10］张明兴.基于VSC的多端直流输电系统的运行控制研究［D］.成都：西南交通大学，2012.ZHANG Mingxing.Research of operation and control of the VSC-MTDC［D］.Chengdu：Southwest Jiaotong University，2012.

［11］付媛，王毅，张祥宇，等.多端电压源型直流系统的功率协调控制技术［J］.电力自动化设备，2014，34（9）：130-136.FU Yuan，WANG Yi，ZHANG Xiangyu，et al.Coordinated power control of VSC-MTDC system ［J］.Electric Power Automation Equipment，2014，34（9）：130-136.

［12］CHAUDHURI N R，MAJUMDER R，CHAUDHURI B，et al.Stability analysis of VSC MTDC grids connected to multimachine AC systems［J］.IEEE Transactions on Power Delivery，2011，26（4）：2774-2784.

［13］孙文博.多端柔性直流输电系统及控制策略研究［D］.北京：华北电力大学，2012.SUN Wenbo.Research on control strategy of VSC-MTDC［D］.Beijing：North China Electric Power University，2012.

［14］陈谦，唐国庆，潘诗锋.采用多点直流电压控制方式的VSC多端直流输电系统［J］.电力自动化设备，2004，24（5）：10-15.CHEN Qian，TANG Guoqing，PAN Shifeng.VSC-MTDC using multi-terminal DC voltage control scheme ［J］.Electric Power Automation Equipment，2004，24（5）：10-15.

［15］RODRIGUEZ J，PONTT J，CORREA P，et al.Predictive power control of an AC/DC/AC converter［C］//Industry Applications Conference，2005.Fourtieth IAS Annual Meeting.New Orleans，USA：IEEE，2005：934-939.

［16］陈强，任浩翰，杨志超，等.三相并网逆变器改进型直接功率预测控制［J］.电力自动化设备，2014，34（12）：100-105.CHEN Qiang，REN Haohan，YANG Zhichao，etal.Improved predictive direct power control of three-phase grid-connected converter［J］.Electric Power Automation Equipment，2014，34（12）：100-105.

［17］杨勇，赵方平，阮毅，等.三相并网逆变器模型电流预测控制技术［J］.电工技术学报，2011，26（6）：153-159.YANG Yong，ZHAO Fangping，RUAN Yi，et al.Model current predictive control for three-phase grid-connected inverters［J］.Transactions of China Electrotechnical Society，2011，26 （6）：153-159.

［18］沈坤，章兢，王坚.一种多步预测的变流器有限控制集模型预测控制算法［J］.中国电机工程学报，2012，32（33）：37-44.SHEN Kun，ZHANG Jing，WANG Jian.A modelpredictive control scheme of multi-step prediction finite control set for converters［J］.Proceedings of the CSEE，2012，32（33）：37-44.