微电网弱约束容性等效输出阻抗逆变器控制方法

曹一家 ，郑玉芳 ，于晶荣 ，段娟凤 ，章文远

（1.湖南大学 电气与信息工程学院，湖南 长沙 410082；2.中南大学 信息科学与工程学院，湖南 长沙 410083）

0 引言

近年来，分布式发电作为优化能源结构和实现节能减排的关键技术之一，受到了世界各国的广泛关注。然而，高渗透率的分布式电源，特别是光伏、风电等具有随机性和间歇性特点的分布式电源，大量接入住宅家庭、办公楼宇等配电网末端时，会造成配电网和分布式电源自身稳定性和可靠性等方面的一系列严重问题。

微电网技术能够实现分布式电源与大电网的协调和互为支撑，是发挥分布式发电系统技术优势的最有效方式。由于电网络承载更多的是阻感性负载，目前，大多数文献针对阻性和感性逆变器控制策略进行研究，并取得了一定的成果。采用虚拟阻抗法［1-6］或者基于电感电流反馈方式的阻抗控制方法［7］，能够保证逆变器在工频附近的输出阻抗特性。但是，当微电网受到大量的非线性阻感性负荷冲击时，阻性或感性逆变电源会引起逆变器输出电压的波动，不利于微电网电压的稳定。

为了解决这一问题，进一步提出将逆变器等效输出阻抗设计成容性，使其呈无功补偿器的倾斜特性，改善微网的电压偏移［8-12］。 在文献［11］中，为了使逆变器等效输出阻抗为容性，设计了复杂的控制器且忽略了滤波电容对等效阻抗的影响。文献［9］中，采用单阻抗环控制，但是逆变器等效输出阻抗在低频时近似为虚拟电容，高频时近似为滤波电容，并不能在一定带宽下保持逆变器固定的容性特性。

本文针对文献［9，11］中存在的问题，在虚拟阻抗控制策略研究的基础上，提出了一种考虑逆变器输出电路、采样点选取和控制器等影响阻抗控制的软硬件关键环节的容性逆变器设计方法。该方法可有效弱化目前容性逆变器设计的约束条件，所设计的容性逆变器能有效改善微电网电压的稳定。

1 传统的逆变器输出阻抗双环控制

图1为微网逆变电源并联系统等效原理图。U1、U2和Uo分别为逆变电源1的输出电压、逆变电源2的输出电压和交流母线电压；δ1、δ2和 δo分别为逆变电源1输出电压相位、逆变电源2输出电压相位和公共点电压的相位；设逆变电源的等效输出阻抗及其相位分别为 Zi（i=1，2）和 θi（i=1，2）。

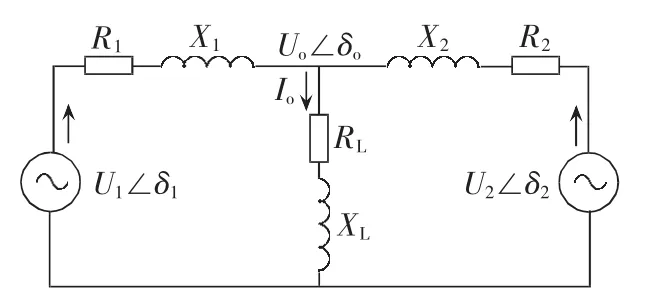
图1 微源并联系统简化原理图Fig.1 Simplified schematic diagram of system with parallel micro-sources

输出功率［7，13-14］表达式为：

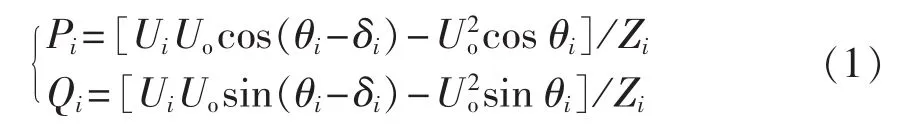
下垂控制方程如表1所示，其中mi、ni为下垂系数，ω*、U*分别为参考电压频率和参考电压幅值。

表1 下垂控制方程Table 1 Droop control equations

感性逆变器与容性逆变器具有相反的下垂曲线特性，即当微网负荷功率需求急剧增加时，感性逆变器输出电压会出现暂降现象，而容性逆变器恰恰相反。容性逆变器在微网中有助于平衡无功，从而改善微网电压的稳定［7］。

逆变器双环控制原理图如图2所示。图中，uref为逆变器输出参考电压；Gu为电压环控制器；Gi为电流环控制器；Gv为虚拟阻抗控制器；kpwm为逆变器等效环节（kpwm≈1）；ui为逆变桥输出电压；L、r分别为逆变侧电感及其等效电阻；iL为逆变侧电流；iC为流过滤波电容的电流；io为网侧输出电流；C为滤波电容；uo为电容两端的电压。

图2 逆变器双环控制原理图Fig.2 Block diagram of inverter dual-loop control

令 uref=0，逆变器等效输出阻抗［4，7］表达式为：

其中，B=kpwmGu（s）Gi（s）；A1=r+kpwmGi（s）；A0=kpwm×Gu（s）Gi（s）+1。

如忽略滤波电容项，式（2）可以改写成：

在输出电流支路添加阻抗控制器Gv且在合理情况下忽略L或忽略r时，该方法能使逆变器等效输出阻抗为纯阻性或纯感性［4，7，15］，但是其 难以实现容性逆变器的设计。为此，文献［16］提出在电流反馈支路设置阻抗控制器，并引入2个局部控制器使逆变器等效输出阻抗为容性，但所使用的局部控制器较为复杂，不利于实际工程应用。因此，本文提出一种控制器简易实现、弱化约束条件的容性逆变器设计方法。

2 容性逆变器控制器建模

2.1 基于LCCL滤波器的逆变微源

采用不同的滤波器和不同的反馈电流，电流控制系统抑制电流谐波的效果就不同。LCL三阶滤波器抑制高频的能力比L滤波器强，但其电流控制策略较之复杂。电流反馈方式不同，电流控制系统的复杂程度不同，设计合理的电流内环控制器，可使电流环稳定。在文献［17］中，将LCL滤波器的滤波电容C裂解成等效的2个电容，并比较不同电流反馈方式下电流控制系统的差异，最终得出以裂解点电流为反馈，可以简化电流控制系统的阶次以及减小系统稳态误差和电流谐波畸变。图3所示为单个微源的系统结构。图中，C1和C2为LCL滤波器的滤波电容裂解成的 2 个等效的电容，且 C1=βC，C2=（1-β）C。图中L2、r2分别为网侧滤波电感及其等效电阻，Lg、rg分别为线路感抗和阻抗，if为2个裂解滤波电容C1和C2间的电流，um为控制电压信号，ug为PCC电压。

图3 系统的拓扑结构Fig.3 System topology of a micro-source

设 L′=L+L2+Lg，r′=r+r2+rg，α=L /L′=r/r′，β=1-α，则反馈电流到逆变器桥输出电压传递函数［17］为：

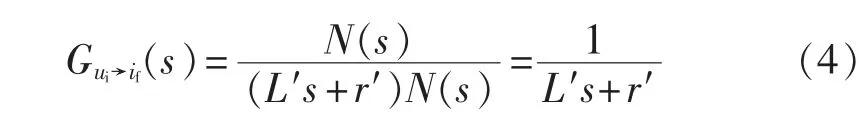
其中，N（s）=α（1-α）L′Cs2+α（r2+rg）Cs+1。

采用LCCL滤波器，实际开关纹波电流是通过三阶滤波器进行抑制的，而以裂解点电流为反馈电流，可使电流控制系统由三阶降为一阶，类似于L滤波器的传递函数，降低控制的复杂度。

2.2 容性逆变器双环控制建模

本文所提容性逆变器控制模型如图4所示，采取电压阻抗双环控制结构。在if的反馈支路，引入虚拟阻抗控制器Gv，通过电压电流控制得出PWM调制波，从而控制H桥开关管的通断得到ui，ui经LCCL滤波器滤波获得逆变器输出电压。从LCL滤波器的配置看，逆变侧滤波电感L相对于网侧滤波电感Lg的值很大，故可选取电容两端的电压为输出电压。

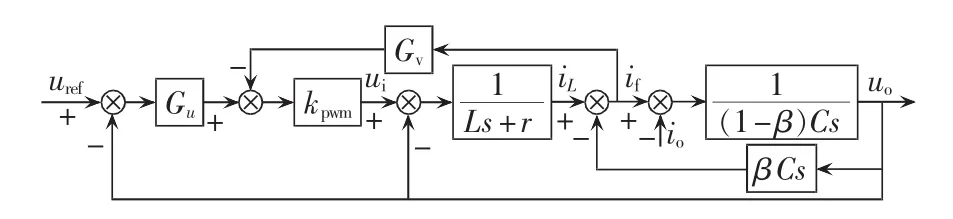
图4 容性逆变器双环控制框图Fig.4 Block diagram of dual-loop control for capacitive inverter

由图4可得系统输出电压的传递函数为：

其中，X=Gu（s）kpwm，Y=Gv（s）kpwm。

当逆变器输出参考电压为零时，逆变器等效输出阻抗为：

从式（6）可以看出，结合阻抗控制，输出阻抗由于存在由裂解电容产生的一个可控自由度β的缘故，可以巧妙地设计阻抗控制器及电压控制器，使得逆变器输出阻抗等效成容性，即令 Gv（s）= （X+1）÷（kpwmβCs），则 Zo（s）=1/（Cs）。

与传统双环控制相比，所提出的方法之所以能够使逆变器等效输出阻抗为容性，关键点在于滤波电容的裂解及选取裂解电流反馈为逆变器等效输出阻抗提供一个可控自由度。

2.3 双环控制系统分析

由2.2节可知，内外环控制器Gv和Gu存在耦合关系，设Gu为比例控制器，Gv相当于积分控制器。由图4可得系统的开环传递函数为：

图5为系统典型奈奎斯特图，其中，A=（β-1）÷（1-β），系统的稳定性主要取决于Gu控制器和β的取值。当Gu＞A时，系统开环传递函数的奈奎斯特轨迹沿逆时针方向没有包围实轴上的点（-1，j0），且由式（7）可知，系统开环传递函数在S复平面的虚轴上既无零点也无极点。由奈奎斯特稳定判据得，当Gu＞A时系统稳定。

图5 系统典型奈奎斯特图Fig.5 Typical Nyquist plot of system

3 仿真结果及分析

本文采用MATLAB/Simulink仿真平台搭建单相逆变微源仿真模型，L=0.585 mH，C=1000 μF，β=0.1，Gu=-0.9。逆变器的额定视在功率为6.5 kV·A，逆变电源的直流母线电压为350 V（由直流稳压电源提供），额定输出电压为230 V，额定输出电流峰值为40 A，系统频率为50 Hz，开关频率为10 kHz。负载阻抗为 RL=30 Ω 和 ZL=（20＋j22）Ω。

本文采用文献［8］中所提出的鲁棒下垂控制，取Ke=10，ni=6.3 × 10-4，mi=3.4 × 10-5，U*=230 V，ω*=100πrad/s。

本文共搭建2组仿真实验模型。第1组实验：同等硬件条件下，不同等效输出阻抗逆变微源独立运行，负载阻抗为RL，运行时长为5 s，2 s时并联负载 ZL，4 s时断开 ZL。 实验结果如图6所示，（a）—（d）各图中从上到下分别对应容性逆变器、阻性逆变器和感性逆变器。从图6可以看出，当并入或者切断额外负荷ZL时，容性、阻性和感性逆变器均能快速地响应并达到稳定状态，且容性逆变器响应速度最快。对比各逆变器的输出电压的有效值，在系统负荷变动下，感性和阻性逆变器的输出电压有效值波动接近20 V，而容性逆变器只波动10 V左右。可见，相比阻性和感性逆变器，在系统负荷变动下，容性逆变器的电压波动更小，响应速度更快。

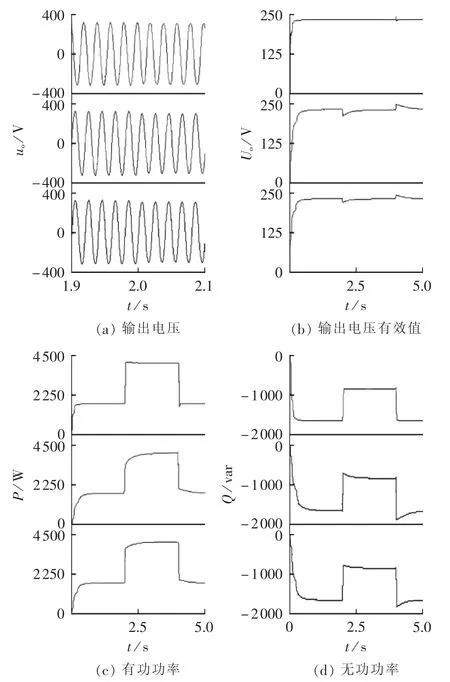
图6 第1组仿真波形Fig.6 Simulative waveforms of test 1

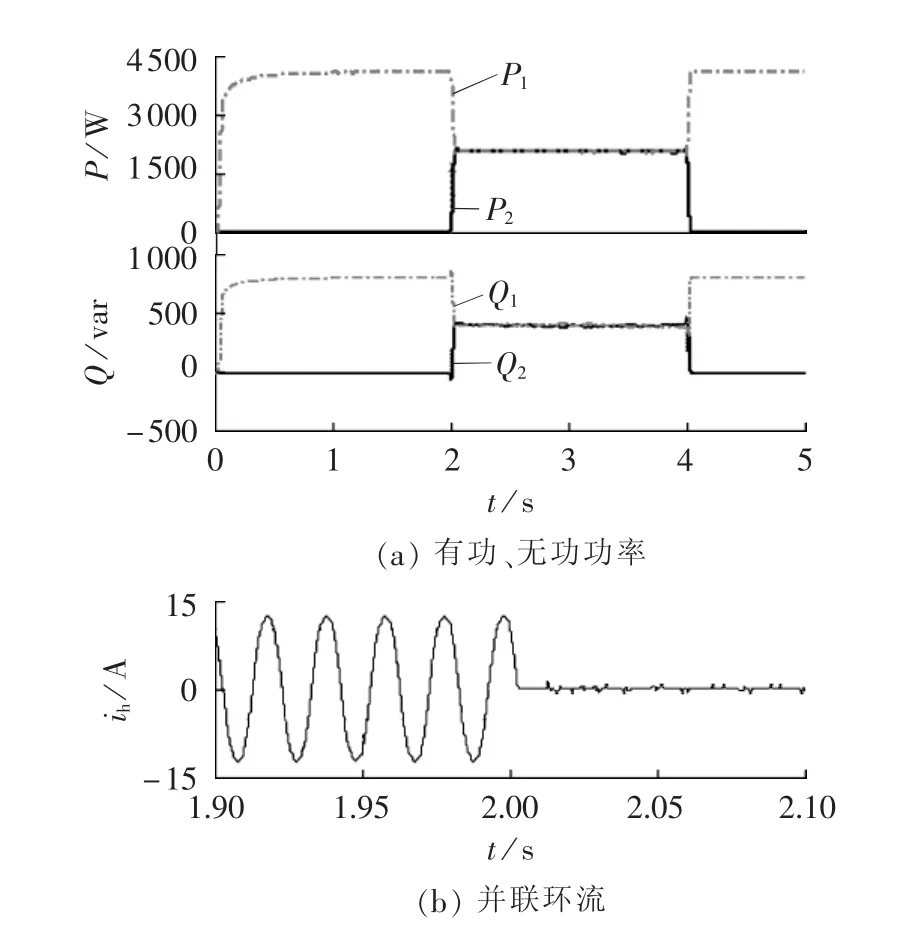
图7 2台容性逆变器并联仿真波形Fig.7 Simulative waveforms of two parallel capacitive inverters

第2组实验：2台逆变器并联运行，负载阻抗为RL和ZL并联，并在第2台逆变器增加线路阻抗ZLine=（0.2＋j0.02）Ω，运行时长为 5 s，最初第 1 台逆变器独立运行，2 s时并联第2台逆变器，4 s时将其切断。2 台逆变器的并联环流 ih=（i1-i2）/2（i1和 i2为各逆变器的输出电流）。图7和图8给出了分别用2台容性逆变器和2台感性逆变器并联的仿真结果。从仿真结果可以看出，对比感性逆变器并联系统，容性逆变器并联系统具有更好的功率均分特性和更快的动态响应速度。

图8 2台感性逆变器并联仿真波形Fig.8 Simulative waveforms of two parallel inductive inverters

4 结语

本文提出一种综合滤波电路配置、采样电流选取以及阻抗控制器设计的容性逆变器的控制策略。该方法能为逆变器输出阻抗模型提供一个可控自由度，弱化约束条件，使得逆变器输出阻抗在一定频带下保持容性特性。

设计的2组仿真实验证明，在同等硬件条件下，对比感性和阻性逆变器，本文所提出的容性逆变器能有效改善微电网电压质量，具备较快的响应速度和较强的电压稳定能力。

［1］GUERRERO J M，VICUNNA L G，MATAS J，et al.Output impedance design of parallel-connected UPS inverters with wireless load-sharing control［J］.IEEE Transactionson Industrial Electronics，2005，52（4）：1126-1135.

［2］GUERRERO J M，MATAS J，VICUNNA L G，et al.Decentralized control for parallel operation of distributed generation inverters using resistive output impedance［J］.IEEE Transactions on Industrial Electronics，2007，54（2）：994-1004.

［3］HE J，LI Y W.Analysis，design，and implementation of virtual impedance for power electronics interfaced distributed generation［J］.IEEE Transactions on Industrial Application，2011，47（6）：2525-2538.

［4］关雅娟，邬伟扬，郭小强.微电网中三相逆变器孤岛运行控制技术［J］.中国电机工程学报，2011，31（33）：52-60.GUAN Yajuan，WU Weiyang，GUO Xiaoqiang.Control strategy for three-phase invertersdominated microgrid in autonomous operation［J］.Proceedings of the CSEE，2011，31（33）：52-60.

［5］张宸宇，梅军，郑建勇，等.一种适用于低压微电网的改进型下垂控制器［J］.电力自动化设备，2015，35（4）：53-59.ZHANG Chenyu，MEIJun，ZHENG Jianyong，etal.Improved droop controller for low-voltage micro-grid ［J］.Electric Power Automation Equipment，2015，35（4）：53-59.

［6］胡雯，孙云莲.逆变型微电源孤岛模式下的控制策略［J］.电力自动化设备，2014，34（7）：107-113.HU Wen，SUN Yunlian.Control strategy of inverter-based microsources in island mode［J］.Electric Power Automation Equipment，2014，34（7）：107-113.

［7］吕志鹏，罗安.不同容量微源逆变器并联功率鲁棒性控制［J］.中国电机工程学报，2012，32（12）：35-42.LU¨Zhipeng，LUO An.Robust power control of paralleled microsource inverters with different power ratings［J］.Proceedings of the CSEE，2012，32（12）：35-42.

［8］ZHONG Q C，ZENG Y.Can the output impedance of an inverter be designed capacitive？ ［C］//37th Annual Conference on IEEE Industrial Electronics Society.Melbourne，Australia：IEEE，2011：1220-1225.

［9］ZHONG Q C，ZENG Y.Control of inverters via a virtual capacitor to achieve capacitive output impedance［J］.IEEE Transactions on Power Electronics，2014，29（10）：5568-5578.

［10］汪英，张庆海.容性等效输出阻抗的逆变器并联控制研究［J］.电源技术，2014，38（11）：2188-2191.WANG Ying，ZHANG Qinghai.Research of parallel control for inverters with capacitive equivalent output impedance［J］.Chinese Journal of Power Sources，2014，38（11）：2188-2191.

［11］陈燕东，罗安，王文，等.阻容性逆变器及其并联功率精确分配方法［C］//第七届中国高校电力电子与电力传动学会年会（SPEED）.上海，中国：［出版者不详］，2013：150-156.CHEN Yandong，LUO An，WANG Wen，et al.Rapid reactive power control method for parallel inverters using resistive-capacitive output impedance［C］//7th Symposium on Power Electronics&Electrical Drives.Shanghai，China：［s.n.］，2013：150-156.

［12］SAVAGHEBI M，JALILIAN A，VASQUEZ J C，et al.Secondary control scheme for voltage unbalance compensation in an islanded droop-controlled microgrid［J］.IEEE Transactions on Smart Grid，2012，3（2）：797-807.

［13］YAO W，CHEN M，MATAS J，et al.Design and analysis of the droop control method fox parallel inverters considering the impact of the complex impedance on the power sharing［J］.IEEE Transactions on Industrial Electronics，2011，58（2）：576-587.

［14］王成山，高菲，李鹏，等.低压微网控制策略研究［J］.中国电机工程学报，2012，32（25）：2-8.WANG Chengshan，GAO Fei，LI Peng，et al.Control strategy research on low voltage microgrid［J］.Proceedings of the CSEE，2012，32（25）：2-8.

［15］陈燕东，罗安，龙际根，等.阻性逆变器并联环流分析及鲁棒性下垂多环控制［J］.中国电机工程学报，2013，33（18）：18-29.CHEN Yandong，LUO An，LONG Jigen，et al.Circulation current analysis and robust droop multiple loop control for parallel inverters using resistive output impedance［J］.Proceedings of the CSEE，2013，33（18）：18-29.

［16］吕志鹏，刘海涛，苏剑，等.可改善微网电压调整的容性等效输出阻抗逆变器［J］.中国电机工程学报，2013，33（9）：1-8.LU¨Zhipeng，LIU Haitao，SU Jian，et al.Micro-source inverters with capacitive equivalent output impedance for improving micro-grid voltages［J］.Proceedings of the CSEE，2013，33（9）：1-8.

［17］SHEN G Q，XU D H，CAO L P，et al.An improved control strategy for grid-connected voltage source inverter with an LCL filter［J］.IEEE Transactions on Power Electronics，2008，23（4）：1899-1906.