碳纳米管对天然橡胶的补强机理研究*

朱常才，杨 琨，张亭亭，张萍，赵树高

(青岛科技大学 橡塑材料与工程教育部重点实验室/山东省橡塑材料与工程重点实验室,山东 青岛 266042)

从碳纳米管(CNT)被发现以来[1]，由于其具有优良的力学性能、高长径比、低密度、极好的耐热性、导热性等，使CNT作为补强材料具有巨大的应用优势[2-6]。研究具有不同拓扑结构的纳米填料的力学性能所用的模型不同，对CNT等纤维状补强填料有多种理论模型描述其力学性能，如剪切迟滞模型[7]、Eshelby模型[8]、Tandon-Weng模型[9]、Halpin-Tsai模型[10]等，由于Halpin-Tsai模型能用于研究纤维在高聚物基体中呈三维取向复合材料的力学性能，故应用广泛，可以根据该模型的理论计算值和实验值进行比较，探究纤维在基体中的状态，从而为补强机理的研究提供一定的理论支持。

目前对CNT补强橡胶的补强机理并不清楚。基于此，本文采用机械共混法制备了CNT/天然橡胶(NR)复合材料，并对其力学性能及填料微观状态进行了表征。在此基础上，采用Halpin-Tsai模型分别对取向纤维补强、无规纤维补强这两种主要情况下复合材料的力学强度进行了理论计算，并与实验数据进行比较，从而确定了机械共混法获得的CNT/NR复合材料中CNT对NR的补强机理及CNT长径比对补强性能的影响。

1 实验部分

1.1 原料

NR：SMR 10，马来西亚进口；多壁碳纳米管：管外直径为10～30 nm，内直径为510 nm，密度为0.14 g/cm3，表面—COOH的质量分数为1.55%，中国科学院成都有机化学有限公司；甲苯：莱阳经济技术开发区精细化工厂；ZnO、SA、NS、S均为市售。

1.2 仪器设备

电子天平：TA2003，上海天平仪器厂；HAAKE转矩流变仪：Thermo Scientific公司；开炼机：BL-6175BL，宝轮精密检测仪器公司；无转子硫化仪：MDR2000，美国ALPHA公司；硫化仪：HS-100T-RTMO，深圳佳鑫电子设备科技有限公司；橡胶电子拉伸机：Z005，德国Zwick公司；场发射扫描电子显微镜：JSM-7500，日本株式会社；透射电子显微镜：EM-ARM200F，日本株式会社。

1.3 胶料配方

橡胶的配方如表1所示，其中CNT的用量分别为0、3、6、9、12 phr。

表1 CNT/NR复合材料的实验配方

1.4 复合材料的制备

胶料的制备采用HAAKE转矩流变仪，混炼转速为50 r/min，初始温度为60 ℃，混合10 min后加入硫黄，下片，得到混炼胶。胶料硫化采用GB/T 16584—1996及ISO 6502—1991标准，在150 ℃、15 MPa下硫化。

1.5 复合材料的表征

硫化特性测试采用MDR2000型无转子硫化仪，温度为150 ℃，下模腔摆动角度为±1°；力学性能测试在Z005型橡胶电子拉力机上按照GB/T 528—1998标准进行，拉伸速率为500 mm/min；用JSM-7500型场发射扫描电子显微镜及EM-ARM200F型透射电子显微镜表征CNT在复合材料中的形貌和分散；结合橡胶质量分数的测量采用甲苯作为溶剂。

2 结果与讨论

2.1 CNT对NR补强性能研究

表2为CNT含量不同时复合材料的力学性能测试结果。从表2可知，随着CNT含量的增加，在断裂伸长率不变的情况下，复合材料的定伸模量、撕裂强度都有较大的提高，说明CNT是一种优异的补强材料，即使在较低的含量时也具有优异的补强性能。

表2 不同CNT用量的CNT/NR复合材料的物理机械性能

1) CNT/NR-0、3、6、9、12表示NR中CNT用量为0、3、6、9、12 phr。

填料的补强效果与复合材料中结合橡胶的含量有直接的关系，结合橡胶含量反映了填料与橡胶基体的相互作用，结合橡胶含量越高，相互作用越强。表3为CNT含量不同时复合材料中结合橡胶的含量。从表3可知，随着CNT含量的增加，结合橡胶的含量急剧增加。结合橡胶为CNT和NR相互作用所形成，对NR具有补强作用，结合橡胶含量增加，补强效果增强。

表3 CNT/NR复合材料中结合胶的含量

图1给出了CNT/NR-9不同状态下的扫描电镜图片。从图1可以看出，对于处于原始状态的CNT/NR复合材料来说，拉断时CNT并未明显被拔出，且表面存在包覆胶，拉伸时未出现CNT拔出，进一步说明CNT和NR具有较强的相互作用。

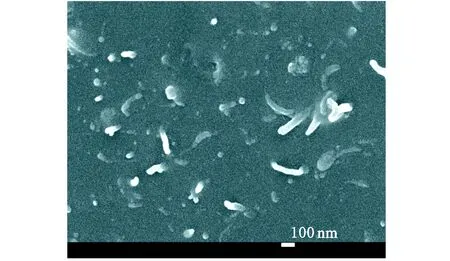
(a) 静态

(b) 拉伸状态图1 复合材料(CNT/NR-9)在静态和拉伸状态下的扫描电镜照片

CNT的补强效果还与其分散情况有关。图2为CNT/NR复合材料的透射电镜图片。从图2能够明显看出，CNT在复合材料中能够均匀分散，当CNT用量较少时(CNT/NR-3)，CNT为独立分布状态，之间无相互作用。但是当CNT用量为9 phr时，复合材料中的CNT已经不再是独立分布状态，它们之间产生了一定的相互作用，Deng等[11]已经证明当NR中CNT含量较多时，CNT会在复合材料中形成三维网络结构。从图1(b)可以看出，CNT及其三维网络结构作为骨架材料承担了拉伸过程中的应力，从而提高其拉伸模量，同时在拉伸过程中材料内部产生缺陷。并且结合图1及前期工作[12]可以知道，由于三维网络是由CNT之间的物理缠结产生，当形变较大时，三维网络会被破坏。

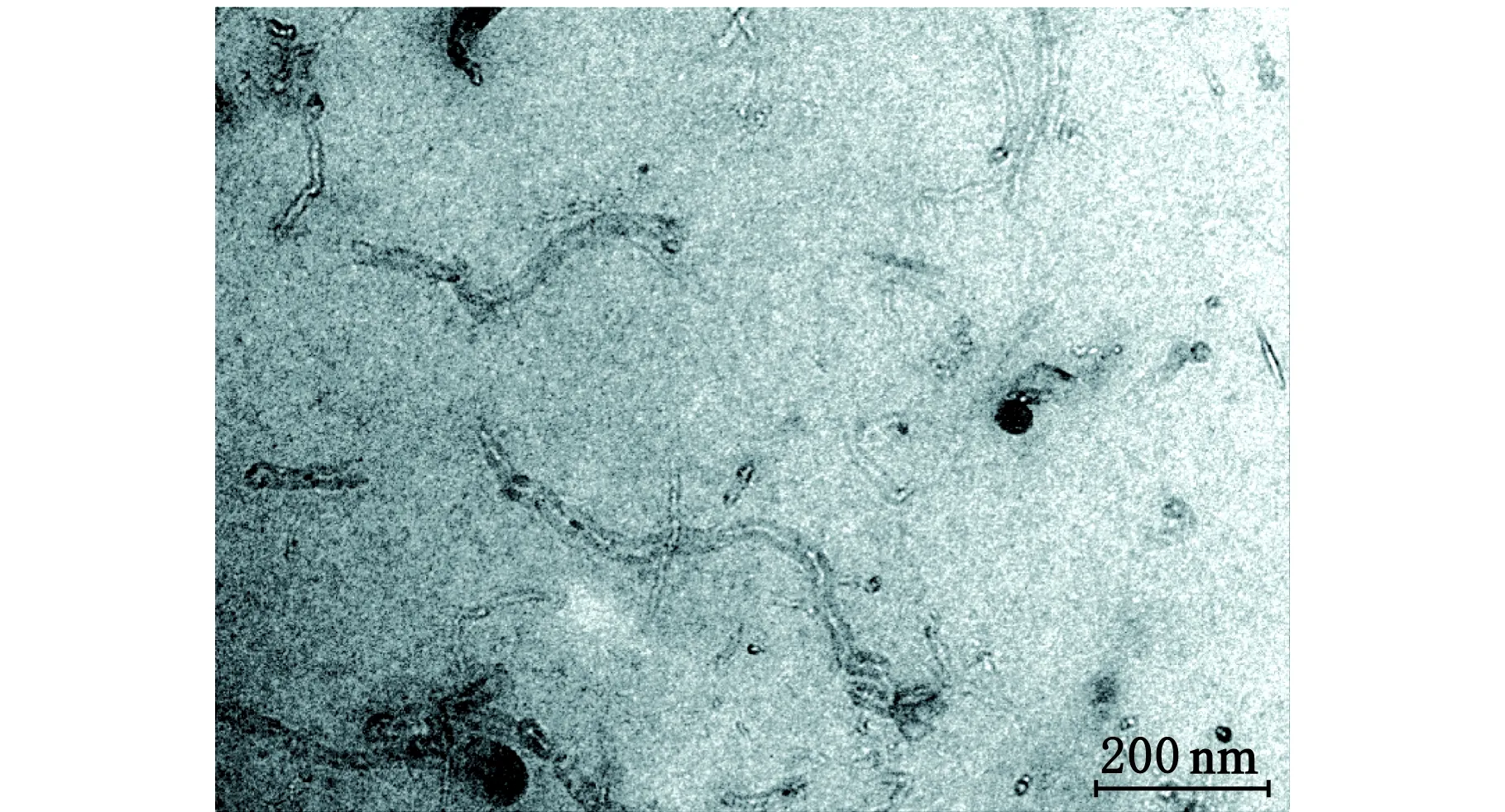
(a) CNT/NR-3

2.2 CNT补强机理的理论研究

由于CNT的结构和表面碳原子的键接方式与纤维不同，根据Halpin-Tsai模型的原理，需将CNT做等效纤维变换，即把CNT补强作为纤维补强进行理论计算[13]。在此基础上，用Halpin-Tsai模型分别对CNT在NR基体中具有一定长径比时处于取向状态、无规取向状态这两种主要情况下对复合材料的力学性能进行了理论计算[10,13-14]。

(1) CNT在复合材料中为取向分布时其杨氏模量EC为[10]：

(1)

(2) CNT在复合材料中为无规取向分布时其杨氏模量EC为[14]：

(2)

其中，根据CNT/NR-3样品的TEM照片统计复合材料中CNT的平均长度和平均直径，以此平均值作为各复合材料样品中CNT的长度和直径，得到其外直径d=17.83 nm，平均长度l=404.44 nm，则长径比l/d=22.68。内直径di=7.5 nm，由此得多壁碳纳米管的厚度t=5.17 nm。因此可求出CNT的等效杨氏模量Eeq=521.43 GPa。

2.3 CNT补强模型计算

首先，根据取向纤维补强模型计算100%、200%、300%定伸强度的理论值，并与实测值进行比较。图3为取向纤维补强模型下复合材料的理论强度与实测值的对比，从理论值与实测值的差值相对于实测值的百分比大小可以看出，理论值比实测值增加的幅度呈现先增大后减小的趋势。理论值与实测值越接近，说明与此种情况越符合。从图3中可以看出，在不同定伸下，随着CNT含量的增加，理论值相对于实测值的增大程度先增大后减小。产生这种情况的原因是在实际的实验过程中，当复合材料中的CNT含量较少时(低于6 phr)，其对基体的补强主要为流体力学的补强，不存在取向对强度的影响。但是理论计算时，已经将取向的贡献计算进去。

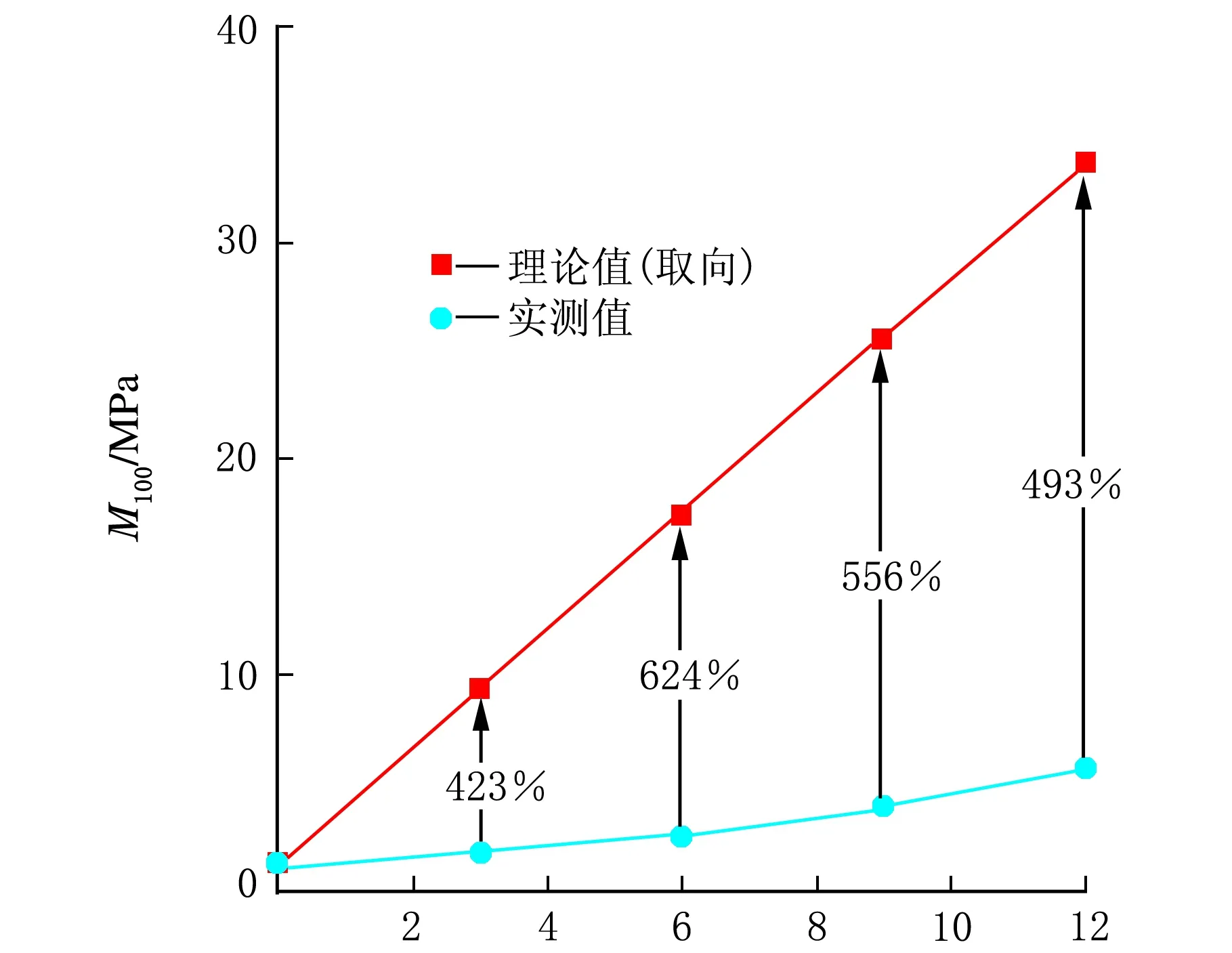
CNT用量/phr(a) 100%定伸强度

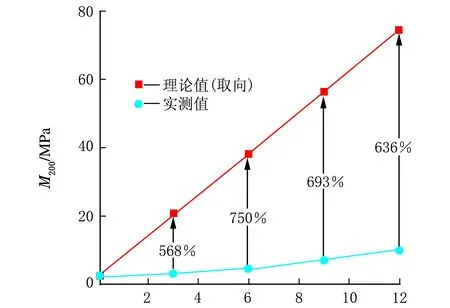
CNT用量/phr(b) 200%定伸强度

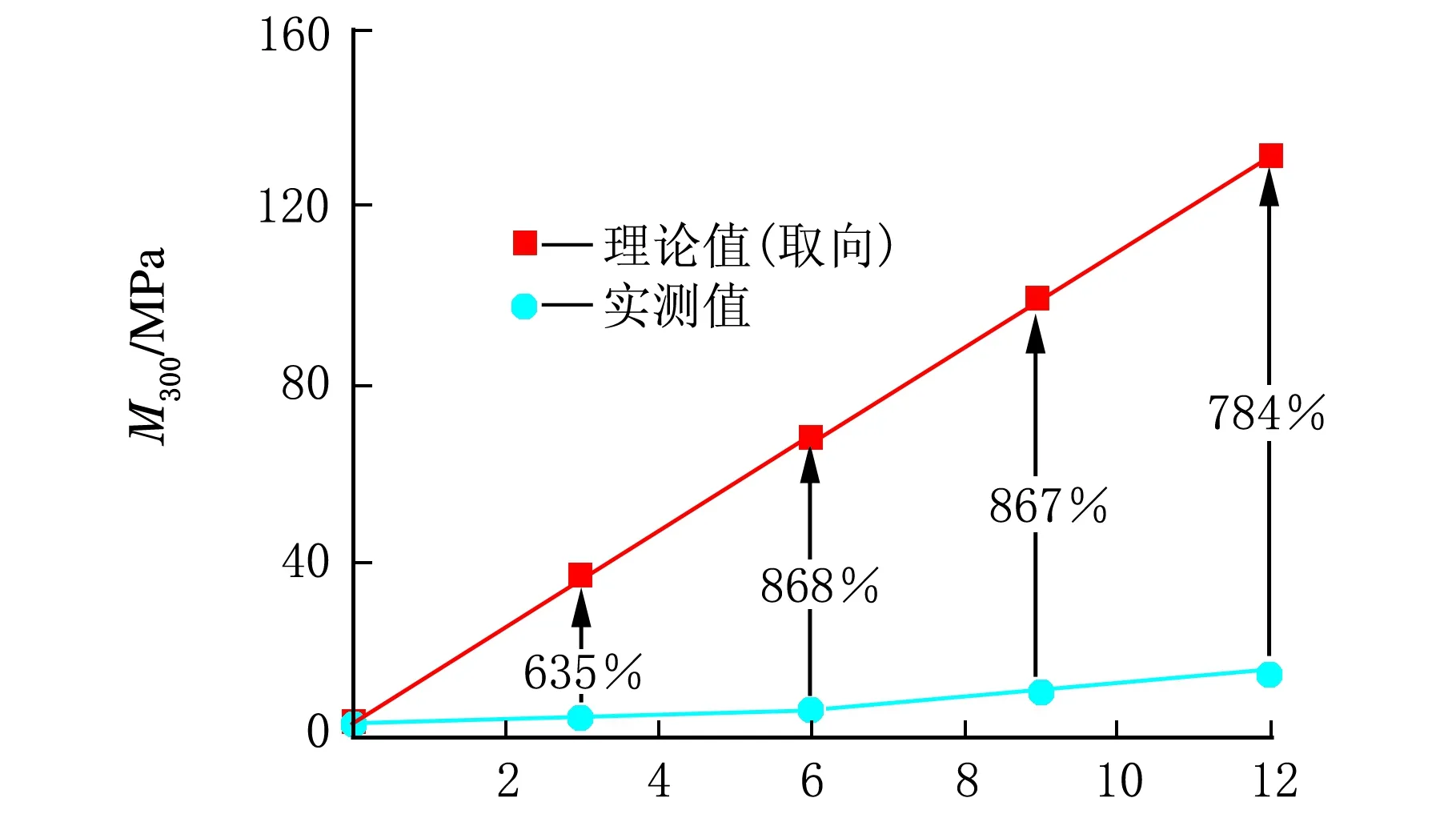
CNT用量/phr(c) 300%定伸强度图3 不同伸长量下CNT含量不同的CNT/NR复合材料的定伸模量的理论值(取向)和实测值

因此，随着CNT含量的增大，理论值比实测值的增加幅度变大；但是，当CNT含量达到一定程度以后(高于6 phr)，结合前期的研究结果[12]，复合材料中的CNT形成三维网络结构且结合橡胶增多，使复合材料的强度提高，从而使实测值与理论值相差幅度变小，但是取向模型得到的理论强度仍然远远高于实际所测强度。基于此，CNT在NR中的取向纤维补强模型并不符合实际的复合材料。

在此基础上，将补强性能的实测值与无规纤维补强的理论力学性能进行比较，结果如图4所示。

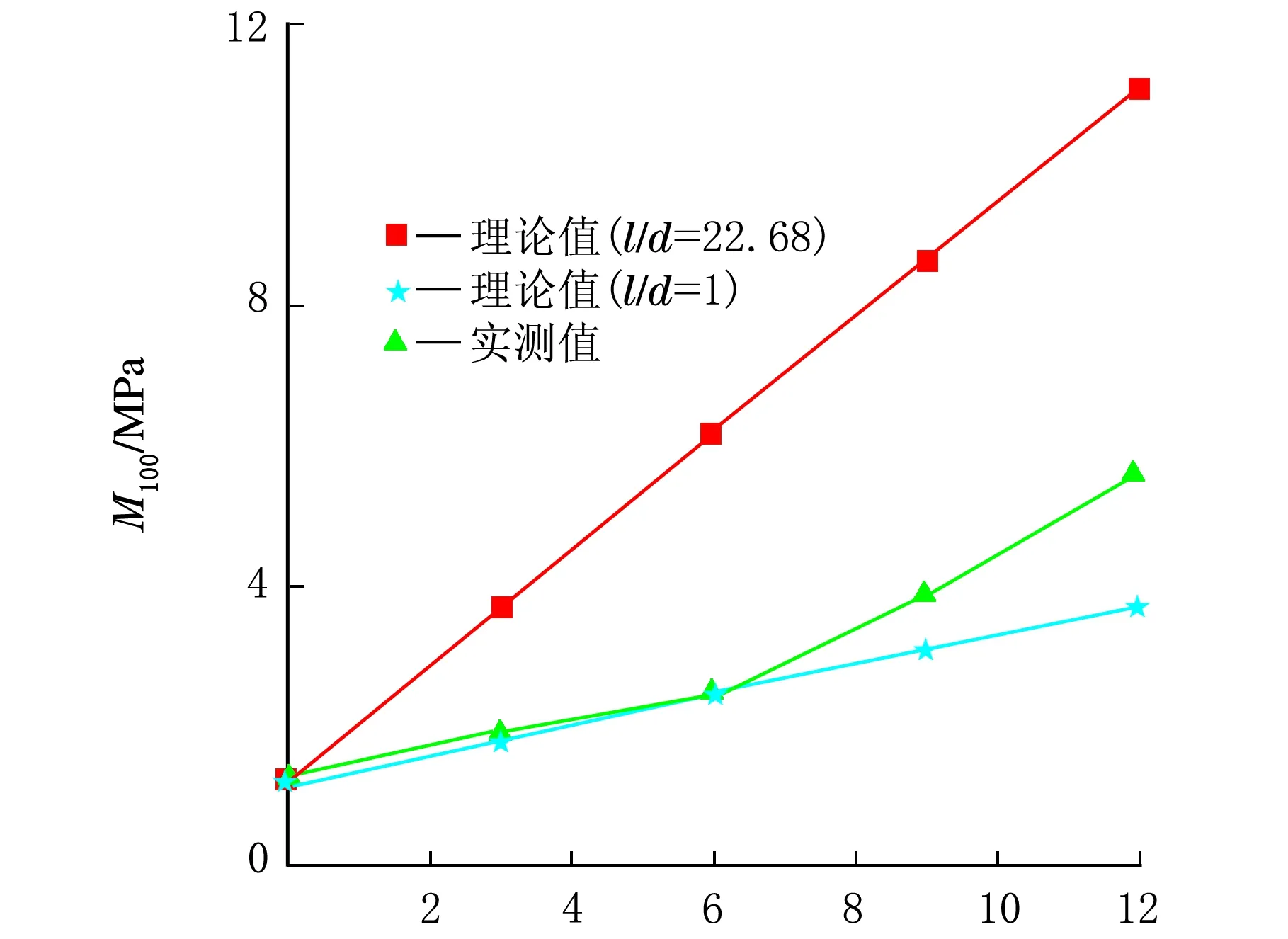
CNT用量/phr(a) 100%定伸强度

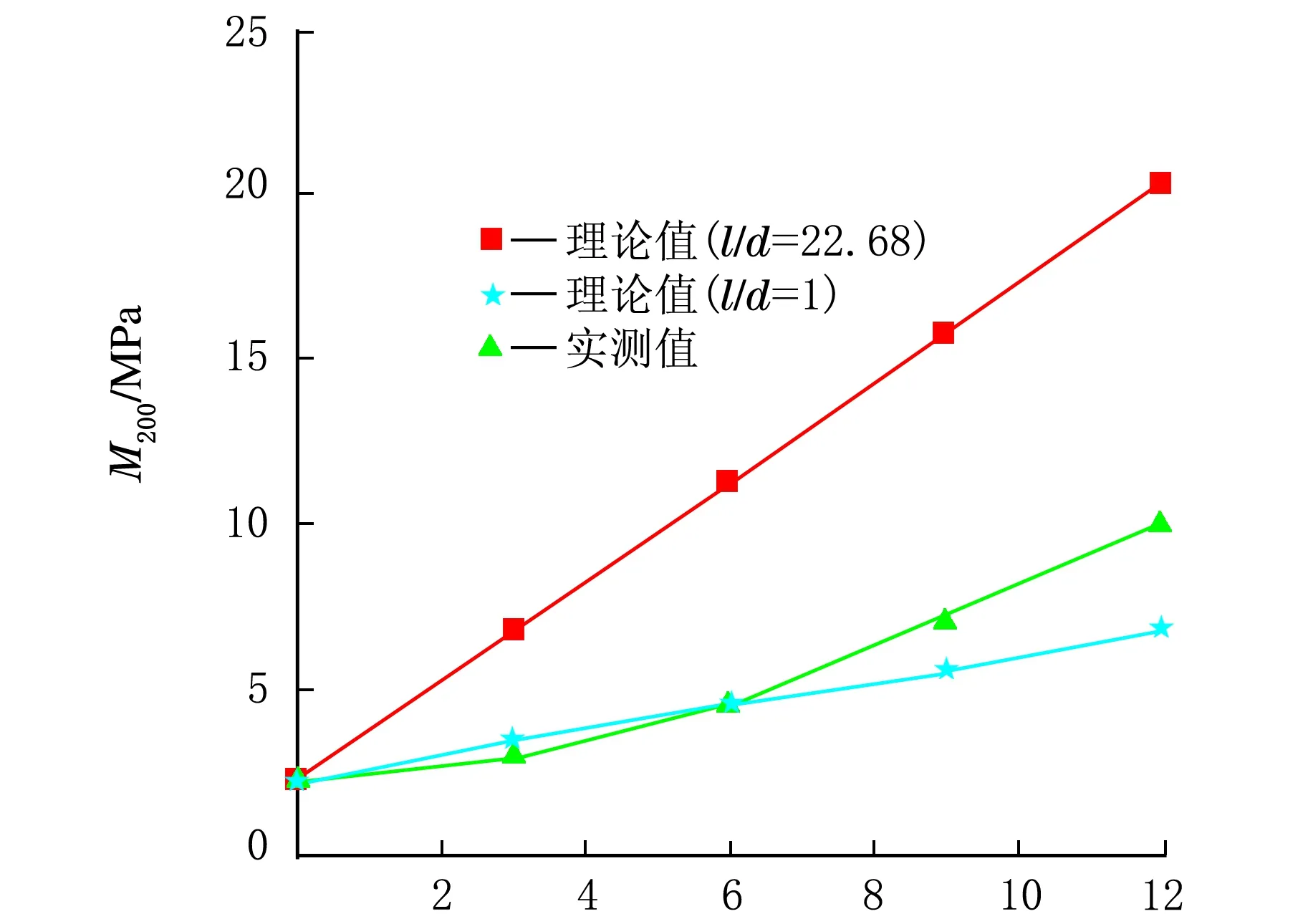
CNT用量/phr(b) 200%定伸强度

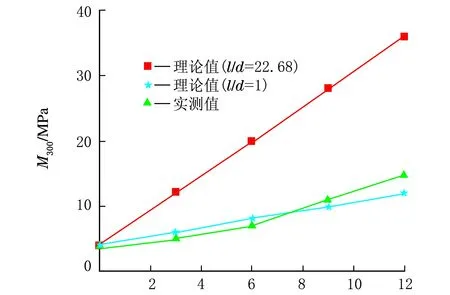
CNT用量/phr(c) 300%定伸强度图4 不同伸长量下CNT含量不同的CNT/NR复合材料的定伸模量的理论值(无规)和实测值

以l/d=1与l/d=22.68作为边界条件与实测值做比较，从图4可以看出，对于CNT/NR复合材料的100%定伸强度来说，当CNT含量较低(3 phr,6 phr)时，实验结果与l/d=1时所计算的理论结果几乎一致，但是随着CNT含量的提高，实验结果与l/d=1时的理论结果相差越来越大，且与无规纤维补强理论结果相差越来越小，但仍小于无规纤维补强的理论结果。产生以上结果的原因是材料在低拉伸情况下，当复合材料中CNT含量较少时，由于混炼过程对CNT的破坏严重，使CNT长径比急剧降低，导致CNT在复合材料中的含量较低时丧失纤维补强效果，所以实验结果与长径比为1时的理论结果较符合。随着CNT含量增高，结合高填充时的电镜照片，具有一定长径比的CNT在复合材料中形成三维网络结构，正是由于这种三维网络结构的存在，使CNT对NR的补强效果显著增强，从而使实验结果越来越接近于无规纤维补强的理论结果。但是对于200%及300%定伸强度来说，CNT含量较低时实验结果要低于长径比为1时的理论计算结果，但是当CNT含量增加到一定量时，实验结果要大于长径比为1时的理论结果，但是小于无规纤维补强的理论计算值，且随着伸长量的增加结果更加接近于长径比为1。产生以上结果的原因是复合材料在高拉伸时，由于伸长率过大，材料自身缺陷的存在以及加工过程中CNT长径比的急剧降低使其小于长径比为1时的理论结果。虽然CNT含量较高时CNT三维网络结构对样品在低拉伸(100%)情况下具有很好的补强效果，但是复合材料中的CNT三维网络结构随着拉伸长度增大将会受到严重的破坏，所以在CNT高填充情况下，随着样品伸长量的增加，实验结果与长径比为1时的理论结果偏差越小，且两曲线的交点位置向高填充方向移动。

基于上述结果可以得出CNT对NR的补强机理。当CNT/NR复合材料中CNT含量较少时，CNT能够独立分散，并且相互之间没有相互作用，但是由于机械混炼对CNT的长度破坏严重，使其失去纤维补强的效果。随着复合材料中CNT含量的增加，即使长径比较小，但仍能使其形成三维网络结构，这使材料在较低的伸长量时具有优异的力学性能，表现出较好的补强效果，可以说CNT具有一定的纤维补强效果。但是随着伸长量的增加，三维网络结构将会被破坏，从而使CNT的补强效果有所下降。对于CNT补强NR复合材料来说，在CNT含量较低时，如果CNT的长径比过小，CNT会失去纤维补强的作用，但是当CNT含量超过一定量时，CNT在CNT/NR复合材料中形成三维网络结构，这种三维网络结构对复合材料具有优异的补强效果。所以长径比对于CNT复合材料的力学性能具有十分重要的意义。

3 结 论

本文制备了不同填料含量(0、3、6、9、12 phr)的CNT/NR复合材料，并对其物理机械性能、结合橡胶含量、CNT的分散性及与NR的相互作用进行了表征。随着CNT含量的增加，复合材料的拉伸强度逐渐增大，结合橡胶含量逐渐增多，CNT及其结合橡胶之间逐渐形成了三维网络。在此基础上，利用Halpin-Tsai模型，分别计算了取向纤维补强、无规纤维补强情况下的理论力学性能，并与实验所得结果进行比较，得到了CNT对NR的补强机理：(1)当CNT用量小于6 phr时，由于CNT的长径比过小，失去纤维补强的作用；(2)当CNT用量大于6 phr时，在应变较小时，CNT在复合材料中形成的三维网络结构使复合材料的力学性能有很大的提高，使CNT即使在长径比较小的情况下依然能够发挥其纤维补强效果；(3)随着应变的增加，三维网络结构遭到破坏，CNT纤维补强效果减弱。

参 考 文 献：

[1] LIJIMA S.Helical microtubules of graphitic carbon[J].Nature,1991,354(6348)：56-58.

[2] VERMA P,SAINI P,MALIK R S,et al.Excellent electromagnetic interference shielding and mechanical properties of high loading carbon-nanotubes/polymer composites designed using melt recirculation equipped twin-screw extruder[J].Carbon,2015,89：308-317.

[3] WEN B,CAO M S,HOU Z L,et al.Temperature dependent microwave attenuation behavior for carbon-nanotube/silica composites[J].Carbon,2013,65：124-139.

[4] 许图远,王松,卢咏来,等.碳纳米管/橡胶复合材料的研究进展[J].合成橡胶工业,2011,34(6)：489-494.

[5] 刘乃亮,赵红振,齐暑华,等.碳纳米管/橡胶复合材料研究进展[J].合成橡胶工业,2008,31(4)：315-318.

[6] PATOLE A S,PATOLE S P,JUNG S,et al.Self-assembledgraphene/carbon nanotube/polystyrene hybrid nanocomposite by in situ microemulsion polymerization[J].European Polymer Journal,2012,48(2)：252-259.

[7] ROBINSON I M,ROBINSON J M.The effect of fibre aspect ratio on the stiffness of discontinuous fibre-reinforced composites[J].Composits,1994,25(7)：499-503.

[8] ESHELBYJ D.The determination of the elastic field of an ellipsoidal inclusion and related problems[J].Proceedings of the Royal Society of London,1957,241(1226):376-396.

[9] TANDONG P,WENGG J.The effect of aspect ratio of inclusions on the elastic properties of unidirectionally aligned composites[J].Polymer Composite,1984,5(4)：327-333.

[10] MALLICK P K.Fiber-reinforced composites[M].New York：Dekker,1993：130-132.

[11] DENG F,ITO M,NOGUCHIT,et al.Elucidation of the reinforcing mechanism in carbon nanotube/rubber nanocomposites[J].American Chemical Society,2011,5(5)：3858-3866.

[12] 张亭亭.碳纳米管/天然橡胶复合材料的加工工艺—结构—性能研究[D].青岛：青岛科技大学,2014.

[13] THOSTENSON E T,CHOU TW.On the elastic properties of carbon nanotube-based composites：Modelling and characterization[J].Journal of Physics D：Applied Physics,2003,36(5)：573-582.

[14] LANDEL R F,NIELSEN L E.Mechanical properties of polymers and composites[M].Boca Raton：CRC Press,1993：145-150.

[15] QIAN D,DICKEY E C,ANDREWS R,el al.Load transferand deformation mechanisms in carbonnanotube/polystyrenecomposites[J].Applied Physics Letters,2000,76(20)：2868-2870.