基于投资者情绪的AH股条件资产定价研究

孟卫东++张梦雨++陆静

摘要：文章采用主成分分析法分别构造AH股市场综合情绪指数，再运用条件贝塔参数随着投资者情绪和公司特征值变化的两阶段条件资产定价模型进行实证分析，结果表明：加入投资者情绪的条件定价模型，AH股定价的规模效应变得不显著，A股定价的B/M效应显著性明显下降，因此投资者情绪可以帮助定价模型捕捉股票定价异象，但A股定价受投资者情绪影响程度强于H股，不同市场的投资者情绪对资产定价影响程度差异是导致AH股双重上市公司同股不同价的原因之一。

关键词：投资者情绪；AH股价差；股票定价异象；条件资产定价模型

中图分类号：F83091文献标志码：A文章编号：

10085831（2016）02008010

一、研究问题与背景

在市场分割的条件下，具有相同企业背景和未来现金流的AH股双重上市公司股票长期以来存在着同股不同价的现象，虽然其他国家、地区的资本市场上亦有类似现象，但中国是唯一一个内资股相对于外资股存在较大幅度溢价的国家，这种现象被Fernald和Rogers[1]称为“中国股票市场之迷”。这种“中国特例”在一定程度上反映了中国股票市场的制度和投资者构成等特点。因此，研究分析导致A股与H股价格差异的因素，有助于深入了解中国大陆股票市场与香港股票市场的差异性，为中国证券市场的完善运行提供有力的理论参考。

众多学者对AH股价差的影响因素进行了探讨，但大都局限于传统金融领域。Fama[2]在1970年提出的有效市场假说认为资本市场上的行为人均为“理性经济人”，而投资者情绪作为一种背离理性的投资人心态，不会对股票价格和收益率产生影响。然而随着学者们对金融市场的研究不断深入，发现股票收益并不仅仅由股票市场风险决定，资本市场仍然存在很多传统资本资产定价模型（CAPM）无法解释的异象，如规模效应[3]、价值效应[4]和动量效应[5]等。行为金融学从投资者心理偏差视角对股票市场异象作出解释。Baker和Wurgler[6]对投资者情绪给出了两个经典定义：投资者情绪描述了投资者的投机倾向，投资者情绪的高低通过影响投资者的投机需求，进而影响股票收益；投资者情绪的高低反映了投资者对市场的悲观或乐观的心态，影响了套利行为的风险及成本，进而影响股票收益。因此，投资者情绪可以通过影响投机需求和市场套利行为，导致资本市场股票错误定价。2014年11月17日起，沪港通的正式实施给AH股市场提供了较好的套利通道，从理论上讲AH价差应该进一步缩小，然而，自沪港通开通以后，多数AH股价差不降反升，截至2014年12月31日，恒生AH溢价指数最高触及12878点，创下近三年来的新高。不可否认，这与2014年末A股进入牛市紧密相关，因此需要我们从投资者情绪的角度去解释A股市场长期存在的非理性繁荣。

本文以AH股双重上市公司股票为样本，采用Baker和Wurgler[6]的主成分分析法分别构建了A股市场和H股市场的月度综合情绪指数，并将Avramov和Chordia[7]构建的两阶段条件资产定价模型框架（The twopass conditional framework）予以延伸，使资产定价模型中的Beta参数随着投资者情绪和公司特征值（市值和账面市值比）变动，通过时间序列回归和横截面回归，分析将投资者情绪作为条件信息加入时变的贝塔参数之后，是否有助于条件资产定价模型解释A股和H股市场规模效应、价值效应、流动性效应和动量效应等股票市场定价异象，并探究不同市场投资者情绪对A股、H股市场资产定价的影响程度差异，结合AH股市场环境、制度和投资者组成等方面的差异，从投资者情绪角度解释AH股价差。

本文的主要贡献有以下三点：（1）打破了传统金融理论的局限，从行为金融学理论出发，创新地将投资者情绪作为条件信息加入条件定价模型，给研究国内外资本市场定价异象提供了新的方法；（2）从投资者情绪的角度去认识AH股定价差异，有利于中国相关部门认清A股市场投资者严重的投机心理和市场情绪化倾向，对于预警中国资本市场泡沫，完善和发展中国资本市场都有重要的指导意义；（3）本文的研究将行为金融学理论和含有投资者情绪的条件资产定价模型推广到跨市场交叉上市股票价差研究领域，为该领域提供了一套更加实用的指导性工具。

二、文献回顾

A股和H股长期存在的价差问题一直受到国内外众多学者的关注，他们分别从流动性差异、需求差异、汇率风险差异以及信息非对称方面对AH股的价差作出解释[8-12]。20世纪60年代提出的资本资产定价模型（CAPM）是现代金融理论的基石，然而70年代在股票横截面收益中涌现的大量投资者异常行为和金融市场异象，让学者们纷纷对传统CAPM模型的有效性提出质疑，Fama和French[13]将市值（size）和账面市值比（B/M）加入定价模型中，并提出市值和账面市值比这两因子解释股票市场横截面收益的能力强于单一的市场系统风险因子Beta，但是Fama-French三因子模型仍然没有解释动量效应。因此，学者们开始尝试从行为金融学的角度去解释这些股票市场异象，而投资者情绪作为行为金融学重要的研究主题，成为了国内外学者的研究热点。已有研究成果表明：投资者情绪可以作为未来现金流和投资风险的信念，与股票横截面收益有着显著的相关性，是影响资产定价的重要因素之一[14-17]。

与静态的无条件资产定价模型相比，条件资产定价模型中考虑了风险Beta参数的多变性，因此其解释股票横截面收益的能力优于无条件定价模型[18]。已有学者发现公司市场特征值[19]和宏观经济变量[20]在预测投资组合期望收益方面有着显著的时变性。近年来越来越多的研究将重点放在动态的条件资产定价模型的研究上：Lettau和Ludvigson[21]将期限溢价、违约利差和消费—财富比（Consumption-Wealth Ratio）作为条件变量加入条件定价模型；Gomes[22]用股利价格比（D/P）、账面市值比和公司市值等公司特征值去测量Beta参数；Ho和Huang[23]将投资者情绪作为条件信息加入时变的Beta参数，有助于深入观测投资者情绪对风险因子敏感性的影响，并发现投资者情绪是有效的条件信息之一。

本文的研究与国内外同类研究的区别主要在于：（1）目前基于条件资产定价模型对股票市场收益的影响研究，其研究主体大多局限于发达资本市场的股票，而对新兴资本市场，尤其是对于中国股票市场的研究较少，而本文的研究主体是同时在中国大陆和中国香港两个新兴资本市场交易的股票；（2）目前国内关于投资者情绪研究的文献中，大多仅将投资者情绪作为股票市场超额收益率的解释变量，通过横截面回归分析它与股票市场超额收益率的相关性，而本文将投资者情绪作为条件信息加入资产定价模型，研究中国股票市场的定价异象；（3）Ho和Huang的研究只针对单一的美国资本市场，没有涉及跨市场的投资者情绪对交叉上市公司条件资产定价模型的影响，而本文以双重上市的AH股公司为样本，旨在比较双重上市股票定价如何受到不同地区情绪的影响，该方法在国内外研究中属首创。

三、市场综合情绪值的构造

研究投资者情绪的关键是构造一个合理的投资者情绪指数，学者们早期的研究往往将某单一的指数作为反映市场投资者情绪的代理指标，探究它们对股票市场收益和流动性的影响，但具体哪一个情绪代理指数能够最直接地反映股票市场上投资者情绪的变化，国内外学者尚未达成一致结论。单一的情绪代理变量有两方面的缺陷：一是单一的情绪代理指数具有片面性，不能全面反映整个市场的投资者情绪；二是单一的情绪代理指数由于含有该指标本身特有的信息，不能够准确地反映市场投资者的情绪信息。为了改善单一情绪代理变量在研究中的局限性，我们采用Baker和Wurgler提出的构造综合情绪的方法，分别构造A股和H股市场的投资者综合情绪代理指数。

（一）市场综合情绪指数的构造方法

构造综合情绪指数的步骤如下：（1）选取几个合适的情绪代理指标；（2）判断所选指标是否采用滞后一期值，根据Baker和Wurgler采用的主成分分析法，将选取的单一情绪指数标准化之后的当期值和滞后一期值进行第一次主成分分析，选取特征根大于1的主成分，用特征值进行加权平均构造一个中间指数，然后再进行相关性检验，根据所选指标当期值和滞后项与中间指数的相关性大小，决定选取该指标是否采用滞后项；（3）用选定的指标与宏观经济变量进行正交化处理，为了排除选定的情绪代理指标本身特有的宏观经济信息的干扰，使其只包含投资者情绪信息，我们将其与宏观经济变量进行回归，提取回归残差项作为更准确的情绪代理指标，去构造投资者综合情绪值；（4）用正交之后的情绪代理指标进行第二次主成分分析，同样提取特征根大于1的主成分，构造综合情绪指数。为了保证构造的综合情绪指数能够充分反映整个市场的投资者情绪波动，我们严格遵循主成分累计解释力大于70%的准则。

由于A股和H股市场发展程度和成熟度不同，能够直观反映这两个市场投资者情绪的情绪代理指标也不同，我们分别选取若干个可以更准确反映A股和H股市场投资者情绪变化的情绪代理指标，通过上述方法，分别构建A股市场投资者综合情绪指数和H股市场投资者综合情绪指数。

（二）A股和H股市场投资者综合情绪指数

根据已有研究成果[24-27]，在构造A股市场投资者综合情绪指数时，本文引入了封闭式基金折价率、消费者信心指数、新增开户数、市盈率和换手率这5个综合情绪指数组成指标。

我们将A股市场上述5个情绪代理指标月度数据当期值和滞后一期值标准化后，用前文提到的主成分分析法进行市场投资者综合情绪值的构造，样本区间为2003年1月至2013年12月，其中：由于换手率在样本期间内呈现了一种指数型正向趋势，为了去除这种趋势，我们将原始的换手率值取自然对数后，再进行5年移动平均处理；另外，我们选取居民消费者指数（CPI）、净出口（NEX）和工业增长率（IGR）这3个宏观经济指标对选定的代理变量当期值或滞后项进行正交化处理。最终我们构造的A股市场综合情绪指数表达式如下：

SentA⊥t=-0.401 9CEFD⊥t-1+0435 5CCI⊥t-1+1.318 2NSA⊥t+1.348 9PE⊥t+1.276 0Turnover⊥t-1

（1）

CEFD⊥表示经正交化处理后的封闭式基金折价率；CCI⊥表示经正交化处理后的消费者信心指数；NSA⊥表示经正交化处理后的新增开户数；PE⊥表示经正交化处理后的市盈率；Turnover⊥为经正交化处理后的市场换手率；每个代理指标下缀t和t-1分别表示该指标当期值和滞后一期值。通过主成分分析构造的A股市场投资者综合情绪指数累计解释力为7250%，因此我们认为该综合情绪指数涵盖了A股市场大部分投资者情绪波动。

与A股市场相同，我们在构造H股市场投资者综合情绪指数时同样选取了封闭式基金折价率、换手率作为情绪代理变量。由于H股是较为成熟的市场，机构投资者偏多，因此消费者信心指数、新增开户数、市盈率受投资者情绪影响不如A股市场明显。为了更好地体现H股市场投资者情绪变化，我们选取了IPO数量、IPO首日收益率、市场交易量和股本发行量作为衡量H股投资者情绪代理指标[28-30]。

同样地，我们对H股市场上述投资者情绪代理变量月度当期值和滞后项数据进行标准化处理，换手率取自然对数后，5年移动平均去趋势化处理，以及与宏观经济变量CPI和货币供应量（M3）正交化处理，样本区间同样为2003年1月至2013年12月。最终得到的H股市场投资者综合情绪指数为：

SentH⊥t=-0.352 7CEFD⊥t-1+0371 4NIPO⊥t-1+1.398 8RIPO⊥t+0.464 8Share⊥t+1.428 7Turnover⊥t-1

（2）

其中，NIPO⊥代表每月IPO数量，RIPO⊥代表每月IPO首日收益率，Share⊥代表普通股份额。通过主成分分析构造的H股市场投资者综合情绪指数累计解释力为73%，因此我们认为该综合情绪指数涵盖了H股市场大部分投资者情绪波动。

四、研究设计

（一）第一阶段时间序列回归模型的建立

1静态的无条件资产的定价模型

本文主要以资本资产定价模型（CAPM）和Fama-French三因子模型（FF）为基础进行实证回归分析。传统的无条件资产定价模型假设风险参数Beta为恒定不变，故无条件的CAPM模型与无条件的FF模型的表达式如下所示。

（1）无条件的资本资产定价模型。

rit=αi+βiMRMt+εit（3）

其中，rit=Rit-Rft为个股超额收益率，Rit为个股i在t时刻的收益率，Rft为无风险收益率；RMt为市场指数在t时刻的超额收益率，εit为误差项。CAPM模型是最基本的资产定价模型，其中只包含了1个风险因子，即是市场投资组合的超额收益，该风险因子的风险系数βiM为常数。

（2）无条件的Fama-French三因子模型。

rit=αi+βimRMt+βiSMBSMBt+βiHMLHMLt+εit（4）

其中，SMBt为时期t的市值因子的模拟组合收益率，HMLt为时间t的账面市值比因子的模拟组合收益率。Fama和French认为，包含了市场投资组合（

Rmt）、市值因子（SMB）、账面市值比因子（HML）这3个风险因子的资产定价模型可以更好地解释单个股票或投资组合的超额回报率，同样的，3个风险因子的风险系数（

βim，βiSMB和βiHML）均为常数。

2时变的条件资产定价模型

静态的无条件资产定价模型忽略了风险因子的时变性，因此无法完全解释股票市场上的超额收益率。已有研究表明，公司特征值在预测投资组合收益方面具有显著的时变性，应作为条件信息加入条件资产定价模型的Beta参数。基于投资者情绪可以反映金融市场目前的状况和未来的前景，本文将投资者情绪同样作为条件信息加入条件资产定价模型。

接下来本文以最简单的CAPM模型为例，对时变的条件资产定价模型进行描述。无条件的资产定价模型假定模型中风险因子的Beta系数是恒定不变的，而本文提出风险参数

βit-1

是随着市场投资者情绪（Sentt-1）和公司特征值（SIZEit-1、B/Mit-1）时变的，时变的Beta参数可以用以下公式表示：

βit-1=βia+βibsentt-1+（βic+βidSentt-1）SIZEit-1

+（βie+βifSentt-1）（B/M）it-1（5）

若为无条件定价模型，那么除了βia之外的所有βiS均为0，即β为常数。根据式（5）我们可以构造3个不同的时变风险β参数，其表达式如下。

（1）参数A：用包含了投资者情绪，公司市值和账面市值比三个解释变量的表达式表示，即式（5）中所有的βiS均不为0；

（2）参数B：用包含了公司市值和账面市值比两个公司特征值的表达式表示，即式（5）中βib=βid=βif=0；

（3）参数C：用只包含投资者情绪变量的表达式表示，即式（5）中βc=βd=βe=βf=0。

因此，含所有条件信息的风险参数A的条件CAPM模型如下所示：

rit=αi+βiaRMt+βibSentt-1RMt+βicSIZEit-1RMt+βidSentt-1SIZEit-1RMt+

βieB/Mit-1RMt+

βifSentt-1B/Mit-1RMt+Dummy1+Dummy2+εit

（6）

其中，投资者情绪和公司特征值为滞后一期变量。为了使回归结果更稳健，我们在模型中加入2个宏观经济变量的虚拟变量：Dummy1代表中国汇改的虚拟变量，2005年7月21日汇率制度机制改革之前取0，汇率机制改革形成之后取1；Dummy2代表A股股改虚拟变量，A股股改完毕之前取0，A股股改完毕之后取1。

本文分别对无条件资产定价模型和含有不同条件信息的条件资产定价模型进行时间序列回归，得到的截距项和误差项之和（R*it=αi+εit）为风险调节收益。

（二）第二阶段横截面回归模型的建立

我们将第一阶段时间序列回归中的截距项（定价误差，pricing error）和残差项之和（风险调节收益）作为被解释变量，再使其与公司市值、账面市值比、换手率以及累计收益率等公司特征值进行横截面回归。原假设为在第一阶段时间序列回归过程中，定价模型有效地捕捉了股票市场异象，因此，在第二阶段横截面回归模型中，公司市值、账面市值比、换手率以及累计收益率与风险调节收益没有显著的相关性。综上，我们将第二阶段横截面回归模型归纳为以下的一般形式：

R*it=α0t+γsize，tSIZEt-1+γBM，tBMt-1+γturn，tTURNt-1+

γRET，tRETt-1+πit

（7）

其中，R*it代表股票i在t时刻的风险调节收益，它等于第一阶段时间序列回归中截距项和残差项的总和；式（7）中的解释变量分别为公司市值（Size）、账面市值比（BM）、换手率（TURN）和个股累计收益率（RET）；γcharacter，t代表特征值与风险调节收益的相关系数。

式（7）所描述的横截面回归将个股每月的风险调节收益与公司市值、账面市值比、换手率和累计收益率进行回归，如果回归结果接受原假设，即规模效应、价值效应、换手率效应、动量效应等定价异象的系数均为零并且结果在统计学上不显著。回归结果中调整后的R方（R2）可以用作比较不同的条件Beta参数的定价模型整体表现的指标。较小的R2说明第一阶段时间序列回归中的资产定价模型对股票收益有较强的解释力。在横截面回归中，参考Ho和Huang的方法，解释变量将采用公司特征值的偏差（即减去样本平均值）进行回归分析，这暗示着对于每一个无风险的公司特征值，股票的平均价值为零，因此只有风险因子可以决定股票的预期收益。同时，为了避免风险调节收益受到股票市场上买卖效应和交投疏落的影响，我们采用公司特征值的滞后变量进行回归。

五、实证分析

（一）样本选取与数据来源

截至2014年12月，已有86家公司成功实现AH股双重上市，为了保证样本交易数据具有时效性、合理性以及普遍性，我们要求所选取的公司样本同时具有A股和H股市场上市3年的交易数据，因此我们剔除了23家2011年之后才完成双重上市的公司；另外，剩下的样本中含8家经过特殊处理（ST或PT）的公司，价格具有特殊性，我们同样将其从样本中剔除，将最后剩下的55家AH股双重上市公司作为本文研究样本。

（二）第一阶段时间序列回归中α显著性检验

通过第一阶段对个股月超额收益的时间序列回归得到的截距项被定义为定价误差，它代表着超额收益中未被定价模型中风险因子解释的那一部分收益。如果加入条件信息的条件定价模型能够完全解释股票市场横截面的平均回报率，那么时间序列回归中的截距项应该全部显著为0。我们根据Shanken的方法，将条件αit用含有条件信息解释变量（conditioning instruments）的线性公式表示：

αit=αi0+αi1Xit（8）

其中，αi0为标量，αi1为线性回归参数矢量，Xit为条件αit的条件信息变量（投资者情绪、Size和B/M比率）的矢量，有以下四种情况。

（1）若为无条件定价模型（UNCOND），Xit中不含任何条件信息，则Xit=0；

（2）当条件资产定价模型中风险参数为A时，Xit=Xit（Sent；Sizet；BMt）；

（3）当条件资产定价模型中风险参数为B时，Xit=Xit（Sizet；BMt）；

（4）当条件资产定价模型中风险参数为C时，Xit=Xit（Sent）。

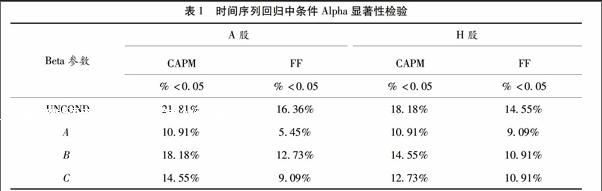
为了检验本文中的条件定价模型是否完全解释条件预期收益，即定价误差为0，我们对原假设：条件αi0=0（αi0=αi1=0），进行F检验。表1报告了样本公司在时间序列回归中得到的条件αit的显著性检验结果。

表1中的数据为p-value小于005的样本公司占比，当p-value小于005时，我们拒绝原假设，条件αit显著不为0。以A股CAPM模型为例，在5%的水平下，无条件定价模型（UNCOND）条件αit拒绝为0的公司比例为2181%；加入条件信息以后，条件αit拒绝为0的公司比例下降到1818%与1091%之间；参数A所对应的条件定价模型，包含了所有的条件信息，在预测预期收益时的表现优于其他条件定价模型，仅有1091%的公司拒绝原假设。基于A股的FF模型以及H股的CAPM模型、FF模型的显著性检验也得能得到相似结论。因此，我们认为条件定价模型解释投资组合预期收益的能力的确优于无条件定价模型。

（三）第二阶段横截面回归分析

1A股市场横截面回归结果

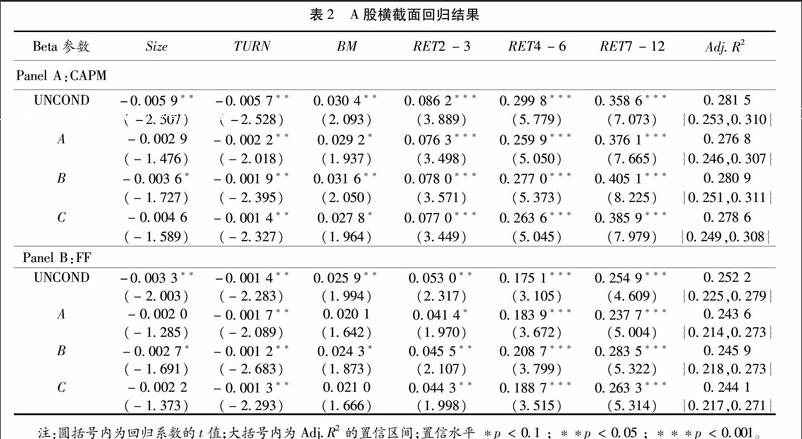
接下来我们通过横截面回归结果，探究无条件定价模型和含有不同时变风险参数的条件定价模型对股票市场定价异象的解释能力。我们将样本公司在A股市场的风险调节收益作为被解释变量（第一阶段时间序列回归截距项与残差项之和）与股票异象解释变量（Size，B/M，换手率与RET2-3，RET4-6，RET7-12）进行横截面回归，得到结果如表2所示。表2中，Panel A报告的是基于无条件CAPM模型和条件CAPM模型的回归结果；Panel B报告的是基于无条件的FF模型和条件FF模型的回归结果。表中第一列列出了无条件的定价模型（UNCOND）和不同条件Beta参数（参数A、参数B和参数C）的条件定价模型；随后几列数据所报告的是各解释变量在横截面回归中的系数以及系数对应的t值；最后一列呈现的是基于不同定价模型的横截面回归调整后的R方均值以及对应的置信区间。

我们可以从以下三个方面对表2的回归结果进行分析。

（1）无条件CAPM模型与条件CAPM模型的对比。

首先，无条件（UNCOND）的CAPM模型的回归结果显示，Size、Turn、B/M和RET的系数全部不为0且显著，即市场规模较小、流动性较弱、账面市值比较高以及过去收益较高的股票有着较高的风险调节收益，无条件的CAPM模型不能解释任何股票定价异象，因此，无条件定价模型关于个股市场Beta恒定不变的假设是有误的。其次，在随后三个条件CAPM模型相对于无条件的CAPM模型，Size、Turn、B/M和RET2-3，RET4-6的系数的t值均有所下降，说明时变的Beta参数解释股票市场异象的能力优于恒定不变的Beta参数。再次，仅将公司特征值作为条件信息（参数B）加入条件CAPM中，Size系数的t值绝对值为1727，A股市场规模效应仍然显著，但将投资者情绪作为条件信息加入Beta参数后（参数A），Size系数的t值绝对值从2507下降到了1476，Size效应变得不再显著，因此，将投资者情绪作为条件信息加入条件CAPM模型，可以帮助模型有效地捕捉A股市场的规模效应，Ho和Huang在对美国股市定价异象的横截面回归中也得到了相似结论；另外，对比参数B和参数C的条件CAPM模型回归结果发现，仅含有投资者情绪的参数C的Size系数和BM系数的t值绝对值（分别为1589和1964）均低于仅含有公司特征值的参数B对应的t值（1727和2050），显著性也有明显下降，说明投资者情绪是更有效的条件信息，比公司特征值更能够捕捉A股市场上的Size效应和BM效应。最后，对比三个条件CAPM模型的AdjR2，加入投资者情绪（参数A和参数C）的条件CAPM的AdjR2小于参数B的条件CAPM模型，因此，加入投资者情绪可以优化条件CAPM预测A股市场上投资组合收益率的能力。

（2）无条件FF模型和条件FF模型的对比。

同样的，由于假定Beta参数恒定不变，横截面回归结果中，无条件的FF模型中所有解释变量的系数均不为0且显著，因此，无条件的FF模型同样无法捕捉任何股票市场定价异象；仅含有公司特征值（参数B）的条件FF，Size系数的t值绝对值和BM系数的t值有所下降，但其规模效应和价值效应仍呈现弱显著性，而在条件FF中加入投资者情绪作为条件信息之后，Size系数的t值的绝对值从2003下降到1285（参数A），BM系数的t值从1994下降到1642（参数A），Size效应和BM效应变得不再显著，说明投资者情绪是有效的条件信息之一，有助于条件FF模型有效地解释股票市场的规模效应和价值效应。与CAPM类似地，参数C的条件FF捕捉Size效应和BM效应的能力优于参数B的条件FF模型，说明投资者情绪作为条件信息比公司特征值更有效。我们从表2-Panel B的回归结果中得到，加入投资者情绪之后，股票市场上短期动量效应显著性下降，表现在解释变量RET2-3的t明显下降，从2317（UNCOND）分别下降到1970（参数A）和1998（参数C）。Avramov和Chordia在类似研究中没有将投资者情绪作为条件信息加入条件资产定价模型，他们的实证结果显示条件的FF模型不能解释股票市场定价的动量效应。因此，本文认为投资者情绪在捕捉股票市场动量效应方面发挥着重要作用。

（3）单因子CAPM模型和三因子FF模型的对比。

对比Panel A和Panel B的回归结果，无条件FF模型中所有解释变量的t值的绝对值均小于无条件CAPM模型中解释变量的t值，因此，加入SMB和HML风险因子可以改善定价模型对A股市场上投资组合收益的预测能力。此外，条件FF模型的AdjR2均小于无条件的FF模型和所有的CAPM模型的AdjR2，再次验证了三因子的FF模型在资产定价方面的表现优于单因子的CAPM模型。

2H股市场横截面回归结果分析

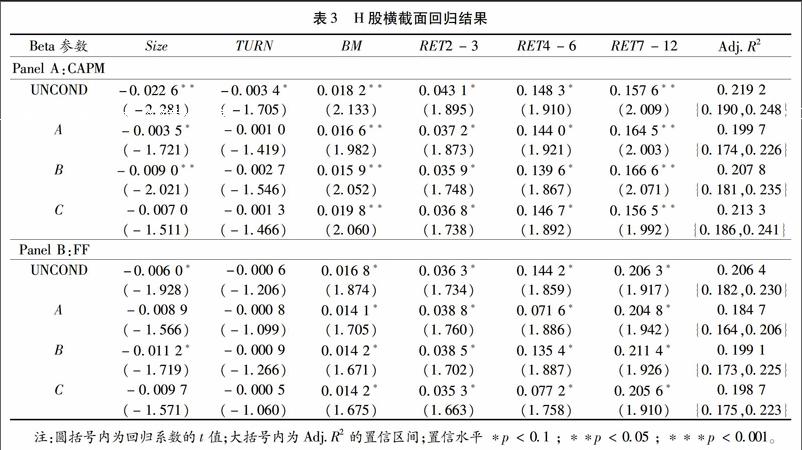
与前文相似，我们同样从三个方面分析H股的横截面回归结果（表3）。

（1）无条件CAPM模型与条件CAPM模型的对比。

首先，在无条件的CAPM模型中，所有解释变量的系数均不为0且显著，说明无条件的CAPM模型无法捕捉H股市场的股票定价异象；在条件CAPM中，解释变量TURN的系数的显著性明显下降，说明时变的Beta参数可以成功捕捉H股市场的流动性效应；对比参数B和参数A的条件CAPM模型，我们发现参数B的条件CAPM中Size系数的t值绝对值虽然相对于UNCOND有所下降，但是H股市场上的Size效应仍然显著，但将投资情绪作为条件信息加入条件CAPM模型以后，H股市场的规模效应显著性降低，Size系数的t值绝对值从2281（UNCOND）下降到1721（参数A），同样说明了投资者情绪有助于条件CAPM模型捕捉H股市场上的规模效应。其次，对比参数B和参数C的条件CAPM模型：参数B的Size系数t值绝对值为2021，规模效应仍然显著，而参数C的条件模型规模效应变得不再显著，说明投资者情绪捕捉H股市场规模效应的能力，同样优于公司特征值，但与A股市场不同的是，参数C的BM系数的显著性并没有相对于参数B明显下降，下一节将对AH股市场这一区别作进一步分析。最后，对比无条件CAPM和条件CAPM的AdjR2得到：条件CAPM模型优于无条件CAPM模型，其中包含投资者情绪和公司特征值条件信息（参数A）的条件CAPM模型表现最优，AdjR2仅为0199 7。

（2）无条件的FF模型与条件FF模型的对比。

在无条件的FF模型中，Size、B/M和RET的系数均不为0且显著，即H股市场上存在显著的规模效应、价值效应和动量效应，是无条件FF模型无法解释的。参数A和参数C的条件FF的Size系数t绝对值分别为1566和1571，明显低于参数B的条件FF模型对于的t值（1719），H股市场上的规模效应不再显著，说明投资者情绪可以帮助条件FF模型解释H股市场上的规模效应；与A股市场回归结果不同的是，加入投资者情绪的条件FF模型，并没有使H股的BM系数的t值明显下降，因此，投资者情绪不能帮助FF定价模型解释H股市场的价值效应。总体看，条件FF模型的AdjR2普遍低于无条件的FF模型，说明动态的FF模型预测H股市场投资组合收益率的能力优于静态的无条FF模型。

（3）单因子CAPM模型和三因子FF模型的对比。

将表3中无条件CAPM模型和无条件FF模型进行对比发现，无条件的FF模型TURN系数的t值绝对值明显下降，从1705（CAPM-UNCOND）下降到1206（FF-UNCOND），流动性效应变得不显著，表明加入SMB和HML风险因子可以捕捉H股市场上的流动性效应；条件FF模型中解释变量的t值与回归模型AdjR2均低于对应的条件CAPM模型，表明条件FF模型在捕捉H股市场股票定价异象，H股市场上预测投资组合收益率的能力优于条件CAPM模型。

（四）投资者情绪对AH股定价影响的进一步分析

通过上述回归结果分析，对比中国大陆和香港市场的投资者情绪对A股和H股定价的影响，我们得出以下结论。

1A股市场股票价格受投资者情绪影响程度大于H股

表2和表3的回归结果表明，市场投资者情绪的确是有效的条件定价信息，但其对A股和H股市场的股票定价影响程度不同，A股受投资者情绪影响较大，主要表现在：（1）将投资者情绪作为条件信息加入条件Beta参数以后，A股的规模效应从显著变得不显著，账面市值比效应显著性明显下降，而H股只有规模效应从显著变得不显著，账面市值比效应显著性没有明显的改善；（2）A股市场上，将投资者情绪作为单一条件信息比公司特征值更能够捕捉市场上存在的规模效应和价值效应，但在H股市场上，单一的投资者情绪在改善条件定价模型捕捉价值效应的能力方面，效果不明显。究其原因，主要有两点：一是A股市场个人投资者比例高于H股市场，个人投资者的投资行为主观性较强，使A股价格受情绪影响较大；二是A股市场自2010年才有卖空机制，融资融券交易门槛要求过高，导致A股市场套利套汇难度较大，同样使A股价格受投资者情绪影响较大。

本文统计了2007年至2013年上海证券交易所和香港证券交易所个人投资者和机构投资者占比情况，结果显示，上证A股的个人投资者持股账户数占比平均为9954%，持股市值平均占比8006%，远远高于相应的机构投资；而香港市场情况正好相反，机构投资者的持股账户占比平均为7058%，持股市值占比平均为7050%，均高于H股市场的个人投资者。

2A股市场非理性成分高于H股市场

从表2看到，A股市场流动性效应和动量效应在无条件和条件CAPM模型、FF模型中均呈现为显著，而表3报告的H股横截面回归的结果显示，仅无条件CAPM模型的流动性效应呈现弱显著性，其余资产定价模型中H股市场流动性效应均不显著。另外，H股市场的动量效应显著性普遍低于A股市场。因此，我们认为A股市场存在的非理性成分高于H股市场。造成该现象的原因可能是由于A股市场存在较多缺乏专业投资知识的个人投资者，非理性的个体投资者倾向于频繁交易，A股较高的换手率推高了A股的价格，从而造成流动性效应；短期内缺乏投资经验的个体投资者对市场反应不足导致A股市场存在显著的动量效应。

3投资者情绪是造成AH股价差的原因之一

由前文分析可知，市场投资者情绪可以影响股票定价，但是由于市场制度和投资者组成差异，不同市场受投资者情绪的影响不同，因此，同一家公司A股和H股，由于上市地不一样，情绪的影响程度也不一样，从而造成AH股双重上市公司同股不同价现象，主要表现在A股溢价。本文统计了2005年至2014年AH股溢价情况，近10年间，A股平均溢价率为3269%。

六、结论

本文采用Baker和Wurgler的主成分分析法分别构造了A股和H股的月度市场投资者综合情绪指数，再将投资者综合情绪指数与公司特征值（Size和B/M）作为条件信息加入条件定价模型的Beta参数中，利用Avramov和Chordia提出的两阶段回归框架，探究加入投资者情绪的条件定价模型是否能够解释股票定价异象。实证研究发现：无条件定价模型关于Beta恒定不变的假设是有误的，风险因子是随着条件信息时变的，而投资者情绪是有效的条件定价信息之一；但AH股双重上市公司由于上市地点不同，受投资者情绪的影响程度也不一样，从而造成了A股H股同股不同价现象。究其原因，该现象主要A股个人投资者比例偏高，套利套汇难度偏大，使得A股受投资者情绪影响程度大于H股。而A股市场较H股市场而言，非理性成分较高，股票异象效应更明显。因此，中国资本市场监管部门在加快中国市场化改革的过程中，应当高度重视投资者情绪对资本市场资产定价的影响，一方面进一步加强中国机构投资者建设，并加强对中国中小投资者的理性投资指导，以减少投资者非理性行为对市场的冲击；另一方面，加强A股市场的风险监控，抑制利用投资者情绪恶意投机的行为。

在本文时间序列回归结果中，仍然存在显著的条件三因子FF无法解释的风险调节收益。Pastor和Stambaugh[31]提出在FF三因子模型的基础上加入流动性风险因子，可以提高定价模型捕捉投资者组合收益率的能力。基于这种研究思路，我们可以将本文的条件资产定价模型进行改进，在FF的基础上加入流动性风险因子，甚至动量风险因子，探究多因子的条件资产定价模型对解释资本市场超额收益率，捕捉股票市场定价异象的能力。本文的研究方法给跨市场投资者情绪对交叉上市公司股票定价的影响提供了新的研究思路，此研究方法同样可以用于AB股交叉上市公司，研究A股市场投资者情绪和B股市场投资者情绪对AB股资产定价的影响。另外，美国存托凭证（ADR）一直是非美公司在美国交叉上市的主要方式，却与其基础证券价格长期存在价差，目前国内鲜少有文献对交叉上市的ADR价差进行研究。因此在后续的研究中，我们可以将本文的研究方法运用于投资者情绪对基础证券为A股基于基础证券为H股的美国ADR的定价研究，既可以帮助国内投资者和上市公司进一步认识ADR价差，也可以弥补国内关于ADR研究的缺乏。参考文献：

[1]FERNALD J，ROGERS HPuzzles in the Chinese stock market[J]Review of Economics and Statistics，2002，84：416-432

[2]FAMA EEfficient capital markets： A review of theory and empirical work[J]Journal of Finance，1970，25（2）：383-417

[3]BANZ RThe relationship between return and market value of common stock[J]Journal of Financial Economics，1981（9）：3-18

[4]CHAN K，HAMAO Y，LAKONISHOKFundamentals and stock returns in Japan[J]Journal of Finance，1991，46：1739-1764

[5]JEGADEESH N，TITMAN SReturns to buying winners and selling losers：Implications for stock market efficiency[J]Journal of Finance，1993，48：65-91

[6]BAKER M， WURGLER JInvestor sentiment and the crosssection of stock returns[J]Journal of Finance，2006，61：1645-1680

[7]AVRAMOV D，CHORDIA TAsset pricing models and financial market anomalies[J]Review of Financial Studies，2006，19：1001-1040

[8]AMIHUD Y，MENDELSON HAsset pricing and the bidask spread[J]Journal of Financial Economics，1986，17：223-249

[9]STULZ R，WASSERFALLEN WForeign equity investment restrictions， capital flight， and shareholder wealth maximization： Theory and evidence[J]Review of Financial Studies，1995，18（4）：1019-1057

[10]ALEXANDER G，EUN C，JANAKIRAMANAN SAsset pricing and dual listing on foreign capital markets：A note[J]The Journal of Finance，1987，42（1）：151-158

[11]杨中铭中国A+H股双重上市公司股价差异理论探究[J]现代商业， 2012（26）：47

[12]KAROLYI G，LI LA resolution of the chinese discount puzzle[R]Dice Center Working Paper No2003-34

[13]FAMA E，FRENCH KCommon risk factors in the returns on stocks and bonds[J]Journal of Financial Economics，1993，33：3-56

[14]De LONG J，SHLEIFER A，SUMMERS L，et alNoise trader risk in financial markets[J]Journal of Political Economy，1990，98：703-738

[15]SWAMINATHAN BTimevarying expected small firm returns and closedend fund discounts[J]Review of Financial Studies，1996（9）：845-887

[16]CHUANG W I，LEE B SAn empirical evaluation of the overconfidence hypothesis[J]Journal of Banking and Finance，2006，30：2489-2515

[17]韩立岩，伍燕然投资者情绪与IP0s之谜——抑价或者溢价[J]管理世界，2007（3）：51-61

[18]FERSON W KANDEL S，STAMBAUGH RTests of asset pricing with time varying expected risk premiums and market betas[J]. Journal of Finance，1987（42）：201-220

[19]LEWELLEN JThe timeseries relations among expected return，risk，and booktomarket[J]Journal of Financial Economics，1999，54：5-43

[20]FERSON W，HARVEY CConditioning variables and the cross section of stock returns[J]Journal of Finance，1999，54：1325-1360

[21]LETTAU M，LUDVIGSON SResurrecting the CAPM：A crosssectional test when risk premium are timevarying[J]Journal of Political Economy，2001，109：1238-1287

[22]GOMES J，KOGAN L，ZHANG LEquilibrium crosssection of returns[J]Journal of Political Economy，2003，111：693-732

[23]HO C W，HUANG C HInvestor sentiment as conditioning information in asset pricing[J]Journal of Banking and Finance，2009，33：892-903

[24]ZWEIG M EAn investor expectations stock price predictive model using closedend fund premiums[J]Journal of Finance，1973，28：67-78

[25]KALOTAY E，GRAY P，SIN SConsumer expectations and shorthorizon return predictability[J]Journal of Banking and Finance，2007，31：3102-3124

[26]BAKER M，STEIN JMarket liquidity as a sentiment indicator[J]Journal of Financial Markets2004（7）：271-299

[27]JONES CA century of stock market liquidity and trading costs[R]Working Paper， Columbia University，2001

[28]STIGLER G JPublic regulation of the securities markets[J]Journal of Business，1964，37：117-142

[29]RITTER JThe longrun performance of initial public offerings[J]Journal of Finance，199146：3-27

[30]BAKER M，WURGLER JThe equity share in new issues and aggregate stock returns[J]Journal of Finance，2000，55：2219-2257

[31]PASTOR L，STAMBAUGH RLiquidity risk and expected stock returns[J]Journal of Political Economy，2003，111：642-685

Investor sentiment and conditional assetpricing of crosslisted AH shares

MENG Weidong， ZHANG Mengyu，LU Jing

（School of Economics and Business Administration， Chongqing University， Chongqing 400044， PRChina）

Abstract：

Using principal component analysis， this paper separately constructs Ashares and Hshares composite indexes as proxy for market investor sentimentIn the twopass conditional assetpricing framework， this paper allows the Beta varying with investor sentiment and firm characteristicsThe empirical results indicate： after incorporating investor sentiments in conditional pricing models， the size effects of Ashare market and Hshare market are no longer significant； meanwhile， the B/M effect of Ashare market becomes less significantTherefore， this paper draws the conclusion that incorporating investor sentiment as conditioning information in conditional assetpricing models improves the model performance in capturing assetpricing anomalies， however， the improvement on Ashare pricing is stronger than that on Hshares， which demonstrates that different market investor sentiments have different degrees of impacts on asset pricing， resulting in the price difference of duallisted A and Hshares

Key words： investor sentiment； price difference of A and Hshare； assetpricing anomalies； conditional assetpricing model

（责任编辑傅旭东）