木薯块根拔起的最大应力数值模拟及试验

杨 望，李晓月，王蓉蓉，杨 坚，潘 琴，李娟娟

（广西大学机械工程学院，南宁 530004）

木薯块根拔起的最大应力数值模拟及试验

杨 望，李晓月，王蓉蓉，杨 坚※，潘 琴，李娟娟

（广西大学机械工程学院，南宁 530004）

为了探明木薯拔起时块根最大应力的影响规律和确定块根不被拔断的允许最大拔起力，论文采用FEM（finite element method）和SPH（smoothed particle hydrodynamics）的耦合方法及二次回归旋转设计方法，通过构建土壤－块根-茎秆系统的数值模拟计算模型，进行木薯块根拔起数值模拟试验，测定各因素组合条件下的块根最大拔起力和块根最大应力，建立块根最大应力与拔起速度、块根的大小、长短和生长深度及土壤的软硬程度的多因素耦合数学模型，研究了各影响因素及交互作用对块根最大应力的影响规律，同时，通过块根最大拔起力和块根最大应力的散点图，研究了块根最大拔起力和块根最大应力的相关性，确定了块根不被拔断的允许最大拔起力，且2014年12月底在广西武鸣县某木薯种植地，采用随机抽样方法，进行了木薯块根最大拔起力和块根拔断率的田间试验和统计分析，对块根不被拔断的允许最大拔起力进行了验证，最大拔起力小于0.98 kN时，块根拔断率为2.5%。结果表明，块根最大应力与各影响因素的多因素耦合数学模型的F检验在0.000 1水平上显著，精度较高，可用于块根最大应力的影响分析；块根最大应力随拔起速度的增大呈先增大，后减小的变化，随生长深度、块根长度和土壤硬度的增大而增大，随块根直径的增大而减小；块根最大应力与最大拔起力相关性不强，块根允许最大拔起力约为0.98 kN。

农业机械；模型；木薯块根；数值模拟试验；数学模型；最大应力；允许最大拔起力

杨 望，李晓月，王蓉蓉，杨 坚，潘 琴，李娟娟.木薯块根拔起的最大应力数值模拟及试验[J].农业工程学报，2016，32（6）：58-64.doi：10.11975/j.issn.1002-6819.2016.06.008 http://www.tcsae.org

Yang Wang,Li Xiaoyue,Wang Rongrong,Yang Jian,Pan Qin,Li Juanjuan.Numerical simulation test of maximum stress of tuber in cassava lifting[J].Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE）,2016,32(6):58－64. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2016.06.008 http://www.tcsae.org

0 引言

挖拔式木薯块根收获机械是主要的木薯块根收获机械之一，国内外学者对其进行了一定的研究，取得了一定成果。80年代德国莱比锡大学研制出了一种挖掘松土-拔起分离型的木薯块根收获机，该机采用了夹持带拔起块根，向后上方输送作业方式，功耗小，但由于块根拔起机构设计缺乏依据，块根收获损失大[1]。之后，爱沙尼亚公司在该机的基础上进行改进设计，研发出了一种Chm-3407型挖掘松土-拔起分离型的木薯块根收获机[2]。2012年廖宇兰等对挖拔式木薯收获机的挖掘铲、夹持输送机构和动力传动机构进行了设计，并对其关键参数进行了研究[3]。2000年Agbetoye等采用力学分析方法，建立了拔起土中平板的力学分析模型，对拔起力进行了分析，结果表明，预测值和实测值一致，但考虑木薯块根影响时，预测值大于实测值[4]。2011年杨望等采用物理试验、土力学分析方法，建立了木薯块根拔起力的力学模型和数学模型，对块根最大拔起力进行了预测，分析了块根最大拔起力的影响规律，结果表明，块根拔起速度对拔起力有大的影响，建立的数学模型预测精度较高[5]。2015年杨望等采用FEM（finite element method）和SPH（smoothed particle hydrodynamics）的耦合算法，建立人-茎秆-块根-土壤系统的数值模拟计算模型，研究了人的块根拔起机理[6]。2013年李娟娟采用FEM和SPH的耦合算法，建立茎秆-块根-土壤系统的数值模拟计算模型，研究了块根拔起速度和最大拔起力的关系[7]。但目前块根拔起速度、块根的生长情况和土壤的软硬程度对木薯拔起过程块根产生的最大应力值（下面简称最大应力）的影响规律及块根最大拔起力与最大应力关系的研究匮乏，机械拔起速度控制系统的设计缺乏依据。

块根生长于土中，生长情况差异性较大，通过物理试验方法较难测定木薯拔起时块根的应力变化，且在块根的拔起过程中土壤出现剪切破裂现象，因此，为了探明块根拔起速度、块根的大小、长短和生长深度及土壤的软硬程度对最大应力的影响规律，同时，为了解决田间木薯拔起收获时块根应力无法测量，导致无法准确控制木薯块根拔起速度使块根最大应力小于块根允许的最大应力，同时达到减少块根收获拔断损失和提高收获效率的难题，本文采用FEM和SPH的耦合方法及二次回归旋转设计方法，参考文献[6]给出的块根拔起数值模拟模型建模方法，构建不同条件下的土壤-块根-茎秆系统的数值模拟计算模型，进行块根拔起数值模拟试验，通过回归分析建立拔起速度、块根的大小、长短和生长深度及土壤的软硬程度与最大应力的数学模型，研究探明拔起速度、块根的大小、长短和生长深度及土壤的软硬程度对最大应力的影响规律，同时，通过研究块根最大应力和最大拔起力的关系，确定块根不被拔断允许的最大拔起力条件，为木薯块根收获机械拔起机构控制系统设计提供依据。

1 数值模拟计算模型的建立

1.1 几何模型

木薯块根的生长大多呈单层圆盘状分布，单个块根近似呈长的圆锥形，如图1a所示。SPH法要求相同材料的所有SPH节点有相同的质量，建模生成的粒子均匀分布，且有规则，这样才能提高其计算精度，因此，建模时，把单个块根简化成前部为一长方体，其余部分为一长的正四棱台，而茎秆简化成长方体，块根呈对称分布，如图1b所示，其中，短块根的最小截面的边长为最大截面边长l2的1/2，最大截面积的块根段长度l1为块根长度l的1/3，长块根的尺寸按图1b所示的比例确定。

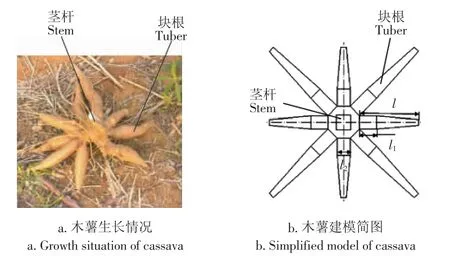
图1 木薯块根图Fig.1 Cassava tuber

块根拔起时，接近块根的土壤产生大变形和破裂，离块根较远区域的土壤产生小变形，因此，在接近块根区域的土壤（内层土壤）使用SPH，在离块根较远区域的土壤（外层土壤）使用FEM，同时，为避免边界处波的反射对求解域的影响，对外层土壤外边界（有限域表面）施加无反射边界来模拟地面。在进行数值模拟试验设计的试验时，按上述的要求及试验方案中的因素组合情况确定木薯块根实体模型的几何尺寸，分别进行建模，而土壤的建模几何尺寸根据相应的块根的长度和生长深度确定。由于实体模型对称，建模时，只建其1/4实体。

1.2 材料模型

土壤模型：土壤本构关系对块根拔起过程模拟结果有较大的影响[8-10]，因此，为了提高模拟计算精度，参照文献[11-13]，选MAT_FHWA_SOIL作土壤材料模型，MAT_ FHWA_SOIL考虑了含水率、应变软化、应变率效应、孔隙比及孔隙水压力等的影响，且服从修正的莫尔-库仑屈服准则

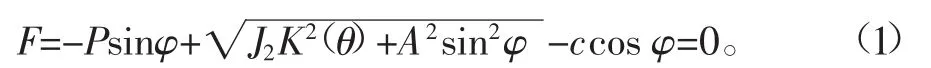
式中P为静水压力值，Pa；φ为内摩擦角，度；J2为应力偏张量第二不变量，Pa.Pa；K（θ）为张量平面角的函数；A为D-P系数；c为黏聚力，Pa。

土壤主要材料参数按文献[6]的选取，其中，土壤密度为1 880 kg/m3，内摩擦角为10.03°，黏聚力为3 kPa，含水率为15%，而土壤弹性模量及相应的体积模量和剪切模量取值根据试验设计方案确定。同时，为了易于探明各影响因素对块根最大应力的影响规律和便于建模，把块根和茎秆视作各向同性弹性材料建模，这时在数值模拟试验中，当块根的最大应力大于块根的允许最大应力[σ]（2.66 MPa）[14]时，表示相应的块根已被拔断，且块根的最大应力越大，表示块根越易被拔断。块根材料参数：密度为1 036 kg/m3，弹性模量为7.23×106Pa，泊松比为0.3。茎秆材料参数：密度为836.8kg/m3，弹性模量为35.36×106Pa，泊松比为0.3[14]。

1.3 模拟计算模型

模拟计算模型的计算精度、求解时间与网格划分疏密程度有关，网格尺寸小，仿真精度高，但求解所需时间长。本文综合考虑取内层土壤网格边长为0.008 m；外层土壤网格边长为0.01 m；木薯茎秆和块根连接处网格大小相同，边长均为0.01 m；剩余部分块根网格边长为0.02 m。网格划分方法均为扫略式。由于模型只建实体模型的1/4，因此，在定义对称边界条件时，约束对称边界网格节点的自由度，且对处于对称边界面附近的粒子用“虚粒子”处理，外层土壤外边界（除地表面）施加约束。拔起木薯的试验表明，块根拔起后靠近茎秆的块根上表面和侧面及茎秆表面始终与土壤接合，呈一个土盘，因此，靠近茎秆处的块根上表面和侧面与土壤间及茎秆与土壤间定义为固连接触，其余块根的表面与土壤间定义为点面接触，动摩擦系数取0.6，静摩擦系数取0.7。图2是建立的土壤-块根-茎秆系统耦合模拟计算模型，图3是木薯块根拔起过程的数值模拟仿真截图。

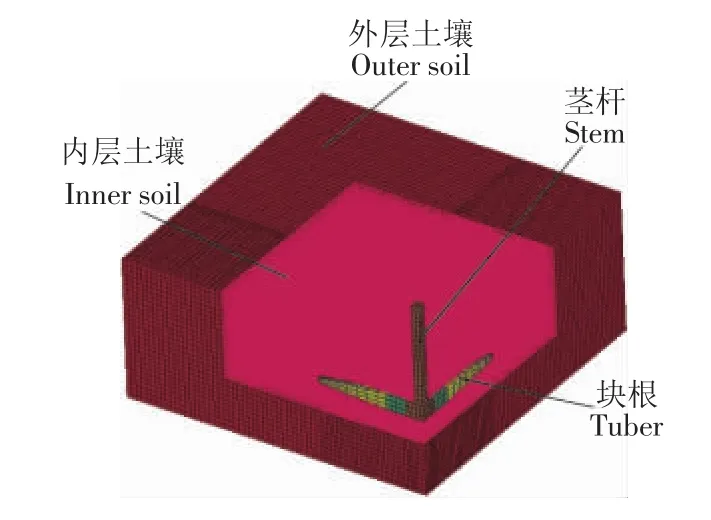
图2 块根拔起数值模拟计算模型Fig.2 Numerical calculation model of cassava lifting operation

图3 块根拔起过程的数值模拟仿真截图Fig.3 Numerical simulation of cassava tuber lifting

2 试验方案及结果

数值模拟试验采用二次回归旋转设计方法进行。选取拔起速度、生长深度、块根长度、块根直径和土壤硬度作为试验因素，块根最大应力和最大拔起力作为试验指标。由于建模时每棵木薯的块根分布形状按图1b构建，因此，本文以图1b所示短块根的长度作为块根长度因素进行模拟试验，长块根的长度由图1b所示的比例确定。而块根的直径大，其截面积大，因此，本文以图1b所示块根最大截面积处的块根截面边长作为块根直径大小的度量进行模拟试验。土壤硬度是土壤的一个综合性度量指标，由土壤的性质、弹性模量、含水率、密度等多个因素确定，且各因素的影响关系复杂，因此，为了便于建模和进行模拟试验，把对硬度值影响较大的弹性模量作为因素进行模拟试验，同时，为了获得较多的试验数据，提高回归方程的精度，增加土壤弹性模量的水平数，进行2次二次回归旋转设计试验，把试验获得的总数据进行回归分析。因素水平如表1所示。数值模拟试验方案及结果如表2所示。按表2的因素组合进行系统建模时，土壤模型的几何尺寸取值范围为：外层土壤尺寸（0.6～0.7）m×（0.6～0.7）m×（0.28～0.5）m，内层土壤的尺寸（0.412～0.6）m×（0.412～0.6）m×（0.18～0.4）m。

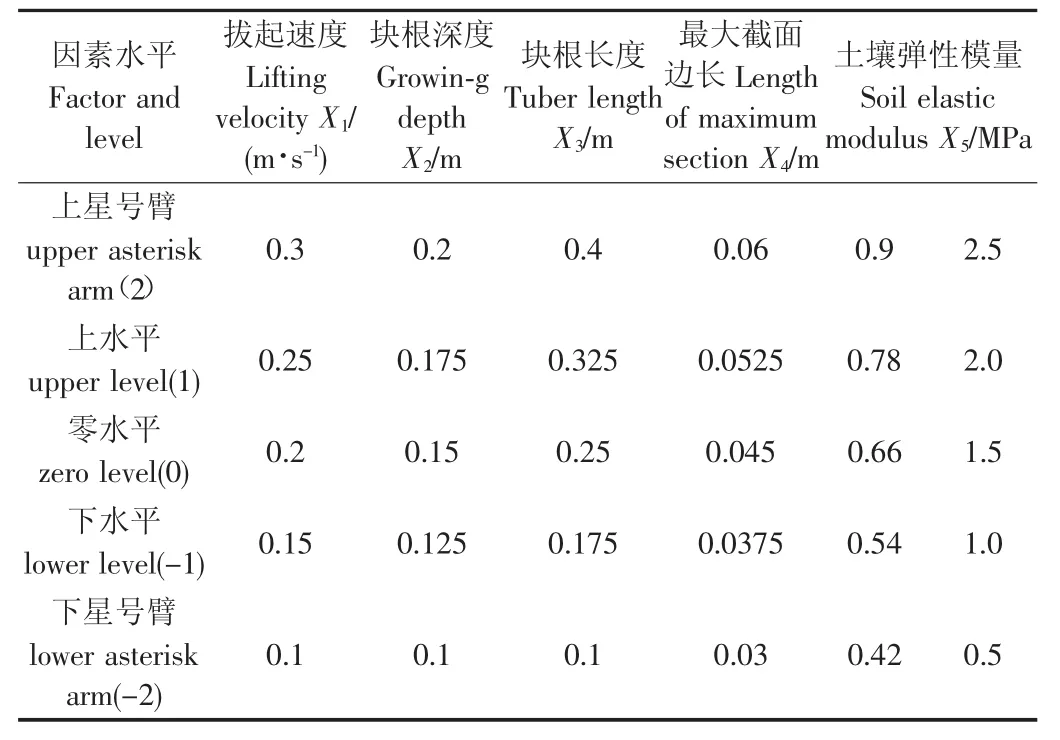
表1 多因素水平编码表Table 1 Coding table of factor and levels

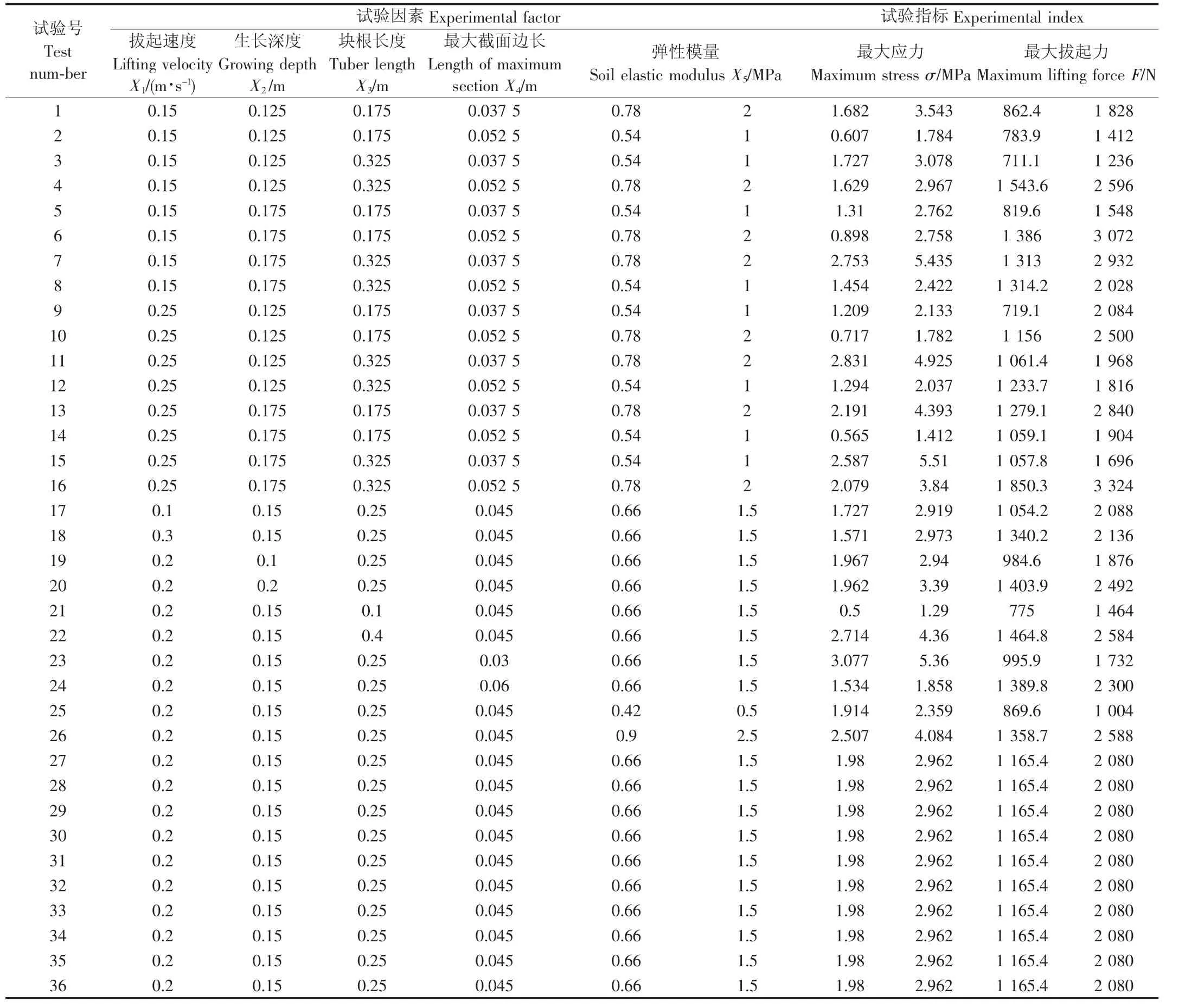
表2 数值模拟试验方案及结果Table 2 Scheme and results of simulation experiment

3 试验结果分析

3.1 回归分析

运用SPSS软件对表2的试验数据进行回归分析，得最大应力σ与拔起速度x1、生长深度x2、块根长度x3、最大截面边长x4和土壤弹性模量x5关系的数学模型为：

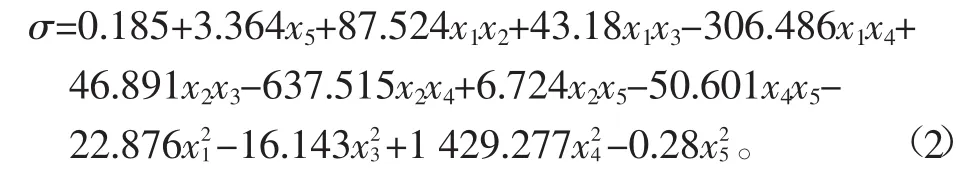
对数学模型式2和回归系数进行显著性检验，检验结果为：数学模型在0.000 1水平上显著，其回归系数也在0.06～0.001水平上显著，表明数学模型的精度较高，且拔起速度、生长深度、块根长度、最大截面边长和土壤弹性模量对最大应力有大的影响。

3.2 单因素影响

应用MathCAD软件对式2进行模拟计算，模拟计算时除考虑的因素外，其余的因素取零水平值（弹性模量取0．66 MPa），得出各因素与最大应力的关系曲线，如图4所示。

由图4a可知，最大应力σ与拔起速度x1呈凹面向下的抛物线变化，σ随x1的增大先增大，后减小。其原因是，块根拔起速度不同，块根拔起时，茎秆与块根连接处的块根的弯曲应力、剪应力大小不同，拔起速度大，弯曲应力小，但剪应力大[15]，反之相反，而块根最大应力的大小由块根弯曲应力和剪应力决定，故σ不随x1的增大而增大。由图4b、c、e可知，最大应力σ与生长深度x2成线性关系变化，而与块根长度x3和土壤弹性模量（土壤硬度）x5呈凹面向下的抛物线关系变化，σ随x2、x3和x5的增大而增大。其原因是，在上述模拟计算的条件下，x2、x3和x5增大，块根拔起时块根的弯曲变形增大，弯曲应力增大，且剪应力也增大，故σ随x2、x3和x5的增大而增大。

由图4d可知，最大应力σ随最大截面边长x4(块根的直径)的增大呈凹面向上的抛物线减小，其原因是，最大截面的边长增大，块根截面积和抗弯截面系数增大，弯曲应力减小，剪应力也小，故最大应力随最大截面边长(块根的直径)的增大而减小。

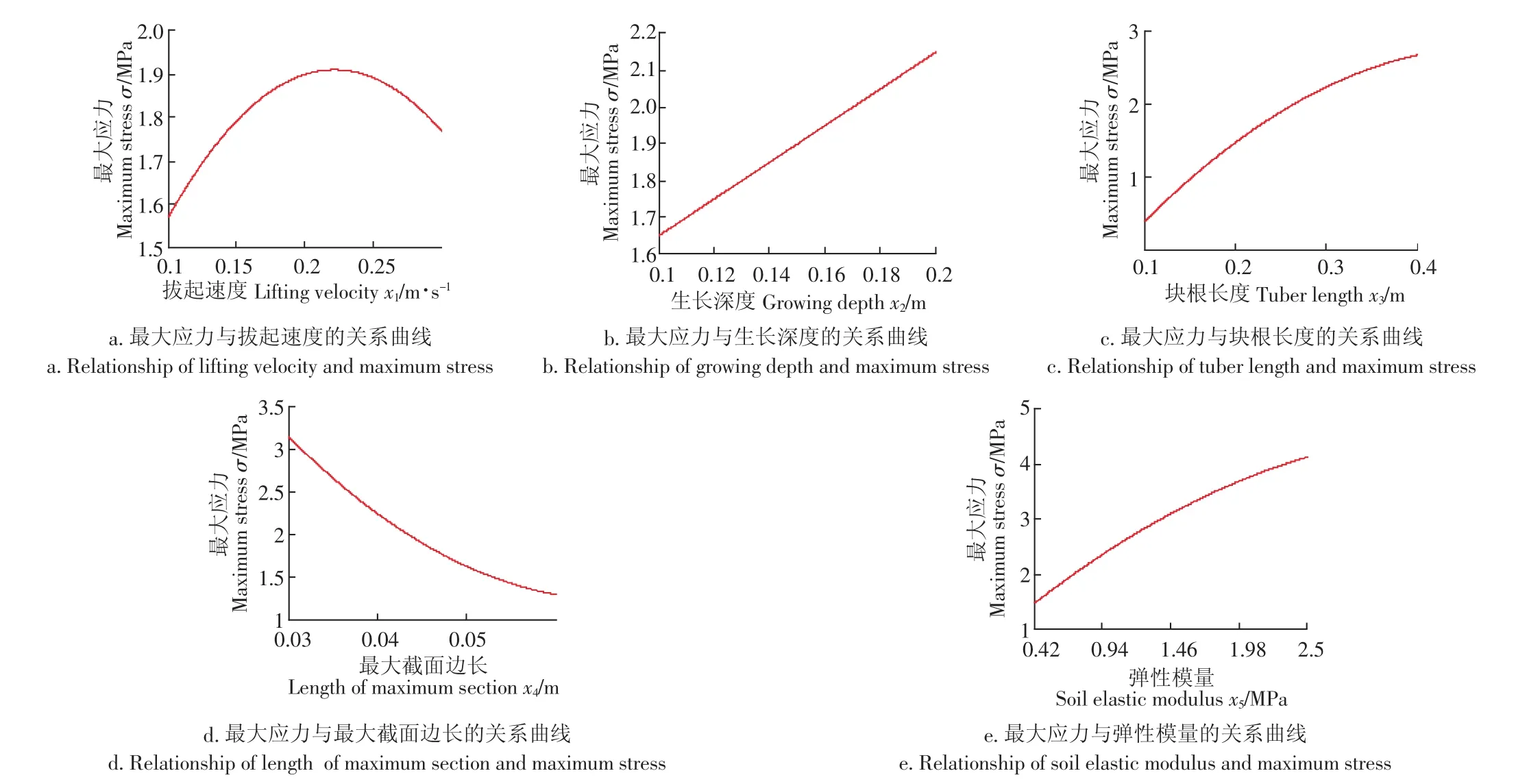
图4 影响因素与最大应力的关系曲线Fig.4 Relationship of influencing factors and maximum stress

3.3 因素交互影响

应用MathCAD软件对式2进行模拟计算，模拟计算时除考虑的因素外其余的因素取零水平值（弹性模量取0．66 MPa），得出各因素交互作用与最大应力σ的关系图，如图5所示。

由图5a可知，x1为0.3和x2为0.1组合时，σ最小，而x1为0.3和x2为0.2组合时，σ最大。x2小时，σ随x1的增大呈凹面向下的抛物线减小，但x2大时，σ随x1的增大呈凹面向下的抛物线增大。x1小时，σ随x2的增大而减小，但x1大时，σ随x2的增大而增大。

由图5b可知，x1为0.3和x3为0.1组合时，σ最小，而x1为0.3和x3为0.4组合时，σ最大。x3小时，σ随x1的增大呈凹面向下的抛物线变化，但x3大时，σ随x1的增大呈凹面向下的抛物线增大。x1小时，σ随x3的增大呈凹面向下的抛物线变化，而x1大时，σ随x3的增大呈凹面向下的抛物线增大。

由图5c可知，x1为0.3和x4为0.06组合时，σ最小，而x1为0.3和x4为0.03组合时，σ最大。σ随x1的增大呈凹面向下的抛物线变化，σ随x4的增大呈凹面向上的抛物线减小。

由图5d可知，x2为0.2和x3为0.1组合时，σ最小，而x2为0.2和x3为0.4组合时，σ最大。x3小时，σ随x2的增大而减小，而x3大时，σ随x2的增大而增大。σ随x3的增大呈凹面向下的抛物线增大。

由图5e可知，x2为0.2和x4为0.06组合时，σ最小，而x2为0.2和x4为0.03组合时，σ最大。x4小时，σ随x2的增大而增大，但x4大时，σ随x2的增大而减小。σ随x4的增大呈凹面向上的抛物线减小。

由图5f可知，x2为0.1和x5为0.42组合，σ最小，而x2为0.2和x5为2.5组合时，σ最大。σ随x2的增大而增大，随x5增大呈凹面向下的抛物线增大。

由图5g可知，x4为0.06和x5为0.42组合，σ最小，而x4为0.03和x5为2.5组合时，σ最大。σ随x4的增大呈凹面向上的抛物线减小，而σ随x5的增大呈凹面向下的抛物线增大。

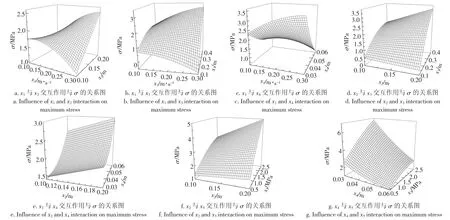
图5 因素交互作用与最大应力的关系图Fig.5 Influence of factors interaction on maximum stress

3.4 块根允许最大拔起力

图6是由表2所示的块根最大拔起力F和最大应力σ值作出的散点图。由图6可知，有些最大拔起力大，而其相应的块根最大应力较小，有些最大拔起力相对小，而其相应的块根最大应力较大，这和田间木薯块根拔起试验出现的有些块根最大拔起力大，块根未被拔断，而有些块根最大拔起力相对小，块根却被拔断的情况一致，表明最大拔起力和最大应力的相关性不强。其原因是，最大拔起力随拔起速度、块根生长深度、块根长度、块根直径和土壤硬度的增大而增大，而最大应力随拔起速度的增大呈先增大，后减小的变化，随生长深度、块根长度和土壤硬度的增大而增大，随块根直径的增大而减小。但由图6可知，当最大拔起力小于0.98 kN时，块根最大应力小于块根的允许最大应力[σ]，块根不被拔断，表明块根允许最大拔起力[F]值约为0.98kN。

图6 最大拔起力和最大应力散点图Fig.6 Scatter diagram of maximum lifting force and maximum stress

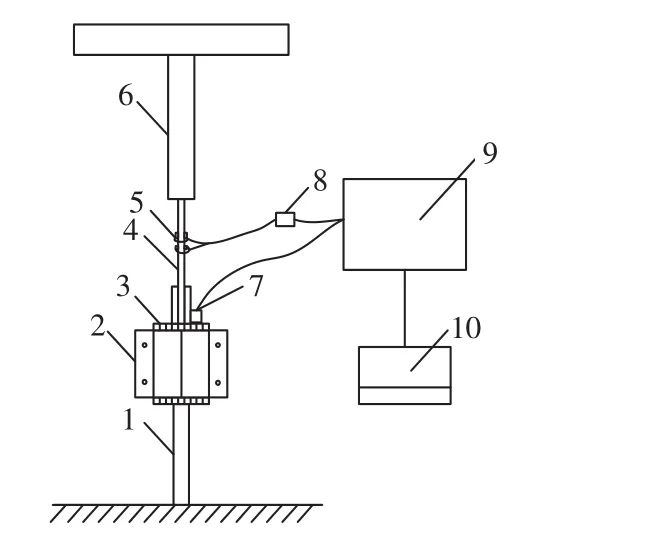
图7 木薯块根拔起力测试系统Fig.7 Sketch of measurement system for lifting force

由于木薯块根生长于土中，田间试验无法直接测量出木薯块根拔起时块根的最大应力及最大拔起力与块根最大应力的对应关系，因此，在进行块根允许最大拔起力的田间物理试验验证时，本文通过测量最大拔起力与块根拔断率的关系，间接验证数值模拟试验给出的块根允许最大拔起力的合理性。田间木薯块根拔起试验使用的主要测试设备为动态应变测试仪（型号：DH5937，江苏东华测试技术有限公司，选用采样频率为50 Hz）和土壤硬度计（型号：TYD-1，杭州托普仪器有限公司）。试验时间：2014年12月底。试验地为广西武鸣县某木薯种植地(中国最大的木薯种植基地)，土质为红黏土，土壤硬度平均值为4.84 kg/cm2。木薯品种：华南205（收获期）。木薯块根拔起力测试系统如图7所示，试验现场如图8所示。田间试验时共随机选择134棵木薯（共计1 344个块根）进行拔起试验。田间木薯拔起的最大拔起力F和块根拔断率η的试验结果统计表如表3所示。由表3和试验中木薯块根拔起过程的观察可知，当最大拔起力小于0.98 kN时，虽然在被拔起的木薯块根中还存在少量块根由于直径过小，长度过长，而被拔断，但块根拔断率较小，为2.5%，表明以0.98 kN作为块根允许最大拔起力[F]合理，且在设计木薯块根拔起机构控制系统时，应控制拔起速度，使块根拔起力小于块根允许最大拔起力[F]，使块根拔断收获损失减少。

图8 田间试验现场图Fig.8 Test on field

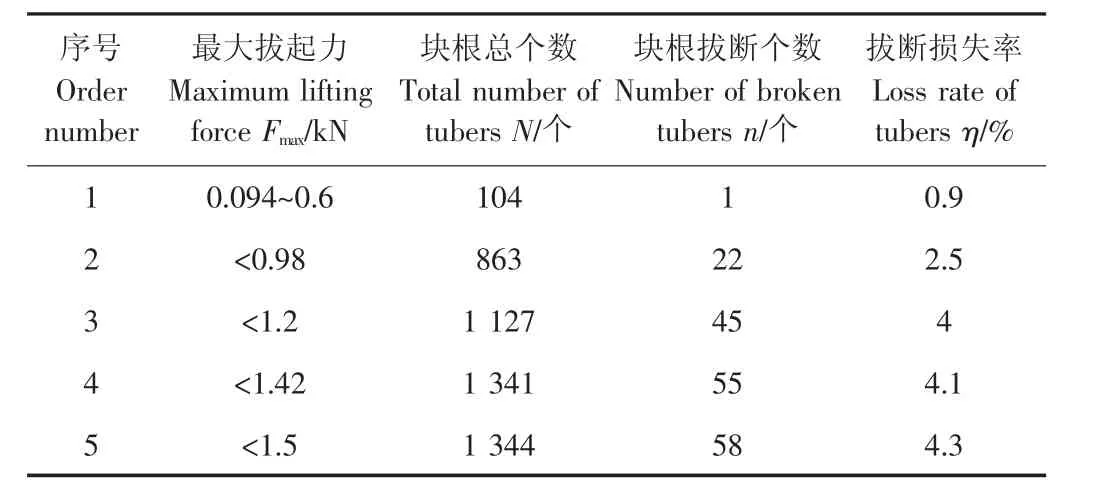
表3 最大拔起力和块根拔断率统计表Table 3 Statistical list of maximum lifting force and breaking rate of tuber

4 结论

1）建立的最大应力与拔起速度、块根生长深度、块根长度、最大截面边长和土壤弹性模量的数学模型精度较高，可用于最大应力的影响规律分析，且拔起速度、块根生长深度、块根长度、块根直径和土壤硬度对最大应力有大的影响。

2）最大应力随拔起速度的增大呈先增大，后减小的变化，而随生长深度、块根长度和土壤硬度的增大而增大，随块根直径的增大而减小。

3）拔起速度x1为0．3与块根深度x2和块根长度x3为0．1及块根深度x2为0.2与块根长度x3为0.1和最大截面边长x4为0.06组合时，因素交互作用下的块根最大应力σ分别获得相应的最小值，而x1为0.3与x2为0.2和x3为0.4及x2为0.2与x3为0.4和x4为0.03组合时，σ分别获得相应的最大值。

4）最大应力和最大拔起力相关性不强，块根允许最大拔起力约为0.98 kN。在设计木薯块根拔起机构控制系统时，应控制块根拔起速度，使块根拔起力小于块根允许最大拔起力，减小块根拔断收获损失。

[1]Agbetoye L A S.Developments in cassava harvesting mechanization [J].West Indian Journal of Engineering,1999,22(1):11-19.

[2]Strengthening the competitiveness and eco-efficiency of SMEs in Thailand:market assessment of mechanization potential for cassava production.Bangkok:AgriSource Co.Ltd,007.

[3]Liao yulan,Sun Youpan,Liu shihao,et al.Development and prototype trial of digging-pulling style cassava harvester[J]. Transactions of the Chinese Society of Agricultural Engineering（Transactions of the CSAE）,2012,28(Suppl.2):29-35.

[4]Agbetoye L A S,Dyson J,Kilgour J.Prediction of the lifting forces for cassava harvesting[J].Journal of Agricultural Engineering Research,2000,75(1):39-48.

[5] 杨望，蔡敢为，杨坚，等.木薯块根拔起力的力学模型和数学模型分析[J].农业工程学报，2011，27(11)：95－100. Yang Wang,Cai Ganwei,Yang Jian,et al.Mechanical and mathematical model analysis of uprooted force on cassava storage root[J].Transactions of the Chinese Society of Agricultural Engineering（Transactions of the CSAE）,2011,27(11):95－100. (in Chinese with English abstract)

[6]Yang Wang,Li Juanjuan,Yang Jian,et al.Numerical simulation of an experienced farmer lifting tubers of cassava for designing a bionic harvester[J].CMES:Computer Modeling in Engineering and Sciences,2015,104(6):471-491.

[7] 李娟娟.木薯收获机械拔起速度模型的优化研究[D].南宁：广西大学，2013. Li Juanjuan.The Optimization Study of the Cassava Harvest MachineryUprootedVelocityModel[D].Nanning:GuangxiUniversity, 2013.

[8] 钟江，蒋建东，姜涛.基于光滑粒子流体动力学仿真的板结土壤深旋耕技术[J].机械工程学报，2010，46(19)：63-69. Zhong Jiang,Jiang Jiandong,Jiang Tao.Deep-tillage rotavator technology based on smoothed particle hydrodynamics simulation[J].Journal of Mechanical Engineering,2010,46(19): 63-69.(in Chinese with English abstract)

[9]Lewis B A.Manual for LS-DYNA soil material model 147[R]. Department of Transportation:Federal Highway Administration, 2004.

[10]丁峻宏，金先龙，郭毅之，等.土壤切削大变形的三维数值仿真[J].农业机械学报，2007，38(4)：118－121. Ding Junhong,Jin Xianlong,Guo Yizhi,et al.Study on 3-D umerical simulation for soil cutting with large deformation[J]. Transactions of the Chinese Society for Agricultural,Machinery, 2007,38(4):118－121.(in Chinese with English abstract)

[11]顿国强，陈海涛，李昂，等.刀齿排布旋向对免耕覆秸精播机清秸单体性能的影响[J].农业工程学报，2015，31(12)：48－56. Dun Guoqiang,Chen Haitao,Li Ang,et al.Effect of rotation direction of knife teeth configuration on clearing straw unit performance for no-tillage and straw mulching precision seeder [J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE),2015,31(12):48－56.(in Chinese with English abstract)

[12]齐龙，梁仲维，马旭，等.耙压式除草轮与水田土壤作用的流固耦合仿真分析及验证[J].农业工程学报，2015，31(5)：29－37. Qi Long,Liang Zhongwei,Ma Xu,et al.Validation and analysis of fluid-structure interaction between rotary harrow weeding roll and paddy soil[J].Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE),2015,31 (5):29－37.(in Chinese with English abstract)

[13]杨望，杨坚，贾丰云，等.种植于红粘土的木薯块根挖掘作业数值模拟[J].机械工程学报，2013，49（9）：135-143. Yang Wang,Yang Jian,Jia Fengyun,et al.Numerical simulation of digging operation of cassava root planted in red clay[J]. Journal of Mechanical Engineering,2013,49(9):135-143.(in Chinese with English abstract)

[14]杨望，杨坚，郑晓婷，等.木薯力学特性测试[J].农业工程学报，2011，27(增刊2)：50-54. Yang Wang,Yang Jian,Zheng Xiaoting,et al.Experiment on mechanical properties of cassava[J].Transactions of the Chinese Society of Agricultural Engineering（Transactions of the CSAE）, 2011,27(Suppl.2):50-54.(in Chinese with English abstract)

[15]杨望，蔡敢为，杨坚.土壤直剪试验的动力学仿真[J].农业机械学报，2011，42(7)：96－101. Yang Wang,Cai Ganwei,Yang Jian.Dynamics simulation of direct shear test[J].Transactions of the Chinese Society for Agricultural Machinery,2011,42(7):96－101.(in Chinese with English abstract)

Numerical simulation test of maximum stress of tuber in cassava lifting

Yang Wang,Li Xiaoyue,Wang Rongrong,Yang Jian※,Pan Qin,Li Juanjuan
(College of Mechanical Engineering,Guangxi University,Nanning 530004,China)

In order to discover the influence law of maximum stress of cassava tuber,and obtain the allowable maximum lifting force without the breakage of cassava tuber during cassava tuber lifting,the numerical simulation model of soil, cassava tuber and cassava stem system was established by adopting explicit dynamics simulation software LS-DYNA.In the numerical simulation model,large deformations and fractures of the soils close to the tubers occurred and small deformations occurred in most parts of the rest.Thus,the coupling method of FEM(finite element method)and SPH (smoothed particle hydrodynamics)was applied in the numerical simulation model.The SPH method was used in inner soil layer where large deformations occurred and the FEM method was used in the outer soil layer where small deformations occurred.The coupling between the inner and outer soil was realized by“nodes-surface”in LS-DYNA.And MAT_FHWA_SOIL was selected as soil material model in the numerical simulation model,because it takes account of the influence of moisture content,strain softening,strain rate effect,void ratio,and pore-water pressure,and obeys the modified Mohr-Coulomb yield criterion.Numerical simulation tests of cassava tuber lifting were carried out by using the numerical simulation model and the quadratic regression rotation design method.There were 5 experiment factors and 2 experiment indices in the quadratic regression rotation design tests.The experiment factors were the lifting velocity,the length, dimension and growth depth of the tuber and the soil hardness,respectively.The experiment indices were the maximum lifting force and the maximum stress of tuber which were measured under different factor combination conditions.According to the numerical simulation tests results,the multi-factor coupling mathematic models between the maximum stress of the tuber and the lifting velocity,the length,dimension and growth depth of the tuber and the soil hardness were established by using statistical software SPSS.Based on the coupling mathematic models,the different influencing factors and their interactions on the maximum stress of the tuber were investigated,the relationship curves were drawn by using mathematics software MathCAD,and the corresponding influence laws were obtained by the relationship curves.And based on the numerical simulation tests results,the scatter diagram of the maximum lifting force and the maximum stress of tuber was plotted by using mathematics software MathCAD,and the correlation between them was studied by the scatter diagram. According to the scatter diagram,the allowable maximum lifting force was obtained under which there was no breakage of tuber.Moreover,the allowable maximum lifting force under which there was no breakage of tuber was verified by cassava tuber lifting tests,which were carried out in the cassava planting field in Wuming County,Guangxi Zhuang Autonomous Region in the end of December 2014 by adopting the method of random sampling.Meanwhile,the maximum lifting force and the breakage rate of tuber were analyzed by statistical method.When the allowable maximum lifting force was less than 0.98 kN,the breakage rate of tuber was 2.5%.The result showed that the multi-factor coupling mathematic models between the maximum stress of the tuber and the lifting velocity,the dimension and growing depth of the tuber and the soil hardness had high precision,because the F test of the multi-factor coupling mathematic models was significant at 0.000 1 level.The multi-factor coupling mathematic models could be used in the effect analysis of the maximum stress of tuber.With the increasing of lifting velocity,the maximum stress of tuber increased at first and then decreased.With the increasing of growing depth,tuber length and soil hardness,the maximum stress of tuber increased.But the maximum stress of tuber decreased when tuber′s diameter increased.There was little correlation between the maximum stress of tuber and the allowable maximum lifting force.The allowable maximum lifting force was 0.98 kN.

agricultural machinery;models;cassava tuber;numerical simulation test;mathematics model;maximum stress; allowable maximum lifting force

10.11975/j.issn.1002-6819.2016.06.008

S225.7+1

A

1002-6819（2016）-06-0058-07

2015-10-09

2016-01-27

国家自然科学基金项目（51365005）；国家自然科学基金项目（51065003）；广西制造系统与制造技术重点实验室课题（13－051－09S01）；广西研究生教育创新计划资助项目（YCSZ2015040）

杨 望，男，广西合浦人，副教授，博士，硕士生导师，主要从事木薯和甘蔗收获机械设计基础理论研究。南宁 广西大学机械工程学院，530004。Email：yanghope@163.com

※通信作者：杨 坚，男，广西合浦人，教授，主要从事农业机械设计及性能优化研究。南宁 广西大学机械工程学院，530004。

Email：yangokok@gxu.edu.cn

中国农业工程学会高级会员：杨 望（E041200798S）