采用结构进化策略的Lagrange乘子法优化换热网络

张春伟，崔国民，陈上，陶佳男（上海理工大学新能源科学与工程研究所，上海 200093）



采用结构进化策略的Lagrange乘子法优化换热网络

张春伟，崔国民，陈上，陶佳男
（上海理工大学新能源科学与工程研究所，上海 200093）

摘要：针对罚函数法处理有约束问题时存在的不足，采用Lagrange乘子法优化换热网络。为求解Lagrange函数方程组，根据确定性方法，提出最速下降法求解策略以及Powell法求解策略。通过极小值判断机制，保证Lagrange函数方程组的解是原换热网络目标函数值的极小值。根据实际工况，提出结构进化策略，与Lagrange乘子法相结合，实现了换热网络全局最优化。通过经典算例验证了两种求解策略的有效性、准确性以及结构进化策略的通用性。与文献结果进行对比，结果表明本算法具有较强的局部搜索能力以及全局搜索能力，能够找到更优的换热网络结构，有利于在工业生产中节约成本。

关键词：换热网络；Lagrange乘子法；最速下降法；Powell法；结构进化策略

第一作者：张春伟（1992—），男，硕士研究生，从事过程系统优化研究。联系人：崔国民，教授，博士生导师。E-mail cgm1226@163.com。

换热网络综合（heat exchanger network synthesis，HENS）是系统工程中的一个重要组成部分，其目的在于提升系统的回收能力和经济性。换热网络中存在表示换热器有无的0-1整型变量以及表示热负荷分布的连续变量，所以换热网络综合属于混合整数非线性规划（mixed integer nonlinearprogramming，MINLP）范畴[1]。此外，FURMAN 等[2]证明其为NP-难问题，因此即使小规模的换热网络问题也不能证实找到全局最优解[3]。

换热网络综合方法主要可分为以Linnhoff为代表的夹点设计法[4]和以Grossmann为代表的数学规划法[5]两大类。夹点设计法将换热网络综合问题分解为两个子问题，分别对其优化后，能够得到一个较好的换热网络设计。数学规划法首先将换热网络综合问题转化为有约束的多变量数学模型，然后采用优化算法对该模型进行求解以得到最优的换热网络结构。在换热网络研究中，为处理有约束问题，常借助罚函数法将其转化为无约束问题，进而用无约束最优化方法求解[6]。

罚函数法操作简单，使用方便，并能求解导数不存在的问题。但其存在着一个固有的缺点，即当罚因子趋向极限时，罚函数的Hessian矩阵条件数无限增大，呈病态现象，直接影响算法的精度与收敛性，给罚函数的极小化增加困难；但当罚因子取值很小时，罚函数的极小点会远离约束问题的最优解，计算效率很差，所以罚因子的取值问题采用是罚函数法时存在的实质性困难[7]。

Lagrange乘子法通过求解一系列无约束优化问题，间接得到原问题的最优解，是另一种常用的处理有约束问题的方法[8-9]。Lagrange乘子将约束条件与原目标函数结合构造Lagrange函数，令其各个变量的一阶偏导数为零，得到与变量个数相等的等式方程组。通过求解该方程组，得到原目标函数极值。由于不含罚因子，所以在处理有约束问题时，Lagrange乘子法能够克服罚函数法的不足。且计算经验表明，相比罚函数法，Lagrange乘子法的性能更加优越，收敛速度也相对较快[8]。所以Lagrange乘子法引起了人们广泛的研究和关注，在系统优化[10-11]、参数辨识[12]、实际工程[13-14]中均得到了应用。

鉴于此，本文采用Lagrange乘子法处理有约束的换热网络综合问题。为求解方程组，提出最速下降法（steepest descent method，SD）求解策略以及Powell法（Powell method，Powell）求解策略，并通过极小值判断机制剔除非函数极小值的解。对于换热网络MINLP问题，Lagrange乘子法只能收敛于局部极值，所以结合实际工况，提出结构进化策略（structure evolution，SE），使原有的结构不断进化，获得更优的换热网络设计，跳出局部最优解，进而实现换热网络的全局最优化。最后通过经典算例对两种求解策略以及结构进化策略进行验证。

1　换热网络数学模型及其Lagrange函数

1.1换热网络问题数学描述

换热网络综合问题可表述如下：现有NH股热流体、NC股冷流体，分别需要冷却、加热到目标温度。在冷、热流体之间设置多个换热器，实现能量回收，进而形成换热网络。当某一股流体未达到目标温度时，为其匹配冷或热公用工程。过程流体和公用工程的热容流率、进出口温度以及换热器换热系数均已知。以年综合费用为优化目标，包括运行费用和投资费用两部分，运行费用为消耗冷、热公用工程时产生的费用，投资费用为设置换热器时产生的费用，可分为面积费用和固定投资费用。本文采用GROSSMANN等[5]提出的无分流分级超结构模型，其中，换热网络的级数为换热器的最大个数为。现以2股热流体和2股冷流体为例表述分级超结构模型，如图1所示。

1.2优化的目标函数

针对上述换热网络模型，以年最小年综合费用为优化目标，其数学函数为式(1)。

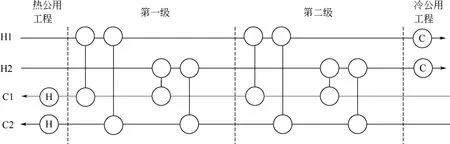
图1　换热网络无分流的分级超结构

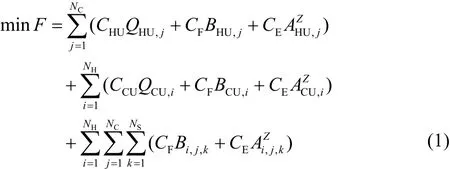
式中，B为0-1整型变量，表示换热器有无，当换热器存在时B=1，反之则B=0；CCU、CHU分别为冷、热公用工程的费用系数；CF为设置换热器时的固定投资费用；CE为面积费用系数；Z为面积费用指数；QHU,j、QCU,i分别为热公用工程与冷流体之间的换热量和冷公用工程与热流体之间的换热量；AHU,j、ACU,i分别为其相应换热器的面积；Ai,j,k为冷热流体之间换热器面积。本文以单个换热器的换热量Qi,j,k为优化变量，各换热器均采用逆流传热方式，见式(2)～式(4)。

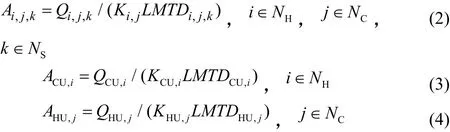
式中，Ki, j、KCU,i、KHU, j为热流股与冷流股匹配的总传热系数，Ki, j计算公式如式(5)。

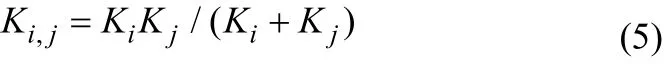
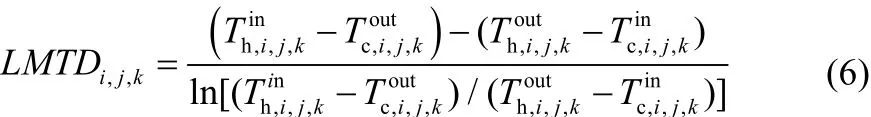
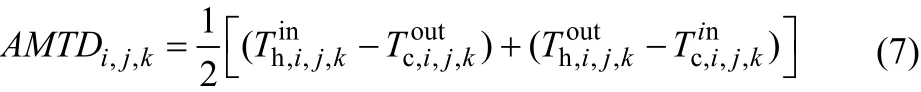
1.3主要约束条件

根据换热网络数学描述以及文献[15]可知，目标函数的主要约束条件如式(8)～式(29)所示。

（1）流体目标温度约束

（2）单股流体热平衡

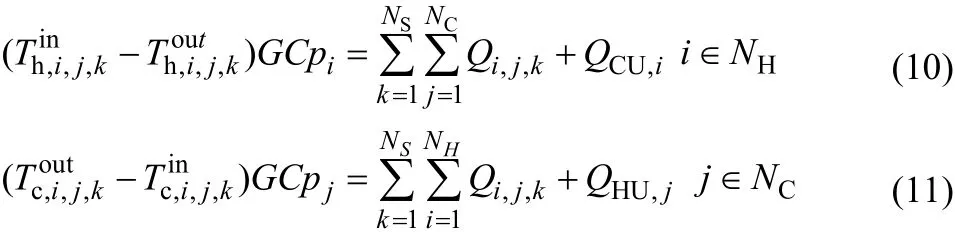
（3）冷热公用工程热平衡

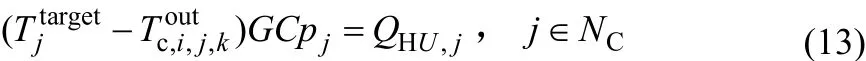
（4）换热器热平衡

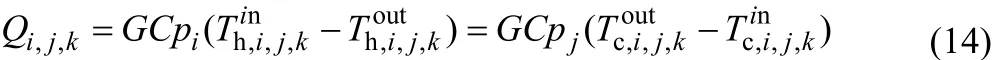
（5）可行温度约束

（6）非负约束

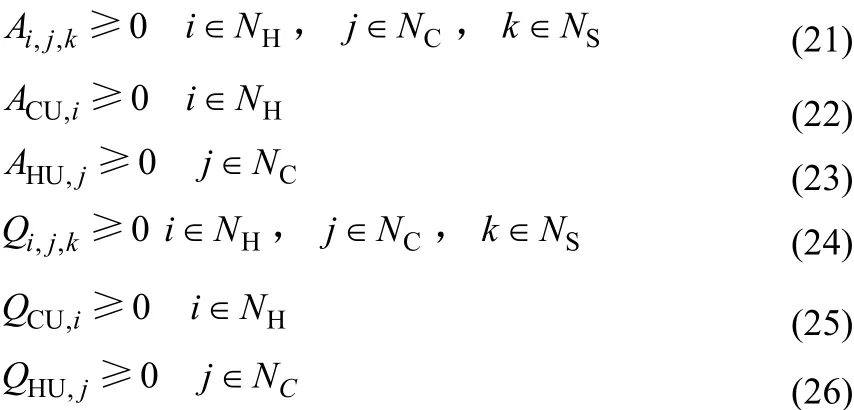
（7）逻辑约束

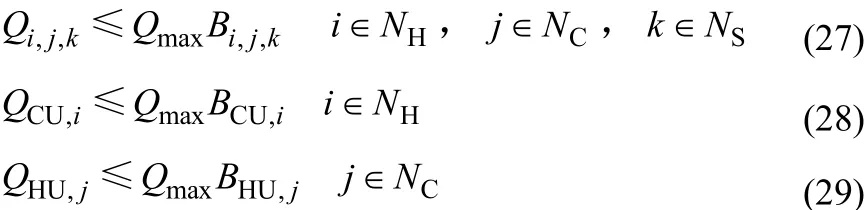
1.4换热网络的Lagrange函数

由换热网络数学描述可知，模型中的主要约束条件为温度约束，即当流体出口温度等于目标温度时，其他约束条件也能够满足。所以本文通过Lagrange乘子将温度约束与原目标函数结合，构造Lagrange函数，函数无任何约束。其形式如式(30)。

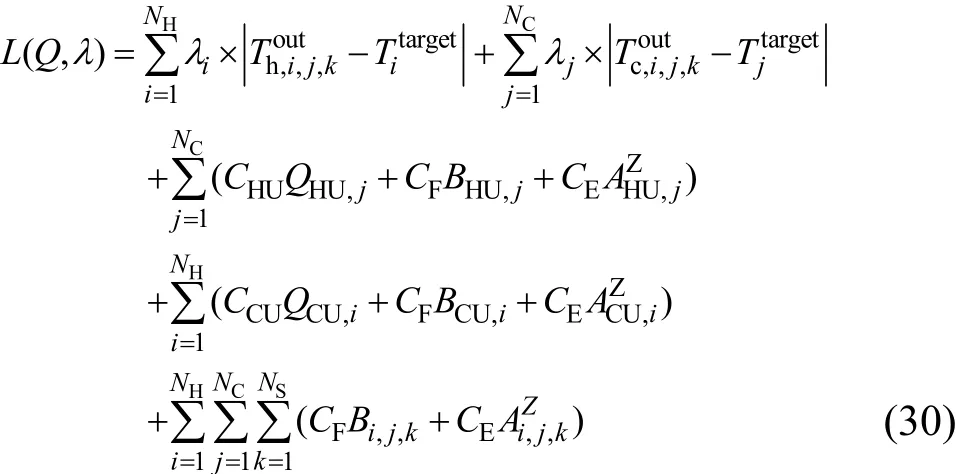
对Lagrange函数的各个变量求导，令其为零，可以得到Lagrange函数方程组，其形式如式(31)。

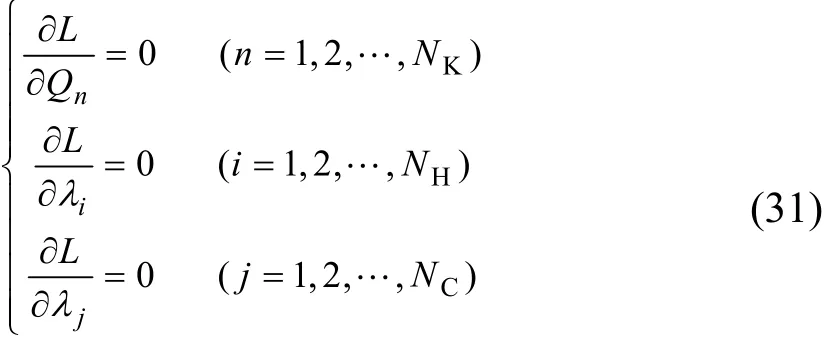
式中，NK为当前换热器个数，最大值为。Lagrange乘子将一个具有NK个变量与个约束的问题转化为更容易求解的个方程组，而目标函数的极小值点也对应着此方程组的一组解。

2　两种基于确定性方法的求解策略

采用Lagrange乘子法解决换热网络综合问题，首先将有约束的目标函数转化为无约束Lagrange函数，并通过求解方程组来获得原函数的极小值[16]。但在数值计算过程中，Lagrange函数对某一变量的偏导数为具体的数值，而非方程组形式，所以在计算时不能直接采用数值解法求解方程组。鉴于此，本文结合确定性方法提出了两种求解策略，达到间接求解方程组的目的，并通过极小值判断机制对方程组的解进行验证。

2.1极小值判断机制

满足极值点的一阶必要条件的Lagrange乘子虽然必定存在，但考虑到目标函数严重的非线性和非凸特性，满足方程组即一阶必要条件的解可能为鞍点或拐点，而非极值点，所以引入极值点的二阶必要条件作为函数收敛的判断机制。

对方程组求解后，继续计算此解所对应位置的Lagrange函数二阶导数，判断其Hessian矩阵是否正定。如果Hessian矩阵正定，则此解为Lagrange函数的极小值。反之，则不为Lagrange函数的极小值，此时随机产生新的初始解，使算法继续搜索，直到找到函数的极小值。

2.2最速下降法求解策略

根据公式(31)可知，每一个变量所对应的一阶偏导数值为零时，方程组得解。据此，可根据最速下降法思想，在迭代计算中，以每次求得的偏导数值为基础，沿其负梯度方向进行一维搜索，从而确定其搜索方向以及最佳搜索步长，直到各个变量的一阶偏导数值近似为零。

算法的终止条件为变量的对应梯度Dk的范数小于等于设定的常数阈值，即。满足此终止条件时，各个变量的一阶偏导数值近似为零，方程组也得到了相应的解。算法求解步骤如下。

Step1设置初始参数，常数阈值e1。

Step2计算目标函数的一阶导数，并确定Lagrange函数最速下降方向Step3计算最速下降方向Dk的范数，如果，转Step 6，否则转Step 4。

Step4沿最速下降方向Dk进行一维搜索，确定搜索步长αk。

Step5通过式(32)、式(33)更新换热量以及拉格朗日乘子。

变量更新后，转Step 2。

Step6通过极小值判断机制验证当前解，如果为极小值，则迭代结束；否则随机产生新初始解，转Step 2。

2.3Powell法求解策略

Powell法是一种求解无约束最优化问题的直接搜索法[17]，其本质是共轭方向法。由于对方程组求解的最终结果是各个变量的一阶偏导数为零，所以可以构造新的目标函数间接求解方程组。函数形式如式(34)。

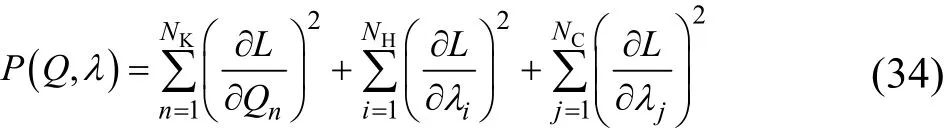
Step1确定变量维数N，设置初始点X0（包含换热量Q以及Lagrange乘子），收敛精度，一组线性无关的方向，Di取N个坐标轴的方向，即N阶单位矩阵，其中N的最大取值为

Step2从初始点X0依次沿方向进行一维搜索，确定每次迭代的步长，得到X1，X2，··，XN，即式(35)、式(36)。

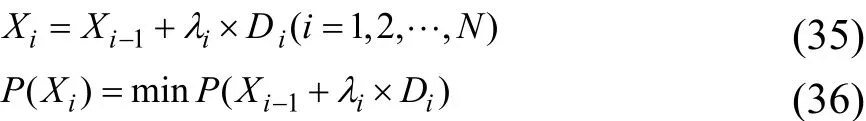
Step3判断迭代计算是否结束：若满足下式，则得到解XN，转Step 8，否则转Step 4，如式(37)。

Step5引进第(N+ 1)个搜索方向和新的点Xt，如式(39)、式(40)。

方向替换判断，如式(41)、式(42)。

①若满足

则将XN作为新的初始点，沿原方向搜索，即转Step 2。

②若满足

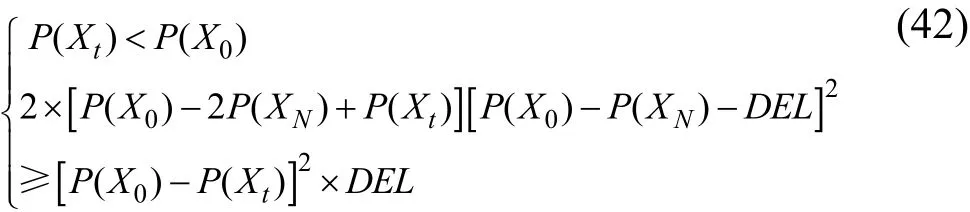
则将XN作为新的初始点，沿原方向搜索，即转Step 2。

③若以上两条件均不满足，则转Step 7。

Step7以XN作为起始点，沿方向DN1+进行一维搜索，并得到此方向上的极小值点XN1+。将方向用新的方向DN1+替换，产生一组新的方向，以XN1+作为新的初始点，转Step2。

Step8通过极小值判断机制验证解XN，如果为极小值，则迭代结束；否则随机产生新的初始解，转Step2。

3　结构进化策略

换热网络综合问题严重的非凸、非线性，导致Lagrange乘子法只能收敛于求解域内的局部最优解。所以为实现换热网络的全局最优化，本文结合换热网络实际工况，提出了一种优化整型变量的结构进化策略。考虑到换热网络问题均存在全局最优解，其对应结构的换热器个数也为定值，但对现在的研究成果而言，最优结构和最优换热器个数均无法确定。此外，换热器之间具有很强的关联性，同一股流体中的上游换热器的位置和换热量直接影响下游换热器。所以如果在原结构基础上仅仅增加或减少一个换热器，并以此新结构对应的目标函数值变化作为此操作是否成功的标准，则很有可能使换热网络结构的生成方向偏离最优结构。本文以此为出发点，根据相关文献中算例的优化结构和实际工况设定换热器个数范围，减小换热器相互组合的可能性，调控结构的进化方向，增强算法的局部最优解跳出能力，提高搜索效率。结构进化策略主要包括结构进化、结构判断、结构选择等部分，各部分操作如下所示。

（2）结构进化 为增加随机性，通过构造进化概率函数决定对当前结构采取何种操作。其具体形式如式（43）。

其中常数c用来调整当前结构换热器生成或消去的概率。确定结构中的换热器个数N后，调用随机数rand，若，则对其执行换热器生成操作，否则执行换热器消去操作。

①换热器生成操作。在整个分级超结构中随机选择Ng个位置作为换热器生成位置，分别将其与原结构中的换热器进行对比，如果发生位置重合，则在此位置保留原结构中的换热器及其换热量；反之，则在原结构该位置上添加换热器，并赋值换热量，令其，生成新的换热网络结构后。使用Lagrange乘子法对其优化。其中

②换热器消去操作。在整个分级超结构中随机选择Ne个位置作为换热器消去位置，分别将其与原结构中的换热器位置进行对比，如果发生位置重合，则将原结构中的此位置换热器消去，否则保留原结构中的换热器，生成新结构后，使用Lagrange乘子法对新结构优化。其中

其中，Ng、Ne的定义方式可以保证进化后得到的新结构换热器个数均在设定的范围内。

（3）结构判断 由于结构进化操作具有随机性，所以为提高进化效率，排除不合理结构，本文提出两条结构判断公式，即对流体上的换热器个数进行限制和判断。执行进化操作后，分别计算冷、热流体上的换热器个数，当满足判断公式时，使用Lagrange乘子法对新结构优化；否则认为结构进化操作无效，重新执行。结构判断公式如式(44)、式(45)所示。

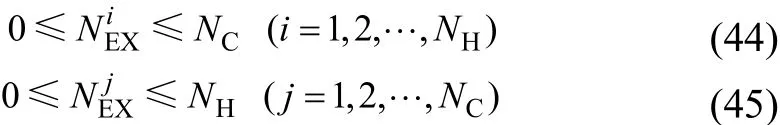
（4）结构选择 新结构产生后，若其费用值较原结构下降，则将原结构更新，否则以一定的概率接受新结构。选择概率函数形式如式(46)所示。

4　算例分析

引用文献[18-19]的算例对算法进行验证，构造Lagrange函数方程组后，分别采用两种求解策略对其求解，并对结果进行分析。然后对两结果对应的换热网络结构执行结构进化策略，验证其有效性及准确性。过程流体由4股热流体和5股冷流体组成，相关参数如表1所示。换热器费用计算公式，热公用工程为热油，费用为6$/(kW× a)，冷公用工程为冷水，费用为6$/(kW× a)。

在迭代步数等参数设置相同的情况下分别采用两种求解策略对算例进行优化，图2为最速下降法求解策略优化结果的流股匹配图，其对应的年综合费用为2941949$/ a。图3为Powell法求解策略优化结果的流股匹配图，其对应的年综合费用为2942153$/ a。

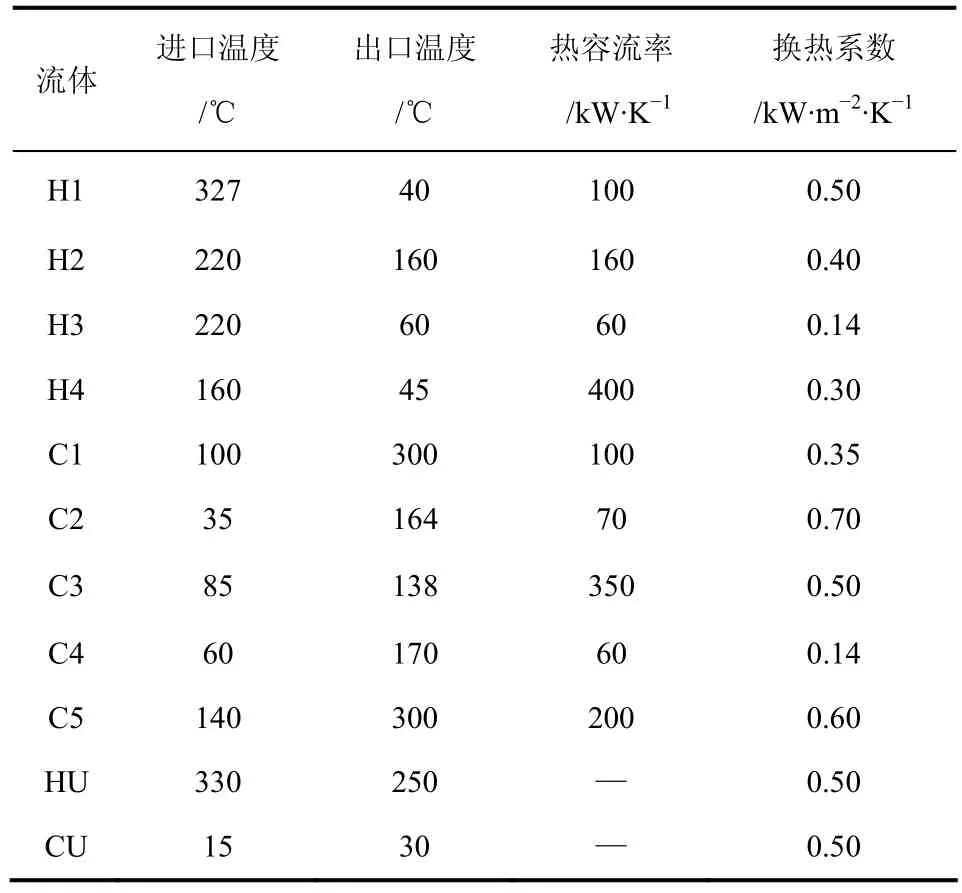
表1　算例流股参数

通过对比两结构图可以发现，图2所示的换热网络结构较图3在第二级多出一个换热器，但此换热器可与第一级相同位置的换热器叠加，而且不会引起其他变量的变化。叠加后的换热网络结构与图3相同，而连续变量的差别可认为由精度差异或极小值判断机制造成。可以证明Lagrange乘子法能够有效处理多约束的换热网络综合问题，并在初始条件相同的情况下，两种求解策略能够得到近似相同的结果。对比两者的年综合费用值可知，最速下降法求解策略的结果相对较优，这是因为Powell法求解策略构造的函数光滑性要比Lagrange函数差，进而影响了优化结果。

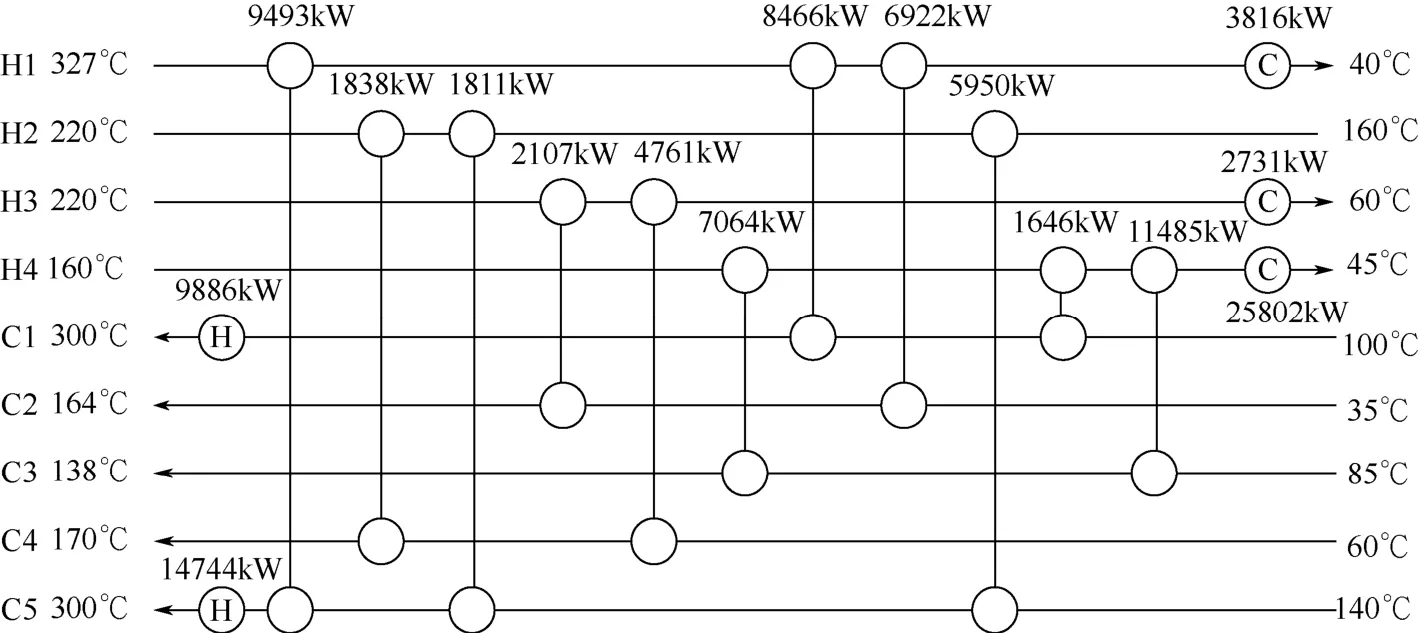
图2　最速下降法求解策略优化结果

由于换热网络综合问题的严重非线性，Lagrange乘子法只能收敛于局部最优解。所以本文分别对图2、图3所示的换热网络结构执行结构进化策略。并在与原Lagrange乘子法参数设置相同的情况下，得到执行结构进化策略前后的费用变化曲线。由于两种求解策略的确定性方法本质，所以收敛较快，在前期每200步记录一个费用值，而结构进化策略具有随机性，得到更优结果所需的计算步骤相对较多，后期每500步记录一个费用值。

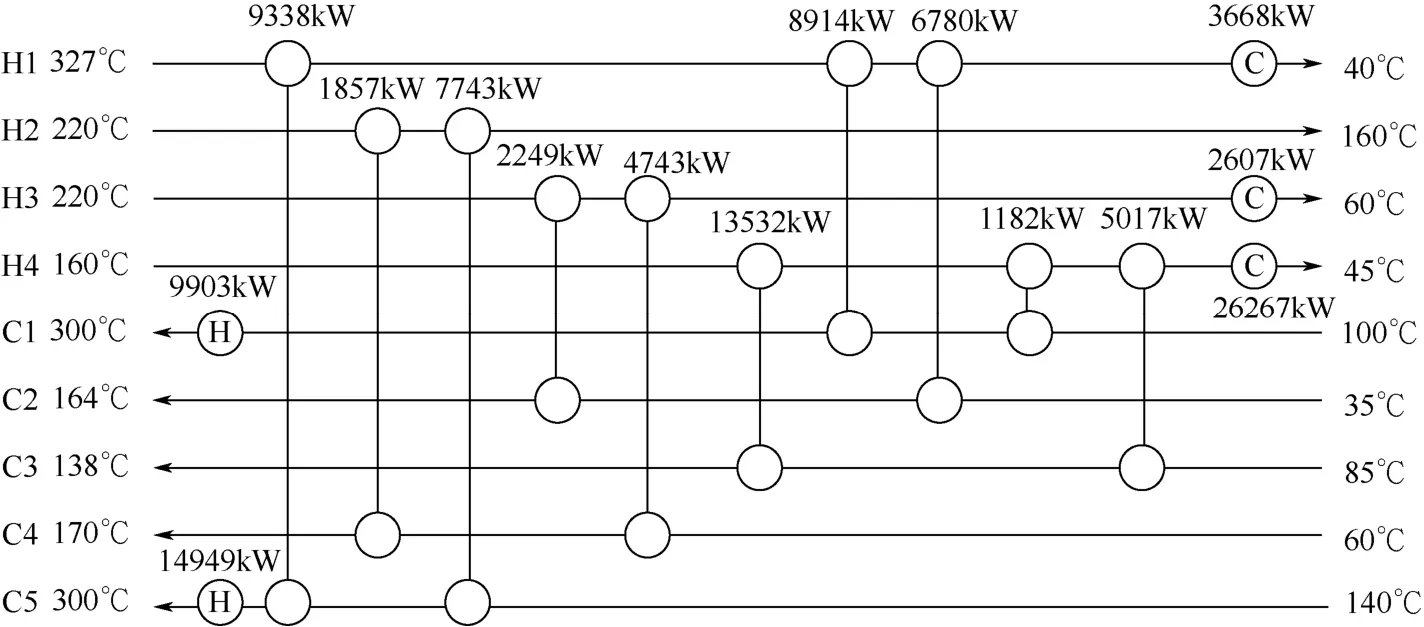
图3　Powell法求解策略优化结果

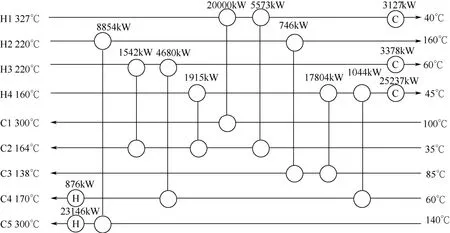
图4　执行结构进化后的最速下降法求解策略优化结果

对图2所示的换热网络结构执行结构进化策略后，得到图4所示结果，其所对应的年综合费用为2927432$/a，相比原结构对应的费用值下降14517$/a。两者的费用变化曲线如图5所示，由其可知，执行结构进化策略后，费用曲线出现了4次明显的下降，而两者对应的换热网络结构也有很大的差异，表明结构进化策略使算法多次跳出了局部最优解，优化后的换热网络结构趋近于最优结构。

对图3所示的换热网络结构执行结构进化策略后，得到图6所示结构，其所对应的年综合费用为2930189$/a，相比原结构对应的费用值下降11964$/a。两者的费用对比曲线如图7所示，由其可知，执行结构进化策略后，费用曲线出现明显的下降，即对当前结构执行结构进化策略后，扩大了Lagrange乘子法的搜索范围，获得了比以往更优的换热网络设计。表明结构进化策略加强了算法的全局搜索能力，提高了搜索效率。

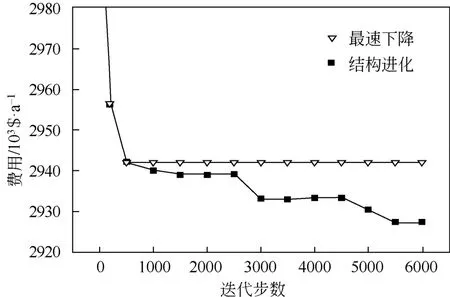
图5　最速下降法求解策略执行结构进化前后的年综合费用对比曲线

优化结果与文献对比如表2所示，由其可知，本文采用的Lagrange乘子法得到了相对于文献更优的结果。对图2、图3所示结构执行结构进化策略后，分别得到图4、图6所示结构，年综合费用均再次出现明显的下降，表明执行结构进化策略后，当前换热网络结构不断向最优结构进化，在原有结果的基础上，提升优化质量。各图所示结构的计算相关参数如表3所示。

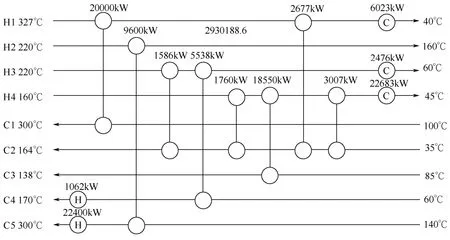
图6　执行结构进化后的Powell法求解策略优化结果

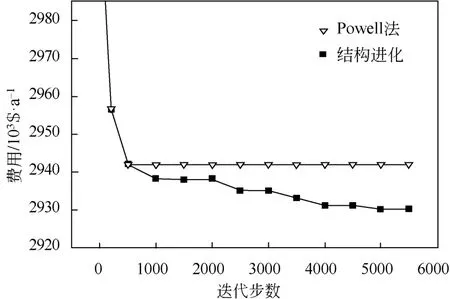
图7　Powell法求解策略执行结构进化前后的年综合费用对比曲线

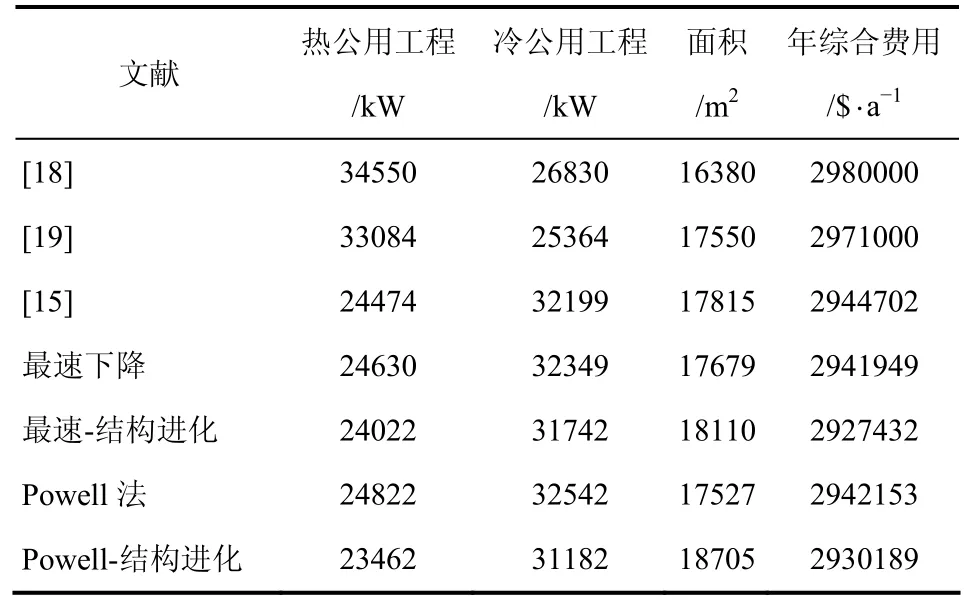
表2　算例结果比较

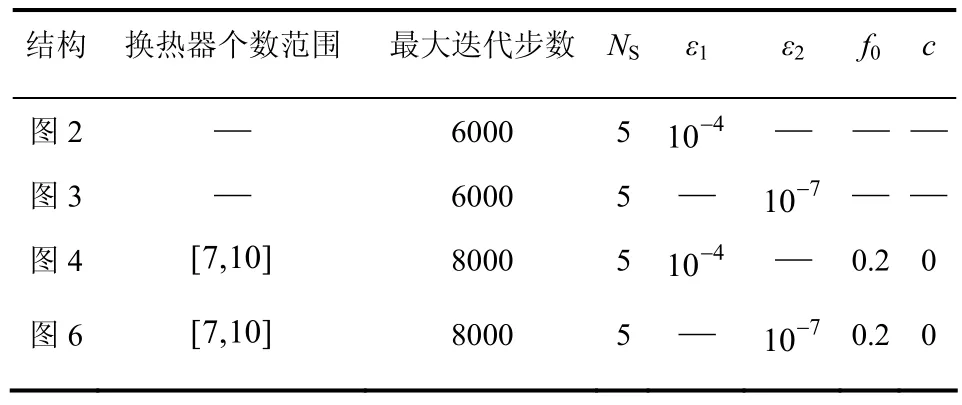
表3　计算相关参数

此外，虽然基于最速下降法求解策略的结果均好于基于Powell法，但Powell法求解策略仍具有了一个所有极小值均为0的新函数，通过优化新函数可以求解方程组。其次，由前述可知，图2、图3的结构可认为近似相同，且费用差值为204$/ a，相对本算例的费用数量级可忽略，即对同一个Lagrange方程组而言，两种求解策略能够得到近似相同的解。图4、图6结构对应的费用值虽然相差2527$/ a，但造成此差异主要是因为两者初始结构的换热器个数不同，对结构进化策略而言，相当于从不同起点进行进化，最终导致结果存在差异。且两费用值均明显优于原结构以及文献结果，进一步表明了结构进化策略在解决换热网络综合问题时的有效性及通用性。

5　结论

本文采用Lagrange乘子法优化换热网络，克服了罚函数法处理有约束问题时存在的不足。结合确定性方法提出的两种求解策略能有效求解Lagrange函数方程组，并使用极小值判断机制对方程组的解进行了检验。根据实际工况提出的结构进化策略与Lagrange乘子法结合，扩大了搜索范围，跳出局部最优解，实现了换热网络的全局最优化。通过经典算例对算法的精度及收敛性等方面进行验证，均取得了不错的结果。

符 号 说 明

参考文献

[1]胡向柏，崔国民，涂惟民. 复杂换热网络MINLP中的非线性特性分析[J]. 工程热物理学报，2012，33（2）：285-287.

[2]FURMAN K C，SAHINIDIS N V. Computational complexity of heat exchanger network synthesis[J]. Computers & Chemical Engineering，2001，25（9）：1371-1390.

[3]YERRAMSETTY K M，MURTY C V S. Synthesis of cost-optimal heat exchanger networks using differential evolution[J]. Computers & Chemical Engineering，2008，32（8）：1861-1876.

[4]LINNHOFF B，HINDMARSH E. The pinch design method for heat exchanger networks[J]. Chemical Engineering Science，1983，38（5）：745-763.

[5]YEE T F，GROSSMANN I E. Simultaneous optimization models for heat integration (Ⅱ)：heat exchanger network synthesis[J]Computers and Chemical Engineering，1990，14（10）：165-1184.

[6]DIPAMA J，TEYSSEDOU A，SORIN M. Synthesis of heat exchanger networks using genetic algorithms[J]. Applied Thermal Engineering，2008，28（14）：1763-1773.

[7]何坚勇. 最优化方法[M].北京：清华大学出版社，2007：387-388.

[8]BERTSEKAS D P. Constrained optimization and Lagrange Multiplier methods[M]. Boston：Computer Science & Applied Mathematics Boston Academic Press，1982：383-392.

[9]AVRIEL M. Nonlinear programming：analysis and methods[M]. Dover：Dover Publications Inc.，2003.

[10]LIN H，WANG Z，LI Z Y，et al. Weighing fusion method for truck scale based on an optimal neural network with derivative constraints and a lagrange multiplier[J]. Measurement，2015，63：322-329.

[11]程雪涛，徐向华，任建勋，等. 用Lagrange乘子法优化并联液体冷却网络系统[J]. 清华大学学报（自然科学版），2008（8）：1359-1361.

[12]郭烨，吴文传，张伯明，等. 拉格朗日乘子法电力系统网络参数错误辨识的应用[J]. 中国电机工程学报，2013（10）：43-49.

[13]于颖，於孝春，李永生. 扩展拉格朗日乘子粒子群算法解决工程优化问题[J]. 机械工程学报，2009（12）：167-172.

[14]GIUFFRÈ S，MAUGERI A，PUGLISI D. Lagrange multipliers in elastic–plastic torsion problem for nonlinear monotone operators[J]. Journal of Differential Equations，2015，259（3）：817-837.

[15]方大俊，崔国民. 微分进化算法应用于换热网络全局最优化[J]. 化工学报，2013，64（9）：3285-3290.

[16]TOLEDO F M B，Armentano V A. A lagrangean-based heuristic for the capacitated lot-sizing problem in parallel machines[J]. European Journal of Operational Research，2006，175：1070-1083.

[17]POWELL M J D. An efficient method for finding the minimum of a function of several variables without calculating derivatives[J]. Computer Journal，1964，7（2）：155-162.

[18]ZHU X X，O’NEILL B K，ROACH J R，et al. A method for automated heat exchanger network synthesis using block decomposition and non-linear optimization[J]. Chemical Engineering Research and Design，1995，73（A8）：919-930.

[19]BRIONES V，KOKOSSIS A C. Hypertargets：a conceptual programming approach for the optimization of industrial heat exchanger networks——I. Grassroots design and network complexity[J]. Chemical Engineering Science，1999，54（4）：519-539.

Lagrange multiplier method combined with structure evolution strategy for heat exchanger network synthesis

ZHANG Chunwei，CUI Guomin，CHEN Shang，TAO Jianan
（Research Institute of New Energy Science and Technology，University of Shanghai for Science and Technology，Shanghai 200093，China）

Abstract：In allusion to the deficiency of penalty functions for constrained problems，a Lagrange multiplier method was adopted to optimize the heat exchanger network. To solve the Lagrange function equations，the steepest-descent method and the Powell method solving strategy according to the deterministic approach were proposed. The minimum value judgment mechanism ensures that the Lagrange function equation solution equals the minimum objective function value of the original network. According to the actual working conditions，a structure evolution strategy combined with a Lagrange multiplier method was proposed to reach the aim of global optimization. The validity and accuracy of these two methods，as well as the universality of the structure evolution strategy were verified by two benchmark problems. Compared with literature results，the proposed approaches have both strong local and global search abilities to find better heat exchanger network structures，which is conducive to cost saving in industrial production.

Key words：heat exchanger network；Lagrange multiplier method；steepest-descent method；Powell method；structure evolution strategy

中图分类号：TK 124

文献标志码：A

文章编号：1000–6613（2016）04–1047–09

DOI：10.16085/j.issn.1000-6613.2016.04.013

收稿日期：2015-09-25；修改稿日期：2015-10-26。

基金项目：国家自然科学基金（51176125）及沪江基金研究基地专项（D14001）项目。