折流式旋转床有效功耗的初步研究

汪建峰，王广全，操伟伟，计建炳（浙江工业大学化学工程学院，浙江 杭州 310014）



折流式旋转床有效功耗的初步研究

汪建峰，王广全，操伟伟，计建炳
（浙江工业大学化学工程学院，浙江 杭州 310014）

摘要：折流式旋转床是一种新型的同心圈式超重力设备，电机功率消耗是折流式旋转床设计时需要考虑的重要因素。本文对折流式旋转床的有效功耗进行了初步的实验研究，并提出了一种新的有效功耗计算方法，为旋转设备功耗研究和折流式旋转床工业应用提供了一定基础。折流式旋转床有效功耗可以分成两部分，即分散液体功耗和加速液体功耗。通过理论分析，得到了折流式旋转床有效功耗的计算模型。实验以水为介质，在不同液量和转速下测得有效功耗。结果表明，转速一定时，有效功耗随着液量的增加近似呈线性增加，且转速越大，有效功耗随液量增加越快。通过对实验数据的回归，得到单个同心圈转子有效功耗的计算模型，实验值与回归计算值相对偏差基本在20％以内。通过对包含4个同心圈转子的折流式旋转床有效功耗的验证结果可知，4个动圈有效功耗计算值的总和比实验测量值高20％左右，对折流式旋转床的工程放大有一定意义。

关键词：折流式旋转床；有效功耗；计算模型

第一作者：汪建峰（1990—），男，硕士研究生。联系人：王广全，博士，副教授，研究方向为传质与分离技术。E-mail wanggq@zjut.edu.cn。

超重力技术是一种有效的过程强化技术，是强化三传一反的有效途径，该技术已在多个领域实现产业化应用[1-3]。超重力旋转床利用离心力场来代替重力场，是实现超重力场下两相流体接触的设备，转子是超重力旋转床的主要部件。目前，已有文献报道的转子结构主要有填料式[4]、螺旋式[5]、多级雾化式[6]、同心环碟片式[7]、撞击流式[8]、折流式[9]等。与传统的两相流体接触设备相比，超重力旋转床增加了电动机。旋转床功耗是旋转设备总功耗中不可忽略的部分，对其的理论与实验研究是旋转床应用与经济分析的双重需要。诸多研究者对旋转床的功耗进行了研究[10-14]。柳松年等[11]认为，旋转床功耗包括有效功耗、气相功耗以及轴承摩擦功耗。有效功耗包括加速液体功耗和分散液体功耗；气相功耗主要为液相在转子内运动时受到气相摩擦阻力的功耗以及转子转动时与空气摩擦的功耗；轴承摩擦功耗主要是转子轴承与旋转床之间的摩擦功耗。贺国等[13]通过实验测定发现，液相受到的气相摩擦阻力几乎为零；柳松年等[11]通过测定发现转子与空气摩擦功耗和轴承摩擦功耗所占总功耗比例均不到1％。因此，旋转床功耗主要为有效功耗，研究旋转床的有效功耗意义重大。寻找既能满足精度要求又易于应用的功耗计算模型对折流式旋转床功耗研究具有重大意义。本文对折流式旋转床的有效功耗进行了理论和实验研究，在理论分析的基础上，结合实验数据，提出了一个半经验半理论的计算模型。

1　理论分析

折流式旋转床主要由折流式转子和壳体组成。转子是折流式旋转床核心部件，为动静组合式结构。动部件为动盘和动圈，静部件为静盘和静圈，动、静部件之间的缝隙提供了气液流动的折流式通道，如图1所示。

操作过程中，气相由气体进口切向进入，在压差作用下，从转子外缘沿着折流式通道向转子中心逐圈流动，经气体出口离开旋转床；液相由进液管进入动盘中心，在离心力的作用下沿着动盘底部向动圈底部聚集，并逐渐向动圈开孔区爬升，经小孔分散成液滴或液丝甩向静圈。液滴在重力作用下从静圈上落到动盘上。液相在转子内重复聚集、爬升、分散、滴落的过程，最后经液体出口排出，如图2所示。

由于液相在每个同心圈上运动规律相同，因此为了研究方便，本文以单个动圈单排液孔的转子为研究对象。实验时，通过测定旋转床液相流量为零时的功耗得到空载功耗；通过测定旋转床液量不为零时的功耗得到旋转床总功耗。旋转床总功耗与空载功耗均由电表测得的电机功耗乘以电机效率ηm和传递效率ηt[14]得到，两者之差即为旋转床有效功耗。根据前文分析，有效功耗分为两个部分，即分散液体功耗和加速液体功耗。这两部分功耗又可通过理论分析得到。

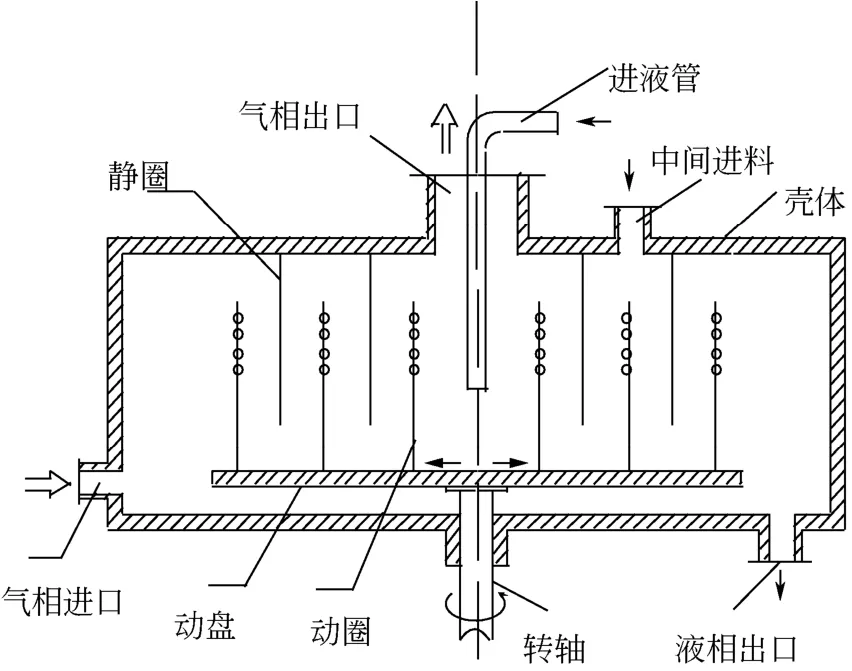
图1　折流式旋转床结构图

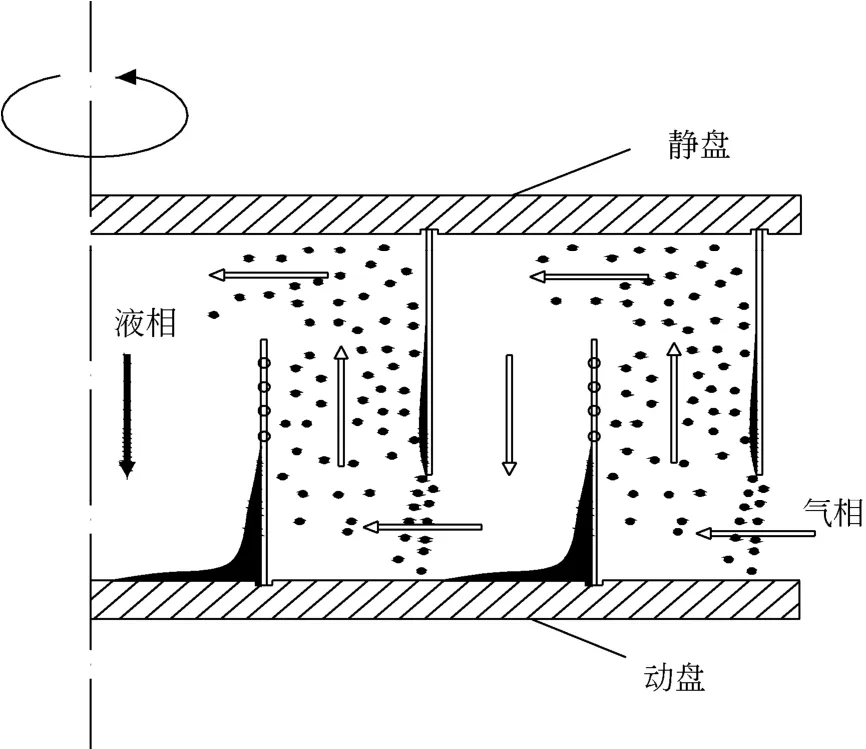
图2　折流式旋转床气液流动图

1.1分散液体功耗

折流式旋转床中，液相在离心力场的作用下由转子中心向转子外沿运动，经动圈上的圆孔被分散成极小的液滴，此过程克服表面张力需要消耗一定功率。单位时间内克服表面张力耗能计算式如式(1)。

式中，As为分散后液滴总表面积。

若液滴作为球形颗粒处理，则分散后液滴总表面积可根据式(2)得到。

式中，液滴直径d可仿照重力场下液体经细圆管滴落时液滴直径计算式得到。在重力场下，液体经细圆管滴落时，液滴直径如式(3)[15]。

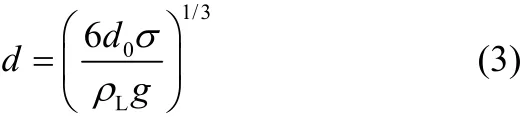
考虑到离心力场远大于重力场，液滴之间相互作用剧烈，运动更加复杂，液滴直径也更难以预测，引入系数B加以修正液滴直径，得到离心力场下液滴直径计算式如式(4)。

这样便可得到单位时间液相克服表面张力耗能的计算如式(5)。

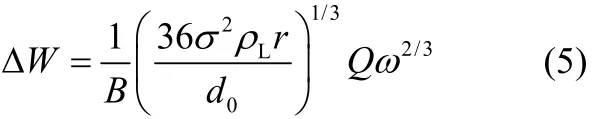
式中，ω为角速度，可由式(6)得到。

将式(6)代入式(5)得到式(7)。

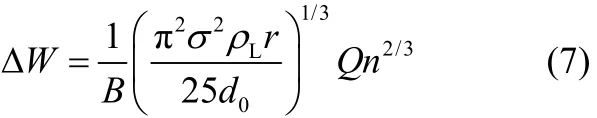
1.2加速液体功耗

液相被引入转子中心后，被高速旋转的动盘和动圈逐渐加速，最终以一定速度离开动圈。假定液滴离开动圈所获得速度为u，进行矢量分解，得到切向速度ut和径向速度ur。由于液相被引入转子后形成液膜的初动能远小于液滴离开动圈时的动能，为了计算方便，忽略液膜初动能。液滴切向速度ut根据动圈圆周速度求得；径向速度ur本应严格按照伯努利方程推导得到的孔流流速计算方法计算，但为了计算方便，采用液量Q与开孔面积A的比值来计算。引入动能修正系数K修正忽略液膜初动能和简化液滴径向速度计算式所引起的偏差，则单位时间内液滴离开动圈获得动能ΔE如式(8)。

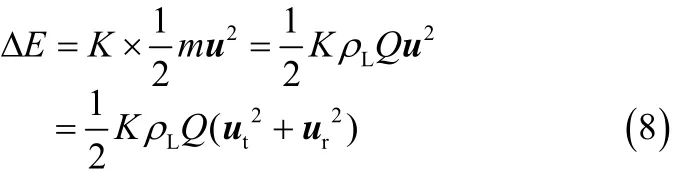
代入液滴切向速度和径向速度计算式可得式(9)。

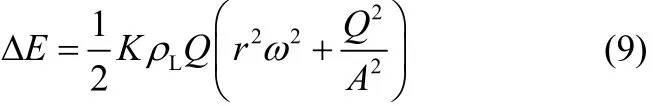
将式(6)代入并整理得式(10)。

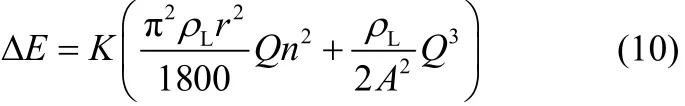
结合分散液体功耗和加速液体功耗计算式便可得到有效功耗计算式如式(11)。

2　实验部分

本文实验采用水为介质，主要由两部分组成，分别为单动圈转子实验和多动圈转子实验。

由于静圈在折流式旋转床中只起到了阻挡液滴的作用，对有效功耗没有影响，所以第一步实验所用的转子也只包含一个动圈，动圈直径235mm，高度70mm。动圈上有一排孔，孔数243，孔径1.6mm，开孔位置距离底盘30mm。实验流程如图3所示，水由进液管引入转子中心，最终由壳体收集经出口排出。

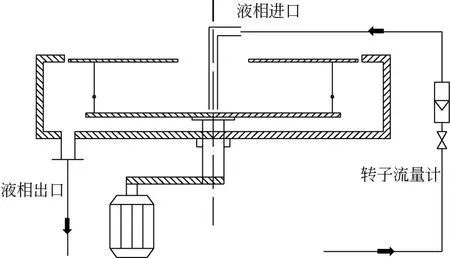
图3　折流式旋转床功耗测定实验流程

实验的主要目的是测得折流式旋转床的有效功耗，因此并未通入气体。实验时，转速通过转速测量仪测量，通过调频器调节，液量通过进液管上的转子流量计测量，旋转床功耗由三相功率表和秒表测量。首先固定转速不变，液相流量为零时，得到旋转床空载功耗；接着改变液量大小，便可得到同一转速不同液量下旋转床总功耗。总功耗与空载功耗之差即折流式旋转床有效功耗。最后改变转速，重复实验，最终得到不同转速、不同液量下折流式旋转床的有效功耗。

根据单动圈转子的折流式旋转床的实验结果，得到有效功耗的关联式并验证之后，再次通过多圈转子实验结果进一步验证。实验转子包含4个动圈，直径分别为165.8mm、102.8mm、234.8mm、265.8mm，动圈上有一排圆孔，孔径1.6mm，孔个数分别为203、240、282、316，实验步骤与单动圈转子实验步骤相同。

3　结果与讨论

对于同一个同心圈，折流式旋转床有效功耗与液量和转速有关。利用式(11)对实验得到的不同转速、不同液量下转子有效功耗的实验数据进行回归，得到有效功耗计算式中动能修正系数K为1.9，液滴直径修正系数B为0.05，从而得到实验所用转子有效功耗关于液量和转速的计算式。理论推导液滴直径计算式时，对液滴作了大小一致的球体处理，而实际液滴运动过程中，由于液滴相互之间的碰撞，液滴形状大小不一。液滴直径修正系数B远小于1，表明液滴之间相互碰撞剧烈，实际液滴直径远小于对液滴做大小一致的球体处理后计算得到的直径；液滴动能修正系数K大于1，表明液滴实际获得的动能大于理论计算得到的动能。这是因为在离心力的作用下，动圈圆孔处与液面表面压差极大，使得液相并未充满所有圆孔，因此根据液量与开孔面积的比值计算得到的径向速度偏小，液相总动能偏小。

将不同转速代入，便可得到不同转速下有效功耗关于液量的计算式。同理，将不同液量代、便可得到不同液量下有效功耗关于转速的计算式。有效功耗计算值与实验值关系如图4和图5所示。

由图可知，折流式旋转床转速一定时，有效功耗随着液量的增加近似呈线性增加。液量增加，一方面，被分散的液体总量增加，则分散液体功耗增加；另一方面，液量增加，加速液体功耗增加。液量一定时，有效功耗随转速增加而增加，且转速越大增加速度越快。回归结果的相对偏差如图6所示。由图6可知，有效功耗的实验测量值与回归计算值的相对偏差基本在20％以内。

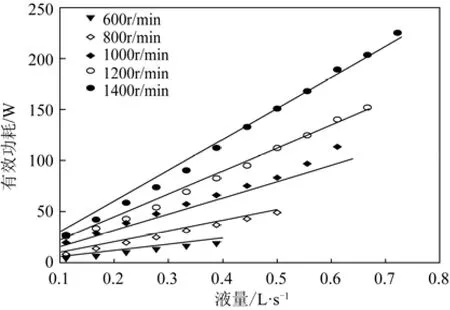
图4　有效功耗与液量关系图

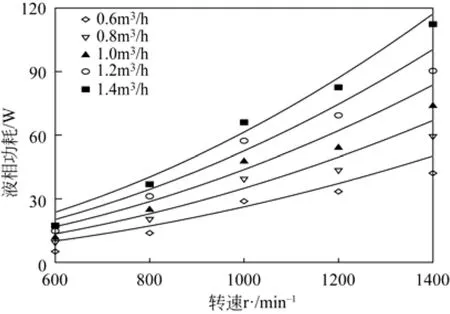
图5　有效功耗与转速关系图

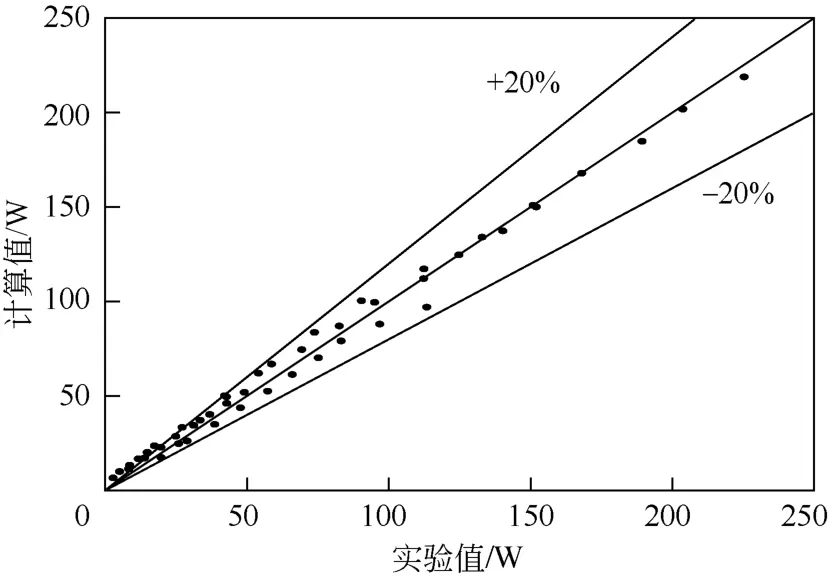
图6　有效功耗回归结果相对偏差图

实验测量值与回归计算值存在偏差，原因主要有3个方面：一方面，推导克服表面张力功耗的计算式时，忽略了液膜表面积初值；另一方面，动圈上的开孔并未全部充满液体，则实际液滴径向速度ur大于Q/A。另外，同一转速下，引入液相之后，转轴摩擦功耗可能发生变化，而本文实验是在假定转轴摩擦功耗不变的基础上进行的。

使用回归计算式分别得到4个动圈的有效功耗，加和后得到有效功耗的计算值与实验测量值进行对比，结果如图7所示。

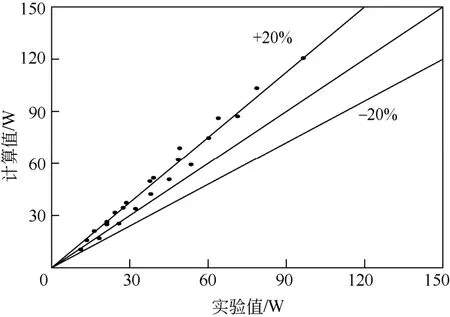
图7　多圈转子有效功耗实验结果相对偏差图

由图7可知，有效功耗计算值比实验测量值高20％左右。这是因为，液相在离心力的作用下从动盘底部向开孔区域爬升，部分液相甚至直接爬升至动圈顶部甩出，而并非经由圆孔分散甩出。这部分液体按照被圆孔完全分散计算得到的分散液体功耗ΔW必然大于实际分散液体功耗，以致总的液相有效功耗的计算值大于实验测量值。

4　结论

本文提出了一种折流式旋转床有效功耗的计算方法，运用此方法得到的单圈有效功耗的计算值与实验值的相对偏差基本在20％以内，为工程研究及应用提供了一定基础。

本文实验研究只是对有效功耗的初步研究，单个动圈有效功耗的规律反映了整个折流式旋转床有效功耗的规律，是折流式旋转床功耗研究的核心部分。理论上说，整个折流式旋转床有效功耗是多个动圈有效功耗的叠加。通过进一步的实验验证可知，多圈转子的有效功耗计算值比实验值高20％左右，对该研究的实际应用有一定的参考价值。

由于实验采用水为介质，实际工业应用中往往是其他液体，其物性与水有很大不同；同时，工业应用中的折流式旋转床气液并存，液相克服气体摩擦也会损耗一定功耗。因此，实际应用中的折流式旋转床有效功耗可根据本文模型进行计算，并结合实际工况进行适当放大，进而选择合适的电动机。

符 号 说 明

参考文献

[1]陈建峰. 超重力技术及应用：新一代反应与分离技术[M]. 北京：化学工业出版社，2002

[2]刘有智. 超重力化工过程与技术[M]. 北京：国防工业出版社，2009

[3]Ramshaw C，Mallinson R H. Mass transfer apparatus and its use：EP 0002568[P]. 1979.

[4]Keyvani M. Operating characteristics of rotating beds[J]. Chemical Engineering Progress，1989，85（5）：48-52.

[5]陈昭琼，熊双喜，伍极光. 螺旋型旋转吸收器[J]. 化工学报，1995，46（3）：388-392.

[6]潘朝群，张亚君，邓先和，等. 多级雾化超重力旋转床中气液传质实验研究[J]. 华南理工大学学报，2006，34（3）：67-71.

[7]简弃非，邓先和，邓颂九. 碟片旋转床气液传质实验研究[J]. 化学工程，1998，26（2）：11-14.

[8]李俊华. 撞击流-旋转填料床合成纳米硫化锌研究[J]. 中北大学学报，2013，34（3）：297-305.

[9]WANG G Q，XU Z C，JI J B. Progress on Higee distillation——introduction to a new device and its industrial applications[J]. Chemical Engineering Research and Design，2011，89：1434-1442.

[10]潘朝群，张燕青，邓先和. 多级雾化超重力旋转床能耗的建模及实验[J]. 华南理工大学学报，2005，33（10）：48-51.

[11]柳松年，郭锴，宋云华. 超重力场分离机的功率分析[J]. 北京化工大学学报，1997，24（1）：51-56.

[12]焦建雄，陈海辉. 旋转填料床的功率实验分析[J]. 株洲工学院学报，2004，18（2）：74-77.

[13]贺国，汪宏伟. AIP系统丝网填料旋转床功耗研究[J]. 华中科技大学学报，2005，33（8）：16-18.

[14]李育敏，折流式旋转床液相功耗数学模型[J]. 高校化学工程学报，2010，24（2）：203-207.

[15]LIU H M. Science and engineering of droplets：fundamentals and applications[M]. New York：William Andrew Publishing，LLC Norwich，2000：121-192.

Preliminary studies on the effective power consumption of rotating zigzag bed

WANG Jianfeng，WANG Guangquan，CAO Weiwei，JI Jianbing
（College of Chemical Engineering，Zhejiang University of Technology，Hangzhou 310014，Zhejiang，China）

Abstract：Rotating zigzag bed（RZB） is a novel kind of HIGEE equipment with concentric rings. Motor power consumption is an important factor to be considered when researchers design RZB. In this paper，experimental studies on the effective power consumption of RZB were preliminarily carried out. A new calculation method was proposed，which provided basis for studies on power consumption of rotating equipments and industrial applications of RZB. The effective power consumption of RZB could be divided into two parts：power consumption to disperse liquid and to accelerate liquid. The calculation model of the effective power consumption of RZB was achieved by theoretical analysis. Using water as test system，the effective power consumption was experimentally measured. According to the experimental data，the effective power consumption approximately linearly increased with liquid flowrate when rotating speed was constant. The higher rotating speed was，the more rapidly effective power consumption increased. Based on the experimental data，the model of effective power consumption with liquid flowrate and rotating speed for rotor with single concentric ring could be achieved. The relative deviation between the experimental data and the calculated values was within 20％. The calculated effective power consumption of RZB with four concentric rings is about 20％ higher than the measured values，which is of certain significance for scale-up of RZB.

Key words：rotating zigzag bed；effective power consumption；calculation model

中图分类号：TQ 018

文献标志码：A

文章编号：1000–6613（2016）04–1022–05

DOI：10.16085/j.issn.1000-6613.2016.04.009

收稿日期：2015-09-23；修改稿日期：2015-11-28。