响应面法对PBGA封装元器件的有限元模型修正

（北京航空航天大学可靠性与系统工程学院，北京100191）

响应面法对PBGA封装元器件的有限元模型修正

张大鹏，李传日

（北京航空航天大学可靠性与系统工程学院，北京100191）

目的利用特殊设计夹具来模仿PCB板的典型插入式固定方式，通过响应面法对安装有PBGA的菊花链PCB板有限元模型进行修正。方法有限元模型经过三次响应面修正，每一个修正阶段都计算仿真前三阶频率与相对应的模态试验结果相对比，建立两个目标函数，并利用多目标遗传算法来缩小仿真分析与模态试验结果。结果有限元模型得到了有效的改善。结论响应面法可以从实际出发来提升有限元模型准确度。

PBGA；模态试验；有限元模型；响应面；模型修正

有限元模型的准确性是分析模型特性的关键所在。尽管许多文献表明材料属性和PCB边界条件对PCB板仿真影响较大[1—2]，但很少学者提及到PCB校正的过程。在PCB模型校正过程需要用到试验结果来对原始不确定的模型参数进行修正并得到更接近真实情况的模型。早期有限元模型的校正包括直接法[3—4]和迭代法[5—6]。运用直接法修正单元的质量刚度矩阵可以与试验结果很好吻合，然而，修正后的矩阵通常会失去结构本身特性，从物理意义角度来看，这种修正结果有时候也会变得不合理。采用迭代法计算参数敏感度并利用泰勒展开式寻找输入参数变化量，当模型变得复杂后，这种方法就会变得特别耗时也不方便实现。响应面法更适合于快速修正模型并得到很好的修正结果[7—9]，这种方法通过试验设计方法得到一定修正参数的样本点，并计算这些样本点的值，通过样本点创建新的模型并计算其响应输出值，通过将仿真输出值接近试验结果创建目标函数，并通过迭代计算得到修正后的参数。

文中讲述了一种根据响应面法对有限元模型进行修正使得模型更加接近真实情况的方法。自行设计的菊花链PCB板上安装有PBGA元器件，通过特殊设计夹具来模拟PCB板的典型插入式固定方式，并对PCB板进行固定。通过Ansys进行有限元模型，并通过三个阶段进行模型修正。首先对PCB板、PCB组件自由状态及PCB组件固支情况下进行模态试验，得出模态频率及模态振型。然后分别对PCB板的材料参数、PBGA基板材料参数及PCB边界条件进行有限元建模及模型修正。使有限元模型与模态试验数据相吻合，得到较为符合实际情况的有限元模型。

1 模态试验

模态试验采用“单输出、单输出”方式进行，利用一个加速度计固定在一个自由度上，通过力锤敲击结构产生输入信号。力锤和加速度连接到多通道快速傅里叶变换分析仪上采集信号并计算其频响函数。将加速度计依次安装在所有测试点上收集信号，并创建输入输出传递矩阵，然后通过时域最小二乘法和频域曲线拟合技术提取模态参数。

首先，对PCB板进行自由模态试验。菊花链PCB板材料为FR4，外形尺寸为203 mm×140 mm×1.6 mm。将PCB板划分35个试验测试点，模态试验和测量点如图1所示。

将两个PBGA元器件焊接在PCB板上，PBGA基板外形尺寸为35 mm×35 mm×1.9 mm。对安装有PBGA元器件的PCB板进行模态试验，测试点如同PCB板的模态试验，如图2所示。

图1 PCB板模态试验测试点分布情况Fig.1 Modal test setup and measurement points of PCB

图2 PCB组件模态试验Fig.2 Modal test setup of PCBA

文中所研究边界条件为典型PCB板插入式固定边界条件，广泛应用在机载电子箱中。PCB板通过一个插入式连接器和两个楔形锁固定在机载电子箱内，如图3所示。

图3 典型插入式PCB板和机载电子箱Fig.3 Typical plug-in PCB and AEC

对PCB组件在特殊设计夹具固支下进行模态试验如图4所示，其测试点和PCB板的模态试验相同。

2 基于响应面法的模型修正

响应面模型是用来表示有限元模型的函数模型，利用响应面函数模型代替所构建的有限元模型进行迭代优化求得参数最优解，以实现模型修正的目的[10]。

利用响应面方法对结构进行模型修正的具体过程归纳如下：

图4 PCBA三边固支情况下模态试验Fig.4 Modal test setup of PCBA and fixture

1）选取修正参数（如果修正参数过多就要用到相关性分析）；

2）利用试验设计对修正参数进行抽样，并计算样本点组成的有限元模型输出值；

3）利用线性回归建立修正参数与响应输出值的响应面，并进行回归误差分析；

4）通过结构仿真和试验测量得到响应特性建立目标函数，并进行迭代优化计算得到响应面模型。

所选取修正参数与输出响应值之间敏感度要高。如果修正参数过多，可以通过相关性分析来减少修正参数的数量。

对修正参数进行样本点采样方式将会影响响应面模型的准确性以及计算效率。对修正参数进行采样和建立响应面时利用广泛应用的正交试验设计方法得到样本点。正交试验设计方法利用正交表设计试验，选取修正参数样本点[11]。

常用的表示响应面形式的是多项式形式。由于其计算简单，并且多项式函数为一闭式表达式[12]。文中利用二次多项式进行响应面拟合：

式中：β0，βi，βij为回归系数；y为响应面输出值；x为修正参数；k为修正参数的个数。

利用样本点数据和最小二乘法拟合响应面。所得到的响应面在使用前要检验其拟合的准确度。利用R2准则进行检验：

式中：N为样本点数量；yi为第i个样本点输出响应真实值；y·i为第i个样本点回归分析的响应值；y为yi的平均值。R2的值在0到1之间，R2越接近1，表明响应面模型越准确[13]。

安装有PBGA元器件的PCB组件有限元模型修正分为三个阶段，这三个阶段分别修正PCB板材料参数、PBGA基板材料参数和PCB板边界条件。在每个阶段中，利用Ansys计算仿真PCB板前三阶频率并利用模态试验结果进行模型修正。建立两个目标函数求解修正参数。第一个目标函数为仿真和模态试验一阶频率差值；第二个目标函数为仿真和模态试验前三阶共振频率残差平方和。两个目标函数具有相同权重。

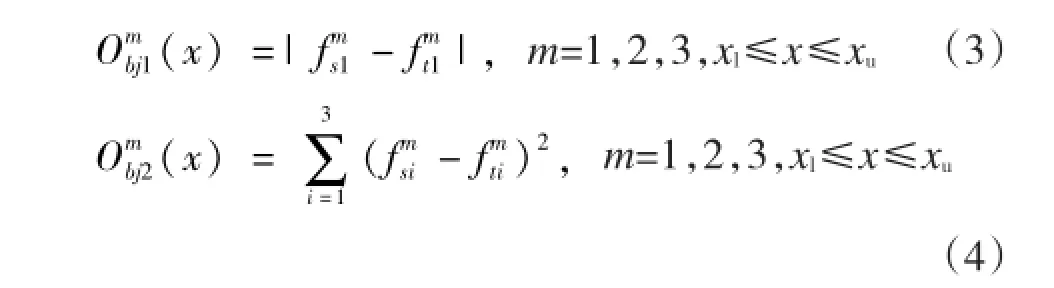
式中：m为修正阶段编号；fsi为仿真共振频率；ft1为模态试验共振频率值；i为模态阶数；x为修正参数；xu和xl分别为修正参数上下限。利用多目标遗传算法对目标函数值进行优化最小值计算。

2.1 修正PCB材料参数

利用Ansys建立PCB板有限元模型，包括200个壳单元，每个单元包括4个节点，每个节点有6个自由度。通过自由模态分析有限元模型，求得前三阶模态。

利用MAC矩阵对模态仿真和试验结果进行检验。MAC矩阵用来评价向量之间相关程度：

式中：ui为第i阶模态仿真振型矩阵；ej为试验第j阶模态试验振型矩阵。

MAC值在0到1之间，其值越接近1表面两向量相关性越好。仿真和试验前三阶模态阵型的MAC值见表1，根据表1可知两者具有很好的相关性。

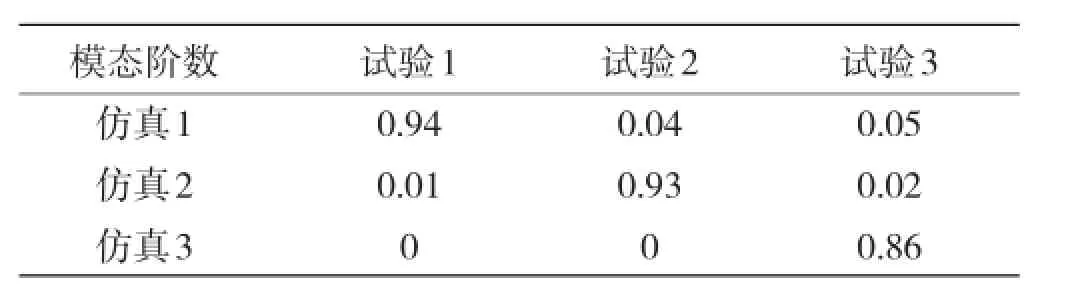
表1 第一阶段模态仿真和试验MAC值Table 1 MAC value of FEA and test modes in stage 1

第一修正阶段内，PCB材料为各向异性，包括3个杨氏模量，3个泊松比和3个剪切模量。将这9个材料参数进行相关性分析[14]，结果见表2。从表2可知，目标函数只与Ey和Gxy两个参数相关性较高。相关性为正，表明响应值随修正参数增大而增大；若为负，则随修正参数增大而减小[15]。

表2 修正参数与目标函数之间相关性Table 2 Correlation between updating parameters and object functions

将Ey和Gxy两个参数作为最终修正参数。利用试验设计方法对参数在其取值范围内进行采样，得到10个样本点。两个目标函数响应面如图5所示。前三阶频率R2值都接近1，表明拟合度较好。PCB板材料修正前后的Ey值分别为16.7，19.2 GPa，Gxy值分别为3.28，3.58 GPa。修正前后前三阶频率对比见表3。从表3可知，前三阶频率误差都减小。

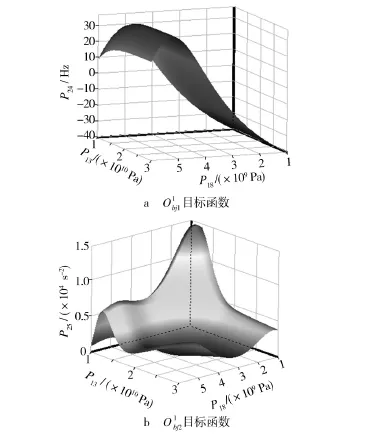
图5 第一阶段两个目标函数的响应面Fig.5 Response surface of two objective functions in stage 1

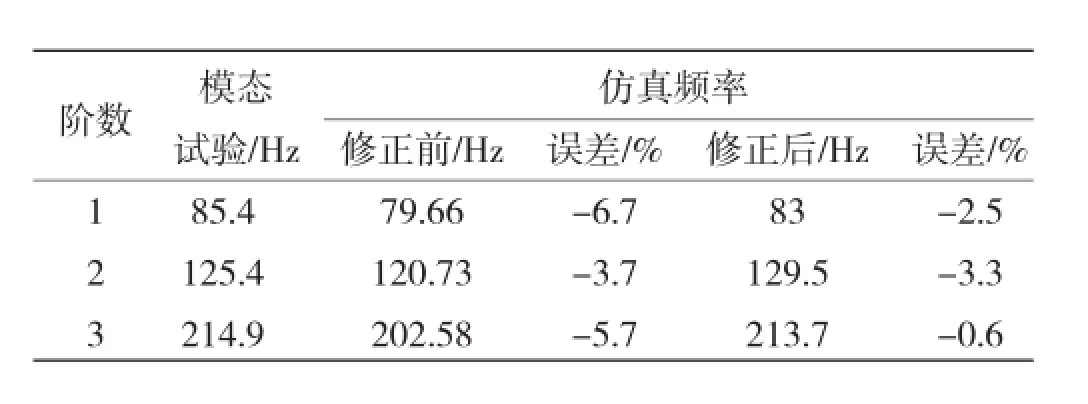
表3 第一阶段修正前后前三阶频率对比Table 3 Comparison of the first three resonant frequencies before and after updating stage 1

2.2 修正PBGA基板材料

利用Ansys建立有限元模型，如图6所示。PBGA元器件和焊点由实体单元组成，每个单元包括20个节点，每个节点具有3个自由度。PBGA元器件四个边角处焊点进行详细建模，其他焊点利用长方体进行近似代替。通过自由模态分析有限元模型前三阶模态。

图6 安装PBGA的PCB有限元模型Fig.6 FE model of PCB installed with PBGA

有限元仿真和试验模态振型MAC值对比见表4。从表4可知，两者具有很好相关性。

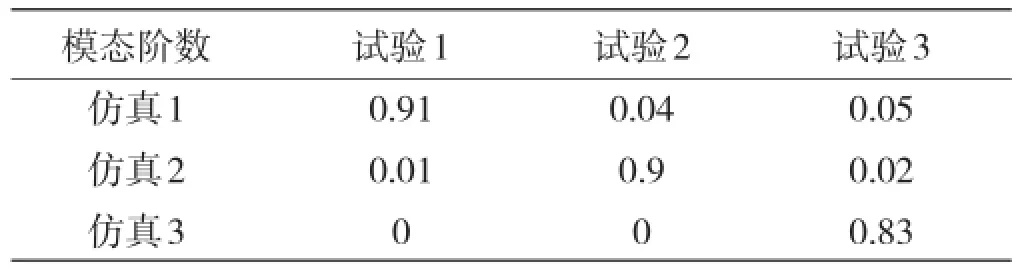
表4 第二阶段模态仿真和试验MAC值Table 4 MAC value of FEA and test modes in stage 2

假定PBGA基板材料为各向同性，将杨氏模量和泊松比作为修正参数。由于修正参数只有两个，所以没有必要进行相关性分析，其响应面如图7所示。前三阶共振频率R2检验值均接近1。PBGA基板材料参数E修正前后的值分别为20，13 GPa，μ修正前后的值分别为0.3，0.23。频率比较见表5，从表5可知，前三阶共振频率误差都减小。

图7 第二阶段两个目标函数的响应面Fig.7 Response surface of two objective functions in stage 2

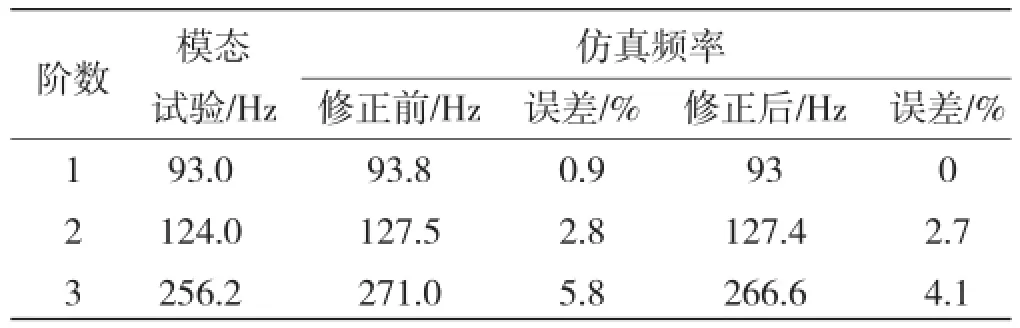
表5 第二阶段修正前后前三阶频率对比Table 5 Comparison of the first three resonant frequencies before and after updating stage 2

2.3 修正边界条件参数

在第三修正阶段，对模拟的插入式边界条件参数进行修正。由于“固支”方式的边界条件在现实中是不存在的，利用“固支”方式来模拟插入式连接器和楔形锁就会导致很大的误差。为了更好模拟PCB板插入式固定的边界条件，通过Ansys进行夹具建模如图8所示。

通过旋转弹簧限制节点的旋转自由度的方式来模拟插入式连接器和楔形锁的固定方式。PCB板边界与相对应夹具的节点平动自由度进行耦合。将模拟楔形锁的夹具弹簧刚度视为K1；将模拟插入式连接器的夹具弹簧刚度视为K2。

图8 PCB组件及夹具有限元模型Fig.8 FE model of PCBA and fixture

模态仿真和试验阵型MAC检验值见表6。根据表6可知，两者具有很高相关度。两个目标函数响应面如图9所示。前三阶共振频率R2值都接近1。

表6 第三阶段模态仿真和试验MAC值Table 6 MAC value of FEA and test modes in stage 3

图9 第三阶段两个目标函数的响应面Fig.9 Response surface of two objective functions in stage 3

旋转弹簧系数K1修正前后的值分别为1.0×104，2.3×104N·mm/rad，K2分别为1.0×106，9.0×106N·mm/ rad。修正模型前后的前三阶共振频率对比见表7。

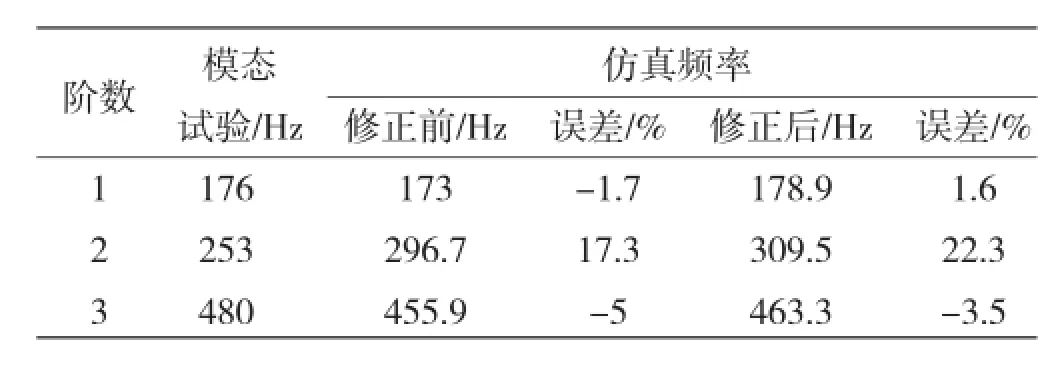
表7 第三阶段修正前后前三阶频率对比Table 7 Comparison of the first three resonant frequencies before and after updating stage 3

从表7可知，尽管模态仿真第二阶共振频率误差值仍然很大，但第一阶和第三阶共振频率与模态试验误差得到改善。第二阶共振频率相对误差较大的原因可能是由于夹具设计时存在缺陷，比如夹具材料刚度不足，导致夹具夹紧过程中发生弯曲，结果导致边界条件变得复杂。除了这一阶模态，由表3、表5和表7可知，响应面法模型修正能够很好地使仿真模态频率更加接近真实模态试验结果。

3 结语

通过有限元建模及模型修正可以很好地模仿真实情况，并提取实际情况很难得到信息。基于响应面有限元模型修正可以快速准确地对有限元模型进行修正，并得到很好的结果。

[1]AMY R A，AGLIETTI G S，RICHARDSON G.Sensitivity Analysis of Simplified Printed Circuit Board Finite Element Models[J].Microelectronics Reliability，2009，49（7）：791—799.

[2]AMY R A，AGLIETTI G S，RICHARDSON G.Accuracy of Simplified Printed Circuit Board Finite Element Models[J]. Microelectronics Reliability，2010，50（1）：86—97.

[3]BERMAN A.Optimal Weighted Orthogonalization of Measured Modes-Comment[J].AIAA Journal，1979，17（8）：927—928.

[4]BARUCH M.Optimization Procedure to Correct Stiffness and Flexibility Matrices Using Vibration Tests[J].AIAA Journal，1978，16（11）：1208—1210.

[5]FRISWELL M I，MOTTERSHEAD J E.Finite Element Model Updating in Structural Dynamics[J].Dordrecht，Kluwer Academic Publishers，1995，38：158—226.

[6]MOTTERSHEAD J E，FRISWELL M I.Model Updating in Structural Dynamics：a Survey[J].Journal of Sound and Vibration，1993，167（2）：347—75.

[7]GUO Q T，ZHANG L M.Finite Element Model Updating Based on Response Surface Methodology[C]//Proceedings of the 22nd International Modal Analysis Conference.Dearborn，Michigan：SEM，2004.

[8]REN W X，CHEN H B.Finite Element Model Updating in Structural Dynamics by Using the Response Surface Method [J].Engineering Structures，2010，32（8）：2455—2465.

[9]ZHOU L R，YAN G R，OU J P.Response Surface Method Based on Radial Basis Functions for Modeling Large-scale Structures in Model Updating[J].Computer-Aided Civil and Infrastructure Engineering，2013，28（3）：210—226.

[10]KWON Joong-hak，HWANG Sang-moon，LEE Chang-min，et a1.Application of Response Surface Methodology in Microspeaker Design Used in Mobile Phones[J].Institute of Electrical and Electronics Engineers Transactions on Magnetics，2009，45（10）：4550—4553.

[11]RUTHERFORD BM，SWILER LP，PAEZ TL，et al.Response Surface（Meat-model）Methods and Applications[C]//Proceedings of the 24th International Modal Analysis Conference. Louis，MO，SEM，2006：184—197.

[12]罗小玲，朱立新.适应细分二次多项式响应面算法[J].微计算机信息，2012（2）：172—174. LUO Xiao-ling，ZHU Li-xin.Adaptive Regressive Quadratic Polynomial Response Surfaces with Domain Decomposition [J].Microcomputer Information，2012（2）：172—174.

[13]秦玉灵.基于响应面建模和改进粒子群算法的有限元模型修正方法[D].哈尔滨：哈尔滨工业大学，2011. QIN Yu-ling.Finite Element Model Updating Method Based on Response Surface Modeling and the Improved PSO Algorithm[D].Harbin：Harbin Institute of Technology，2011.

[14]万黎，毛炳启.Spearman秩相关系数的批量计算[J].环境保护科学，2008（5）：53—55. WAN Li，MAO Bing-qi.Batch Calculation of Spearman Rank Correlation Coefficient[J].Environmental Protection Science，2008（5）：53—55.

[15]张治成.桥梁施工控制中的结构设计参数敏感性分析[J].武汉理工大学学报，2006（10）：77—81. ZHANG Zhi-cheng.Sensitivity Analysis of Structural Design Parameters for Construction Control of Bridge[J].Journal of Wuhan University of Technology，2006（10）：77—81.

Finite Element Modeling for PBGA Components Based on RSM modification

ZHANG Da-peng，LI Chuan-ri
（Reliability and System Engineering Institute，Beihang University，Beijing 100191，China）

Objective A specially designed fixture was used to mimic the typical boundary condition of plug-in PCB.A procedure based on response surface method(RSM)was proposed for modifying the finite element(FE)model of plastic ball grid array(PBGA)components mounted on daisy chain PCB.Methods The FE models were updated by RSM in three stages.In each stage,the first three resonant frequencies were calculated and contrasted with corresponding modal test results.Two objective functions were created and the difference between the simulation analysis and modal test results was minimized using a multi-objective genetic algorithm(MOGA).Results The FE model was effectively improved.Conclusion RSM could be used to improve the accuracy of the FE model in a practical way.

PBGA;modal test；FE modeling；RSM；model modification

LI Chuan-ri（1964—），Male，Professor,Researcher，Research focus：product environmental engineering and reliability test technology．

10.7643/issn.1672-9242.2016.02.010

TJ01；TP211+.5

：A

1672－9242（2016）02－0052-06

2015-10-07；

2015-11-08

Received：2015-10-07；Revised：2015-11-08

张大鹏（1987—），男，黑龙江鸡西人，硕士研究生，主要研究方向为产品环境与可靠性试验。

Biography：ZHANG Da-peng（1987—），Male，from Jixi，Heilongjiang，Master graduate student，Research focus：environmental and reliability test of products．

李传日（1964—），男，教授，研究员，主要研究方向为产品环境工程、可靠性试验技术。