融资融券背景下证券配对交易策略研究——基于协整和距离的两阶段方法

胡伦超，余乐安，汤 铃

(1.中国科学院数学与系统科学研究院，北京 100080；2.北京化工大学经济管理学院，北京 100029)



融资融券背景下证券配对交易策略研究
——基于协整和距离的两阶段方法

胡伦超1，余乐安2，汤 铃2

(1.中国科学院数学与系统科学研究院，北京 100080；2.北京化工大学经济管理学院，北京 100029)

国内融资融券政策的正式启动，为证券配对交易实施提供了必要的市场环境，使其成为一种新兴有效的投资手段。基于协整配对法和距离配对法，本文构建了一种新的两阶段配对交易策略。在股票配对选择方面，首先采用协整分析选出具有相似股价走势的候选股票对；其次，采用欧式距离计算各候选配对股票距离，以距离最小为依据选择最佳股票配对，以避免同一股票同时被买入和卖空的风险。在资金分配方面，考虑当前融资融券交易制度背景，求解资金有限约束下的最优资金分配方案，以保证模型设计更为接近实际交易情况。以上证50指数成分股为实证对象，实证研究结果表明不同费率情景下，构建的新两阶段方法均能获得超额收益，且其效果明显优于仅考虑协整关系的配对交易策略；同时，敏感性分析验证了新方法的稳定性。

投资组合；配对交易；协整分析；距离估计；融资融券

1 引言

2010年3月31日，沪深交易所融资融券试点正式启动，这对中国金融市场的发展具有里程碑的意义。融资融券政策的实施，为投资者进行对冲交易提供了市场环境，投资者迎来了做空获利的时代。与传统的低买高卖投资策略不同，做空股票也可以获利。虽然近年来中国股市长期处于震荡市场行情中，两融业务却保持了可观的增量。截止到2014年12月31日，沪深股票市场融资融券余额为93,803,573.13万元，比2013年同比增长191.29%。

两融业务快速发展的一个主要因素涉及配对交易策略的广泛实施。配对交易策略最先起源于美国的华尔街，是一种经典的量化投资策略，遵循买强卖弱的原则，其主要的思想是寻找两只股价走势相似的股票，并跟踪二者的价格走势，当两者走势出现明显偏离时，买入弱势股票并卖出强势股票，当价差回复到正常水平时则进行平仓操作[8]。配对交易策略是一种市场中性交易策略，受到机构投资者和对冲基金的一致认可[17]，迄今为止仍然是一种优秀的投资策略[12]。

股票配对的选择是配对交易策略制定中的重要步骤，主要涉及三种方法，分别是由Gatev等[8]提出的基于距离的股票配对方法(Distance Method)，由Vidyamurthy[14]提出的基于协整的方法(Cointegration Method)和由Elliott等[5]提出的基于随机价差的方法(Stotastic Spread Method)。各方法具有不同的优势和劣势。其中，基于距离的股票配对方法简单直接，在实证中得到广泛的应用。例如，Gatev等[8]通过对S&P500指数成分股的配对交易研究，指出基于距离法的配对策略能获得超额收益。Nath[13]针对风险引入了止损条件，并证明改进后的距离配对策略相比基准模型能提供更高的收益。麦永冠和王苏生[17]将距离配对法应用于沪深A股市场的投资组合研究中。然而，距离配对法存在着对价差收敛时间和期望持有时间预测能力不足的缺陷[15]。

协整技术能有效估计两两股票的历史价格走势及其价差偏离程度，被广泛应用于配对策略构造中[1, 8-9]。例如，Lin Yanxia等[11]将协整配对法应用于澳大利亚交易所的投资决策研究中，结果表明该方法能获得持续收益；Hong和Raul[10]应用该方法对美国市场64只股票进行配对交易，同样获得显著收益；Vidyamurthy[14]从理论上对协整配对法进行了具体阐述。金恺[19]采用协整配对方法对沪深300指数成分股进行了配对交易研究。然而，基于协整的配对法仍具有不可避免的缺陷，如模型指定偏误、参数估计偏误，以及格兰杰检验变量选择等问题。

基于随机误差法的股票配对法认为股票价差由某一隐变量驱动，且其隐变量遵循Vasicek过程。然而，该模型限制配对股票的长期收益必须一致，且模型复杂性较高，相关实证研究较少[4]。

鉴于各单方法均有优劣，有机结合多种方法的混合配对法能有效克服各单方法的不足，并充分发挥其优势。因此，一些混合多阶段配对交易策略被相应提出。例如，Miao[12]结合相关性分析与协整分析提出了一个新的两阶段配对策略，并以美国股票市场为研究对象验证了该策略能产生高于S&P500指数的收益。徐沐霖[23]将该方法推广到沪深300指数成分股的配对交易中，其结果表明该模型能够在中国股票市场的投资中带来超额收益。

综上，本文拟有机组合距离配对法与协整配对法，构建一种新的两阶段配对交易策略。具体的，在股票配对选择上，首先采用协整分析选出股价走势具有协整关系的候选股票对；在此基础上，采用距离法计算各候选配对股票间的欧式距离，以距离最小为依据构建最佳配对组合，从而避免了同一股票同时被买入和卖空的风险。在资金分配方面，本文着重考虑国内融资融券交易制度框架，求解资金有限约束下的最优资金分配方案。实证研究以上证50指数成分股为研究对象，以验证模型的有效性与稳定性。

2 模型描述

2.1 研究框架

配对交易策略中现有的股票配对方法主要包括距离法、协整法和随机误差法等三种方法[14]。鉴于各方法具有不同的优势和不足，本文基于协整配对法和距离配对法，拟构建一个新的两阶段配对交易策略，即基于协整与距离的两阶段配对交易策略。在股票配对选择上，首先采用协整方法选出股价走势相似的候选股票对，然后计算各候选配对股票的欧式距离，以距离最小为依据构建最佳配对交易组合，以避免同一股票同时被买入和卖空的风险。在资金分配方面，本文采用了Lin Yanxia等[11]提出系数中性策略，并考虑国内融资融券的交易制度的框架，求解出资金有限情况下的最优资金分配方案。相应地，本文的研究框架如图1所示。

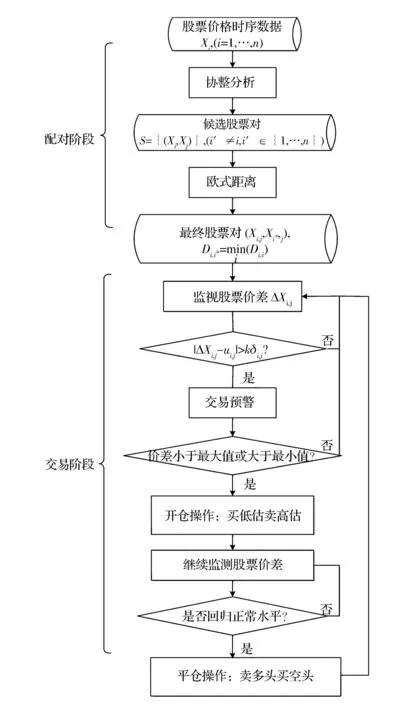
图1 基于协整与距离的两阶段配对交易策略流程图

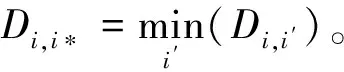
在交易阶段，监测每对股票对价差ΔXi,j，当价差偏离正常水平超过给定阈值kδi,j时，发出交易预警并在价差上升到最大值或者下降到最小值，开仓进行交易，买入相对低估的股票，同时卖出相对高估的股票。当发现价差回复到均值时或者交易期结束，则进行相反的平仓交易，即卖出多头寸买入空头寸。特别的，在资金分配方面，需满足融资融券制度下的保证金、折现率和维持保证金等政策要求，并采用系数中性进行组合计算。

2.2 方法技术

下面将介绍两阶段配对交易策略中所采用的相关技术方法。其中，股票配对阶段结合基于协整的股票配对法与基于距离的股票配对法。交易阶段采用协整系数加权策略(CCW)，并考虑交易费与融资融券背景对该策略进行改进，以确保模型设计更为接近实际交易情况。

2.2.1 基于协整的股票配对法

Alexander等[2]证明两只股票之间的潜在套利需满足两个条件：一是两者存在长期的均衡利差；二是短期利差偏离长期均衡。相应的，一个有效的配对交易方法必须要满足两个条件：一是要能够有效地模拟股票价格走势，并探测股票价格间的相关关系；二是能够度量短期价差偏离长期均衡价差的程度[11]。协整分析因具有这两方面优势从而被广泛应用于配对交易研究中[ 1,9]。

Granger于1981年提出了协整(Cointegration)的相关概念与假设，并与Engle于1987年给出严谨的数学证明和可操作步骤。协整模型假设，受经济系统内在机制作用，各经济变量间往往存在着长期的均衡关系，即使某些变量短期内偏离了长期均衡，该内在机制也会促使变量逐渐调整使其回到均衡状态。

如果一个时间序列是平稳的，我们称之为I(0)过程；如果一个时间序列不平稳，但是经过d(d>0)次差分后变成平稳，我们称之为I(d)过程。协整的定义为，对于多个序列X1,t、X2,t…Xn,t，它们都是I(1)过程，即经过一阶差分后为平稳序列，如果存在非零系数β1,β2,…,βn使序列β1X1,t+β2X2,t+…+βnXn,t服从I(0)过程，则称X1,t、X2,t…Xn,t具有协整关系。

在配对交易研究中，Vidyamurthy[14]引入协整方法分析股票对是否具有协整关系[7]。已知股票对Xi,t和Xj,t，其协整分析方程为：

Xi,t-βi,jXj,t=ui,j+εt

(1)

其中，βi,j为协整系数，常数量ui,j表示两股票的平均溢价。对回归残差序列εt进行Dickey-Fuller(ADF)检验，判断是否为平稳序列。如果残差序列是平稳序列，则表示该股票对具有长期的协整关系，且残差具有均值回归的特性。

在配对交易策略中，模型首先采用协整分析两两股票关系，将具有协整关系的配对组合放入配对候选池S中，即候选股票对(Xi,t,Xi′,t),(i′≠i,i′∈{1,…,n})。然而，在配对候选池S中，某些股票可能与多只股票同时存在协整关系，直接构建股票对组合进行交易，该股票存在同时被买入和卖空的风险。为此，本模型引入距离法确定最终股票配对。

2.2.2 基于距离的股票配对法

距离方法是一种非参数方法，在配对交易中得到广泛的应用。基于距离的股票配对方法由Gatev等[8]提出。首先，计算各股票对(Xi,t,Xi′,t)的欧式距离：

(2)

其中Pi,t为股票i在t期规范化后的价格，T为配对形成期数，i′∈{1,…,n}为配对候选池S中与股票i配对的某一股票。Di,i′越小，表明股票对(Xi,t,Xi′,t)的价格走势越一致，越适合组成股票配对。

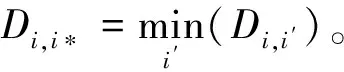
2.2.3 协整系数加权策略(CCW)

在交易阶段中，本文采用LinYanxia等[11]的协整系数加权(CointegrationCoefficientWeighting,CCW)策略进行对冲交易，这种方法属于系数中性分析方法，而非货币中性分析方法。

具体的，对股票对(Xi,t,Xj,t)，假设股票i为被高估的股票，股票j为被低估。当满足开仓条件时，卖空相对被高估的股票i，买入被低估的股票j；当达到平仓条件时，则反向操作，即卖出股票i买入股票j。在不考虑交易费用的情况下，利润核算如下：

NPi,j=Si,to·(Xi,to-Xi,tc)+Sj,to·(Xj,tc-Xj,to)

(3)

其中，Xi,to为股票i在to时刻的价格，Si,to为相应的交易股数，to与tc为进行开仓与平仓操作时刻。显然，NPi,j>0表示该配对交易获利，而NPi,j<0则表示该配对交易亏损。在股票i和j满足协整关系的条件下，且协整系数大于零(βi,j>0)，依据CCW交易策略原则，卖出股票i与买入股票j的股数比为1：βi,j。将(1)式代入(3)式可得到利润：

NPi,j=s·(Xi,to-Xi,tc)+s·βi,j·(Xj,to-Xj,tc)=s·{[Xi,to-βi,j·Xj,to]-[Xi,tc-βi,j·Xj,tc]}=s·{(u+εto)-(u+εtc)}=s·(εto-εtc)

(4)

其中，s为卖出股票i的股数。根据公式(4)，协整系数加权策略(CCW)的收益可由s、εto和εtc所决定。为了保证收益为正，应满足开仓时两股价差偏离长期均值程度εto大于平仓时的价差偏离均值程度εtc。对此，Gatev等[1]和Bogomolov[18]等设定εto需大于配对形成期内价差标准差δi,j的k倍。

如果价差偏离的程度达到触发开仓条件，且价差最终收敛到均值水平，则每次配对交易可获利：

NPi,j=s·(εto-εtc)≥s·k·δi,j

(5)

因此，本模型设定开仓条件为两配对股票价差偏离均值标准差δ的k倍，即|εto|≥kδi,j；平仓条件为价差回归到均值ui,j时，即εtc=0。本文基于移动平均估计价差趋势，并以拐点作为开仓点。开仓和平仓操作示意图如图2所示。

图2 开仓和平仓示意图

如图2所示，当价差超过(或低于)设定的阈值ui,j+kδi,j(或ui,j-kδi,j)时，发出开仓预警，并跟踪价差走势和移动平均线走势，当发现移动平均线出现拐点时，进行开仓操作，即卖空相对被高估的股票买入被低估的股票；当发现价差向均值回复，向下(或向上)穿过价差均值ui,j时，平掉手中所有仓位，即卖出多头寸买入空头寸。

2.2.4 考虑交易费的CCW策略

s{(1-c)(u+εto)-(1+c)(u+εtc)}=s(1-c)(εto-εtc)

(6)

从上式可见，交易费用会直接降低每次交易的利润。交易费率越高则每次交易获利越低，反之亦然。

2.2.5 融资融券背景下的CCW策略资金分配

理想的配对交易策略是一种自金融(Self Finance)策略，投资者不要资金投入也能够实现盈利：开仓时，先建立空头头寸，用所获资金建立多头头寸；平仓时，先平掉多头头寸，用所获资金购买证券平掉空头头寸。在此种操作下，投资者的资金占用为零，然而，这种“空手套白狼”的操作并不能实现。实际的交易中，投资者需要支付一定的保证金，那么在资金有限约束下，如何才能获取最大的收益呢？根据(4)式可知，建立的头寸s越大获利越多，在资金有限约束下资金使用效率越高。证监会和交易所均规定需维持一定的保证金比例和股票折现率。

假设资金总量为M，配对交易投资组合中多头是股票i，空头是股票j，需建立一个多头头寸L和空头头寸S。在现行保证金制度下，构建一个配对交易的可行方案是：先买入部分股票i(设购买量为α)，用买入股票i和剩余现金量M-α作为抵押，融资买入股票i的量为L-α，融券卖出S的股票j。此种情况下，外生参数为现金买入股票的折现率DR，保证金比例IR，维持保证金比例MR[15]。上述问题可转化为线性规划问题，以最大化多头和空头头寸：

(7)

其中，约束(a)涉及保证金比例要求，约束(b)涉及维持保证金要求，约束(c)确保第一次购买股票量不超过多头头寸量；约束(d)保证购买股票量满足资金约束；约束(e)依据CCW对冲策略。求解上述规划问题，可得出购买股票i的多头头寸L*和组合头寸P*为：

P*=g·L*

(8)

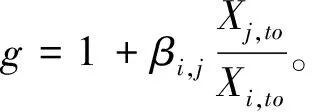
P*=g′·L*

(9)

3 实验设计

3.1 数据描述

本文以上证50指数成分股日度收盘价作为数据样本，并采用向前复权方法进行数据预处理，时间区间为2010年3月1日到2014年9月24日，剔除节假日，共计1090个样本点。特别的，起始日为我国融资融券业务正式实施日期。上证50股票具有市场规模大、流动性好的特点，能够综合反映上海证券市场中具有影响力的龙头企业的整体经济概况。由于上证50指数成分股的样本不断变化，本研究选用2014年12月29日的成分股，并剔除数据不完整的股票，共剩下37只股票，见表1。

表1 本文配对交易研究中的候选股票

根据模型设计，配对交易策略分为配对阶段和交易阶段。设配对阶段的时间长度为TF，交易期的时间长度为TT，总的样本长度为T，采用滚动测试法，则共有m=[(T-TF)/TT]个形成期和交易期对新模型进行检证。

3.2 基准模型

为检验新的两阶段模型的有效性，本文引入基于协整的单模型为基准模型。单模型股票对的选择标准是协整检验中的p值，以p值最小为依据选择股票对的思路如下：

(1)对所有股票进行两两协整检验，记录p值；

(2)选择p值最小的股票对，作为配对股票；

(3)从股票池中删除已配对的股票；

(4)重复(1)-(3)，直至股票池中无股票或剩下的股票对协整检验p值大于0.05。

与本文的设计的模型相比，基准模型选择出的配对股票只满足协整关系，但其欧氏距离并不一定最小。

4 实证结果

4.1 参数设定

模型中的主要参数包括配对阶段的时间长度TF，交易阶段的时间长度TT，触发交易的阈值倍数k。文献中对一般设定配对期的长度为一年，交易的长度为六个月[8]，而在协整模型中，触发交易的阈值倍数k一般设定为2-4之间的数值[3]，本文初始设定k值为2.5，后面的内容将对这些模型参数的敏感性进行分析。通过反复的尝试确定了合适的移动平均线滞后期天数Lag。假设初始投入资金M，交易费率c，融资融券费用f， 融资融券中折现率DR，保证金比例IR和维持保证金比例MR。这些数据的取值与实际的券商操作数据相近[23]。具体的参数设定见表2。

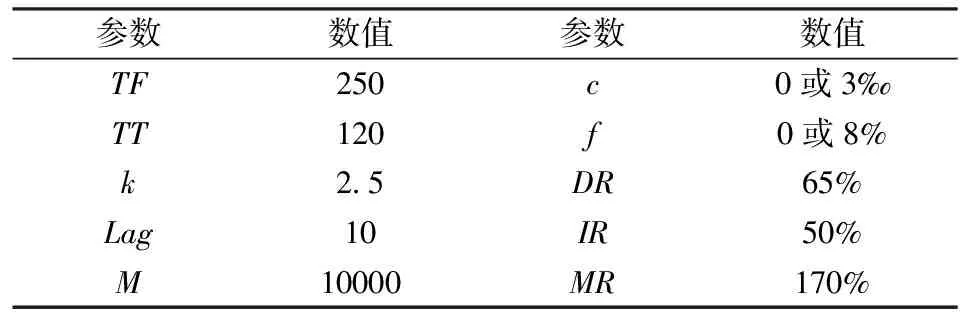
表2 模型参数设定

需要说明的是，每期获利资金将直接作为下期交易本金，进行滚动投资。每个交易期的期初，需计算出配对股票对对数nt和投入本金Mt，平均分配资金，即每组股票对的预算资金为Mt/nt。

4.2 实验结果

在不同交易费用和融资融券费用下，新的两阶段模型与其基准单模型的收益结果如表3所示。从结果可知，与基准模型相比，新的两阶段模型在收益率、夏普比、最大回撤等指标上均显示出显著的优势，表明本文提出的两阶段配对交易模型优于单模型，能有效克服单模型的不足，提高单模型的配对交易收益。例如，以情形4为例，收益方面，新模型的日均收益、年化收益和累计收益率分别为0.02%、5.49%和1.13，均优于单模型的0.00%、1.49%和1.03；考虑风险的收益，新模型的年化夏普比为0.13优于单模型的-0.18；但是，日均收益率波动率、最大回撤率、收益率为负的比例方面，新模型略次于单模型。

在交易费用方面，结果表明费用的增加将降低整体收益。例如，两阶段模型获得的年化收益率在不考虑费率时为10.14%(情形1)，而考虑费率后降为5.49%(情形4)。再次，费用增加还会加大策略的风险。两类模型的日均收益标准差随着费率的增加而有小幅上升，最大回撤、收益为负的比例等呈上升趋势。

为进一步分析两阶段模型的收益分布，图3给出了不同费率情况下的日均收益率分布。从收益率分布来看，四种情况下的偏度均为正值，表明该策略正收益的情况较多。具体的，四种情况下峰度均在18.8左右，大于正态分布峰度值3.0，表明该策略下的收益仍然表现出“尖峰厚尾”的特征[19]。经计算，这些收益率与同期上证50指数收益率的beta值分别为-0.07%、-0.06%、-0.21%和-0.21%，均接近于零，表明新策略能够有效规避市场风险。

两阶段配对交易策略的累计收益率见图4。从图可知，所构建的两阶段配对交易策略累计收益率波动上升，表明该策略具有较高的盈利能力和规避市场风险的能力。

图3 不同费率情形下两阶段模型日均收益分布

图4 费用不同情况下两阶段模型累计收益率走势

4.3 敏感性分析

配对交易策略结果受各参数设定的影响，如配对期数TF和交易期数TT，开仓价差偏离均值的阈值倍数k。在考虑交易费用和融资融券费用的情况下(情形 4)，本文接下来分析模型中这些参数对策略盈利的影响。

表3 两阶段配对交易模型和基准单模型结果比较

首先，考查配对期数和交易期数的选择对收益结果的影响[21]。本文采用网格法探讨最佳TT和TF[14]，其中TF变化范围为60-480天，TT变化范围为30-240天，步长均为30天。统计不同参数设计下年化收益率和最大回撤率，分别如图5与图6所示。

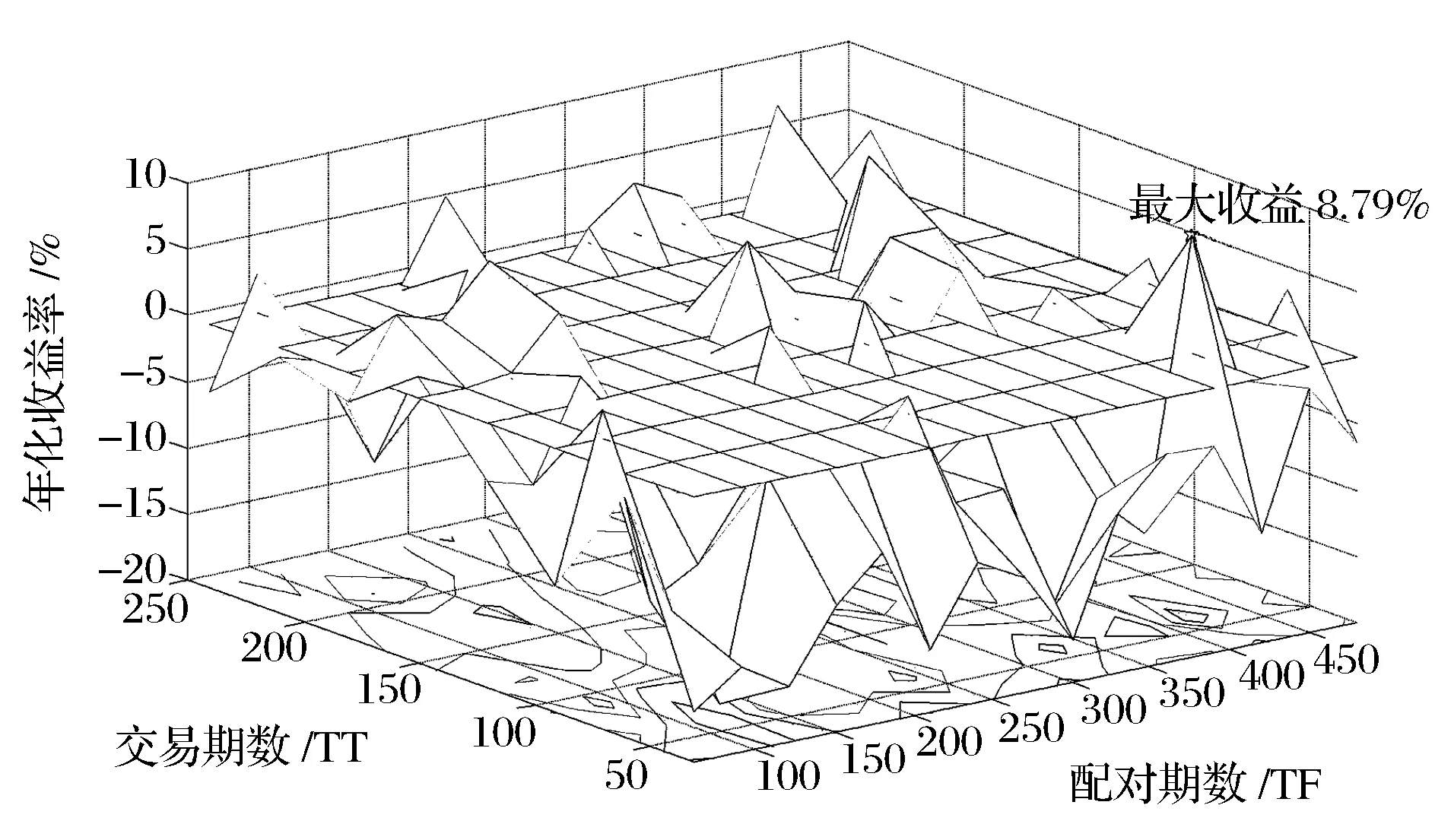
图5 不同配对期数和交易期数设定下两阶段模型年化收益率

由图5可知，收益结果对交易期数TT的反应较对配对期数TF更为敏感。正的收益率多集中在交易期数大于60天的情况，而当TT小于60天时的收益多为负值。主要原因是，交易期太短会导致强行平仓的次数增多，以致每次交易获利不能覆盖交易费用。另一方面，收益率对配对期数TF敏感性较低，在不同的TF取值下，模型都有可能获得正收益，这无疑验证了新两阶段方法能够在不同时间跨度上较好识别出具有长期协整走势的股票对。

图6 不同配对期数和交易期数设定下的最大回撤率

图6展示了不同配对期和交易期数设定下的最大回撤率走势，以反映模型整体风险。结果表明，最大回撤率对交易期数TT的反应相比对配对期数TF更为敏感的特性，与图 5结果相似。当TT的值大于100天时，最大回撤率处于较低水平；当TT值小于100天时，最大回撤迅速增大。这表明该配对策略应该适当选择交易期的长度TT。

此外，参数阈值倍数k同样是模型的关键参数，如果选取太小难以区分出价差是正常波动还是偏离长期均衡，选取过大会降低交易次数从而错过盈利机会[6]。敏感性分析固定其他参数不变，将k值在[0.25,8.00]区间内变化，步长为0.25，比较每种设定下新模型的盈利能力，结果如图7。

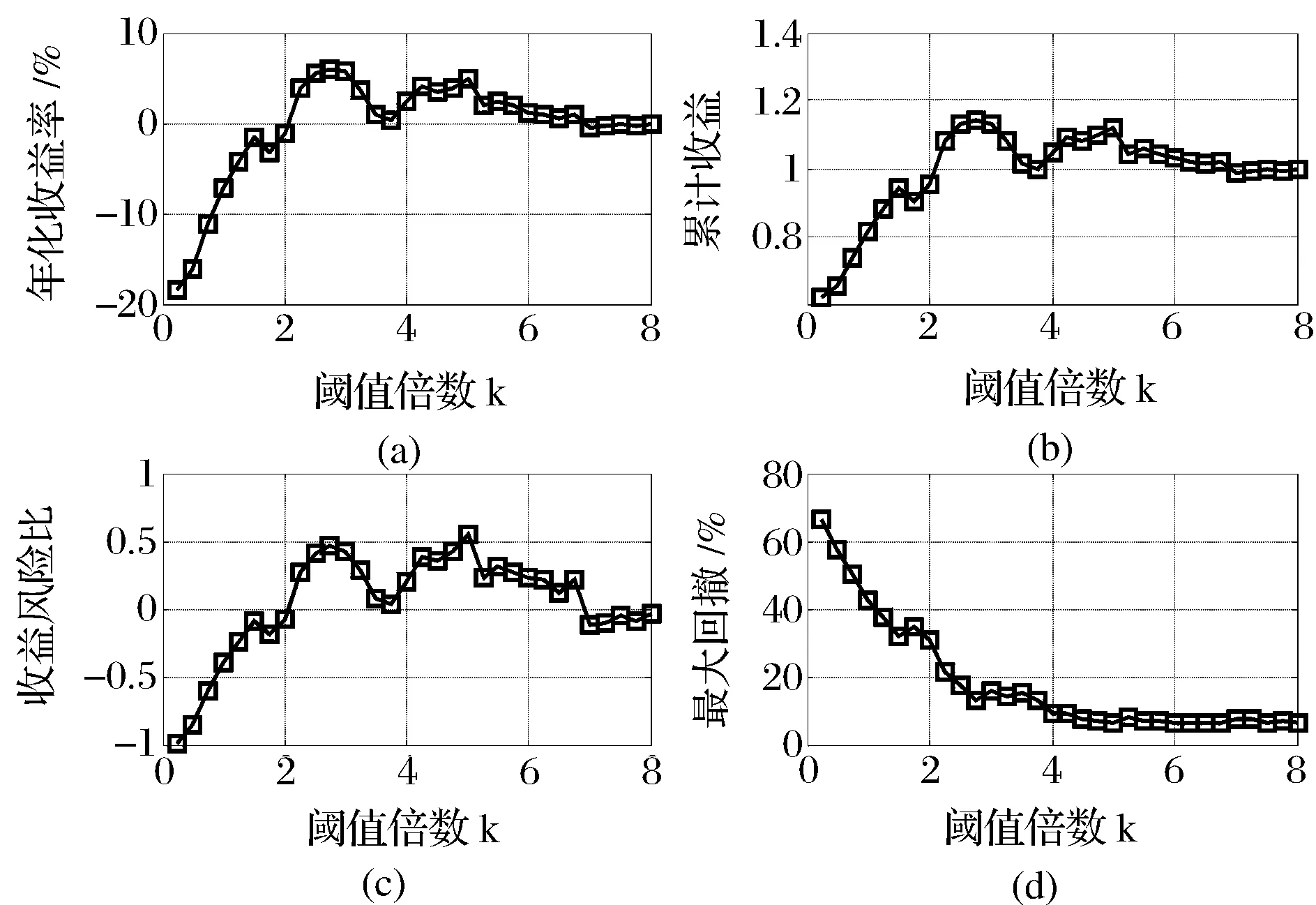
图7 不同阈值倍数设定下两阶段模型表现

由图7可知，新模型的年化收益率、累计收益率和夏普比均先随着阈值倍数k值上升而上升，而后随着k值的增加而下降。特别的，当k值处于2.5至5.0间时，模型表现最为良好，能够取得较高的年化收益率、累计收益率和夏普比。而另一方面，最大回撤率指标却随着k值的增加单调递减，主要原因是阈值倍数k的增加会使每次收益增加，降低亏损的风险，从而最大回撤率降低；同时，k值的增加将降低交易次数，过大的k值会使得整体收益下降。因此，模型应将k值设定在有效的区间内，以保证其盈利能力。

4.4 小结

通过上述分析，可得到以下两个重要结论。(1)与基准模型相比，新的两阶段模型显示出显著的优势，其收益更高而风险更小。这表明本文提出的两阶段配对交易模型优于单模型，能有效克服单模型的不足，提高单模型的配对交易收益。(2)模型收益对参数具有一定的敏感性，建议交易期数设定不宜过短，而阈值应设定于一定的有效区间内。

5 结语

在融资融券的制度环境下，本文构建了基于协整和距离方法的两阶段系数中性配对交易策略，并以上证50成分股指数为实证对象，检验了新方法的可行性与有效性。结果表明，新的两阶段配对策略优于仅考虑协整关系的单模型，能够获得更高的收益和降低模型风险；同时，参数的敏感性分析表明，模型收益对参数的选择具有一定要求，交易期数不宜设定过短以保证价差均值回复获利，阈值选取应当适中，以获取最大收益。然而，为获取更好的模型表现，新模型仍需进一步改进，例如风险控制方面引入止损、加入风险管理目标等;价差预测方面考虑股票行为[18]、投资者情绪[22]、股票间的网络结构[25]等。

[1] Alexander C, Dimitriu A. The cointegration alpha: Enhanced index tracking and long-short equity market neutral strategies [R]. Discussion Paper,ISMA Centre, 2002.

[2] Alexander C, Giblin I, Wayne W. Cointegration and asset allocation: A new active hedge fund strategy [J]. Research in International Business and Finance, 2002,16: 65-90.

[3] Bogomolov T. Pairs trading in the land down under[C]//proceedings of the Finance and Corporate Governance Conference, Bundoora, Australia, 2011.

[4] Do Binh R F, Kais Hamza. A new approach to modeling and estimation for pairs trading[R].Working Paper, Monash University, 2006.

[5] Elliott R J, Van Der Hoek J, Malcolm W P. Pairs trading [J]. Quantitative Finance, 2005, 5(3): 271-276.

[6] Ehrman D S. The handbook of pairs trading: Strategies using equities, options, and futures [M].New York: John Wiley & Sons, 2006.

[7] Engle R F, Yoo B S. Forecasting and testing in co-integrated systems [J]. Journal of econometrics, 1987, 35(1): 143-159.

[8] Gatev E, Goetzmann W N, Rouwenhorst K G. Pairs trading: Performance of a relative-value arbitrage rule [J]. Review of Financial Studies, 2006, 19(3): 797-827.

[9] Gillespie T, Ulph C. Pair trades methodology: A question of mean reversion[C]//Proceedings of International Conference on Statistics, Combinatorics and Related Areas and the 8th International Conference of Forum for Interdisciplinary Mathematics, NSW, 2001.

[10] Hong G, Raul S. Pairs-trading in the Asian ADR market [R].Working Paper, University of Houston, 2004.

[11] Lin Yanxia, McCRAE M, Gulati C. Loss protection in pairs trading through minimum profit bounds: A cointegration approach [J]. Journal of Applied Mathematics and Decision Sciences, 2006：1-14.

[12] Miao G J. High frequency and dynamic pairs trading based on statistical arbitrage using a two-stage correlation and cointegration approach [J]. International Journal of Economics and Finance, 2014, 6(3): 96-110.

[13] Nath P. High frequency pairs trading with us treasury securities: Risks and rewards for hedge funds [J]. Available at SSRN eLibrary, 2003.

[14] Nakagawa T, Iwahori Y, Bhuyan M. Defect classification of electronic board using multiple classifiers and grid search of SVM parameters [M]//Lee R. Computer and Information Science. Springer.International Publishing, 2013: 115-127.

[15] Puspaningrum H. Pairs trading using cointegration approach [D]. Wollongong; University of Wollongong, 2012.

[16] Vidyamurthy G. Pairs trading: Quantitative methods and analysis [M]. New York:John Wiley & Sons, 2004.

[17] 仇中群, 程希骏. 基于协整的股指期货跨期套利策略模型 [J]. 系统工程, 2008, 26(12): 26-29.

[18] 蒋翠清, 梁坤, 丁勇,等. 基于社会媒体的股票行为预测[J]. 中国管理科学, 2015,23(1): 17-24.

[19] 金恺. 基于协整方法的沪深 300 成分股配对交易研究 [D].杭州：浙江大学, 2013.

[20] 麦永冠, 王苏生. WM-FTBD 配对交易建仓改进策略及沪深港实证检验 [J]. 管理评论, 2014, 26(1): 30-40.

[21] 邵超, 范宏. 时间参数的设定对配对交易收益率的影响 [J]. 经济管理学刊: 中英文版, 2013, 2(5): 183-188.

[22] 王春. 投资者情绪对股票市场收益和波动的影响-基于开放式股票型基金资金净流入的实证研究[J]. 中国管理科学, 2014,22(9): 49-56.

[23] 徐沐霖. 基于协整的配对交易研究 [D].济南：山东大学, 2013.

[24] 朱少醒, 张则斌, 吴冲锋. “羊群效应” 与股票收益分布的厚尾特性 [J]. 上海交通大学学报, 1999, 4(7): 40-43.

[25] 张来军, 杨治辉, 路飞飞. 基于复杂网络理论的股票指标关联性实证分析[J]. 中国管理科学, 2014,22(12): 85-92.

Pairs Trading Strategy Research Considering Short Selling and Margin Trading: A Two-Stage Approach Based on Cointegration and Distance Methods

HU Lun-chao1, YU Le-an2, TANG Ling2

(1. Academy of Mathematics and Systems Science,Chinese Academy of Sciences, Beijing 100080,China;2.School of Economics and Management, Beijing University of Chemical Technology, Beijing 100029, China)

China has established the policy of short selling and margin trading, which enables the pairs trading strategy to be a promising tool for financial investment. This study tries to formulate a two-stage pairs trading strategy based on cointegration method and distance estimation. In particular, the cointegration approach is applied to all possible pairs of stocks to check the potential cointegration relationship, and the distances of the pairs with cointegration relationship are measured to finally determine the optimal pairs with minimum distances. Furthermore, the optimal pairs portfolio is given weighted by cointegration coefficients under finite investment budget, considering short selling and margin trading. To verify the effectiveness of proposed approach, the Shanghai 50 Index stocks are used as study samples. Empirical results show that the novel two-stage model outperforms the benchmark model only considering cointegration relationship, in term of excess returns. Besides, the sensitivity analysis confirms the robustness of the model.

portfolio; pairs trading; cointegration analysis; distance estimation; short selling and margin trading

1003-207(2016)04-0001-09

10.16381/j.cnki.issn1003-207x.2016.04.001

2015-03-01；

2015-05-26

国家杰出青年科学基金资助项目(71025005)

汤铃(1983-)，女(汉族)，广西桂林人，北京化工大学经济管理学院，副教授，研究方向：商务智能、数据控掘、仿真模拟、能源经济等，E-mail:tangling@mail.buct.edn.cn.

F224.7

A