分步动态自回归核主元分析及其在故障诊断中应用

张敏龙 王涛 王旭平 常红伟 王放

摘要：针对滑动窗自适应核主元分析法（KPCA）在处理参数敏感和缓慢劣化问题时存在的“过适应”现象，容易产生漏报的问题，提出了一种分步动态自回归KPCA算法。首先，借鉴动态数据矩阵思想，分步建立初始模型；然后，在滑动窗自适应KPCA的基础上，引入指数加权法则处理实时数据、更新模型；最后，分析算法复杂度，并给出具体实现步骤。利用模拟数据分析分解系数和加权因子对算法的影响，结果表明，与滑动窗自适应KPCA相比，所提方法在参数选择恰当的情况下，模型效率提高了近90%，误报次数几乎降为0，还能通过调整加权因子取值来控制算法的适应能力，以解决多样化的动态问题。将算法应用于压缩机喘振和轴承故障实验数据分析，验证了所提算法处理参数敏感和缓慢劣化问题的能力。

关键词：核主元分析；滑动窗；分步动态策略；指数加权；故障诊断

中图分类号：TP277 文献标志码：A

Abstract：There are overfitting phenomenon and prone omissions when moving window adaptive Kernel Principal Component Analysis （KPCA） is utilized to deal with sensitive parameters or slow degradation problem. In order to solve the problem， a step dynamic autoregression KPCA was proposed. Firstly， the initial model was established step by step drawing on dynamic data matrix. Then， the exponentially weighting rule was introduced to process realtime data and update the model based on the moving window adaptive KPCA. Finally， the algorithm complexity was analyzed and specific steps were given. The simulation data was utilized to analyze the impact of decomposition coefficient and weighting factor. The results show that， compared with the moving window adaptive KPCA， the proposed algorithm efficiency was improved by nearly 90% and the number of false positives was almost 0 in the case of appropriate parameter selection； and it could also control the adaptive ability to solve a variety of dynamic problems by adjusting the value of weighting factor. The algorithm was applied to the experimental data analysis of compressor surge and bearing fault， the result verified its ability to deal with the problem of sensitive parameter and slow degradation.

Key words：Kernel Principal Component Analysis （KPCA）； moving window； step dynamic strategy； exponentially weighting； fault diagnosis

0 引言

Schlkopf等[1]提出的核主元分析法（Kernel Principal Component Analysis， KPCA）是一种非线性数据处理方法，目前已经在入侵检测、图像处理、过程监控、故障诊断等领域得到了成功应用[2-5]。但传统KPCA建立在静态模型的基础上，存在模型训练完成后不能改变的缺陷，应用于动态时变系统中可能会出现大量误报、漏报问题。

为此，近年来研究者们相继提出了一些动态KPCA方法。文献[6]结合滑动窗机制提出了一种自适应动态KPCA方法，使模型能够适应时变系统的参数漂移，并成功应用于航空发动机的故障动态监测中。该方法实时性好、自适应性强、模型更新周期可控，适用于跟踪设备正常状态的漂移，同时能够减少误报的发生。但该方法刻板地使用实时数据替换原始数据，缺少对适应性的控制，在推广到处理设备参数敏感和缓慢劣化问题时会出现“过适应”，影响算法效果，存在漏报的可能。

针对上述问题，本文借鉴文献[7]的动态数据矩阵思想，在滑动窗自适应KPCA的基础上，引入文献[8]的指数加权法则，提出一种分步动态自回归核主元分析法（Step Dynamic AutoRegression KPCA，SDAR_KPCA）。该方法首先将训练样本分解扩展，分两步提取数据的相关关系，减小核矩阵规模和计算复杂度；然后根据动态数据，加权更新核矩阵，调节加权因子以适应不同类型动态系统的要求，降低误报、漏报概率；最后利用模拟数据验证算法的快速性和自回归性，并将算法应用于压缩机喘振过程信号和IMS（Intelligent Maintenance System）轴承故障实验数据的分析。

1 分步动态自回归核主元分析法

1.1 算法基本思想

文献[7]指出，对于动态系统，实时观测数据与过去时刻观测数据是紧密联系的，利用静态KPCA模型难以获取数据之间的相关关系，并针对这一问题提出分步动态策略：首先对数据样本在时间方向上进行扩充，构造数据增广矩阵，然后利用核主元分析提取数据的空间相关关系，最后利用主元分析（Principal Component Analysis，PCA）提取数据的时间相关关系，分两步获取动态数据之间的相关性。

滑动窗机制利用实时采集的正常样本替换相同数量的原始样本，重新生成正常样本集，建立新模型进行检测，以达到控制模型更新频率和适应实时数据变化的目的。对滑动窗数据使用分步动态策略，记滑动窗宽度为ω，滑动步长为s，当前窗口数据为{xi}ωi=1∈Rm，定义分解系数为D，利用当前窗口样本数据构建增广矩阵X（D）：

按列分解矩阵X（D），再先后进行KPCA和PCA分析，建立模型。滑动窗每次以步长s向前滑动，依次在各窗口更新模型。然而滑动窗机制刻板地使用实时数据替换原始数据，没有考虑原始数据信息，在模型多次更新后，可能会出现偏离现象，增大误报、漏报几率。更糟糕的是，在处理对象参数敏感或设备缓慢劣化问题时，滑动窗自适应KPCA对动态数据变化适应过度，会出现类似于“过学习”的现象，以至于无法准确辨别这两类问题的发生。

其中γ∈[0，1]表示加权因子。γ的大小在模型更新时刻画了算法对不同时刻数据样本的重视程度，也反映了对实时样本的适应能力。可以根据不同问题要求，选取合适的γ，以满足相应的诊断目的。

1）γ越大，则原始样本具有较大权重，表示算法越重视原始样本，对实时样本的适应能力越弱。特别地，当γ=1时，表示未对核矩阵进行更新，也就是不更新模型样本数据，没有适应能力，相当于静态KPCA。对于参数敏感的问题，适合选择较大的γ，当动态系统参数一旦发生漂移，就能够被及时察觉。

2）γ越小，则新样本具有较大权重，表示算法越重视实时样本，对实时样本的适应能力越强。特别地，当γ=0时，表示核矩阵直接更新，没有使用原始数据进行加权，相当于滑动窗自适应KPCA。对于设备缓慢劣化的问题，应尽量选择较小的γ，使算法具有较强的适应能力，在一定范围内适应设备参数的漂移，γ的具体取值视设备状态变化特点而定。

1.2 算法步骤

1）离线训练。

步骤1

收集正常样本集X，用于初始KPCA模型的建立。设定分解系数D，滑动窗宽度ω，滑动步长s，加权因子γ，累计数k置零。计算窗口数据的均值和标准差，并进行标准化处理。

步骤2

2 仿真与应用分析

2.1 仿真分析

设备运行时往往会发生状态漂移，根据设备类型、工作环境、应用场合等不同，会将不同程度的状态漂移情况视为故障。为方便描述，本文使用一维模拟数据进行仿真分析，该数据以正态分布的随机信号为基础，通过调整均值和标准差，模拟设备从正常状态到出现漂移直至劣化的过程，如图1所示，把漂移过程的任何位置都认为是可能的故障起始点。

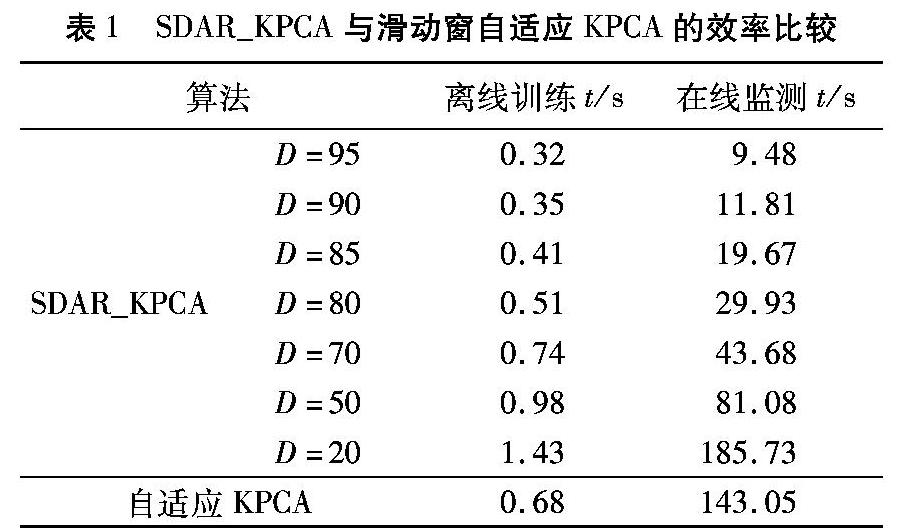
由表1可以看出，SDAR_KPCA的离线训练用时与滑动窗自适应KPCA相比并无明显优势，在分解系数D小于80后，训练时间甚至比滑动窗自适应KPCA还长。但从在线检测更新时间上看，使用较大的分解系数时后，本文算法耗时远小于滑动窗自适应KPCA，而且D越大，更新时解算的核矩阵规模就越小，耗时也就越短，说明SDAR_KPCA算法能够提高模型更新效率。

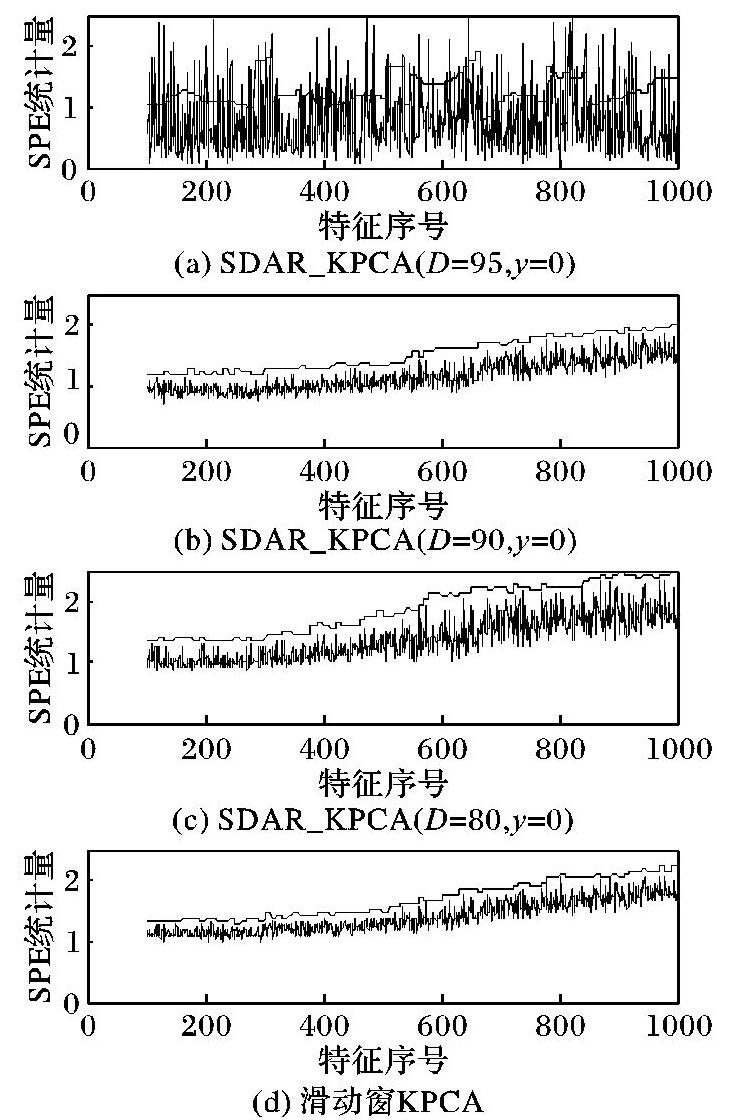
图2自上而下分别是SDAR_KPCA在D取95、90、80时以及滑动窗自适应KPCA的SPE统计量监控结果。由图2可见，SDAR_KPCA算法在D取90或80时，和滑动窗自适应KPCA一样，统计量能适应数据的漂移；但当SDAR_KPCA分解系数D取95时，SPE的监控结果很不理想，这是由于分解后每个子矩阵的训练样本数过少，导致不能从统计意义上构成协方差矩阵，进而影响了模型的监测效果， 因此，选取分解系数D时要综合考虑快速性和准确性的影响，在不影响准确性的情况下，让D尽量接近滑动窗宽度ω的值。

2.1.2 自回归性验证

固定分解系数D=90，然后令SDAR_KPCA取不同加权因子γ进行在线监测。图3（a）～（c）分别是γ取0.2、0.8和1时的SPE监控结果，表2记录了部分γ取值的SPE超限位置以及状态漂移前的误报次数。

从图3和表2可以看出，γ取值越小，SPE统计量的超限位置越靠后，算法对状态漂移的适应能力越强，在γ接近于0时，统计量甚至不会越限。随着γ取值不断增大，SPE超限位置前移，特别是γ接近于1时，数据状态一发生漂移，统计量就会越限。说明SDAR_KPCA模型能够保留原始数据信息，具有自回归性，而且可由γ的大小控制模型的适应能力，使之对不同问题具有适用性。

另外，当γ取值过大时，状态漂移前就出现了少量误报问题，这是由于模型不更新或更新时新样本的权值太小所引起的，此时SDAR_KPCA的性能退化至与静态KPCA相当。

2.2 应用分析

下面，利用SDAR_KPCA分别对两种不同类型的实际故障数据进行分析。

1）压缩机喘振过程信号分析。

分析250kW单级离心压缩机从正常到喘振的发展过程，实验转速为13570rpm，采样频率为150Hz，采样点数为2048，调节节流阀让压缩机发生喘振，得到进口总压和出口静压信号如图4所示[10]。

喘振现象对离心压缩机危害巨大，必须对喘振先兆作出及时准确辨别，一旦发生参数漂移就能立即报警，属于参数敏感问题，所以选择较大的γ。将压力信号合成二维数据，选取滑动窗宽度ω=200，分解系数D=180，滑动步长s=10，核参数σ=5m/2=2.24，主元控制限为0.85，统计量控制限的置信度为99%，图5显示了加权因子γ=0.9时SPE的监控结果。

图5表明，在压缩机平稳运行时，SPE未出现超限情况，在压缩机进出口压力参数发生漂移瞬间，SDAR_KPCA模型及时给出了报警信息，实现了喘振先兆的准确识别。但是，报警后出现了大量“漏检”点，这是由于没有进行特征提取，而样本点的压力信息恰好与正常状态相符引起的。

2）IMS轴承故障实验数据分析。

数据来自美国辛辛那提大学IMS中心的轴承故障实验[11]，实验中4个滚动轴承同轴安装，1#、4#轴承固定在实验台上，2#、3#轴承通过弹簧机构施加6000lb恒定径向负载，转速保持2000rpm，并在每个轴承上设置两个PCB 353B33型振动传感器，分别测量轴承水平和垂直振动信号。

实验从2004年2月12日10：32：29持续到2月19日06：22：39，每隔10min利用NI DAQ 6062E信号采集平台记录各轴承的垂直振动信号，采样频率为20kHz，采样点数为20480，共有984段4维信号数据。计算每段数据的时域统计指标作为原始特征，具体同上节模拟数据的10类指标，共得984点40维特征。选取滑动窗宽度ω=100，分解系数D=90，滑动步长s=10，核参数σ=5m/2=10，主元控制限为0.85，统计量控制限的置信度为99%，图6为加权因子γ分别取0.8和0.2时SPE的监控结果。

当γ=0.8时，SPE在第703点处超出控制限，对该段原始信号进行包络分析，发现1#轴承的状态开始出现漂移，但仍处于正常工作范围。当γ=0.2时，统计量在最后几个特征点处才发生越限，此时的包络谱表明1#轴承的外圈处于故障状态，最后停机检查发现1#轴承外圈存在裂纹。实验记录了轴承外圈缓慢劣化的过程，通过设置较小的加权因子γ如0.2，SDAR_KPCA模型能够准确判断出故障的发生。而设置较大的γ如0.8，则可以识别出状态漂移的起始位置， 因此，可以设置双层甚至多层SDAR_KPCA模型，形成层级报警器，可以得到更精确的诊断结论。

3 结语

本文借鉴分步动态策略，在滑动窗自适应KPCA中引入指数加权法则，提出了SDAR_KPCA算法，利用模拟数据验证了算法效果，并将其成功应用于压缩机喘振故障和IMS轴承故障诊断，主要结论如下：

1）SDAR_KPCA降低了算法复杂度，提高了模型更新效率，在保证准确性的前提下，让分解系数尽量接近滑动窗宽度的值，可以实现动态数据的快速诊断。

2）SDAR_KPCA实现了模型的自回归更新，根据实际问题选择合适的加权因子，调节原始数据和动态数据的权重，能够得到良好的诊断结果。

3）通过设置不同加权因子建立双层甚至多层SDAR_KPCA模型，能形成层级报警器，从而达到更详实诊断的目的。

参考文献：

[1]SCHLKOPF B， SMOLA A， MLLER K R. Nonlinear component analysis as a kernel eigenvalue problem [J]. Neural Computation， 1998， 10（5）： 1299-1319.

[2]余文利，余建军，方建文.一种新的基于KPCA和改进εSVM的入侵检测模型[J].计算机工程与应用，2015，51（11）： 93-98. （YU W L， YU J J， FANG J W. Novel intrusion detection model based on KPCA and improved εSVM [J]. Computer Engineering and Applications， 2015， 51（11）： 93-98.）

[3]LIN C， PENG F， WANG BH， et al. Research on PCA and KPCA selffusion based MSTARSAR automatic target recognition algorithm [J]. Journal of Electronic Science and Technology， 2012， 10（4）： 352-357.

[4]JIANG Q C， YAN X F. Statistical monitoring of chemical processes based on sensitive kernel principal components [J]. Chinese Journal of Chemical Engineering， 2013， 21（6）： 633-643.

[5]张恒，赵荣珍.故障特征选择与特征信息融合的加权KPCA方法研究[J].振动与冲击，2014，33（9）：89-93，121. （ZHANG H， ZHAO R Z. Weighted KPCA based on fault feature selection and feature information fusion [J]. Journal of Vibration and Shock， 2014， 33（9）： 89-93， 121.）

[6]胡金海，李应红，杨帆，等.一种基于自适应核主元分析的故障检测方法[J].控制工程，2007，14（S1）：80-83. （HU J H， LI Y H， YANG F， et al. A fault detection method based on kernel principal component analysis [J].Control Engineering of China， 2007， 14（S1）： 80-83.）

[7]CHOI S W， LEE I B. Nonlinear dynamic process monitoring based on dynamic kernel PCA [J]. Chemical Engineering Science， 2004， 59（24）： 5897-5908.

[8]WOLD S. Exponentially weighted moving principal component analysis and projection to latent structures [J]. Chemometrics and Intelligent Laboratory Systems， 1994， 23（1）： 149-161.【Proceedings of the 3rd Scandinavian Symposium on Chemometrics （SSC3）】

[9]姜万录，吴胜强，刘思远.指数加权动态核主元分析法及其在故障诊断中应用[J].机械工程学报，2011，47（3）：63-68. （JIANG W L， WU S Q， LIU S Y. Exponentially weighted dynamic kernel principal component analysis algorithm and its application in fault diagnosis [J].Journal of Mechanical Engineering， 2011， 47（3）： 63-68.）

[10]张庆. 基于核方法的机械设备动态监测诊断模型与关键技术研究[D]. 西安：西安交通大学， 2007. （ZHANG Q. Research on the dynamical model and its key techniques for condition monitoring and fault diagnosis of mechanical equipments based on kernel methods [D]. Xian： Xian Jiaotong University， 2007.）

[11]LEE J， QIU H， YU G， et al. ‘Bearing Data Set， IMS， University of Cincinnati. NASA Ames Prognostics Data Repository， NASA Ames， Moffett Field， CA [EB/OL]. [2015-07-20]. http：//ti.arc.nasa.gov/projects/data_prognostics/.

[12]QIU H， LEE J， LIN J， et al. Wavelet filterbased weak signature detection method and its application on rolling element bearing prognostics [J]. Journal of Sound and Vibration， 2006， 289（4/5）： 1066-1090.