基于稀疏表示权重张量的音频特征提取算法

林静 杨继臣 张雪源 李新超

摘要：为了更好地描述非平稳音频信号的特征，提出了一种基于Gabor字典和稀疏表示权重张量的时频音频特征提取方法。该方法基于Gabor字典将音频信号编码为稀疏的权重向量，并进一步将权重向量中的元素重新排列为张量形式，该张量各阶分别刻画了信号的时间、频率以及时长特性，为信号的联合时频长表示。通过对该张量进行因子分解，将分解后得到的频率因子和时长因子拼接为音频特征。针对稀疏张量分解时容易产生过拟合的问题，提出一种自调整惩罚参数分解算法并进行了改进。实验结果显示，所提出的特征相对于传统梅尔倒谱系数（MFCC）特征、MFCC特征及匹配追踪算法（MP）求解的特征联合拼接得到的MFCC+MP特征和非均匀尺度频率图特征对15类音效分类效果分别提升了28.0%、19.8%和6.7%。

关键词：稀疏表示；张量因子分解；音效分类；时频特征

中图分类号：TN912.3 文献标志码：A

Abstract：A joint timefrequency audio feature extraction algorithm based on Gabor dictionary and weight tensor of sparse representation was proposed to describe the characteristic of nonstationary audio signal. Conventional sparse representation uses a predefined dictionary to encode the audio signal as sparse weight vector. In this paper， the elements in the weight vector were reorganized into tensor format. Each order of the tensor respectively characterized time， frequency and duration property of signal， making it the joint timefrequencyduration representation of the signal. The frequency factors and duration factors were concatenated as audio features through tensor decomposition. To solve the overfitting problem of sparse tensor factorization， an automaticadjustpenaltycoefficient factorization algorithm was proposed. The experimental results show that the proposed feature outperforms MFCC （MelFrequency Cepstrum Coefficient） feature， MFCC+MP feature concatenated by MFCC and Matching Pursuit （MP） features， and nonuniform scalefrequency map feature by 28.0%， 19.8% and 6.7% respectively， in 15category audio classification.

Key words：sparse representation；tensor factorization；audio effect classification；timefrequency feature

0 引言

传统的语音特征通常从频域或者倒谱域对信号进行表示，这些特征均假定在一短时帧内信号的统计特性平稳，即信号具有短时平稳性。但是这些特征不适用于刻画非平稳的音频信号，例如闪电声和枪声。为了描述统计特性随时间变化的信号，基于稀疏表示（Sparse Representation）的方法受到了广泛的关注。稀疏表示利用一个过完备的字典，将信号编码为一个稀疏的权重向量序列，每个向量中的非零元素值表示了重建时对应原子的权重。有许多文献使用该权重向量进行信号分类。Zubair等[1-2]直接使用该权重向量作为特征进行音频信号分类，并且通过使用最大投票和平均投票等方法提取更为鲁棒的特征。Chu等[3]使用匹配追踪（Matching Pursuit， MP）算法求解稀疏表示，并且利用分解后原子的频率和时长的均值和方差信息作为梅尔倒谱系数（MelFrequency Cepstrum Coefficient， MFCC）特征的补充特征。Sivasankaran等[4]对Chu算法进行了改进，提出使用权重计算加权的频率和时长平均值和方差作为特征。在上述文献中，均使用了原子参数的低阶统计量表征信号的频率和时长分布特性。但是，由于稀疏表示的目的是使用具有区分性的原子表示信号，而计算这些原子的均值和方差则消除了单个原子的表征能力。针对此问题，Wang等[5]提出了非均匀尺度频率图（Nonuniform ScaleFrequency Map）特征提取方法，他们构建了一个频率时长图来保存每个原子的频率和时长参数，将该图向量化后利用主成分分析（Principal Component Analysis， PCA）算法和线性判别式分析 （Linear Discriminant Analysis， LDA）算法对其进行降维，但该方法的主要不足是向量化丢失了二维的信息，以及没有使用对于时变信号分类具有重要作用的时间信息。

本文提出稀疏表示的张量（Tensor）形式，称为权重张量。根据Gabor字典的3个参数，即时间、频率和时长，将权重排列到3阶张量中，权重张量中每一个元素都表示了信号中某个瞬时成分的中心频率、中心时间位置以及持续时长，其中频率、时间以及时长信息通过元素在张量中的索引表示，该瞬时成分的强度通过元素的值表示， 因此该张量是信号的联合时频长表示。该张量表示相比于直接获取特征向量的方法具有可以联合分析信号成分的优势，具体地，张量中加入了信号的时间信息，该时间信息可以描述信号的时变特性，即瞬时成分出现的不同时间位置，该位置对于瞬时信号分类具有重要作用。但是由于其高维和稀疏特性，该张量不适合直接用作特征，因此通过张量因子分解算法将其分解为若干因子向量，并提出了一种自调整惩罚参数的分解算法以避免因子分解的过拟合。本文提出的张量特征通过时频长联合分析保证了张量分析过程中保留了瞬时成分的主要特性，从而得到表征能力更强的频率因子和时长因子。

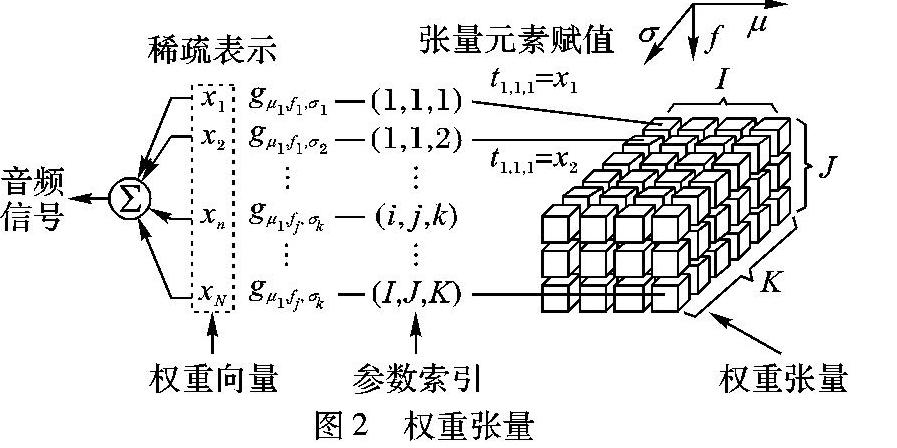
权重向量和权重张量均包含了所有原子的权重信息，只是两者的排列方式不同。张量元素的索引和Gabor参数的索引相一致，每个张量元素需要3个索引值来标示其位置，即时间、频率和时长索引值，因此张量元素的索引表达了Gabor原子参数之间的联合关系。该张量利用其高阶特性来联合地表达了权重与其对应原子的时间、频率和时长参数。此外，由于权重表示了原子的幅度，因此张量是信号的联合时频长表示。例如，张量元素ti， j，k表示信号中在时间μi，一个频率为fj的分量，其时长为σk，强度为|ti， j，k|。

1.3 张量因子分解

张量元素的绝对值表示了信号中瞬变成分的强度。对张量T中每个元素取绝对值得到非负张量|T|。此外，权重张量与权重向量一样均满足稀疏条件，因此|T|为非负稀疏张量。本节中，对该非负稀疏张量进行分解。传统的张量分解算法包括CP（Canonical decomposition Parallel factor analysis）算法和Tucker3算法，这些算法针对的是非稀疏的矩阵，对稀疏矩阵分解时会产生过拟合问题[6]。通常算法会使用l1范数惩罚，通过最小化输出因子的元素的和来避免过拟合[7]，但是该方法没有指明输出因子中的哪些元素应当最小化，因此需要通过多次随机初始化和更新过程寻找最优解。

在本文中，张量中各部分的稀疏度被用作惩罚参数，惩罚它们对应的输出因子元素，因此对于不同的输出因子的元素有不同的惩罚参数。具体地，从张量中稀疏部分分解出的因子元素的惩罚参数大于从张量紧致部分分解出的因子元素，从而使用更多的非零因子元素近似紧致部分，使用少量的非零因子元素近似张量中的稀疏部分，使得在保证分解准确性的前提下避免过拟合。同时，与l1范数的方法相比，由于指定了每个输出因子元素的惩罚值，即指明了哪些因子元素应当最小化，因此可以在更少的循环迭代中收敛。

其中当代价函数值在相邻两次迭代中的相对变化小于一个门限ε时停止迭代。

因子w刻画了数据中显著的频率值，s表示它们的持续时长，u指出其出现的位置，即以帧起始位置为时间原点频率成分出现在帧内的时间位置，但是受到分帧的影响，不同帧之间的u因子不具有共同时间原点，因此在完成联合时频长分解后丢弃该因子，不作为特征。将w和s拼接起来，通过LDA降维后作为特征。

2 实验和结果

2.1 权重张量

本文采用正交匹配追踪算法（Orthogonal Matching Pursuit， OMP） [9]进行信号的稀疏表示分解。字典原子参数集设置如下μ∈{1+32m：0≤m≤15，m∈Z}， f∈{0.5×（m/25）2.6：1≤m≤25， m∈Z}， σ∈{2m：3≤m≤11，m∈Z}， 因此权重张量的维数是16×25×9，经过LDA降维后的特征向量维数为13。

一短时帧的女性语音和河流流水声分别如图4（a）和（b）所示，其权重张量分别如图4（c）和4（d）所示，其中稀疏表示原子数目选择为32。图中尺寸较大的点表示权重较大的值，反之，尺寸较小的点表示较小的权重值，权重为0的元素没有显示。如图4（c）中可见一个尺寸较大的点，该点的索引为（9，12，6），根据原子参数取值该点的中心位置为257个采样点，频率为0.074（即1186Hz），时长为256个采样点，因此该点表示了在该语音帧中的一个能量集中的频率分量。与之相比，图4（d）中的点能量均相似，且能量普遍较小，与河流流水无显著频率成分的事实相一致。对比图4（e）、（g）与图4（f）、（h）可以看出，语音的中心频率集中在一个因子元素上，而河流流水声相对较为分散；此外，两者时长因子的分布模式也有较大不同。

2.2 音效分类实验结果

本文使用15类音效分类任务评估所提出的特征，音效包括男性语音、女性语音、婴儿语音、掌声、脚步声、鸟叫声、猫叫声、河流流水声、雷声、引擎声、枪声、警报声、钢琴声、小提琴声和鼓声。所有音效都是从Digital Juice音效库Ⅰ和Ⅱ[10]以及BBC（British Broadcasting Corporation）音效库[11]中收集的，所有音效样本时长介于3～8s，单声道，16kHz采样，使用32ms帧和8ms帧移。

高斯混合模型（Gaussian Mixture Model，GMM）对于该多分类问题有最好并且最稳定的分类结果[3]，因此本文统一采用该分类器对各组特征进行分类实验比较。GMM的混合度为8，惩罚参数α、 β和γ通过最优化男性和女性语音的二分任务设定为0.132、0.109和0.097。门限ε根据经验设定为0.01。在Matlab 7.14.10仿真平台下将本文所提出的13维张量特征（Tensor）与13维MFCC特征、MFCC特征和匹配追踪算法稀疏分解的MP特征拼接得到的17维联合 MFCC+MP特征[3]、16维非均匀尺度频率图特征（Map）[5]比较分类效果。此外，为了验证所提出的自调整惩罚参数分解算法的有效性，Tensor特征还与CP分解算法（CP）和l1范数惩罚的CP算法（l1CP）进行比较。

每种特征对所有音效类的平均分类效果如图5所示，每一类的识别率定义为正确识别为该类的样本数与该类总样本数的比值，所有类的平均识别率通过10折交叉验证得到。由于稀疏表示中稀疏度的不同会导致识别率不同，因此选择以2为底的对数尺度的原子数目进行稀疏表示，分别测定不同原子数目下的识别效果。Tensor特征、非均匀尺度频率图特征和MFCC+MP特征对每一音效类的识别率如图6所示。注意，图6中每种特征对应的原子数是根据图5中该种特征达到最高识别率时的原子数决定的。

最好的平均识别率时由Tensor特征在原子数为128时得到的84.8%，非均匀尺度频率图Map特征的平均识别率在原子数为64时取得最高，为77.6%。此外，Tensor特征在原子数目为16～256时识别率均高于83%，因此该特征对原子数目具有鲁棒性。在各原子数目下，Tensor特征分类效果均优于非均匀尺度频率图特征，原因在于Tensor特征相比于非均匀尺度频率图特征多使用了时间信息进行联合分析，而时间信息对于瞬变信号分类具有重要作用。该结论也可以从图6中看出，其中，与非均匀尺度频率图特征相比，Tensor特征显著提升了河流流水声，雷声，引擎声和枪声的分类效果，此外，对人类语音、掌声和脚步声也均有一定提升。MFCC+MP特征最高的识别率时8个原子数对应的64.6%。Tensor特征较非均匀尺度频率图特征、MFCC特征和MFCC+MP特征识别率分别高出6.7%、28.0%和19.8%。

3 结语

本文以音效分类为应用背景，提出了一种基于稀疏表示权重张量的特征提取方法，刻画了音频信号中瞬变成分的特性。Gabor原子的时间、频率以及时长特性用来建立一个张量，描述了信号的联合时频长分布特点。该张量刻画了信号更多具有区分力的特性，并且利用张量分解得到描述信号短时帧内频率分布的频率因子和时长分布的时长因子。该张量结构和因子分解过程相比于直接进行向量特征提取的方法描述了更多信号的区分特性。此外针对稀疏张量分解还提出了一种自调整惩罚参数分解算法，利用张量的稀疏度动态作为惩罚参数，有效避免了过拟合。实验结果显示，所提出的张量特征对15类音效的分类效果显著优于其他特征。

参考文献：

[1]ZUBAIR S，WANG W. Audio classification based on sparse coefficients[C]// Sensor Signal Processing for Defence （SSPD 2011）. London， UK： The Institution of Engineering and Technology Press， 2011：1-5.

[2] ZUBAIR S， YAN F， WANG W. Dictionary learning based sparse coefficients for audio classification with max and average pooling[J]. Digital Signal Processing， 2013， 23（3）：960-970.

[3] CHU S， NARAYANAN S，KUO C C J. Environmental sound recognition with timefrequency audio features[J]. IEEE Transactions on Audio， Speech， and Language Processing， 2009， 17（6）：1142-1158.

[4] SIVASANKARAN S， PRABHU K M M. Robust features for environmental sound classification[C]// Proceedings of the 2013 IEEE International Conference on Electronics， Computing and Communication Technologies. Piscataway， NJ： IEEE， 2013：1-6.

[5] WANG J C， LIN C H，CHEN B W， et al. Gaborbased nonuniform scalefrequency map for environmental sound classification in home automation[J]. IEEE Transactions on Automation Science and Engineering， 2014，11（2）：607-613.

[6]TAKEUCHI K， ISHIGURO K， KIMURA A， et al. Nonnegative multiple matrix factorization[C]// Proceedings of the 23rd International Joint Conference on Artificial Intelligence. Beijing： AAAI， 2013： 1713-1720.

[7]LIU J， LIU J， WONKA P， et al. Sparse nonnegative tensor factorization using columnwise coordinate descent[J]. Pattern Recognition， 2012， 45（1） ：649-656.

[8]CICHOCKI A， ZDUNEK R，PHAN A H， et al. Nonnegative Matrix and Tensor Factorizations： Applications to Exploratory Multiway Data Analysis and Blind Source Separation[M]. New York： John Wiley & Sons， 2009：35-37.

[9]CHANG L H， WU J Y. An improved RIPbased performance guarantee for sparse signal recovery via orthogonal matching pursuit[J].IEEE Transactions on Information Theory， 2014， 60（9）：5702-5715.

[10]Digital Juice， Incorporated. The digital juice sound FX library[DB/OL].[2015-05-20]. http：//www.digitaljuice.com.

[11]British Broadcasting Corporation （BBC）.BBC sound effects library[DB/OL]. [2015-05-20]http：//www.soundideas.com/bbc.html.