改进的基于AVS2的样点自适应补偿滤波算法
2016-05-14陈智贤王国中赵海武李国平滕国伟
陈智贤 王国中 赵海武 李国平 滕国伟

摘要:样点自适应补偿(SAO)是第二代数字音视频编解码标准(AVS2)和高效视频编码(HEVC)标准中环路滤波耗时较多的一部分。针对现有自适应样点补偿算法计算量大、复杂度高等问题,提出一种改进的快速率失真算法。该算法主要通过分析各个边缘模式下不同补偿值的变化与所对应的率失真变化之间的关系,对原本定义的补偿值与写入码流的二元符号串之间的关系表进行修改,在不需要计算每个补偿值的率失真代价的情况下,设定一个提前终止条件,快速找到当前样值偏移补偿单元最优的补偿值。实验结果表明,与AVS2下的计算结果相比,在保证图像率失真基本不变的前提下,改进的算法减少了寻找最优补偿值的计算量以及75%的循环次数和33%的环路滤波运行时间,从而降低了计算的复杂度。
关键词:第二代数字音视频编解码标准;高效视频编码;样点自适应补偿;边缘模式补偿值;率失真代价
中图分类号:TN919.81 文献标志码:A
Abstract:Sample Adaptive Offset (SAO) is a timeconsuming part of inloop filter in the second generation of Audio Video coding Standard (AVS2) and High Efficiency Video Coding (HEVC) standard. Aiming at the problem that existing SAO algorithms had large amounts of computation and high complexity, an improved fast ratedistortion algorithm was proposed. In this new method, the original defined table of the offset values and its binary bit string to be written into the code stream were modified by analyzing the relationship between the different offset values of each class in the edge mode and its change of the ratedistortion, so that an early termination condition was set to quickly find the best offset value for the current SAO unit without calculating the ratedistortion cost of each offset. The experimental results show that, compared with the calculation results in AVS2, the proposed algorithm reduces not only the calculation amounts but also the number of cycles by 75% to find the best offset values and the operating time of inloop filter by 33%, which effectively lowers the complexity of the calculation in ensuring the ratedistortion of image barely changed.
Key words:the second generation of Audio Video coding Standard (AVS2); High Efficiency Video Coding (HEVC); Sample Adaptive Offset (SAO); offset values of edge mode; ratedistortion cost
0 引言
由于第二代数字音视频编解码标准(the second generation of Audio Video coding Standard, AVS2)和高效视频编码(High Efficiency Video Coding,HEVC)中采用的基于块的混合编码框架会带来块效应,即解码后的重构图像与原始图像存在差异[1-2], 因此,除了H.264/AVS原有的去块效应滤波(deblocking filter)外,HEVC/AVS2在编码过程中新加入了自适应样点补偿滤波(Sample Adaptive Offset,SAO)[3-4]。其中,自适应样点补偿在去块效应滤波之后进行[5],其主要作用是为了抑制编码中由变换量化等造成的振铃效应,从而进一步减少重构图像的失真。
本文将对自适应样点补偿滤波算法进行详细分析,在AVS2的标准下, 总结原边缘模式下的率失真算法中补偿值与对应码率代价之间的关系,在几乎不影响图像率失真代价的情况下,对原本定义的补偿值与写入码流的二元符号串之间的对应表稍作修改,并总结规律从而找到一种新的快速率失真算法,有效地降低了计算边缘模式下最优率失真代价的复杂度。
1 自适应样点补偿算法分析
1.1 SAO滤波设计
样值偏移补偿作为环路滤波的一部分,由于其主要目的也是为了减少原始图像与重构图像之间的误差,因此,SAO的关键思想是降低每个SAO单元的平均样本损失。其中SAO单元是由最大编码单元(Largest Coding Unit,LCU)导出,每个最大编码单元的SAO参数被写入条带数据中。为了能更大程度减少SAO参数的比特数,还引入合并模式来标记当前最大编码单元的SAO参数是否与它的相邻块相同。当该SAO单元选择合并模式时,当前块的SAO参数不是从码流中传入的,而是可以从它的相邻块中直接得到的。
在进行样值偏移补偿时,首先把一帧图像分为若干个LCU,把每个LCU作为一个SAO单元进行处理,通过计算各个模式下的率失真代价,选择最优的模式为该LCU的滤波类型[6]。SAO总共分为三种不同的模式:不补偿(OFF)、合并模式(Merge)和新补偿模式(New)。其中合并模式可分为上合并和左合并,新补偿模式又分为边缘补偿模式(Edge Offset,EO)和区间补偿模式(Band Offset,BO)。
1.2 样本补偿处理
为了减少重构图像与原始图像的差,需要对每个LCU进行样本补偿处理。其原理是把每个SAO单元中的样本根据不同模式分为不同的多个类,并为每个类获得一个补偿(offset)的值,然后把属于这个类中的所有样本值都加上该offset值。该SAO单元的模式索引以及每个类的offset值会编写进码流。
1)边缘补偿模式。
为了保持复杂度与编码效率之间的平衡,这里把边缘模式再分为4种不同的方向:水平、垂直、135°对角线和45°对角线,如图1所示。图中c表示当前样点,a和b表示相邻样点。根据所给的方向,每个采样点又可分为5类,其分类条件及每个类所对应的补偿值的取值范围如表1所示[7]。把当前LCU中的每个样本值与其相邻的两个样本值作比较得到其所属的类,并加上对应的offset值,其中第0类不需要进行补偿操作。
从表1可看出,由于第1类和第2类对应的样点值小于等于相邻点的样本值,因此采用的补偿值大多属于正数范围,第3和第4类则相反。对于每个类,在编码时需要计算得到最优的率失真所对应的offset的值,然后写入码流传到解码端。
2)区间补偿模式。
在每个LCU中,对同一区间的所有像素对应的样本值采用同一补偿值。如果每个采样点的样本值在0到255之间,则把整个样本值划分为32个区间,每个区间的宽度为8,并对应不同的offset值[8],每个offset的值在编码端通过计算率失真代价获得。在AVS2标准中,每个LCU只选择4个补偿值较大的区间进行补偿,其中两两相连, 因此当选择区间模式时,只需把两个区间的起始位置及对应的4个offset的值(取值范围为[-7, 7])传到解码端。
1.3 率失真代价计算
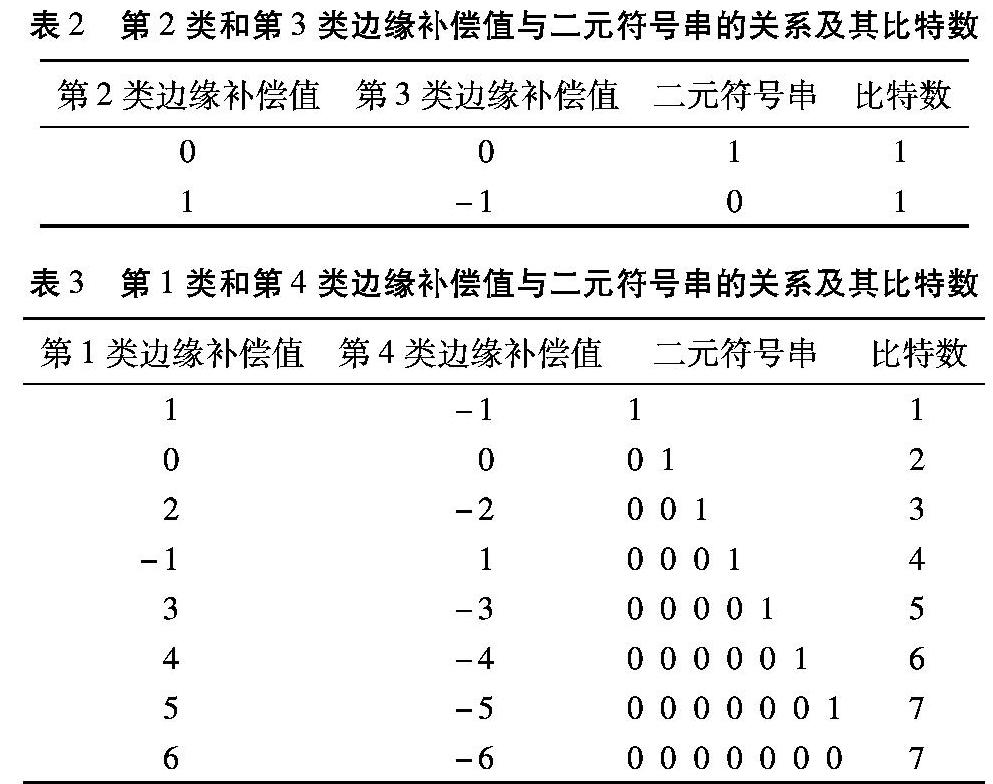
从以上对每个不同模式下的补偿操作的分析可以看出,无论是边缘模式还是区间模式都需要为每个类选择一个对应的offset的值。在AVS2中,是通过一种快速率失真算法,估算出范围内每个offset所对应的率失真代价,并选择最小的为该类的补偿值。这里使用的比特数并不是把offset的值真正写入码流而获得的,因此可以省去算数编码的时间,其offset值与估计的比特数如表2和表3所示[9]。这种算法的优点在于能比较精确地估计出最优的率失真代价所对应的补偿值,然而,图像由多个LCU组成,每个LCU需要分为亮度和色度三个分量分别计算,每个分量对应4种不同的边缘模式,而每种边缘模式又分为5类(其中有4类需要计算offset),这4类offset的值总共有18个,如果一一计算其对应的率失真代价,需要循环次数较多,而且由于原本定义的补偿值与比特率之间的对应关系没有规律,所以在计算码率代价时还需通过查表获得,增加了计算量和计算的复杂度。
2 改进的快速率失真算法
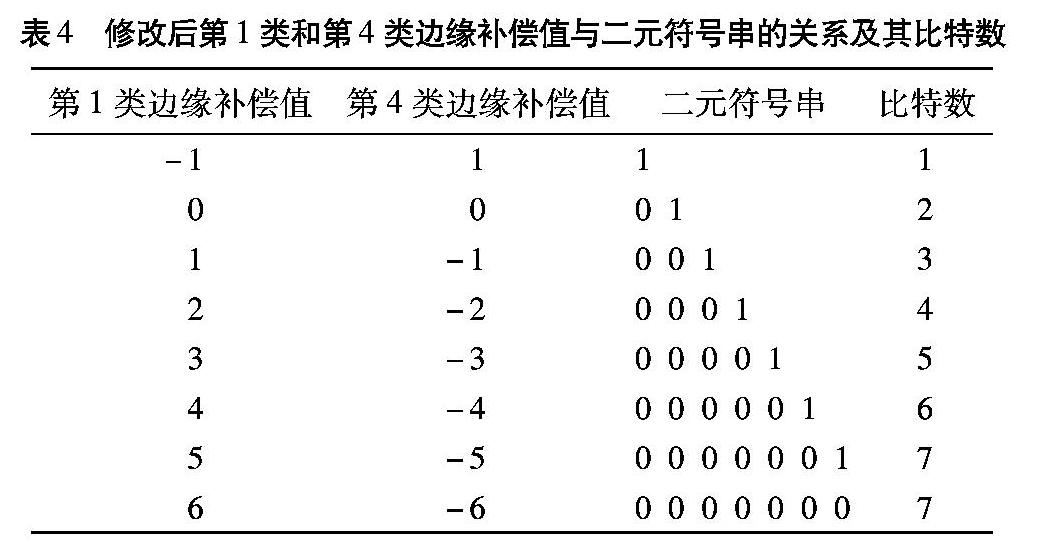
本文对计算率失真代价的公式进行分析,在上述快速率失真算法的基础上进一步改进,并且为了统一offset值的变化与比特数变化的对应关系,修改原本定义的第1和第4类边缘补偿offset值与写入码流的二元符号串之间的对应表,修改后如表4所示。在初步算得一个offset值以后,不需要一一计算率失真代价的公式,只需通过计算offset值的变化引起的图像质量的损失和码率代价之间的大小关系,得到一个提前终止的条件,从而减少了循环的次数和计算率失真代价的时间,有效地降低了计算的复杂度。
2.1.2 特殊情况分析
观察表4,同样以第1类边缘补偿模式为例,可以看出,当计算得到的最初offset值为6时,其比特率的变化并不满足offset为-1~5时的变化规律,因此需要分开进行讨论。由于当offset的值为-1~5时,仍然满足变化规律,这里只需将用上述快速率失真算法在-1~5时选出的最优offset值与offset=6时的率失真代价进行比较,得到一个较优的offset值作为该模式下的最终补偿值。另外,把表中offset=6和offset=5的情况进行比较,可以容易得出,当算得的最初offset值为6时,其率失真代价必定优于offset=5。
2.2 算法流程
首先,把当前最大编码块各个模式下统计得到的N和E代入式(2)。然后,把该值四舍五入到整数并归到表1中的不同类的取值范围内计算得到z,如果N等于0,则z等于0,令初始offset=z。最后,根据不同的类,循环算得最优的offset值,其具体过程如图2所示。
1)第2类和第3类。由表2可以看出,这两类不同的offset值所对应的码率代价是相同的,即g([x])相同,因此,无需循环计算,初始的offset值即为最优值。
2)第1类。若z=-1,则无需循环,直接得到最终的offset=-1。若z=6,见2.1.2节;否则,让补偿值x从z到-1范围内循环。判断式(3)是否成立:若成立,则提前终止循环,得到最优的offset=x;否则得到最终offset=-1。
3)第4类。若z=1,则无需循环,直接得到最终的offset=1。若z=-6,见2.1.2节;否则,让补偿值x从z到1范围内循环。判断式(4)是否成立:若成立,则提前终止循环,得到最优的offset=x;否则得到最终offset=1。
3 实验结果与分析
3.1 实验平台与参数配置
本文基于AVS2P2的参考软件RD11.1,所使用的开发环境为VS 2013。实验所用平台配置为:Intel Celeron CPU N2920 1.86GHz,内存为4GB,操作系统为Windows 8.1。本次实验中采用了4种不同分辨率的视频序列来测试改进算法的性能,每个视频序列的分辨率与配置参数如表5所示。
3.2 实验结果与性能分析
表6是4种不同分辨率的测试序列在RA(Random Access)编码模式下,打开SAO并且关闭自适应环路滤波(Adaptive Loop Filter,ALF)的情况下获得的码率和PSNR的对比。从表中数据可以看出,改进的算法相比原算法,在图像亮度分量(ΔPSNR_Y)的质量上平均有0.01的损失,在色度分量U(ΔPSNR_U)和V(ΔPSNR_V)的质量上分别有0.02和0.01的损失,在码率上有0.77%的增益。这是由于本算法改变了某些offset值与写入码流的二元符号串之间的对应关系,但从实验结果看,对整体的编码性能造成的影响可忽略不计。
表7为上述实验条件下统计的原算法与改进后算法在边缘模式下计算补偿值的循环次数比较,从实验数据中可以看出,无论对于多少分辨率的视频序列,改进后的算法比原算法的循环次数平均减少了75.4%,且就环路滤波的运行时间平均减少了约33%。不仅如此,原算法需要把当前offset值带入式(1)(二阶)并且查表2和表3获得对应的比特率,从而计算得到率失真代价。而本文算法除了2.1.2节的特殊情况外,大部分的值只需通过循环计算判断式(3)和(4)(一阶)就可得到最优的offset值,大大降低了计算的复杂度,提高了编码器的效率。
4 结语
本文在分析AVS2视频编码标准中自适应样点补偿的快速率失真算法的基础上,在初步得到一个补偿值后,通过比较offset值的变化引起的图像质量的损失和码率代价之间的大小关系,得到一个提前终止的条件,并在不需要计算每个offset值的率失真代价的同时获得该模式下最优的补偿值。实验表明,改进后的率失真算法大大减少了循环的次数和计算率失真代价的时间,在几乎不影响图像率失真性能的同时有效地降低了计算的复杂度,有利于本算法的实时应用。
参考文献:
[1]HE Z, YU L, ZHENG X, et al. Framework of AVS2video coding[C]// Proceedings of the 2013 20th IEEE International Conference on Image Processing. Piscataway, NJ: IEEE, 2013: 1515-1519.
[2]蔡晓霞, 崔岩松, 邓中亮, 等. 下一代视频编码标准关键技术[J].电视技术, 2012, 36(2):80-84.(CAI X X, CUI Y S, DENG Z L, et al. Model of nextgeneration video standard and relative key technologies [J]. Video Engineering, 2012, 36(2):80-84.)
[3]黄铁军, 高文, 王国中.数字音视频编解码技术标准AVS发展历程与应用前景[J].上海大学学报(自然科学版), 2013, 19(3): 221-224.(HUANG T J, GAO W, WANG G Z. Development history and application prospect of AVS digital audio and video coding and decoding standard [J]. Journal of Shanghai University(Natural Science Edition), 2013, 19(3): 221-224.)
[4]马思伟.AVS视频编码标准技术回顾及最新进展[J].计算机研究与发展, 2015, 52(1):27-37.(MA S W. History and recent developments of AVS video coding standards[J]. Journal of computer Research and Development, 2015, 52(1): 27-37.)
[5]NORKIN A, BJNTEGAARD G, FULDSETH A. HEVC deblocking filter[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2012, 22(12):1746-1754.
[6]FU CM, ALSHINA E, ALSHIN A, et al. Sample adaptive offset in the HEVC standard[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2012, 22(12):1755-1763.
[7]PIAO Y, LEE S, KIM C, et al. Sample adaptive offset for AVS2[C]// Proceedings of the 46th AVS Conference. [S.l.]: Samsung Electronics, 2013: 2-3.
[8]MAANI E, NAKAGAMI O. Flexible band offset mode in SAO: JCTVCH0406[R]. San Jose, CA: Joint Collaborative Team on Video Coding, 2012: 1-10.
[9]AVS工作组.GB/T信息技术高效多媒体编码第2部分:视频(征求意见稿)[S]. 北京:全国信息技术标准化技术委员会(SAC/TC 28), 2015.(Work group of audio video coding standard. Information technology — advanced media coding, part 2: video [S]. Beijing: China National Information Technology Standardizaton Network (SAC/TC 28), 2015.)
[10]唐华敏, 杜建超, 王庆雷. 视频编码标准HEVC中的环路滤波技术分析[J].电视技术, 2014, 38(11):1-4.(TANG H M, DU J C, WANG Q L. Analysis of inloop filter technique in video coding standard HEVC [J]. Video Engineering, 2014, 38(11):1-4.)
[11]MINEZAWA A, SUGIMOTO K, SEKIGUCHI S. Improved edge offset coding for SAO: JCTVCI0066[R]. Geneva, CH: Joint Collaborative Team on Video Coding, 2012.
[12]FU C M, CHEN C Y, HUANG Y W. Sample adaptive offset for HEVC[C]// Proceedings of the 2011 IEEE 13th International Workshop on Multimedia Signal Processing. Piscataway, NJ: IEEE, 2011: 1-5.
