基于加权一个变量的一阶灰色模型的动态轨迹预测算法

江艺羡 张岐山

摘要：针对基于Kalman滤波的跟踪方法需要对噪声特性和轨迹的运动规律进行假设的不足，将新陈代谢一个变量的一阶灰色模型（GM（1，1））引入动态轨迹预测方法，提出一种基于加权灰色GM（1，1）模型的动态轨迹预测算法（TR_GM_PR算法）。首先，顺序截取预测点前不同长度的子轨迹，计算采用灰色GM（1，1）模型拟合各子轨迹的相对误差及相应的预测值；其次，对各子轨迹的相对拟合误差进行归一化处理，根据处理后的结果设置各子轨迹预测值权重；最后，将各子轨迹获得的预测值与其对应权重的线性组合作为轨迹未来运行趋势的最终预测结果。采用2000— 2008年美国大西洋飓风数据进行实验，TR_GM_PR算法6h的预测正确率为67.6056%，比基于模式匹配的飓风预测方法提高2.6056个百分点。实验结果表明， TR_GM_PR算法适用于轨迹短期预测。此外，该预测算法计算简单、实时性高，能够有效提高动态轨迹的预测正确率。

关键词：一个变量的一阶灰色模型；新陈代谢；轨迹；预测

中图分类号：TP941.5 文献标志码：A

Abstract：The noise assumption and motion assumption of trajectory should be demanded in dynamic trajectory prediction based on Kalman filter. In order to eliminate this insufficiency， the metabolism GM（1，1） model was introduced in dynamic trajectory prediction. Thus a prediction algorithm based on weighted grey GM（1，1） model （TR_GM_PR algorithm）was presented. Firstly， subtrajectories with different length before forecasting point were cut out in order， then the relative fitting errors and predicted values of subtrajectories were calculated using grey GM（1，1） model. Secondly， the normalization processing of relative fitting errors was carried out， and the weights of predicted values were set according to the result. Finally， using the linear combination of predicted values and their corresponding weights， the running tendency of trajectory in future was predicted. Experiments were conducted with the Atlantic weather Hurricane data from 2000 to 2008. Compared with hurricane trajectory prediction method with pattern matching， TR_GM_PR algorithm improves the prediction accuracy ratio of 6 hours by 2.6056 percentage points to 67.6056%. The experimental results show that TR_GM_PR algorithm is suitable for shortterm trajectory prediction. In addition， the new algorithm has simple calculation and high realtime performance， and can effectively improve the prediction accuracy of dynamic trajectory.

Key words：Grey Model（1，1） （GM（1，1））； metabolism； trajectory； prediction

0 引言

随着科学技术的发展，移动轨迹预测已成为许多研究领域的热门课题[1-4]。利用移动对象轨迹发现有价值的信息，实现对移动对象未来的准确预测是人们关注的重点。轨迹预测方法常见的有基于马尔可夫模型的位置预测、基于频繁路径的位置预测、基于线性回归模型的预测和基于Kalman滤波的跟踪预测等[5]。这些方法在轨迹预测方面具有自己的优势，但从总体看，这些预测方法还存在一些问题，前两种方法运算量大，实时性较差；后两种方法实时性较好，但两者大多需要假设轨迹作匀速或匀加速直线运动，该假设往往不符合实际情况，跟踪误差比较大，难以对运动目标下一步的运动轨迹进行分析[6]。此外，Kalman滤波存在初值选取、噪声参数选择以及可能发散等问题[7]。而基于灰色理论模型的预测方法同样也占有一定的地位[8]。基于包含一个变量的一阶灰色模型（Grey Model（1，1），GM（1，1））的轨迹预测思想并不复杂，对缺少基础资料的预测能够得到较好的预测效果，与别的预测方法相比，它用到的样本数据较少，不需要对随机噪声和目标运动规律作出假设，而且预测结果的准确度也较为理想，能够实现快速、有效的短期预测，因此在预测领域中占有一定的地位[9-10]。因此，本文利用加权的方式，对新陈代谢灰色GM（1，1）模型进行改进，并将其应用于飓风轨迹的预测研究。

2 改进算法描述

根据灰色新息理论，当一个最新数据加入原始数列时，当前序列反映系统的最新信息，但系统随着量变的积累可能会发生质的突变，因此需要舍弃旧数据。等维新息新陈代谢灰色GM（1，1）模型为满足以上需求而建立，并在应用中得到理想效果。但维数的确定没有明确的方法：若维数太少，无法充分表达序列蕴含的信息；若维数太大，截取的数据列可能包含突变点。为解决该问题，本文提出基于加权灰色GM（1，1）模型动态轨迹预测方法。该方法利用轨迹不同长度子轨迹的相对拟合误差设置权重，以加权方式对轨迹未来趋势进行预测。

在预测过程中，长度较小的子轨迹拟合的平均相对误差较小，但拟合的曲线变化相对较陡峭；长度较大的子轨迹拟合的平均相对误差较大，但曲线相对比较平缓，因此以加权的方式可以保证预测的准确性。

3 算例分析

本文进行三个实验。算例1同具有N个变量的多变量灰色MGM（1，N）模型（Multivariable Grey Model（1，N）， MGM（1，N））相比较；算例2同等维新息灰色GM（1，1）模型相比较；算例3根据飓风预测准确性将本文算法同其他轨迹预测方法相比较。本文所提基于加权灰色GM（1，1）模型的动态轨迹预测算法（Prediction Algorithm of Dynamic Trajectory based on Weighted Grey GM（1，1） Model， TR_GM_PR algorithm）的实验结果如下。

算例1 TR_GM_PR算法在无人机飞行轨迹数据中的实验。

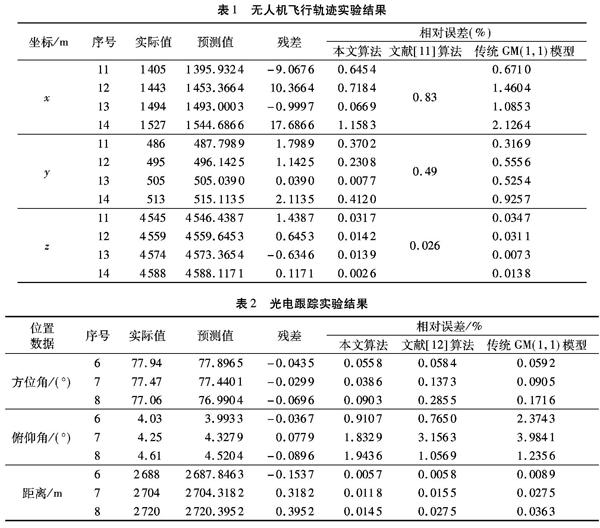
采用无人机飞行轨迹的位置坐标数据为实验数据[11]。前10个数据预测第11个数据，前11个数据预测第12个数据，以此类推。表中同时列出灰色GM（1，1）模型利用预测点前所有数据进行拟合获得预测值的相对误差。实验结果见表1。文献[11]第11个数据的预测坐标为（1393.3，488.4，4546.2），各坐标相对误差分别为0.83%，0.49%和0.026%，三者整体平均相对误差为0.4491%。本文算法获得的预测值坐标为（1395.9324，487.7989，4546.4387），相对误差分别为0.6454%，0.3702%与0.0317%，三者整体平均相对预测误差为0.3485%。传统GM（1，1）模型在第11个数据的预测坐标相对误差分别为0.6710%，0.3169%和0.0347%，三者整体平均相对误差为0.3409%。采用传统GM（1，1）模型在第11个位置的预测效果较好。从第11个数据至第14个数据的预测效果分析，本文算法的平均相对误差分别为0.3491%，0.3211%，0.0295%和0.5243%；而采用传统GM（1，1）模型的平均相对误差分别为0.3409%，0.6823%，0.5393%和1.0220%。显然本文算法的整体预测效果最理想。因此合理确定不同长度子轨迹对预测值的影响很有必要。

算例2 TR_GM_PR算法在光电跟踪数据中的实验。

实验采用文献[12]的光电跟踪数据。实验利用前5个数据预测第6个数据，前6个数据预测第7个数据，以此类推。模型预测结果见表2。文献[12]采用等维新息优化灰色GM（1，1）模型，模型预测精度较理想。采用灰色GM（1，1）模型对预测点前整个轨迹进行拟合，得到的预测值相对误差见表2最后一列。采用传统方法获得的预测效果有些优于文献[12]。从而说明，新陈代谢GM（1，1）模型维数的确定影响模型预测精度。而本文模型精度整体优于文献[12]与传统方法。

算例3 TR_GM_PR算法在飓风轨迹数据中的实验。

实验选取2015年1月至5月美国大西洋飓风轨迹数据（http：//weather.unisys.com/ hurricane/ atlantic/ index.html），数据列间隔时间为6h，若预测6h后的轨迹位置，则取最后1个数据为预测点，预测点前轨迹作为拟合数据。若预测12h后的轨迹位置，则取最后1个数据为预测点，最后2个数据除外的剩余轨迹作为拟合数据。以此类推。

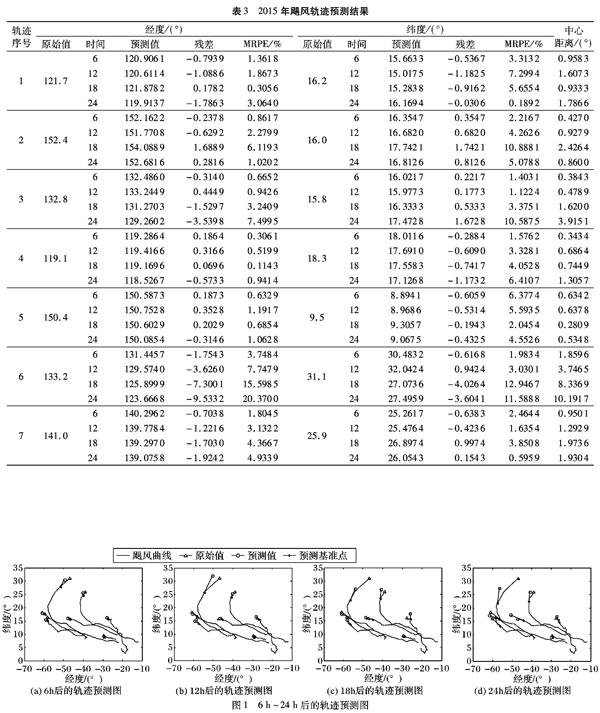
预测结果见图1，图中经度-70°表示西经70°。轨迹6h后的运行方向与原始轨迹相差较小。轨迹24h后的运行方向与原始数据相差较大。主要原因是灰色GM（1，1）模型为指数曲线的单调性使得模型对于呈现U型或S型的原始曲线拟合效果较差。受飓风气压、风力等因素的影响，预测的间隔时间越长，飓风轨迹运行方向越会出现突变点，因此基于加权灰色GM（1，1）模型的预测方法适合于短期轨迹预测。

为更详细分析本文算法在飓风轨迹的预测结果，以表格的形式列出2015年7条轨迹经度与纬度的预测值，结果见表3。表中列出每条轨迹对应的经度与纬度在6～24h后的预测值，以及预测值与实际值的残差与平均相对百分比误差。由表3可以看出，第4号与第5号飓风的预测平均相对误差较小，第6号轨迹的预测偏差较大。整体而言，随着预测时间变长，预测值与实际值的残差变大。借鉴文献[5]对飓风中心点预测准确性的规定：若实际轨迹与预测轨迹中心点间的距离不超过1°，则表示轨迹预测正确。从表3最后一列可看出，飓风在短期的轨迹预测正确数较多，预测时间变长后，预测正确的轨迹数变少。

为减少小样本对轨迹预测正确率的影响。采用2000—2008年的飓风数据作为预测检验样本。通过实验， 6h的轨迹预测准确性为67.6056%，12h降为36.2205%。18h为28.5714%，24h为22.3529%，见图2。文献[5]采用模式匹配历史数据对轨迹进行预测，匹配正确轨迹的预测准确率为65%。因此，基于加权灰色GM（1，1）模型的轨迹预测方法针对短期的轨迹预测具有较高的准确性，预测效果较好。而模型对中长期的轨迹预测效果不甚理想。

4 结语

等维新息模型的维数影响模型预测精度，为提高灰色GM（1，1）模型预测精度，本文以加权的方式建立不同维新息灰色GM（1，1）模型。权重的设置依据不同长度子轨迹拟合的平均相对误差：平均相对误差大的权值较小，反之权值较大。实验结果表明，对于单调性的轨迹，本文灰色GM（1，1）模型在轨迹预测方面取得较好的效果。

对于类似U型或S型曲线的轨迹，灰色GM（1，1）模型拟合结果较不理想。飓风实例中，本文模型在轨迹短期预测准确性达到67.6056%，预测效果理想。本文基于加权灰色GM（1，1）模型的轨迹预测算法仅以轨迹的位置点为基础，计算方法简单，短期预测效果较好，但不适于中长期实时预测。

参考文献：

[1]KAYACAN E， ULUTAS B， KAYNAK O. Grey system theorybased models in time series prediction[J]. Expert Systems with Applications， 2010， 37（2）： 1784-1789.

[2]LEI M L， FENG Z R. A proposed grey model for shortterm electricity price forecasting in competitive power markets[J]. International Journal of Electrical Power and Energy Systems， 2012， 43（1）： 531-538.

[3]YIN M S， TANG H W V. on the fit and forecasting performance of grey prediction models for Chinas labor formation[J]. Mathematical and Computer Modelling， 2013， 57（3）： 357-365.

[4]TABASZEWSKI M， CEMPEL C. Using a set of GM（1， 1） models to predict values of diagnostic symptoms[J]. Mechanical Systems and Signal Processing， 2015， 52【【查到的卷就是这样52 5353： 416-425.

[5]董鑫， 皮德常.基于模式匹配的飓风轨迹预测方法[J]. 小型微型计算机系统， 2014， 35（5）：983-988.（DONG X， PI D C. Hurricane trajectory prediction method with pattern matching[J]. Journal of Chinese Computer Systems， 2014， 35（5）： 983-988.）

[6]袁基炜， 史忠科.一种基于灰色预测模型GM（1， 1）的运动车辆跟踪方法[J].控制与决策， 2006， 21（3）：300-304.（YUAN J W， SHI Z K. A method of vehicle tracking based on GM（1， 1）[J]. Control and Decision， 2006， 21（3）：300-304.）

[7]HUH K， PARK J， HWANG J， et al. Stereo visionbased obstacle detection system in vehicles[J]. Optics and Lasers in Engineering， 2008， 46（2）： 168-178.

[8]刘思峰， 党耀国， 方志耕， 等.灰色系统理论及其应用[M].5版.北京：科学出版社， 2010： 146-152.（LIU S F， DANG Y G， FANG Z G， et al. Grey System Theory and Its Application[M].5th ed. Beijing： Science Press， 2010： 146-152.）

[9]陶剑锋， 陈伏虎.基于GM（1， 1）模型的机动目标跟踪方法研究[J].系统工程与电子技术， 2009， 32（6）：1396-1399. （TAO J F， CHEN F H. Maneuvering target tracking based on GM（1， 1）[J]. Systems Engineering and Electronics， 2009， 32（6）： 1396-1399.）

[10]杨炜， 魏朗， 刘永涛， 等.改进GM（1， 1）模型的前车检测与跟踪研究[J].计算机工程与设计， 2012， 33（11）： 4278-4282. （YANG W， WEI L， LIU Y T， et al. Research on detection and tracking of front vehicle based on modified GM（1， 1） model[J]. Computer Engineering and Design， 2012， 33（11）： 4278-4282.）

[11]柯宏发， 何可， 陈永光.运动目标的MGM_1_N轨迹预测算法[J].武汉大学学报（信息科学版）， 2012， 37（6）：662-666. （KE H F， HE K， CHEN Y G. Trajectory prediction algorithm of moving object based on MGM（1， N）[J]. Geomatics and Information Science of Wuhan University， 2012， 33（11）： 4278-4282.）

[12]王朝曦， 吴学铜， 黎凡.灰色预测优化模型及其在光电跟踪中的应用[J].光学与光电技术， 2015， 13（1）：55-59. （WANG Z X， WU X T， LI F. Grey prediction optimized model and application in opticalelectric tracking[J]. Optics and Optoelectronic Technology， 2015， 13（1）： 55-59.）