基于空间邻近的点目标聚类方法

余莉 甘淑 袁希平 李佳田

摘要：空间聚类是空间数据挖掘和知识发现领域的主要研究方向之一，但点目标空间分布密度的不均匀、分布形状的多样化，以及“多桥”链接问题的存在，使得基于距离和密度的聚类算法不能高效且有效地识别聚集性高的点目标。提出了基于空间邻近的点目标聚类方法，通过Voronoi建模识别点目标间的空间邻近关系，并以Voronoi势力范围来定义相似度准则，最终构建树结构以实现点目标的聚集模式识别。实验将所提算法与Kmeans、具有噪声的基于密度的聚类（DBSCAN）算法进行比较分析，结果表明算法能够发现密度不均且任意形状分布的点目标集群，同时准确划分“桥”链接的簇，适用于空间点目标异质分布下的聚集模式识别。

关键词：空间聚类；Voronoi图；空间邻近；桥链接

中图分类号：TP181 文献标志码：A

Abstract： Spatial clustering is one of the vital research directions in spatial data mining and knowledge discovery. However， constrained by the complex distribution of uneven density， various shapes and multibridge connection of points， most clustering algorithms based on distance or density cannot identify high aggregative point sets efficiently and effectively. A point clustering method based on spatial proximity was proposed. According to the structure of point Voronoi diagram， adjacent relationships among points were recognized.

The similarity criteria was defined by region of Voronoi， a tree structure was built to recognize pointtarget clusters. The comparison experiments were conducted on the proposed algorithm， Kmeans algorithm and DensityBased Spatial Clustering of Applications with Noise （DBSCAN） algorithm. Results show that the proposed algorithm is capable for identifying clusters in arbitrary shapes， with different densities and connected only at bridges or chains， meanwhile also suitable for aggregative pattern recognition in heterogeneous space.

Key words：spatial clustering； Voronoi diagram； spatial proximity； bridge connection

0 引言

点目标是二维矢量空间中以坐标形式精确表达一系列事件或现象位置分布的几何要素，其聚类分析采用指定的相似性测度计算目标间位置的接近程度，进而以数学建模发现空间事物聚集分布的感兴趣模式，广泛应用于图形图像学、地图学、气象学、环境控制、公共卫生与服务等自然、社会及经济领域。

现有的六类点目标聚类研究[1]主要以距离和密度判断目标位置的聚集性：

1）距离。以欧氏距离计算点间距离，常用于划分、层次、模型、图论聚类。划分聚类通过定义和迭代优化距离准则函数来实现目标的划分[2-5]。层次聚类根据点间距离排序，分别采用“从下至上”和“从上之下”两种策略对点目标进行融合或划分[6-9]。模型聚类中，模拟昆虫社交行为和能力的群聚类算法[10-14]采用随机搜索距离增量优化聚类结果，直至满足终止条件；模拟神经元对信息的吸收、处理、反馈等能力的自适应共振网络（Adaptive Resonance Theory 2， ART2）[15]、自组织映射网络（SelfOrganizing Maps， SOM）[16]及改进算法TreeART2[17]、动态增长自组织映射模型GSOM（Growing SelfOrganizing Map）[18]和TGSOM（Treestructured Growing SelfOrganizing Map）[19]以距离计算输入模式向量的相似性，并设置相似度阈值判断获胜神经元；模拟空间数据场间凝聚力相互作用的场聚类[20-23]以距离构建场强函数计算目标间凝聚力。图论聚类的典型算法是采用Delaunay三角网剖分点，并以距离计算三角网边长，进而定义边长约束逐层删除无效三角形边来发现簇类[24-26]。然而，距离相似度仅表征点对点的相似信息，缺乏多点或局部区域目标的聚集特征的判断，算法需要设置收敛条件并对聚类结果进行迭代优化，不仅计算量大，且收敛条件难以自动定义，同时聚类质量受簇的形状和异常值影响较大[3]，图论聚类中三角网以短边表达“桥”链接的点目标，与集群目标间连接的三角形短边难以区分[24]。

2）密度。通过计算指定范围内点目标的分布密度判断聚集程度，常用于密度和网格聚类。密度聚类通过定义搜索区域或区域半径以及区域内包含目标的最小数量来判断密度连通性以融合点簇[27-29]。网格聚类采用规则格网划分点目标，以格网的4邻域或8邻域判断目标邻近关系，并设置格网内目标密度阈值以合并包含了高密度目标的格网[30-31]。密度是区域内点目标聚集性的整体表征，此类算法能够识别变密度和不规则形状的簇，但是密度的计算依赖于用户对区域半径、密度阈值、格网尺度等核心参数的设置，聚类质量对先验知识的高需求限制了算法在大空间数据集的应用。

为了在用户输入领域知识最小化的基础上识别密度不均和任意形态的点簇，本文提出了基于空间邻近的点目标聚类方法——PCVD（Points Clustering using Voronoi Diagram），鉴于Voronoi结构在捕捉空间离散点间邻近关系的优势[32]，本文以点目标Voronoi图的一阶邻近特性及势力范围面积共同定义点目标及其邻近目标的聚集性强度的判断准则，并选择平均统计量自动计算强度阈值，构建树结构实现类内目标、类边界目标、离群目标的划分。实验部分采用模拟数据集对PCVD、Kmeans和具有噪声的基于密度的聚类（DensityBased Spatial Clustering of Applications with Noise， DBSCAN）算法进行对比分析，并于结论中对PCVD算法的适用性和伸缩性进行论述。

1 聚集性判断条件

点目标聚集模式的形成是空间异质性特征的表现，当点目标之间存在相互吸引或相互关联的空间相互作用时，目标的空间位置分布才会出现有意义的簇[32]。空间目标位置分布的聚集性判断条件可分为两方面：1）准确判断目标间的拓扑邻近关系，以确认目标间不存在其他任意阻碍二者可视性或连通性的目标；2）能够精确评估邻近目标间的真实距离。

1.1 一阶邻近关系

二维空间内的Voronoi图互不重合且连续铺盖，将所有空间目标联系在一起，隐含地表达力了目标的侧向邻近信息（lateral adjacency information）[33]。陈军等提出V9I（Voronoiregion based 9 Intersection）模型，定义了两个空间目标的Voronoi势力范围（Influence Region， IR）[33]共边时属于空间邻近关系。

1.2 真实距离测算

由点目标Voronoi图几何特性可知，随着点目标的不均匀分布，其Voronoi图的势力范围亦发生变化，以Voronoi面积定量化，则具体表现为：点目标生长元分布密集的区域，生成的Voronoi面积相对较小；反之，分布稀疏的区域，生成的Voronoi面积相对较大。图1的近圆形簇采用从内向外，从密集到疏松分布的点目标作为生长元生成点目标Voronoi图，当空间点目标分布密集时，得到的Voronoi图面积相对较小，反之，当空间点目标分布稀疏时，得到的Voronoi图面积相对较大。由此可得，点目标Voronoi面积是表征点目标聚集程度的指标之一。

但从图1所含两个聚集性点群及其Voronoi图细节显示，每个簇的类内目标的Voronoi图面积是随聚集性的增强而减小，可通过判断Voronoi面积值来识别类内目标；而类边界目标的Voronoi面积却是相对较大的，且根据边界点的分布差异，其Voronoi面积值呈随机分布，无法直接识别。据观察，类边界目标的一阶邻近目标中至少包含一个类内目标，且类边界目标与该类内目标存在高度聚集性，可识别为同类，因此，在相似度判别时可根据这一规律选择与边界目标最近的类内目标来识别类边界目标。

与常规计算点间距离不同，本文利用点目标生成的Voronoi图面积来评估单个点目标与其周围目标聚集性的强弱，定义如下：

3 树结构聚类

根据聚类准则，PCVD算法搜索同类点目标作为树节点以构建树结构，具体表现为：

1）遍历搜索所有空间点目标，若Q（pi）的值大于Σ，则选取点目标pi作为树结构的根节点；搜索目标pi的一阶Voronoi邻域内的其他目标，若搜索到的点目标pj满足准则1，则将目标pj作为pi节点的下一级子节点，但若搜索到的目标pj满足准则2，则将目标pj作为pi节点的下一级叶子节点；再根据准则1～3，依次对每个子节点的一阶Voronoi邻域内的其他目标进行逐层搜索判断，直至叶子节点为止；将该棵树结构中的所有节点进行标记，单树构建完成。

2）继续遍历空间目标，按照1）中的过程，从余下未被标记的空间点目标中选取根节点，并逐层搜索至单树中再无子节点产生。

3）直至遍历完所有空间点目标，则树结构构建结束。

树的数量即为聚类的个数，每棵树的根节点和子节点表示类内目标，叶子节点代表类边界目标，而未被标记的目标则属于离群目标。

在树结构的构建过程中，对于叶子节点的判断有“先到先得”的优势，即：当两个类C1和C2距离相对较接近时，依据准则2的判断，部分边界目标即是类C1的边界，又是类C2的边界，其归属取决于构建C1和C2的树结构的顺序，使得边界目标不一定分布在距离其较近的类中，而发生误判。PCVD算法在树结构构建完成后，对叶子节点的归属进行验证：

1）遍历树结构中的所有叶子节点；

2）对于单个叶子节点pi，搜索pi的一阶Voronoi邻近目标，比较每个邻近目标的与叶子节点pi的聚集性强弱，根据准则4，点目标pi与聚集性强度Q最大的目标属于同类。

叶子节点归属的检验是对类边界的修正，可提升聚类结果的准确性。

4 PCVD算法描述

5 实验与讨论

实验模拟了不同空间分布的点目标集合， 分别以距离计算相似度的Kmeans算法[2]、以密度计算相似度的DBSCAN算法[27]和以Voronoi结构计算聚集性强度的PCVD算法进行对比聚类，旨在对PCVD算法的有效性和稳定性进行验证。

5.1 模拟数据实验

1）密度分布不均的点目标。

图2（a）中以848个点模拟了密度分布不均，且高密度点集被稀疏点集包围的空间点目标分布。对比实验结果显示：图2（b）为聚类数目k=2的Kmeans算法结果；图2（c）为邻域包含最小目标数MinPts=5，邻域半径Eps=13时，DBSCAN算法的聚类结果；图2（d）为缩放因子C=6的PCVD算法结果，可以看出，Kmeans算法虽将点目标分为两类，但无法识别密度较为稀疏的离群目标，DBSCAN和PCVD算法能够识别变密度簇中的高密度目标，并准确分为两类，聚集目标的识别不因离群目标的存在而发生误判。

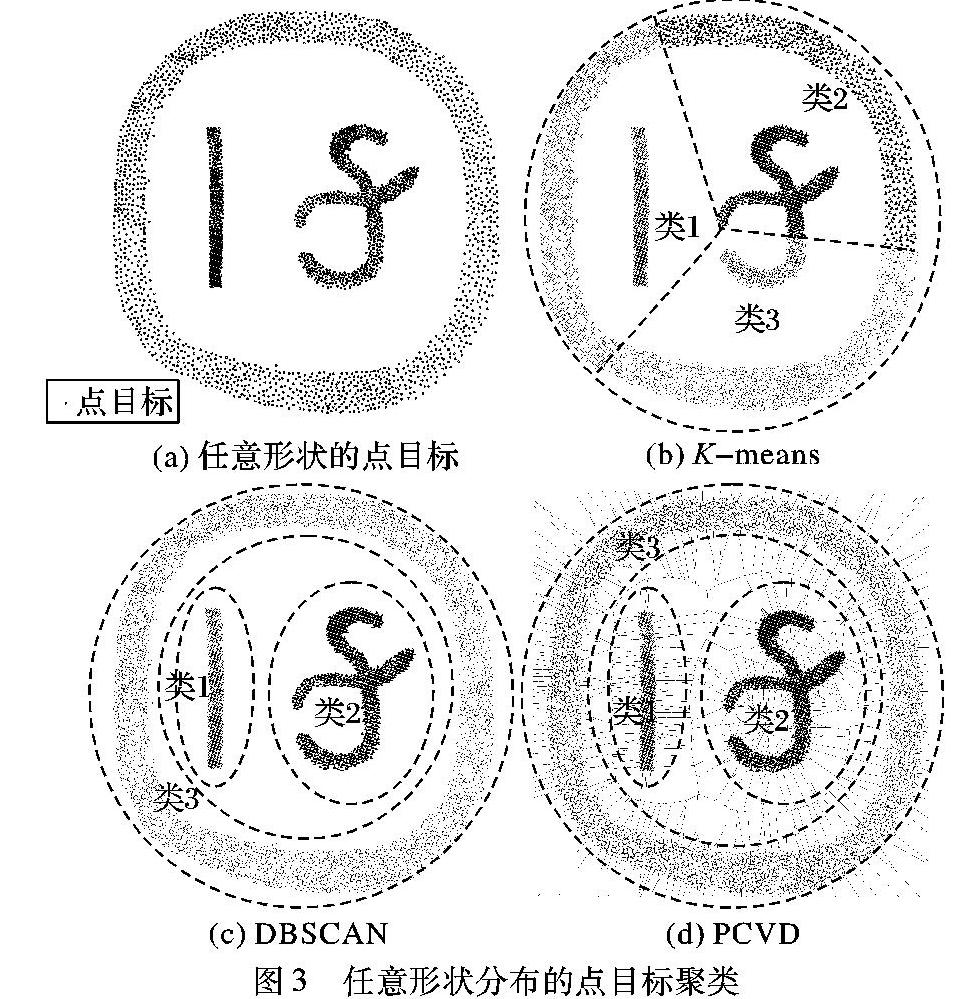
2）任意形状分布的点目标。

图3（a）中以2947个点模拟了任意形状分布的空间点目标簇，包含圆环、带状、不规则簇。对比实验结果显示：图3（b）为聚类数目k=3的Kmeans算法结果；图3（c）为MinPts=5， Eps=33时，DBSCAN算法的聚类结果；图3（d）为C=1的PCVD算法结果，可以看出，Kmeans算法受簇形状限制，不能准确划分点目标，DBSCAN和PCVD算法将点目标划分为三类，聚类结果不受簇形状的影响。

3）“桥”链接的点目标。

图4（a）中以1460个点模拟了存在多“桥”链接分布的空间点目标簇。对比实验结果显示：图4（b）为聚类数目k=2的Kmeans算法结果；图4（c）为MinPts=5， Eps=28时，DBSCAN算法的聚类结果；图4（d）为C=7的PCVD算法结果，可以看出，DBSCAN算法不能划分被“桥”链接的类，Kmeans和PCVD算法能够区分“桥”链接的簇。

综合对比实验，以距离计算点间相似度的方法适于识别圆形和近圆形簇，对离群点目标敏感，难以准确提取聚集度高的点集；以密度搜索聚类的方法能够识别密度不均和不规则形态的簇，但难以识别“桥”链接的簇，PCVD算法利用Voronoi图的邻近关系和面积共同判断目标聚集性，点目标Voronoi面积越小，聚集性越强，且“桥”目标的Voronoi图面积一般大于集群目标的Voronoi图面积，因此能准确识别模拟数据集中的簇，同时算法对离群点的处理较为稳健。

5.2 算法性能分析

1）PCVD算法的时间复杂度。

纵观PCVD算法聚类过程，若空间待聚类点目标数目为n，聚集性强度值的计算量与目标数量呈线性增加，该阶段算法的时间复杂度为O（n）；单一树结构构建的过程类似于二叉树构建的过程，建树阶段算法的时间复杂度为O（n log n）；类边界目标的检验亦与叶子节点的数量呈线性增加，最坏情况是所有点目标皆为叶子节点，则该阶段算法的时间复杂度为O（n），综合可得PCVD算法的时间复杂度为O（n log n）。

2）强度阈值的计算。

PCVD算法以平均值计算强度阈值，并以常数C的取值调节识别目标聚集性的强弱，C值越小，发现目标的聚集性越弱，类内包含的离群目标使得类内所有点目标的Voronoi面积平均值越大；反之，C值越大，发现目标的聚集性越强，使得类内所有点目标的Voronoi面积平均值越小。采用5.1节中模拟的三个数据集并顺序编号，将常数C取值从1至10，分别计算每个数据集中类1包含的所有点目标的Voronoi面积平均值，绘制类内目标对应的Voronoi面积平均值随不同常数C取值而变化的折线图，如图5所示。

由图可知，当空间目标簇之间的分布密度近似时，如数据集2，常数C的改变对类内目标的Voronoi面积平均值影响微弱，PCVD算法以聚集性强度的均值（C=1）作为阈值，能够满足点目标聚集模式的识别，算法无需自定义参数，如图3（d）；而当空间目标簇之间的分布密度差异较大或存在空间离群点时，如数据集1和数据集3，稀疏分布目标的聚集性强度值远远小于聚集性高的目标的聚集性强度，强度阈值（平均值）因受到离群目标聚集性强度值的影响而偏小，聚类时，需要适当地调整常数C以增加强度阈值，才能够发现聚集性高的目标。图5中，数据集1在C=6后，C值的取值对类内目标的Voronoi面积平均值变化影响不大，算法在该处得到合适的聚类结果，同样，数据集3在C=7后亦使类内目标的Voronoi面积平均值趋于稳定。因此，当常数C由小到大变化过程中，当类内目标的Voronoi面积平均值趋于稳定时，算法能够发现聚集程度高的点目标簇。

6 结语

PCVD聚类算法的构建有利于点目标位置分布的结构、相互关系、隐含特征等感兴趣模式的识别，基于Voronoi图无缝的空间邻近关系表达来判断离散点目标间的可视性，并以聚集性强度来定量计算点目标与周围目标的聚集性，最终构建树结构搜索集群目标聚类，并对类边界目标进行优化。模拟数据实验证明，PCVD算法能够识别密度不均、簇形状任意分布和“桥”链接的聚类，对离群点的处理稳健，聚类结果无模式混交现象。同时，算法具有良好的伸缩性，其聚类思想不仅适用于点目标，以可扩展至线、面目标的聚集模式识别，依赖于线、面Voronoi图的生成，根据目标形状特征构建聚集性强度测算方法以实现聚类。

PCVD算法的自适应性取决于聚集目标的空间分布：当聚集目标之间密度近似时，距离函数阈值取均值则可以自动识别目标簇； 但当聚集目标之间密度差异较大时，则需要主动定义常数C的取值以调节得到满意的聚类粒度，这一过程降低了算法的自适应性。常数C取值的变化是聚类粒度在不同聚类层次之间的体现，如何让算法能够自动识别C的取值，实现多尺度的聚类是后续研究中亟待讨论和解决的问题。

参考文献：

[1]ESTIVILLCASTRO V， LEE I. Argument free clustering for large spatial pointdata sets via boundary extraction from Delaunay diagram[J]. Computers， Environment and Urban Systems， 2002， 26（4）： 315-334.

[2]MACQUEEN J. Some methods for classification and analysis of multivariate observations[C]// Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability. Chicago： University of Chicago Press， 1967， 1： 281-297.

[3]KAUFMAN L， ROUSSEEUW P J. Finding Groups in Data： an Introduction to Cluster Analysis[M]. New York： John Wiley & Sons， 1990：38-42.

[4]RAYMOND T N， HAN J W. Efficient and effective clustering methods for spatial data mining[C]// Proceedings of the 20th International Conference on Very Large Data Bases. San Francisco， CA： Morgan Kaufmann Publishers， 1994： 144-155.

[5]ESTER M， KRIEGEL H P， XU X. Knowledge discovery in large spatial databases： Focusing techniques for efficient class identification [C]// Proceedings of the 4th International Symposium on Large Spatial Databases. Berlin： SpringerVerlag， 1995： 67-82.

[6]ZHANG T， RAMAKRISHNAN R， LIVNY M. BIRCH： an efficient data clustering method for very large databases[C]// Proceedings of the 1996 ACM SIGMOD International Conference on Management of Data. New York： ACM， 1996： 103-114.

[7]GUHA S， RASTOGI R， SHIM K. CURE： an efficient clustering algorithm for large databases[C]// Proceedings of the 1998 ACMSIGMOD International Conference on Management of Data. New York： ACM， 1998： 73-84.

[8]GUHA S， RASTOGI R， SHIM K. ROCK： A robust clustering algorithm for categorical attributes[C]// Proceedings of the 15th International Conference on Data Engineering. Washington， DC： IEEE Computer Society， 1999： 512-521.

[9]DASH M， LIU H， SCHEUERMANN P， et al. Fast hierarchical clustering and its validation[J]. Data & Knowledge Engineering， 2003， 44（1）： 109-138.

[10]HANDL J， KNOWLES J， DORIGO M. Antbased clustering and topographic mapping[J]. Artificial Life， 2006， 12（1）： 35-61.

[11]LUMER E D， FAIETA B. Diversity and adaptation in populations of clustering ants[C]// Proceedings of the 3rd International Conference on Simulation of Adaptive Behavior： from Animals to Animats 3. Cambridge： MIT Press， 1994， 1：501-508.

[12]MONMARCH N， SLIMANE M， VENTURINI G. On improving Clustering in Numerical Databases with Artificial Ants[M]. Berlin： Springer， 1999： 626-635.

[13]YANG Y， KAMEL M S. An aggregated clustering approach using multiant colonies algorithms [J]. Pattern Recognition， 2006， 39（7）：1278-1289.

[14]TAN S C， TING K M， TENG S W. A general stochastic clustering method for automatic cluster discovery[J]. Pattern Recognition， 2011， 44（10）： 2786-2799.

[15]CARPENTER G A， and GROSSBERG S. ART2： selforganization of stable category recognition codes for analog input patterns [J]. Applied Optics， 1987， 26（23）： 4919-4930.

[16]KOHONEN T. SelfOrganization and Associative Memory [M]. Berlin： SpringerVerlag， 1989： 119-157.

[17]余莉， 李佳田， 李佳，等. 二维空间聚类的树ART2模型[J]. 计算机应用， 2011， 31（5）： 1328-1330. （YU L， LI J T， LI J， et al. TreeART2 model for clustering spatial data in twodimensional space[J]. Journal of Computer Applications， 2011， 31（5）： 1328-1330.）

[18]HSU A L， HALGAMUGE S K. Enhancement of topology preservation and hierarchical dynamic selforganising maps for data visualization [J]. International Journal of Approximate Reasoning， 2003， 32（2/3）：259-279.

[19]王莉， 王正欧. TGSOM：一种用于数据聚类的动态自组织映射神经网络[J]. 电子与信息学报， 2003， 25（3）： 313-319. （WANG L， WANG Z O. TGSOM： a new dynamic selforganizing maps for data clustering[J]. Journal of Electronics and Information Technology， 2003， 25（3）： 313-319.）

[20]HINNEBURG A， KEIM D A. An efficient approach to clustering in large multimedia databases with noise[C]// Proceedings of the 4th International Conference on Knowledge Discovery and Data Mining. Berlin： SpringerVerlag， 1998， 98： 58-65.

[21]淦文燕， 李德毅， 王建民. 一种基于数据场的层次聚类方法[J]. 电子学报， 2006， 34（2）： 258-262. （GAN W Y， LI D Y， WANG J M. A hierarchical clustering method based on data fields [J]. Acta Electronica Sinica， 2006， 34（2）： 258-262.）

[22]NOSOVSKIY G V， LIU D， SOURINA O. Automatic clustering and boundary detection algorithm based on adaptive influence function[J]. Pattern Recognition， 2008， 41（9）： 2757-2776.

[23]邓敏， 彭东亮， 刘启亮，等. 一种基于场论的层次空间聚类算法[J]. 武汉大学学报（信息科学版）， 2011， 36（7）： 847-852. （DENG M， PENG D L， LIU Q L， et al. A hierarchical spatial clustering algorithm based on field theory [J]. Geomatics and Information Science of Wuhan University， 2011， 36（7）： 847-852.）

[24]ESTIVILLCASTRO V， LEE I. AMOEBA： hierarchical clustering based on spatial proximity using Delaunay diagram[C]// Proceedings of the 9th International Symposium on Spatial Data Handling. Berlin： SpringerVerlag， 2000， 26-41.

[25]ESTIVILLCASTRO V， LEE I. Multilevel clustering and its visualization for exploratory data analysis[J]. GeoInformatica， 2002， 6（2）： 123-152.

[26]LIU D， NOSOVSKIY G V， SOURINA O. Effective clustering and boundary detection algorithm based on Delaunay triangulation[J]. Pattern Recognition Letters， 2008， 29（9）： 1261-1273.

[27]ESTER M， KRIEGEL H P， SANDER J， et al. A densitybased algorithm for discovering clusters in large spatial databases with noise[C]// Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining. Menlo Park， California： AAAI Press， 1996： 226-231.

[28]PARKER J K， DOWNS J A. Footprint generation using fuzzyneighborhood clustering[J]. GeoInformatica， 2013， 17（2）： 285-299.

[29]武佳薇， 李雄飞， 孙涛，等. 邻域平衡密度聚类算法[J]. 计算机研究与发展， 2010， 47（6）： 1044-1052. （WU J W， LI X F， SUN T， et al. A densitybased clustering algorithm concerning neighborhood balance [J]. Journal of Computer Research and Development， 2010， 47（6）： 1044-1052.）

[30]WANG W， YANG J， MUNTZ R. STING： a statistical information grid approach to spatial data mining[C]// Proceedings of the 23rd International Conference on Very Large Databases. San Francisco， CA： Morgan Kaufmann Publishers Inc， 1997： 186-195.

[31]AGRAWAL R， GEHRKE J， GUNOPULOS D， et al. Automatic subspace clustering of high dimensional data[J]. Data Mining and Knowledge Discovery， 2005， 11（1）： 5-33.

[32]GOLD C M. Problems with handling spatial data— the Voronoi approach[J]. CISM Journal， 1991，45（1）： 65-80.

[33]陈军， 赵仁亮. Voronoi动态空间数据模型[M]. 北京： 测绘出版社， 2002： 24-47. （CHEN J， ZHAO R L. Voronoi Dynamic Spatial Data Model[M]. Beijing： Surveying and Mapping Press， 2002： 24-47.）