授之以鱼,不如授之以渔
2016-05-14黄小蓉
黄小蓉
中图分类号:G623.5 文献标识码:A 文章编号:1002-7661(2016)05-0039-02
新课标指出:“课程内容要反映社会的需要、数学的特点,要符合学生的认知规律。它不仅包括数学的结果,也包括数学结果的形成过程和蕴含的数学思想和方法。”这就意味着我们不能只教授数学知识的结果,而应该使学生体验数学知识的形成过程,感悟到其中蕴含的数学思想和方法,所谓“授之以鱼,不如授之以渔”。那怎么才能很好的做到呢?笔者想通过自己上过的《植树问题》一课,重点谈谈在符合学生认知规律的基础上是怎么充分挖掘知识结果中蕴含的数学思想方法,使掌握数学知识的结果、体验知识的形成及感悟数学思想方法有机结合。
[课堂实录]
(一)游戏铺垫
拍手游戏:“青蛙跳水歌”。这个游戏中你觉得有什么数学思想吗?
其实这首儿歌里蕴涵了“一一对应”的数学思想,一只青蛙和一张嘴对应,一只青蛙和两只眼睛对应,一只青蛙还和什么对应?
“一一对应”的思想是非常重要的数学思想,在我们生活中经常用到,比如说吃饭时,一个碗和一双筷子对应,你还能举些这样一一对应的例子吗?
(设计意图:上课伊始,就在轻松活泼愉悦的游戏中渗透本节课要运用的“一一对应”思想,为新课的理解打下了伏笔。)
(二)观察导课
我们再来观察一下手,你发现了哪些数?(5,4)两个手指之间的空隔,在数学上叫做“间隔”。像这样的间隔在生活中随处可见,请看图片。你能说说你身边的间隔吗?
今天我们就来研究跟间隔有关的“植树问题”。
(设计意图:在人人都有的、最常用的“手”中观察并理解什么叫“间隔”,并举例说说身边的间隔,让学生感受到生活中、甚至人体自身上都有数学,数学并不遥远和神秘。)
(三)出示例题
招聘启事
学校将对校园进一步绿化,特聘校园设计师一名,要求在一条40米的小路一边植树,每隔10米栽一棵,请设计方案一份,画出线段图,择优录取。
师:从中你发现了哪些数学信息?(小路的总长度叫“总长”,树与树之间每个间隔的距离叫“间距”。)
(设计意图:通过一则招聘启事这个具体情境出示例题,既使学生感受到运用数学问题是社会生活的需要,也使学生对校园建设充满了主人翁意识。)
(四)指导画图
为什么平均分成4段或者说4个间隔?怎么计算?(40x00=4(棵))
你可以在这条线段图上画几棵树呢?开始设计吧,并列式计算。
(五)设计交流
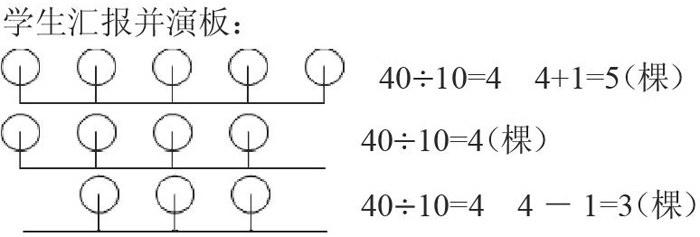
学生汇报并演板:
(六)猜想规律
这三种方案从线段图来看,有什么异同?
同:总长相等,都是40米;间距相等,都是10米;中间都栽了3棵树……
异:两端都栽只栽一端两端不栽
从算式来看呢?
同:都要先算出“间隔数”,用“总长)c间距一间隔数”
异:两端都栽,“间隔数+1=棵数”
只栽一端,“间隔数一棵数”
两端不栽,“间隔数-1=棵数”
(七)探索验证
这三种栽法间隔数和棵数的规律是不是普遍存在呢?你想怎么验证一下吗?
(1)列举法:分组在草稿纸上画线段图,第一组画两端都栽,第二组画只栽一端,第三组画两端不栽,任意画几个间隔,看你画几棵树。(汇报填表,验证规律。)
(2)对应法:可以用“一一对应”的思想来说明:一个间隔一棵树,一个间隔又一棵,……(课件演示,验证规律。)
(3)手势法:其实我们的手早已经给我们验证这些规律,不信,伸出手试试看。(课件展示,验证规律。)
(八)运用规律
做书P117例题1、P118例题2及其“做一做”3道题。
做例题1、2时要学生说:题中有什么重要信息,要求的是什么?
“做一做”的题目,让学生独立试着做,汇报时有错误的让学生自己互相评价指正。
(九)全课小结
[实践反思]
1.将数学方法与思想巧妙结合,揭示背后的思想
很多时候,老师们只注重传授解题的方法,而忽略了方法背后用于支撑方法的思想,学生只知其然,不知其所以然,只知机械地模仿解题,不知为何如此解题,只知老师教一点就学一点,不知自己去探索未知,所以我一改常态,不但让学生自己去发现规律,更着重让学生通过列举法、对应法、手势法去领悟规律背后的“一一对应”思想。
2.将数学与游戏、肢体、生活紧密结合,感受数学的快乐
上课伊始,在活泼有趣的拍手游戏中,让学生初步地感受到“一一对应”思想,为新课做好铺垫;接着,通过观察手,让学生感悟到原来我们的肢体中也有数学,认识了什么叫“间隔”,初步体验到个数与间隔数之间的关系;然后,让学生说生活中的“间隔”及看招聘启事中的事例,让学生了解到数学并不遥远、神秘和深奥,而是那样的接近、有用和快乐。
3.将操作和交流、猜想和探索有机结合,体现学生的主体
我一贯坚持一个原则:学生能自己做的,老师绝不包办,学生有困难时,老师才给予点拨。所以,我放手让学生通过画图设计植树方案,这样三种情况全出现了,而这正是我所需要的,不拘泥于只讲其中一种情况。再通过将三种情况的异同点进行对比,让学生提出普遍规律的猜想,然后寻求验证,学生想到了三种方法:列举法、对应法和手势法,从中揭示了虽然三种情况的规律各有不同,但它们都具有统一的数学思想——“一一对应”,让学生有了深刻地理解和记忆。在操作和交流、猜想和探索中,学生体验了知识形成的全过程,体现了学习主体性地位。
总之,这节课充分挖掘了知识结果中蕴含的数学思想,使学生不但掌握了数学知识、体验了知识形成的过程,而且还感悟了其中的数学思想,做到了“既授之以鱼,又授之以渔”。
(责任编辑 曾卉)