非完全图TSP问题研究
2016-05-14张家善
张家善

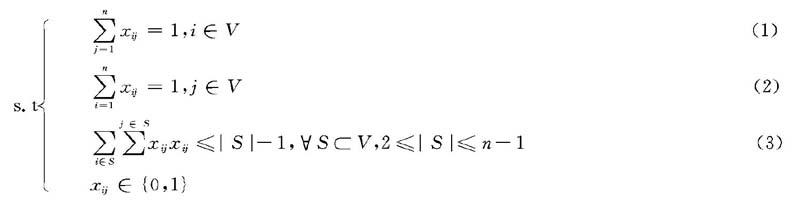
摘要:指出了TSP问题是一种具有代表性的组合优化问题,在现实生活中有着广泛的应用。不同于完全图,非完全图TSP问题中存在着某些节点之间没有路径直接相连,使得处于该节点位置时,其路径选择受到一定限制。受运筹学中大M法思想的启发,提出了通过引入一个非常大的正数(即大M)来表示此类节点间的距离,从而将非完全图TSP问题转化成完全图TSP问题,降低了问题求解的难度,并且验证了该方法的有效性。
关键词:TSP问题;非完全图;大M法;仿真
中图分类号:F57
文献标识码:A 文章编号:1674-9944(2016)05-0182-02
1 引言
旅行商问题(Traveling Salesman Problem,TSP),又称货郎担问题或旅行推销员问题,最早由美国的Rand公司提出。问题可简单描述为: 设有n个城市(节点),若从某城市(节点)出发,遍历各城市(节点)一次后返回原出发点,要求找出一条路线,使总路径最短[1]。TSP问题的图论描述为:设图G=(V,E), V代表顶点集,E代表由不同顶点组成的边集,已知道各边的长度dij,要找出一个Hamilton回路,使它的距离最短。现实生活中有很多问题可以归结为旅行商问题,比如邮路问题、连锁店的货物配送路线问题、装配线上的螺帽问题和产品的生产安排问题等[2],其研究具有重要的理论意义和应用价值。
通过中国知网检索发现,国内外学者就TSP问题进行了相关研究:Pintea等人[3]将蚁群优化算法应用于解决旅行商问题;李勇采用动态蚁群算法研究了TSP问题[4];李如琦提出用MAX_MIN蚂蚁算法解决中国旅行商问题[5];国圆媛应用蚁群算法解决了浙江旅行商问题的最短路径[6];潘庆祥建立了有向图TSP模型,并设计了算法进行求解[7]。
2 TSP问题分类
按照TSP路径关系的不同特征,通常有以下两种基本分类。
(1)根据任意两个城市(节点)之间是否均存在路径(边)相连接,可分为完全图TSP问题 与非完全图问题。完全图是指一个图的每一对不同顶点恰有一条边相连,基于完全图的旅行商问题即为完全图TSP问题;非完全图是指存在两个顶点之间没有边相连接,即n个端点的连接边数少于n(n-1)/2条边,基于非完全图的旅行商问题 即为非完全图TSP问题。
(2)根据任意两个城市之间来回路径均是否相等,可分为无向图TSP问题和有向图TSP问题。所谓无向图,是指一个图中的每条边都没有方向,往返的费用值相等,即dij=dji;所谓有向图,是指一个图中的每条边有方向,往返的费用值不等,即dij≠dji
上述研究多是针对完全图TSP问题,而完全图是一种简单图,任何两个顶点之间均有线路连接,处于当前节点时,可以选择任意节点作为待访问的后续节点,问题求解相对容易。但是,针对非完全图的研究较少。
3 非完全图TSP问题的数学模型
与完全图TSP问题不同, 非完全图TSP问题中存在城市之间没有路径连接,需要对问题进行转换处理。一种设想是寻找一条经过第三个城市的最短路来间接地表示两个城市之间的路径关系[8],即令
上式中,n为集合中所含图的顶点数。约束(1)和(2)意味着对每个点而言,仅有一条边进和一条边出;约束(3)则保证了没有任何子回路解的产生。于是,满足约束(1)、(2)和(3)的解构成了一条Hamilton回路。
4 实例验证
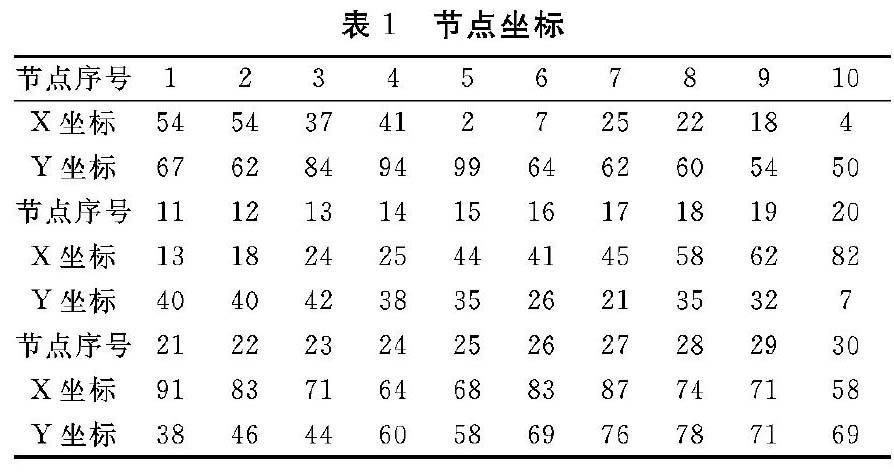
选取oliver30问题作为研究对象(节点坐标如表1所示),随机选取节点17与20,22与26,28与4三对节点,设置其间没有边连接,将其改造成非完全图TSP问题,如表1所示。根据前文所述,设置节点对17与20,22与26,28与4之间的距离d17.20,d22.26,d4.2S为M,考虑本例节点间距,取M=10000。
采用蚁群算法在计算机上仿真计算,得到最优路径如图1所示。
在非完全图TSP问题中,搜索TSP路线的次数应等于或者少于完全图TSP问题,所得到的TSP路线方案总数也应少于完全图TSP情形。本例中,由于节点17与20没有路径直接相连接(可认为距离值非常大),如图中虚线所示,只能途径18,19号节点再到达20号节点。同样,节点22与26,28与4之间,只能途径其他节点绕道抵达。仿真计算得到最短路径为:
20→ 21→22→23→25→24→26→27→28→29→30→ 2→ 1→ 3→ 4→ 5→ 6→ 7→ 8→ 9→10→11→12→13→14→15→16→17→18→19。
对应的路径距离值:423.7406。
5 结语
非完全图TSP问题中存在着某些城市(节点)之间没有路径直接相连,使得处于该节点位置时,其路径选择受到一定限制,这给问题的解决带来了一些困难。受到运筹学中大M法思想的启发,通过引入一个非常大的正数(即大M)来表示这些节点间的距离,从而将非完全图TSP问题转化成完全图TSP问题,降低了问题求解的难度,使其变成规范化的、易于求解的TSP问题。需要指出的是,本文提出的这种将非完全图TSP问题转化成完全图TSP问题的转化思想,同样适用于其他非标准TSP问题。
参考文献:
[1]余详宣,崔国华.计算机算法基础[M] .武汉:华中科技大学,1998.
[2]李会玲.基于模拟退火的遗传优化算法在TSP问题中的应用[J].热处理技术与装备,2007,28(6):51~55.
[3]Pintea C M,Pop P C,Dumitrescu D.An ant-based technique for the dynamic generalized traveling salesman problem[C].Proceedings of the 7th WSEAS International Conference on Systems Theory and Scientific Computation,2007:257~261
[4]李 男,段正澄.动态蚁群算法求解TSP问题[J].计算机工程与应用,2003,39(17):104~107.
[5]李如琦,苏媛媛.用MAX_MIN蚂蚁算法解决中国旅行商问题[J].湖南工业大学学报,2007(5)
[6]国圆媛,许延鑫,吴 江.浙江旅行商问题研究[J].中国新技术新产品,2009(22):147~149.
[7]潘庆祥,徐自然.具有重复路径的有向TSP问题[J].才智,2014(17):103~106.
[8]徐心和.旅行商问题的一种新解法[J].东北工学院学报,1990,1(1):68~74.
